The Expansion of a Wedge of Gas into Vacuum with Small Angle in Two-Dimensional Isothermal Flow∗
Ju GE Wancheng SHENG
1 Introduction
In this paper,we consider the two-dimensional is entropic compressible Euler equations

where(u,v)and ρ denote the velocity and the density,respectively,while the pressure p is given by p(ρ)= ρ for the isothermal case.For the Riemann initial data,we may seek the self-similar solutions(u,v,ρ)=(u,v,ρ)(ξ,η)for the reason that(1.1)and the Riemann initial data are invariant under the stretch(x,y,t)→(kx,ky,kt)(k>0).This kind of initial value problem is called the two-dimensional Riemann problem.The Riemann problem in general is very complicated.A simpler situation is the expansion problem of a wedge of gas into vacuum.
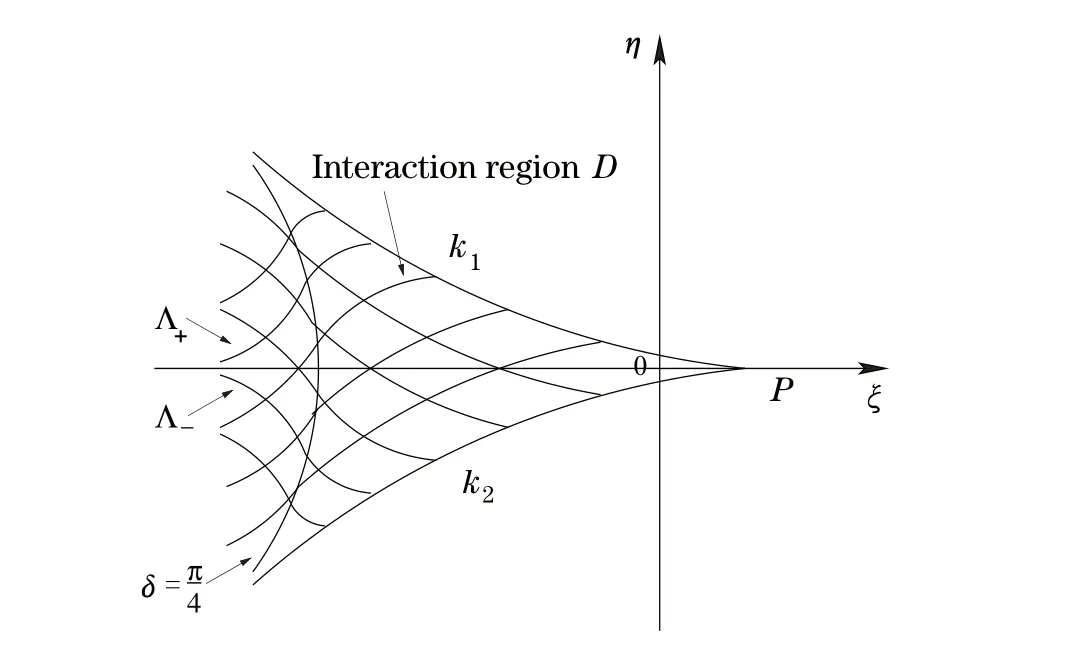
This problem has been an interesting problem for a long time.In[6],Dai and Zhang used the characteristic decomposition method to establish the global smooth solution for the expansion problem of the pressure gradient system.In[14],by the hodograph transformation and the characteristic decompositions of characteristic angles,Li and Zheng obtained various priori estimates and constructed classical self-similar solutions to the interaction of two planar rarefaction waves for the two-dimensional polytropic Euler equations.In[12],Li,Yang and Zheng developed the direct approach to recover all the properties of the solutions obtained by the hodograph transformation of Li and Zheng[14].They obtained the existence of the solution for< θ In this paper,we prove the global existence of the solution to the expansion problem of a wedge of gas into vacuum to the two-dimensional isothermal Euler equations by the direct method in the case 0< θ ≤,where θ is the half angle of the wedge.Our research relies on the bootstrapping argument and the analysis of α,β instead of c for the reason that c=1 for the isothermal flow.This paper is organized as follows.In Section 2,we give some preliminaries,including the characteristic forms of the isothermal Euler equations and some characteristic decompositions of the inclination angle(α,β).In Section 3,the expansion problem of a wedge of gas into vacuum is considered,and the main results are obtained. Here is a list of our notations: Consider the two-dimensional isentropic isothermal compressible Euler equations(1.1).For the smooth self-similar solutions,the system(1.1)can be written as where(U,V)=(u−ξ,v−η)is the pseudo-velocity,and q=lnρ for ρ>0.The eigenvalues of(2.1)are The curvesare the(pseudo-) flow characteristics and the(pseudo-)wave characteristics of(2.1),respectively. We further assume that the flow is ir-rotational,i.e.,uη=vξ.Then(2.1)can be rewritten as supplemented by Bernoulli’s law(see[13]): The characteristic forms of the system are ∂±u+ Λ∓∂±v=0.As in[14]and[12],let α and β be the inclination angle variables of wave characteristics,that is, Then,for the convenience of solving the gas expansion problem,we choose Then,using(2.6),we get Then,we have In addition,we cite the following commutator relation offrom[12–13]and the characteristic decompositions in[7]. Lemma 2.1 (Commutator Relation of)For any C2smooth function I(ξ,η),there holds Lemma 2.2 For the inclination angles α and β,we have where Lemma 2.3 For the inclination angle σ of Λ0-characteristics,we have where and IntroduceThen,we have a(δ)>0 if δ> θ. Lemma 2.4 For the inclination angles α and β (α − β ?=,π),we have where In this section,by the characteristic decompositions in the previous section,we discuss the expansion problem of a wedge of gas into vacuum directly in the(ξ,η)plane. For convenience,we place the wedge of gas symmetrically with respect to the x-axis and the sharp corner at the origin,as in Figure 3.1(a).Let θ∈ ?0,?be the wedge half-angle and l1,l2denote the two edges of the wedge.At the time t=0,the wedge is full of the gas,and vacuum is outside.Then the gas would expand into the vacuum.This problem is then formulated mathematically as seeking the solution of(2.3)with the initial data where ρ0>0 is a constant,and ω =arctanis the polar angle.In fact,this problem can be considered as a two-dimensional Riemann problem of(2.3)with two pieces of initial data(3.1).Through the analysis in the above subsection,the gas away from the wedge expands uniformly to infinity as planar rarefaction waves R1and R2which satisfy Figure 3.1 The expansion of a wedge of gas whereζ=n1ξ+n2η,with(n1,n2)=(sinθ,−cosθ)and(n1,n2)=(sinθ,cosθ),respectively(see Figure 3.1(b)).Then the rarefaction wavesR1andR2emitting from the initial discontinuitiesl1andl2begin to interact atin the(ξ,η)plane.The wave interaction regionDis formed adjacent to the planar rarefaction waves with boundariesk1andk2(see[7]). Gas Expansion Problem Find a solution of(2.3)and(3.1)inside the wave interaction regionD,subject to the boundary values onk1andk2,which are determined continuously from the rarefaction wavesR1andR2. The equations(2.8)can be reduced to a diagonal form Letandis betweenθand mDax{δ})be the region enclosed by the three curvesk1,k2andξ=(see Figure 3.2).Then,for the boundary data Figure 3.2 The domain Dδ we get the following result as Lemma 5.2 in[7]. Theorem 3.1 (Local Existence)There is a δ0>0 such that the C1solution of(3.3)and(3.4)exists uniquely in the region Dδ0,where δ0depends only on the C0and C1norm of α,β on the boundaries k1and k2. Lemma 3.1 (Boundary Data Estimates(see[7]))If 0< θ≤ θ,there holds Lemma 3.2 Assuming that the solution(α,β)∈ C1,we have thatare positive and bounded in Here we note thatwhich can be obtained by(2.8). Proof By(3.4),we getα =0 andβ =0 on k1and k2,respectively.So,we obtain thaton k1and k2,respectively.Using the characteristic decompositions(2.12),we get Next,we prove thatSuppose that ξ=ξδ1is the first time thaWithout loss of generality,we assume thatat the point P1on the line ξ= ξδ1.From the first equation of(2.12),we have Note that the direction ofis the direction fromto the boundary.Thus,we have at point P1.It leads to a contradiction.Then,we have Introducing new variables m1= α −and m2= −β −,we get where Then,we have the results as follows. Lemma 3.3 If 0< θ≤|m1|≤ M and|m2|≤ M,then F(m1,m2)and G(m1,m2)are positive and bounded in Dδ. Proof Because|m1|≤ M,|m2|≤ M,we have Then,we haveFrom Lemma 3.2,considering the fact that sinx and x are equivalent in finitely small,we get our result in this lemma. Theorem 3.2 Assuming that there is a C1solution in Dδ,0< θ≤,then we have Moreover,the above inequalities must be strict in the interior of Dδ,that is, Proof Considering M=−θ,then,we have that proving the inequalities(3.12)is equivalent to proving|m1| From(3.4),through the characteristic decompositions,we have that there exists a neighborhood ω1of k1such that|m2| We select a Λ−characteristic curve?k1in ω1and a Λ+characteristic curvein ω2,taking them as the new boundaries and the data on them as the initial data in the bootstrapping argument. Next,we would prove|m1| and solving the equation along C1from P0to P1,we get In view ofds and Lemma 3.3 and the choice condition of P1,we have Similarly,utilizing the second equation of(3.8),we get|m2(ξ1,η1)| From Theorem 3.2,we have θ< δ≤−θ.Considering(3.7),we can get that X=C(θ,γ)is a constant independent ofBy(2.7)–(2.8),the gradient estimates can be obtained by Lemma 3.2 directly,similar to[7]. Lemma 3.4β are all uniformly bounded for the C1solution in Dδ. Lemma 3.5 Assume that there is a C1solution in,where the system is hyperbolic(α − β ?=0,π).Then the C1norm of α,β,u,v have a uniform bound C=C(θ,γ): Theorem 3.3 (C1,1Estimates)Assume that there exists a smooth solution in the domain Dδ.Then,there exists a constant C(θ,γ),such that ProofFrom Lemma 3.5 and(3.16),it suffices to prove thatFrom the first equation in(2.10)and(3.16),we geteasily.By the commutator relation(2.9),we get Using(2.9)for I=α,we get From(2.8)–(2.10)and(3.18),we get a first-order equation of Figure 3.3 Convexity types of characteristics as 0<θ≤θ where P and Q are algebraic functions of α,β,?α.Integrating(3.20)along the directionand considering(3.16),we get thatα| Through the prior estimates,we could extend the local solution to the global smooth solution. Theorem 3.4 (Global Existence) There exists a unique global smooth solution to the interaction of two rarefaction waves with the interaction(half)angle θ ∈ (0,.As shown in Figure 3.3,the Λ±characteristics are concave and convex,respectively,before they hit the curve δ=and the Λ±characteristics are convex and concave,respectively,after they cross the curve δ= ProofThe proof follows from the previous results,including Theorems 3.1–3.3 and the fact that the curve ξ= ξδis non-characteristic.Here,we omit the details since they are similar to those in[6,14].Differentiating(2.5),we get By Lemma 3.2,we get the convexity types immediately. Remark 3.1 The global existence of the solution to the expansion problem of the isothermal Euler equations for 0<θ [1]Chang,T.,Chen,G.Q.and Yang,S.,On the 2-D Riemann problem for the compressible Euler equations I,Interaction of shocks and rarefaction waves,Discrete and Continuous Dynamical Systems,1(4),1995,555–584. [2]Chang,T.,Chen,G.Q.and Yang,S.,On the 2-D Riemann problem for the compressible Euler equations II,Interaction of contact discontinuities,Discrete and Continuous Dynamical Systems,6(2),2000,419–430. [3]Chang,T.and Hsiao,L.,The Riemann problem and interaction of waves in gas dynamics,Pitman Monographs,Longman Scientific and Technical,Essex.,41,1989,95–161. [4]Chen,X.and Zheng,Y.X.,The interaction of rarefaction waves of the two-dimensional Euler equations,Indiana Univ.Math.J.,59,2010,231–256. [5]Courant,R.and Friedrichs,K.O.,Supersonic Flow and Shock Waves,New York,Interscience,1948. [6]Dai,Z.H.and Zhang,T.,Existence of a global smooth solution for a degenerate Goursat problem of gas dynamics,Arch.Ration.Mech.Anal.,155,2000,277–298. [7]Hu,Y.B.,Li,J.Q.and Sheng,W.C.,Goursat-type boundary value problems arising from the study of two-dimensional isothermal Euler equations,Z.angew Math.Phys.,63,2012,1021–1046. [8]Hu,Y.B.and Sheng,W.C.,Characteristic decomposition of the 2×2 quasilinear strictly hyperbolic systems,Appl.Math.Lett.,25,2012,262–267. [9]Levine,L.E.,The expansion of a wedge of gas into a vacuum,Proc.Camb.Philol.Soc.,64,1968,1151–1163. [10]Li,J.Q.,On the two-dimensional gas expansion for compressible Euler equations,SIAM J.Appl.Math.,62(3),2001/2002,831–852. [11]Li,J.Q.,Global solution of an initial-value problem for two-dimesional compressible Euler equations,J.Differential Equations,179(1),2002,178–194. [12]Li,J.Q.,Yang,Z.C.and Zheng,Y.X.,Characteristic decompositions and interactions of rarefaction waves of 2-D Euler equations,J.Differential Equations,250,2010,782–798. [13]Li,J.Q.,Zhang,T.and Zheng,Y.X.,Simple waves and a characteristic decomposition of the two dimensional compressible Euler equations,Commu.Math.Phys.,267,2006,1–12. [14]Li,J.Q.and Zheng,Y.,Interaction of rarefaction waves of the two-dimensional self-similar Euler equations,Arch.Rational.Mech.Anal.,193,2009,623–657. [15]Suchkov,V.A.,Flow into a vacuum along an oblique wall,J.Appl.Math.Mech.,27,1963,1132–1134. [16]Wang,R.H.and Wu,J.C.,On mixed initial boundary value problem for quasi-linear hyperbolic system of partial differential equations in two independent variables,Acta Sci.Nat.Jilin.Univ.,2,1963,459–502(in Chinese). [17]Zhang,T.and Zheng,Y.X.,Conjecture on the structure of solutions of the Riemann problem for two dimensional gas dynamics systems,SIAM J.Math.Anal.,21,1990,593–630. [18]Zhao,W.X.,The expansion of gas from a wedge with small angle into a vaccum,Comm.Pure Appl.Anal.,12,2013,2319–2330.
2 Preliminaries






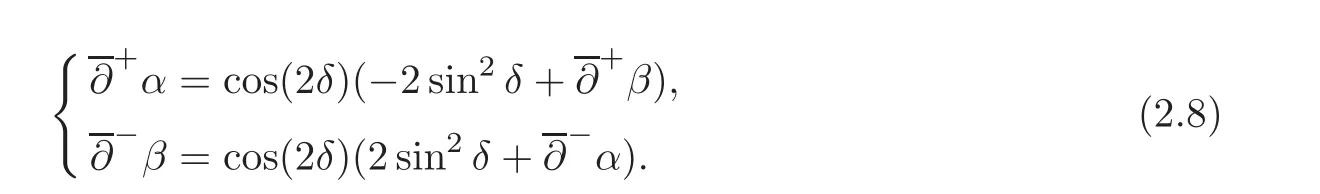
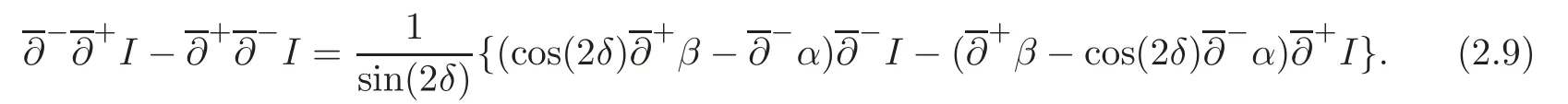
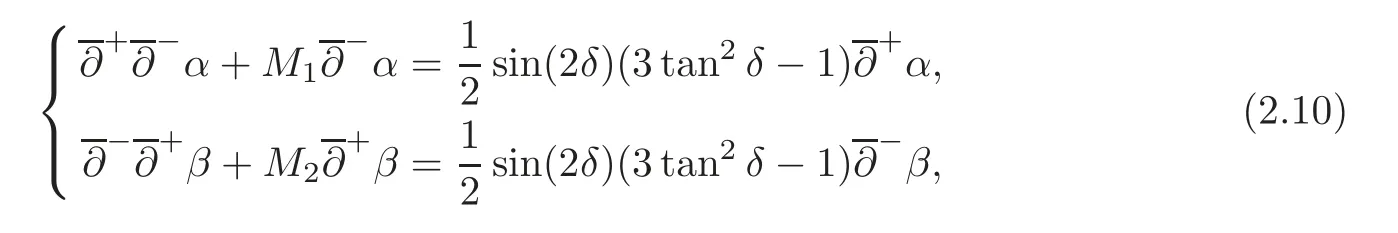
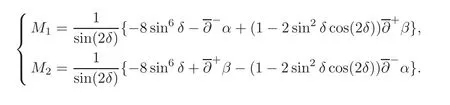
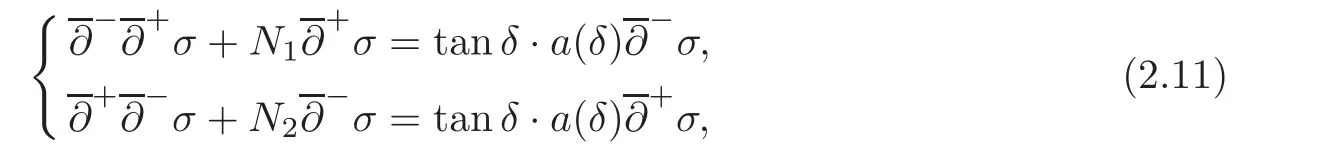


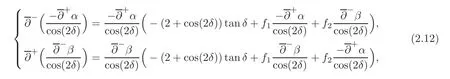
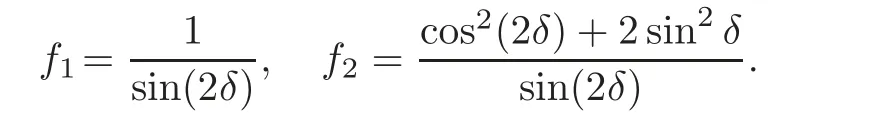
3 The Gas Expansion Problem to the Isothermal Euler Equations for the Case That θ ∈ (0,θ]
3.1 The expansion problem of a wedge of gas into vacuum
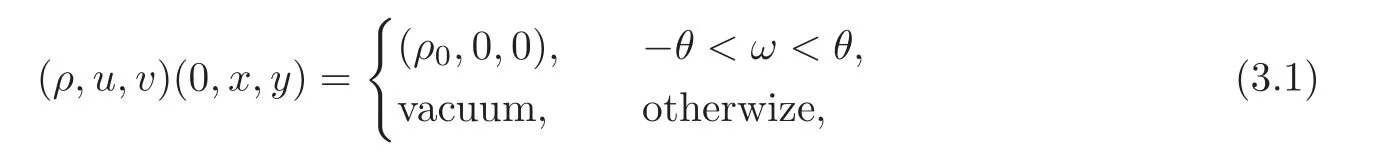

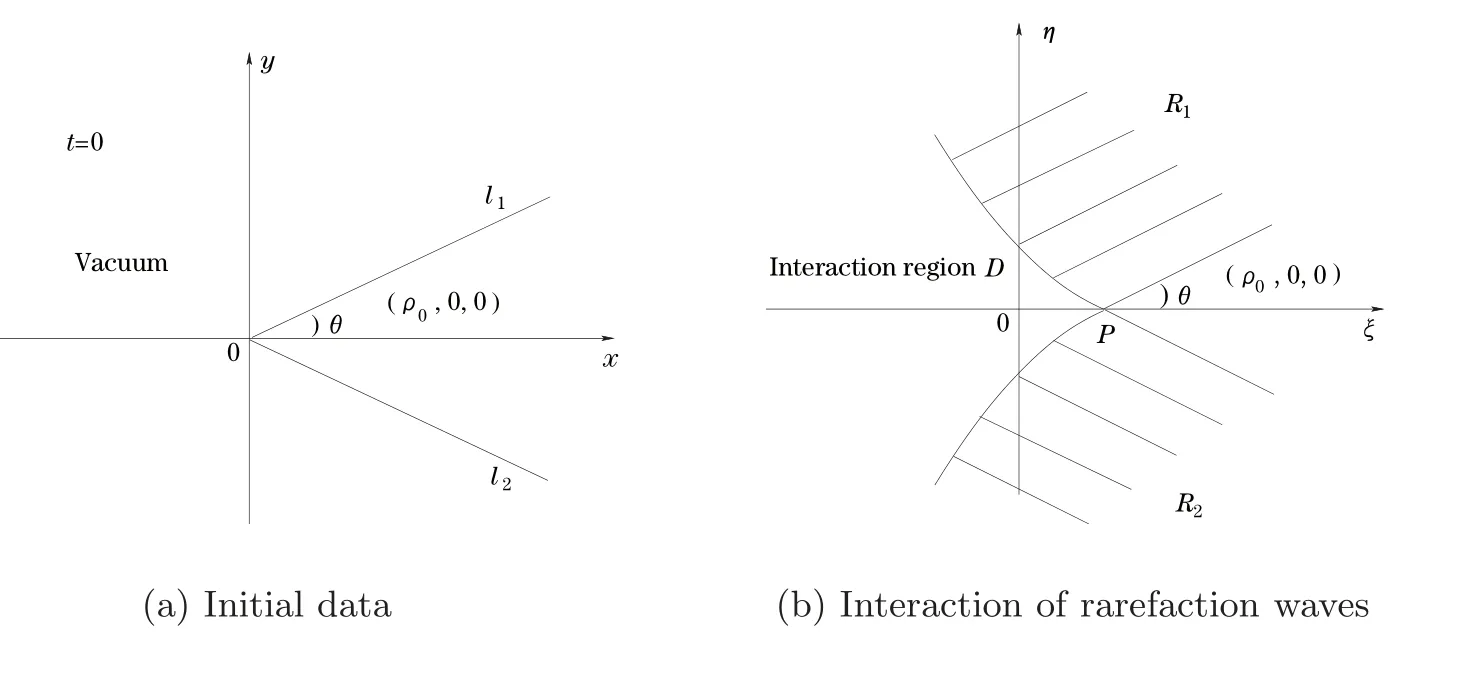
3.2 The existence of local solutions

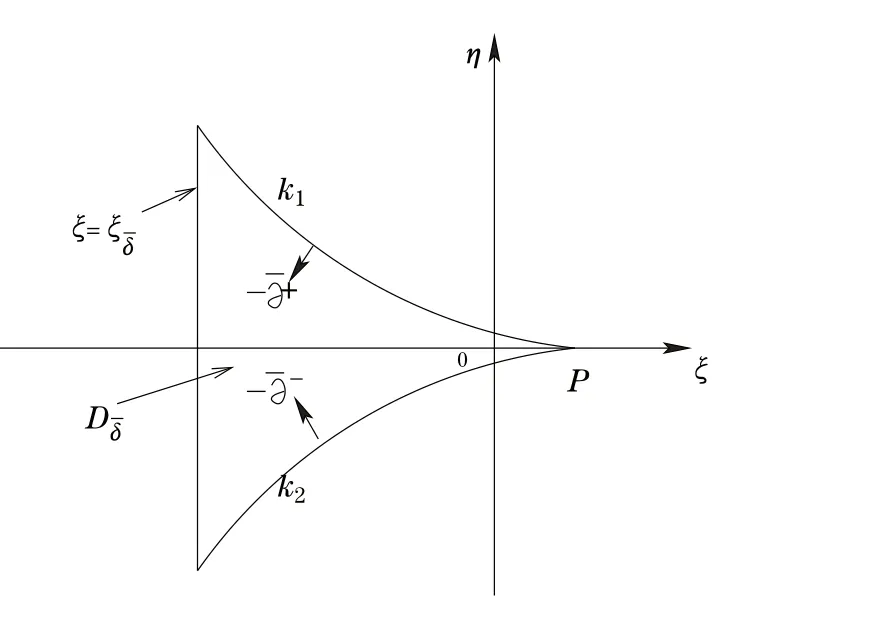

3.3 Estimates for the case that θ ∈ (0,θ]
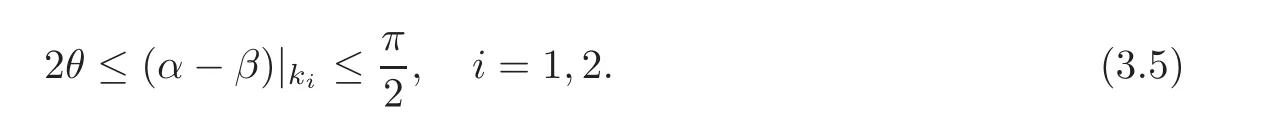

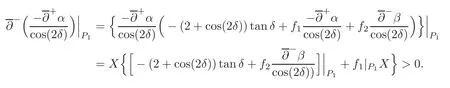
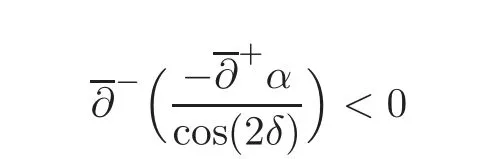

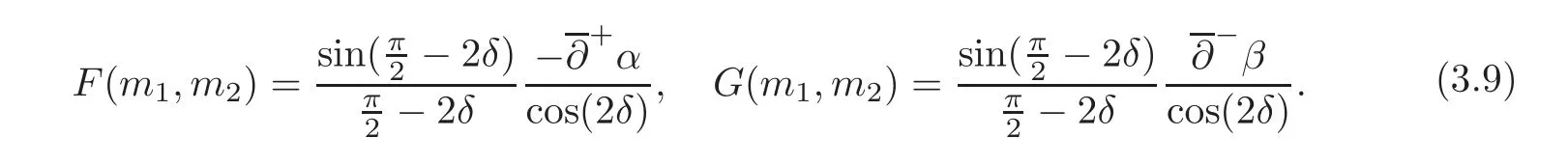

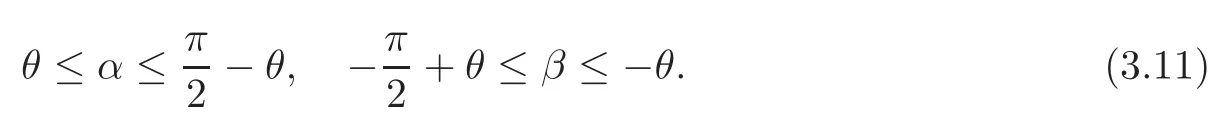
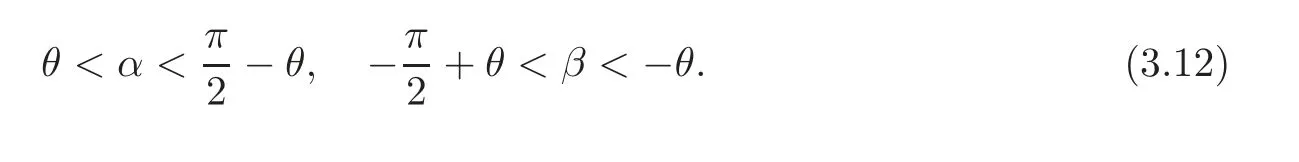





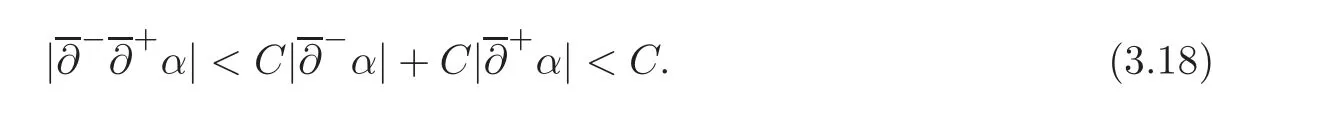
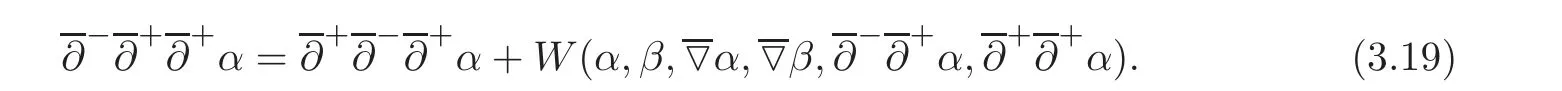

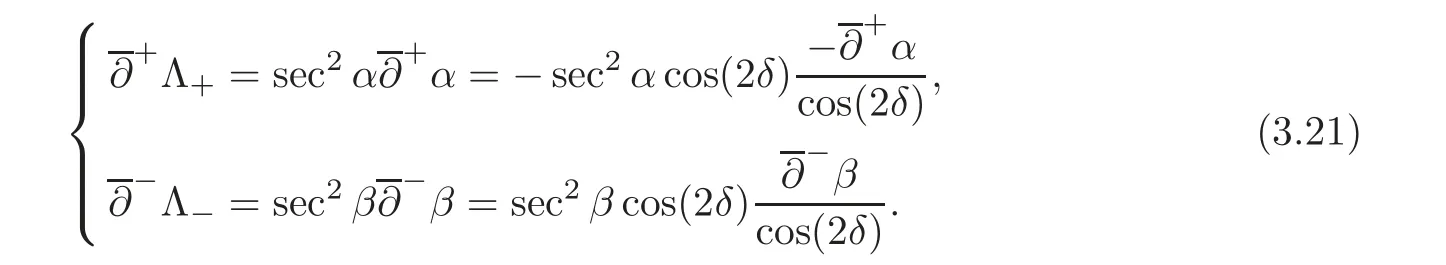
 Chinese Annals of Mathematics,Series B2016年3期
Chinese Annals of Mathematics,Series B2016年3期
