基于误差估计的多传感器异步融合处理

凌翔

【摘 要】为了提高多传感器数据融合中的精度，本文提出了基于误差估计的异步融合处理方法，该方法将传感器观测值与融合航迹的预测值直接融合，同时保证多传感器融合结果的数据率和融合之后的精度。本文进行了对比仿真实验，结果表明该方法在直线和转弯条件下的估计精度都比同步方法更高。

【关键词】异步融合；航迹跟踪；误差概率

【Abstract】To improve the precision of data fusion in multi-sender network， this article proposed an asynchronous fusion method based on error estimation. In this method， the observations of every sensor calculated with fusion tracks directly， assuring data rate and precision simultaneously. In this article， comparison between asynchronous and synchronous methods is made， and indicates that the result of asynchronous method are better than the other one.

【Key words】Asynchronous fusion； Tracking； Error Probability

0 引言

多元传感器融合处理能通过综合多角度、多类传感器的不同观测，实现数据率、精度和发现概率的提高。要实现这些指标的提升，需要对多个传感器的观测值进行综合估计。但是由于不同传感器的数据率可能并不相同，或者即便相同数据率的传感器对同一目标的观测时间也不一样，这就使得数据融合首先要解决数据的时间配准[1]。

数据融合按照时间配准的方法可分为同步融合和异步融合两类。同步融合[2]是将多个传感器的观测值同步到一个时刻，并进行综合参数估计；异步融合[3]并不需要做时间同步，而是直接对每一个观测进行单独的参数估计过程。因此异步融合的数据率通常比同步融合更高，对不同传感器的观测时序不作任何假设或要求。

1 多源数据融合的一般方法

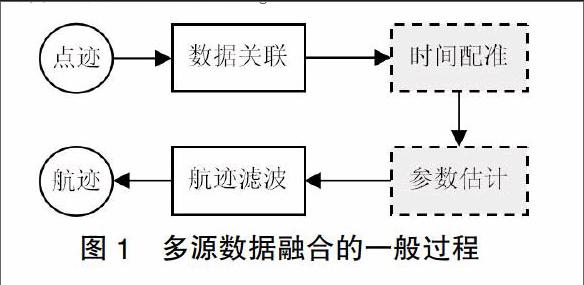
多源传感器的数据融合一般分为三个阶段：配准、参数估计和滤波，而一般单一传感器的目标跟踪不需要配准和参数估计。因此就工程实践来说，多源传感器的目标跟踪与单传感器的跟踪在软件实现步骤上基本一致，只不过多源融合程序增加了时间配准和参数估计的过程。整个的融合过程如图1所示。

1.1 融合架构

信息融合方法从架构上可分为分布式和集中式两种[4，5]。分布式融合[6]是对每一个传感器观测进行独立的跟踪，产生局部航迹，之后对所有的局部航迹进行融合，产生全局航迹。这样做的优点是融合中心得到的信息更多（如速度、加速度等），有利于时间配准中对观测数据在时间维度上的插值和外推；缺点是由于需要对单独传感器进行独立跟踪，因此难以通过增加传感器提高发现概率。

集中式融合将各传感器的原始观测值进行统一融合处理，直接产生全局航迹，这样做的好处是能提高系统整体的发现概率，当单一传感器发现概率达不到系统要求时，通过数据融合使全局发现概率达到检测要求。

1.2 时间配准

为了对多个传感器数据进行融合，必须将多个传感器的数据和融合历史数据配准到同一个时刻，然后才能进行参数估计。时间配准包含两个任务：1.选择合适的时刻；2.对数据进行预测或内插。

一般情况下，选定某一个主传感器的观测时刻为融合时刻，或者使用融合系统自身处理节拍的时刻作为融合时刻，所有其他传感器的数据统一地通过预测或内插调整至融合时刻。这种方法称为同步融合，好处是能够在每一个时刻得到更多的观测数据，从而进行精确的估计；坏处是融合数据率低于传感器的原始数据率，并且更多的传感器无法提高融合数据率，而只能提高精度。

直接对传感器的观测数据进行融合[7]，并在每次收到任何一个传感器观测数据后都将该数据与历史数据做实时融合并给出融合结果。这种方法称为异步融合，好处是更多的传感器可以得到更高的数据率的同时也能提高融合精度，坏处是实时观测数据只能和历史数据进行融合，而非最新的观测数据，从而影响融合精度。

2 基于误差概率的异步融合

本文方法以集中式融合为架构，将多传感器的观测值直接与全局航迹关联和融合，实现全局航迹的实时更新，是一种集中式异步融合方法。

2.1 集中式异步融合处理

集中式异步融合处理是将传感器观测与全局航迹的外推值进行融合，因此每一次融合分为三个步骤：1）全局航迹外推；2）参数估计；3）航迹滤波。

本文使用的航迹滤波方法采用匀加速运动卡尔曼滤波。实际上，基于误差概率的异步融合方法与采用的滤波算法没有关系，更好的、更符合目标运动特征的滤波算法能够得到更好的结果。

2.2 误差概率估计

传感器通常会上报多个维度的观测数据，大部分是以传感器为原点的极坐标。不同类型的传感器其距离和方位误差差别巨大，例如基于电磁波的传统雷达通常距离精度高，方位精度差；而基于可见光的激光雷达距离精度很差，但方位精度极高。可以对这些不同传感器分别建立误差模型，并以此模型为基础进行数据融合[8]。

3）最后利用这个误差概率将观测值与全局航迹外推值进行融合，即zi=yiPi+xi（1-Pi），其中x代表观测值，y代表全局航迹外推值，z代表融合值，i代表维度。

例如以传统二维雷达为例，假设其理论距离误差为100米，方位误差为3度，最大量程为300公里。由于卡尔曼滤波是在直角坐标系下进行的，因此距离和方位误差会相互耦合，那么最大距离误差概率为Rmax×3×π/180，方位误差仍然约为3度。

需要注意的是在跟踪开始时刻，由于航迹需要时间收敛至接近真值，在未收敛之前的这段时间采用全局航迹进行误差概率估计会导致结果不准确。解决方法是在跟踪初始阶段直接采用观测值进行滤波，相当于将这一阶段的观测值误差概率设为0。

3 仿真实验

3.1 实验方法

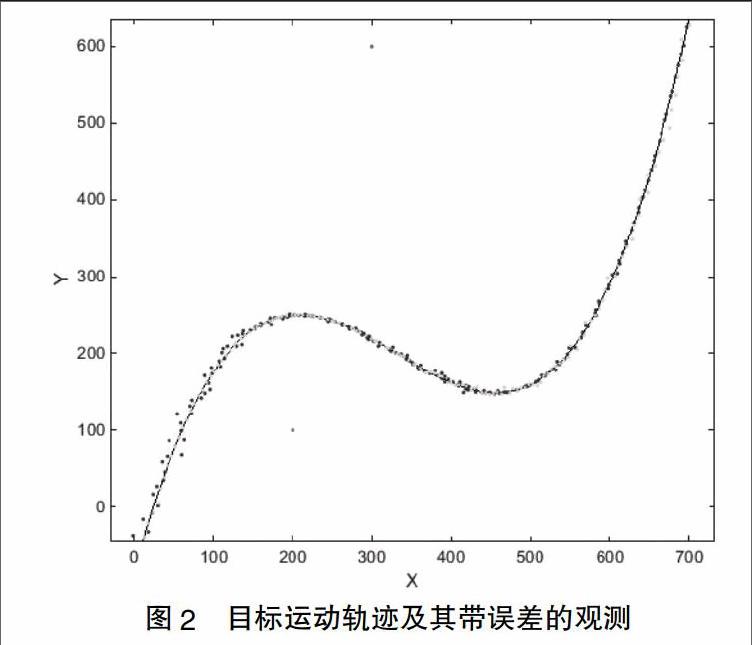
仿真实验模拟了两个传统两坐标雷达之间的数据融合。首先按照三次样条曲线等间隔生成了1000组观测值（以目标匀速曲线运动为条件），然后根据两个雷达的数据率分别在这1000组数据中抽取若干作为各雷达的观测，并加入方位误差（距离误差可忽略不计）。产生的数据如图2所示。

对产生的数据分别采用直接异步融合、同步估计融合、异步估计融合三种方法进行数据融合。其中直接异步融合是将两个雷达的观测点当作单传感器直接进行跟踪；同步估计融合将其中数据率低的雷达时间配准到数据率高的雷达观测时刻，然后进行同步融合；异步估计融合就是本文上一节讲到的方法。同步估计融合和异步估计融合全部采用误差概率估计方法对观测值进行参数估计。

3.2 实验结果

上述三种方法都采用相同的匀加速卡尔曼滤波器，最终的结果如图3、图4和表1所示。

4 总结

通过仿真对比试验，本文所提出的基于误差估计的集中式异步融合算法即保证的数据率，又使得精度得到了提高，其原因是同步融合中对观测值的外推时间跨度更大，因此引入的误差比采用全局航迹的外推更大，特别是在目标转弯时表现非常明显。

【参考文献】

[1]刘钊.多传感器时空一致及其信息融合技术研究[D].国防科学技术大学，2008.

[2]刘钊，戴斌.多传感器信息融合中时间同步方法的研究[J].计算机仿真，2009，26（6）：124-127.

[3]何俊，张华，刘继忠.基于耦合HMM的多传感异步信息融合分类策略[J].计算机应用研究，2009（8）：2836-2838.

[4]宋文尧.卡尔曼滤波[M].科学出版社，1991.

[5]韩崇昭.多源信息融合[M].清华大学出版社，2006.

[6]陶贵丽，邓自立.广义系统多传感器分布式融合降阶Kalman滤波器[J].科学技术与工程，2006，6（6）：661-668.

[7]刘磊，林雪原，周旻.多传感器组合导航系统的多尺度异步信息融合算法[J].海军航空工程学院学报，2012（3）：276-280.

[8]张士峰，蔡洪.Bayes分析中的多源信息融合问题[J].系统仿真学报，2000，12（1）：54-57.

[责任编辑：王伟平]