水平直肋管充分发展层流自然对流换热的数值分析

张倬

【摘 要】本文建立了水平直肋管层流自然对流换热的数学模型。通过对模型化简，导出无量纲控制方程，利用Simpler算法以及均分网格，对该问题进行求解，并进行了流场与温度场的数值模拟，分析了阻力系数和平均Nusselt数随Ra数变化曲线。与相关文献中的实验结果对比符合良好。

【关键词】水平直肋管；Simpler；自然对流；数值模拟

【Abstract】In this paper， established a mathematics model， based on laminar mixed convection in the fully developed region of horizontal internally finned tubes. According to the simple model assumption， got the non-dimension equation， then applied SIMPLER arithmetic and proportional grid to the computation， and analyzed the dynamic curve of resistance coefficient and average Nusselt number changed with Ra number. A matched numerical imitation was carried out.

【Key words】Horizontal internally finned tubes； SIMPLER； Spontaneous convection； Numerical imitation

0 引言

内肋管作为强化换热的一种有效的手段在工程中有着广泛的应用，对其进行数值分析有着十分重要的意义。在水平直肋管层流自然对流换热的研究中，横截面上的流动分析是一个难点，对其处理的方法关系到结果的正确性及准确性。本文根据Boussinesq假设建立了水平直肋管层流自然对流换热的数学模型，导出无量纲控制方程，利用Simpler算法对该问题进行求解。对于M=10，H=0.325，Pr=4.2，Gr+=3×105～2×106得到一系列结果，与相关文献中的实验与数值结果作了对比，相符良好。

文中各变量符号说明见表1。

1 数学模型及控制方程的建立

水平内肋管的截面图如图1所示。

管内流体作轴向流动，在截面上有自然对流。为使模型简单便于分析，现作以下简化假设：（1）肋片沿着径线方向且不计厚度；（2）流动处于稳态，层流；（3）流体轴向导热不计；（4）流动与换热已经进入充分发展状态；（5）流体受到轴向均匀热流加热，但周向壁温（包括翅片）均匀。

引入Boussinesq 假设成立，即（1）流体中的粘性耗散略而不计；（2）除密度外其他物性为常数；（3）对密度仅考虑动量方程中与体积力有关的项，其余各项中的密度亦作为常数。

4 算例计算及讨论

对M=10，H=0.325的内肋管在Pr=4.2，Gr+=3×105～2×106范围下进行求解，求解的结果包括截面速度分布、温度分布、阻力系数以及平均Nusselt数。

4.1 截面速度和温度分布

从图2（a）中可以看出截面上存在二次流，这是由浮力所导致，由此引发在截面顶部和底部之间流体的交换，此外，还可以看出在顶部流动不明显，而在底部强度较大。

图2（b）是截面上的温度分布图，从图中可以看出，接近截面顶部时温度变化缓慢，而在底部温度变化剧烈，温度最低点位于截面下半部分。这与截面二次流分布相吻合。

图2（c）为截面上相对轴向速度W/Wm分布，先对于二次流和温度的分布，轴向速度的分布相对均匀，受浮力影响较小。

4.2 阻力系数和Nusselt数

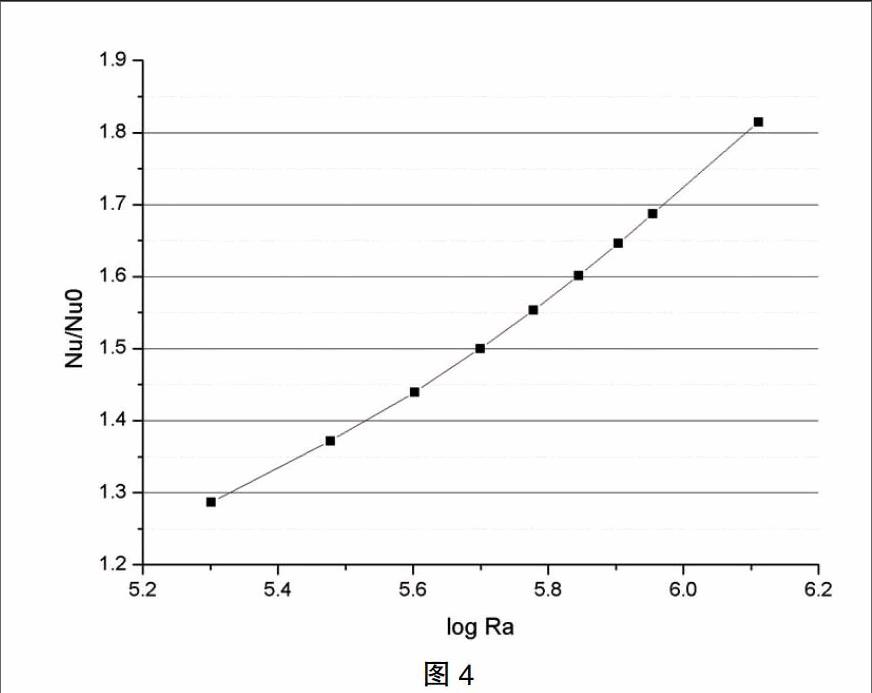
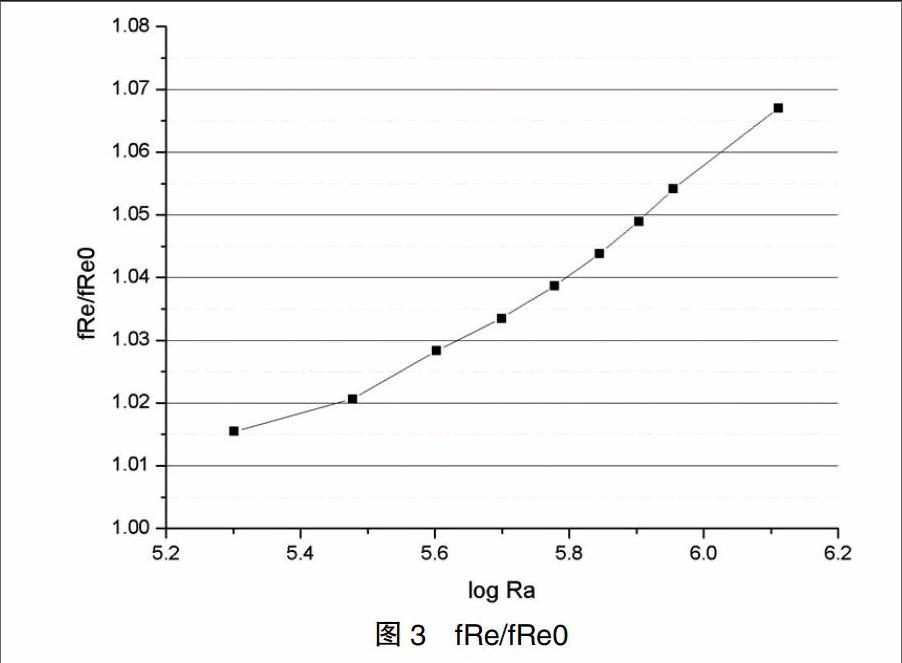
图3和图4为阻力系数和Nusselt数随Ra+变化情况，其中fRe0和分别为强制对流条件下的阻力系数和平均Nusselt数。由图可以看出各工况点下的fRe和与强制对流条件下fRe0和的比值fRe/fRe0和随Ra+增大而增大。这是由于随着Ra+的增大，截面上二次流加剧，阻力增大，换热系数也增大。上述的趋势与文献[1]中的基本吻合。

5 总结和建议

由于采用了某些简化假设，本文计算结果与工程实际必然存在差别，因此可以从以下几个方面着手对物理模型进行改善，以更好符合工程实际。（1）考虑肋片厚度，采用自适应网格确定肋片区域；（2）考虑轴向导热和黏性耗散，按三维求解；（3）周向壁温及热流密度按实际清况分布；（4）考虑肋片效率。

【参考文献】

[1]Rustum I.M.， Soliman H.M. Numerical analysis of laminar mixed convection in horizontal internally finned tubes[J]. Journal of Heat Mass Transfer， 1990， 33（7）：1485-1496.

[2]陶文铨.数值传热学[M].2版.西安：西安交通大学出版社，2001：115-123.

[3]王跃社，等.水平微肋管内基于气液环状流流型的沸腾传热理论模型[J].工程热物理学报，2007，28（S1）：177-180.

[责任编辑：杨玉洁]