新的基于身份无可信私钥生成中心的部分盲签名方案

刘二根　周华静,2　左黎明,2　王　霞,2

1(华东交通大学理学院　江西 南昌 330013)2(华东交通大学系统工程与密码学研究所　江西 南昌 330013)



新的基于身份无可信私钥生成中心的部分盲签名方案

刘二根1周华静1,2左黎明1,2王霞1,2

1(华东交通大学理学院江西 南昌 330013)2(华东交通大学系统工程与密码学研究所江西 南昌 330013)

摘要一般的基于身份的签名方案，存在密钥托管问题。对周萍等[10]提出的方案进行研究，发现该方案对于篡改公共信息攻击并不安全。因此，在原方案的基础上进行改进，给出一个新的基于身份无可信中心部分盲签名方案。随后证明了新方案在随机预言机模型下对于适应性选择消息和身份攻击是存在性不可伪造的，并证明了新方案可抗篡改公共信息攻击及满足部分盲性。通过与已有部分盲签名方案进行效率比较，发现新方案具有较高的效率。

关键词基于身份无可信私钥生成中心部分盲签名随机预言机模型

0引言

盲签名是数字签名中的一种，是由Chaum[1]在1982年首次提出的。所谓盲签名是指签名者在不知道消息的具体内容的情况下进行签名，并且当该签名公布后，签名者不能将自己的签名与消息对应，即满足不可追踪性。因此广泛应用与电子现金系统及匿名电子投票等，但是正是由于盲签名的这种完全匿名性，容易造成签名的滥用，这样会造成签名者的损失。1996年，Abe等[2]首次提出部分盲签名的概念，在部分盲签名中签名者和签名请求者事先商量好一个公共信息，成功解决了盲签名中签名的滥用问题。部分盲签名的这种优点得到学者的广泛关注，2001年，Chien等[3]基于RSA困难问题提出一个部分盲签名方案。

公钥密码系统包括基于证书、无证书及基于身份的密码体制，传统的基于证书密码体制中，由证书生成中心生成用户公钥证书来绑定用户身份，但是证书的颁发、存储、更新等占用很大花费。无证书密码体制由Al-Riyami和Paterson[4]在亚密会上首次提出的，该体制下不需要公钥证书，但是容易存在用户公钥被替换的风险。而Shamir[5]于1984年提出的基于身份密码体制将用户的身份等公共信息作为用户公钥，传统的基于身份密码体制需要一个可信中心生成用户私钥，这就存在密钥托管问题。2003年， Chen等[6]首次提出基于身份无可信私钥生成中心的密码学思想，并给出一个具体的签名方案。至此，基于各类密码体制学者们分别提出各种部分盲签名方案。2010年，李明祥等[7]提出一个高效的无证书部分盲签名方案，同年，冯涛等[8]给出一个安全的无可信PKG的部分盲签名方案。2012年，何俊杰等[9]提出一个高效的基于身份的部分盲签名方案。同年，周萍等[10]提出一个安全无可信私钥生成中心的部分盲签名方案。

本文，通过对文献[10]中部分盲签名方案的安全性分析，发现方案存在公共信息被篡改的危险，在此基础上提出改进方案。并证明了方案的安全性。

1预备知识

1.1双线性对映射

定义1设G1、G2分别为q阶加法循环群和乘法循环群。映射e:G1×G1→G2，满足下面三条性质则称为双线性对映射：

2) 非退化性：存在P,Q∈G1，使得e(P,Q)≠1；

3) 可计算性：对于任意的P,Q∈G1，存在有效的多项式时间算法能计算出e(P,Q)。

1.2离散对数问题(DLP)

假设1(离散对数困难性假设)假设算法Ω不能在多项式时间内以一个不可忽略的概率解得离散对数问题，则称离散对数困难性假设成立。

1.3安全模型[11]

一个安全的基于身份无可信中心的数字签名方案，必须满足正确性和不可伪造性。下面给出安全性和不可伪造性定义。

定义3(正确性)如果一个基于证书的数字签名方案是由签名人严格按照签名算法的步骤产生的，那么该签名能够通过验证等式，即该签名方案满足正确性。

下面定义基于证书数字签名的不可伪造性：

定义4(不可伪造性)如果不存在一个多项式时间(PPT)的攻击者F以不可忽略的概率借助挑战算法C伪造出的签名来赢得下面的游戏，则称此签名方案在适应性选择消息和身份下满足存在性不可伪造。

游戏(F和C参与游戏)

1) 初始化：挑战算法C运行系统初始化算法，生成系统公开参数并发送给攻击者F；

2) 询问：攻击者F可以在多项式时间内进行下列适应性询问：

① Hash询问：F可以向C进行任意的Hash询问；

② 密钥询问：F可以向C进行除目标用户外的任意用户的密钥询问；

③ 签名询问：F可以向C进行任意消息对应的签名询问。

3) 伪造：如果攻击者F通过上面的询问得到训练，且在询问过程中，F没有对目标用户的密钥和签名进行过询问，输出的一个伪造签名，并通过验证等式，则F赢得游戏。

2文献[10]方案回顾

2.1方案回顾

文献[10]给出一个无可信私钥生成中心的部分盲签名方案，该方案包括系统初始化、签名密钥生成、签名及验证四个算法组成，由签名者，请求者及验证者三个实体共同完成。具体方案描述如下：

1) 系统初始化(Setup)

2) 密钥生成(KeyGen)

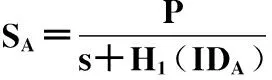
则用户公私钥对分别为(SA,x)，(PKA1,PKA2)；

3) 签名(Sign)签名者A身份为IDA，请求者B身份为IDB，待签名消息为m∈{0,1}*，设签名者与请求者事先协商好的公共信息为c，计算gc=e(H3(c),P1)并作为公钥参数公开，签名者和请求者进行如下交互：

(3) 签名：A收到盲化消息后，进行签名，计算S′=kxH3(c)+xh′H1(IDA)SA，将S′发送给B；

(4) 解盲：B收到盲签名后，进行解盲，计算S=αS′+βP+H1(IDA)H3(c)，则消息m的部分盲签名为σ=(S,h,c)。

2.2对方案的攻击

通过对上述方案的安全性分析，发现上述方案存在篡改公共信息攻击。如果攻击者将公共信息篡改，那么就会存在签名被滥用的可能，这会对签名者造成很大的损失或者伤害。具体攻击过程如下：

下面证明，如果被不诚实的用户T篡改过公共信息的签名能通过验证等式，则说明攻击者攻击成功，也即方案不能抵抗篡改公共信息攻击。

=e(H3(c),P1)αkxe(P,P1)βe(xP,P)αβH1(IDA)

=e(αkxH3(c),P1)e(βP,P1)e(xSA,P1)αβH1(IDA)

=e(αkxH3(c)+βP+xαβH1(IDA)SA,P1)

所以：

故：

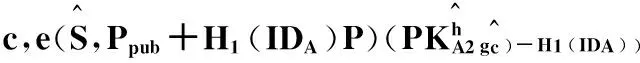
3方案改进

其中系统初始化阶段与文献[10]方案相同，不再赘述。只在密钥生成、签名和验证部分进行修改。

密钥生成：

则用户私钥对为(x,SKA)，公钥对为(PKA1,PKA2)。

签名：在该算法中，需要签名者与请求者进行交互才能完成，设签名者为A，身份为IDA，请求者B，身份为IDB，消息m∈{0,1}*，签名者与请求者事先协商好的公共信息为c，交互过程如下：

3) 签名：A收到h′后，进行签名，计算S′=kxH3(c)+h′H1(IDA)SKA+xP，将S′发送给B；

4) 解盲：B收到盲签名S′后，解盲，计算S=αS′，则关于m的消息签名对为σ=(S,m,h,r,c)。

验证：验证者收到签名对σ=(S,m,h,r,c)后，验证等式r=e(S,Ppub+H1(IDA)P)g-hH1(IDA)是否成立。如果成立，说明签名有效；否则，签名无效。

4新方案的安全性分析

4.1正确性

定理1改进后的部分盲签名方案是正确的。

证明：只需证明签名可以通过验证等式即可。

e(S,Ppub+H1(IDA)P)g-hH1(IDA)

=e(αS′,Ppub+H1(IDA)P)g-hH1(IDA)

=e(αkxH3(c)+hH1(IDA)SKA+

αβH1(IDA)SKA+αxP,P1)g-hH1(IDA)

=e(H3(c),P1)αkxe(SKA,P1)hH1(IDA)

e(SKA,P1)αβH1(IDA)e(xP,P1)αg-hH1(IDA)

因此，验证等式成立，即方案满足正确性。

4.2部分盲性

定理2改进后的部分盲签名方案满足部分盲性。

S=αS′

(1)

h′=α-1h+β

(2)

(3)

由式(1)可以唯一确定α=logS′S，又由式(2)唯一确定β=h′-α-1h，只要此唯一确定的α、β满足式(3)即可。

因为签名是有效的，因此满足验证等式，有：

r=e(S,Ppub+H1(IDA)P)g-hH1(IDA)

=e(αS′,Ppub+H1(IDA)P)g-hH1(IDA)

=e(αkxH3(c)+hH1(IDA)SKA+

αβH1(IDA)SKA+αxP,P1)g-hH1(IDA)

=e(H3(c),P1)αkxe(SKA,P1)hH1(IDA)

e(SKA,P1)αβH1(IDA)e(xP,P1)αg-hH1(IDA)

即由式(1)、式(2)唯一确定的α、β可以使得式(3)成立，也就是说存在唯一的α、β使得某个有效签名与中间视图相对应。这样，签名者即使签了名，日后也无法将自己的签名与自己的签名过程联系起来，即满足了部分盲性。

4.3公共信息不可篡改性

定理3改进后的部分盲签名方案可以抵抗篡改公共信息攻击。

证明：改进后的方案在签名等式中无法完整地提取出含有公共信息的H3(c)来，因此如果攻击者想在解盲阶段将公共信息替换，通过将原本的H3(c)消掉是不可行的，也就是说攻击者无法替换公共信息。因此，改进方案可以抵抗篡改公共信息攻击。

4.4不可伪造性

定理4改进后的新的基于身份无可信中心的部分盲签名方案在随机预言机模型下，基于离散对数困难性假设，对于适应性选择消息及身份攻击满足存在不可伪造性。

证明：假设存在一个攻击者F，可以在多项式时间内成功伪造一个有效签名，那么只需证明存在一个概率多项式时间算法的挑战者C能够解决DL问题。这与离散对数困难性矛盾，因此方案满足存在不可伪造性。

DL问题实例为，已知(P,aP)，求解a。在证明中，假设F模拟用户进行攻击，C模拟公钥生成中心回答对F一系列询问，包括任意的哈希询问，部分密钥询问，个人密钥询问及签名询问，C通过模拟回答F的询问维护相应的列表：L1(IDi,h1i)，L2(mi,ci,ri,h2i)，L3(ci,h3i)，Lk(IDi,SKi,PKi1)，Lk′(xi,PKi2)，Ls(mi,hi,ri,ci,Si)。设目标用户的身份用ID*表示，C首先生成并公布系统公开参数params，置系统主私钥为a。下面由F进行如下询问：

H1询问F向C进行身份为IDi的H1询问，C首先查询列表L1，如果L1中存在(IDi,h1i)的项，直接返回h1i给F；否则，C随机选取h2i∈RZq*，将h1i返回给F并将(IDi,h1i)添加到列表L1中。

H2询问F向C进行消息为mi的H2询问，相应的公共信息为ci，签名公开参数为ri，C查询列表L2，若如果列表中存在(mi,ci,ri,hi)的项，直接hi给F；否则，C随机选取hi∈RZq*，将其返回给F并添加到列表L2中。

部分密钥询问F向C进行用户身份为IDi的部分密钥询问，C查询相应的列表Lk，如果列表中出现(IDi,SKi,PKi1)的项，直接返回(SKi,PKi1)给F；否则，假设已经之前已经进行过H1询问，不然可以先进行H1询问：

2)IDi=ID*时，C拒绝回答部分私钥，计算PKi1=e(P,P1)，其中P1=Ppub+h1iP，返回(-,PKi1)给F。

且无论上述1)，2)中的哪种情况都将其返回值添加到列表Lk中。

个人密钥询问F向C询问身份为IDi的用户个人密钥，C首先查询列表Lk′，如果列表中已经存在(xi,PKi2)的项，直接将其返回给F；否则：

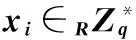
2)IDi=ID*时，C拒绝回答个人私钥，返回(-,PKi2)给F。

无论上述1)，2)中的哪种情况都将返回值添加到列表Lk′中。

签名询问F向C进行消息为mi的签名询问，C查询列表Ls，如果列表中已经存在Ls(mi,hi,ri,ci,Si)的项，直接返回Si给F；否则，假设在此之前已经进行过哈希询问，不然先进行上述询问：

1)IDi≠ID*时，C查询列表L1，L2，L3，分别得到h1i，hi，h3i的值，并随机选取Si，根据验证等式，计算ri=e(Si,Ppub+h1iP)g-hih1i。最后将消息签名对σi=(Si,mi,hi,ri,ci)返回给F。

2)IDi=ID*时，C拒绝回答，询问终止。

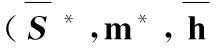
r*=e(S*,Ppub+H1(ID*)P)g-h*H1(ID*)

所以，有：

e(S*,Ppub+H1(ID*)P)g-h*H1(ID*)

即：

因此：

解得:

也就是说挑战者C成功解决了离散对数问题。这与离散对数困难性假设矛盾，因此说明攻击者无法攻破该方案。即方案在适应性选择消息和身份攻击下对于超级攻击者F是存在性不可伪造的。

5结语

将本文改进后的方案与文献[8-10]中发方案进行效率比

较，已知双线性对运算的时间复杂度最大，其次是哈希运算，指数运算次之，标量乘运算的时间复杂度基本忽略。用P表示双线性对运算，H表示哈希运算，E表示指数运算，M表示标量乘运算。比较结果如表1所示。

表1　各方案效率比较

由表1，本文提出的改进方案及文献[10]中的方案在整个过程中仅仅使用了一次双线性对运算，且改进后的方案比原方案使用了更少的哈希运算、指数运算及标量乘运算。因此，改进后的方案具有较高的效率。

参考文献

[1] Chaum D.Blind Signature for Untraceable Payments[C]//Proceeding of the Crypto’82.New York: Plenum Publishing,1982:145-152.

[2] Abe M,Fujisaki E.How to Date Blind Signatures[C]//Proceeding of the Cryptology-AsiaCrypt’96.Heidelberg:Springer-Verlag,1996:244-251.

[3] Chien H Y,Jan J K,Tseng Y M.RSA-Based Partially Blind Signature with Low Computation[C]//IEEE 8thInternational Conference on Parallel and Distributed Systems,2001:385-389.

[4] Al-Riyami S,Paterson K G.Certificateless public key cryptography[C]//Proc. of Cryptology-ASIANCRYPT’03.Berlin,Germany:Springer-Verlag,2003:452-473.

[5] Shamir A.Identity-based cryptosystems and signature schemes[C]//Proceedings of Crypto’84.Berlin:Springer-Verlag,1984,LNCS 196:47-53.

[6] Chen Xiaofeng,Zhang Fangguo,Kim K.A New ID-based Group Signature Scheme from Bilinear Pairings[C]//Proceedings of WISA’03,2003:585-592.

[7] 李明祥,杜光辉,罗新方.高效的无证书部分盲签名方案[J].计算机工程与设计,2010,31(22):4817-4819,4892.

[8] 冯涛,彭伟,马建峰.安全的无可信PKG的部分盲签名方案[J].通信学报,2010,31(1):128-134.

[9] 何俊杰,王娟,祁传达.安全高效的基于身份的部分盲签名方案[J].计算机应用,2012,32(5):1388-1391.

[10] 周萍,何大可.安全无可信私钥生成中心的部分盲签名方案[J].计算机系统应用,2012,21(6):70-74.

[11] Boneh D,Boyen X.Short Signatures without Random Oracles[C]//LNCS 3027,Advances in Cryptology: Proc. Eurocrypt’04,Springer,2003:56-73.

[12] Pointcheval D,Stern J.Security Proofs for Signatures[C]//LNCS 1070,Advances in Cryptology:Proc.Eurocrypt’96,Springer,1996:387-398.

[13] 文佳骏,左黎明,李彪.一个高效的无证书代理盲签名方案[J].计算机工程与科学,2014,36(3):452-457.

NEW ID-BASED PARTIALLY BLIND SIGNATURE SCHEME WITHOUT TRUSTED PRIVATE KEY GENERATOR

Liu Ergen1Zhou Huajing1,2Zuo Liming1,2Wang Xia1,2

1(SchoolofScience,EastChinaJiaotongUniversity,Nanchang330013,Jiangxi,China)2(SECInstitute,EastChinaJiaotongUniversity,Nanchang330013,Jiangxi,China)

AbstractGeneral ID-based signature schemes have the problem of key escrow. We studied the signature scheme presented by Zhou Ping et al[10], and found that the scheme is not secure for tampering public information attack. Hence, we made improvement based on the original scheme and put forward a new ID-based partial blind signature scheme without trusted centre. Subsequently, we proved that the new scheme was existentially unforgeable under random oracle model against adaptive chosen message and identity attack, and that the new scheme was also able to resist tampering public information attack, as well as satisfied the partial blindness. By comparing with other partially blind signature schemes in efficiency, we found that the new scheme had higher efficiency.

KeywordsID-basedWithout trusted private key generatorPartially blind signature schemeRandom oracle model

收稿日期：2014-12-23。国家自然科学基金项目(11061014，6124 0025)；江西省高校科技落地计划项目(KJLD12067)；江西省教育厅科研项目(GJJ13339)；华东交通大学校立科研基金项目(11JC04)。刘二根，教授，主研领域：图论及其应用。周华静，硕士生。左黎明，副教授。王霞，硕士生。

中图分类号TP309

文献标识码A

DOI:10.3969/j.issn.1000-386x.2016.05.071