基于混合演化策略算法的多场桥调度优化

刘志雄　李　俊　张　煜　东经伟

1(武汉科技大学汽车与交通工程学院　湖北 武汉 430081)2(武汉理工大学物流工程学院　湖北 武汉 430063)3(天津港集装箱码头有限公司　天津 300456)



基于混合演化策略算法的多场桥调度优化

刘志雄1李俊1张煜2东经伟3

1(武汉科技大学汽车与交通工程学院湖北 武汉 430081)2(武汉理工大学物流工程学院湖北 武汉 430063)3(天津港集装箱码头有限公司天津 300456)

摘要针对集装箱堆场多场桥调度问题，构建调度模型，提出一种混合演化策略算法。采用基于实数的四维个体编码方法，设计了基于三点交叉互换的重组算子以及基于两点互换的变异算子，并采用三种不同的局部搜索策略来优化算法的性能。通过算例分析证明混合演化策略算法在优化多场桥调度问题时的有效性。在三种不同的局部搜索策略中，基于互换操作的局部搜索策略要优于其他两种，能明显改善演化策略算法的优化性能。最后，通过一组对比试验对局部搜索的次数进行了分析。

关键词多场桥调度演化策略算法局部搜索

0引言

集装箱运输的迅猛发展给港口的作业能力带来了巨大的挑战。由于集装箱码头的改建和设备投入都需要大量的资金注入，因此如何充分利用现有资源来提升码头装卸作业效率成为了当下的研究热点。堆场作为堆存集装箱的重要场地，在整个码头作业中起到缓冲作用，对整个码头的装卸作业效率、吞吐能力以及船舶在港时间等都有很大的影响。在现有的岸边作业系统和水平运输系统一定的情况下，堆场作业效率成为了制约码头吞吐能力的瓶颈，而场桥作为堆场作业中的核心设备，是提高堆场作业效率的关键。如何对场桥进行有效地调度，从而保障整个堆场的作业效率是亟需解决的问题。

目前，针对集装箱堆场场桥调度问题，国内外学者分别设置不同的规则，采用算法求解或是仿真建模的方法进行了优化研究。陈欢[1]建立了多台场桥作业动态调度的模型，采用贪婪算法进行优化求解，并基于AnyLogic软件构建了仿真模型。王岩[2]以完成装箱任务时场桥最大移动时间最短为目标建立了多台场桥的路径优化模型，设计了进化规划算法进行优化求解。贾志刚[3]以延迟任务量、转场总时间与空闲总时间三者最小化为目标构建了场桥的调度模型，将启发式算法和遗传算法结合来优化求解。牟莲芝[4]构建了场桥的优化调度模型，设计了蚁群算法进行优化求解。张琪[5]构建了考虑干涉的多场桥调度优化模型，设计了一些调度规则进行编程求解。乐美龙等[6]考虑场桥在实际作业中不可相互跨越与安全距离等约束，建立了场桥作业调度模型，设计了两阶段启发式算法进行求解。赵磊等[7]以堆场箱区作业箱量均衡和作业时间均衡为目标建立了场桥均衡调度模型，并设计遗传算法求解。何军良等[8]将场桥调度和堆存空间分配作为整体考虑，构建了场桥的动态调度模型，设计了基于整数规划模型和启发式算法来进行求解。严伟等[9]以到各时段中剩余总工作量最小为目标构建了基于整数规划的场桥动态调度模型，采用最佳优先搜索算法进行优化求解。K．L．Mak等[10]通过遗传算法和禁忌搜索的混合算法，求解带有机器干涉约束的场桥调度问题。H.Javanshir等[11]考虑场桥的干涉约束，构建了混合整数规划模型，采用遗传算法进行模型的优化求解。这些文献大多都没考虑场桥转向次数过多的问题，而在实际作业中场桥的转向次数过多将直接影响整个堆场的作业效率。

本文将在考虑最短路的前提下，以减少场桥的转向次数和最小化场桥的最大作业完工时间为目标，构建多目标的多场桥优化调度模型。针对构建的模型，设计一种混合演化策略算法进行优化求解。最后，根据天津港集装箱码头堆场的实际情况，设置几种规模不同的作业场景来验证模型以及算法的有效性。

1多场桥调度问题

对进口箱作业而言，当岸桥把集装箱从船舶上卸载下来以后，放到集卡上，然后由集卡水平运输到堆场进行堆存。由于具有空箱位的贝位往往在不同的箱区内，为了保证场桥作业的均衡，场桥往往需要进行转场作业，同时在转场时，若前后作业的两个箱区不在同一条直线上，场桥还需要进行转向。由于场桥胎压较高，转向时对轮胎会有一定程度的磨损，同时场桥在转向时会在通道上花费大量时间，导致道路的拥堵，影响集卡和其他场桥的通行，因而场桥的转向不仅会增加设备的使用成本，也会降低堆场的整体作业效率。

多场桥调度问题是指针对堆场内某一时间段内的堆箱作业任务，安排多台场桥来共同完成，这时就需要在保证堆箱顺序的前提下，考虑场桥移动的最短距离，对多个场桥进行移动，确定每台场桥的行走路径，明确场桥每次作业的贝位位置以及在该贝位位置上的作业箱量，最后在该时间段的堆箱作业任务全部完成时，在保证参与作业的所有场桥的转向次数尽量小的同时，使所有场桥的最大作业完工时间最小化。

1.1贝位的坐标表示

图1　贝位位置坐标的说明示意图

由于集装箱码头堆场的布局一般都很规整，为了确定每个时刻场桥所在的贝位(bay)位置，现采用一种三维坐标的形式(x，y，z)来对堆场内的贝位进行编码。其中第一维x表示箱区(block)所在的列，第二维y表示箱区所在的行，第三维z表示箱区内的贝位号。如图1所示，图中标“1”的贝位位置可以表示为(1，1，4)，标“2”的贝位位置可以表示为(2，1，6)，标“3”的贝位位置可以表示为(3，1，10)，标“4”的贝位位置可以表示为(1，2，3)，标“5”的贝位位置可以表示为(1，3，7)，标“6”的贝位位置可以表示为(3，3，4)。这样每个贝位位置就可以用唯一的坐标来表示，方便调度模型的求解。

1.2模型假设

针对天津港集装箱码头堆场的实际情况，对构建的模型做出以下几点假设：

(1) 堆场内所有场桥的作业能力等基本参数相同；

(2) 不存在多台场桥处于同一贝位产生冲突的情况；

(3) 忽略堆场中集卡阻塞对场桥调度的影响；

(4) 每个箱区在任意时刻至多只有2台场桥；

(5) 只考虑普通箱的堆存情况；

(6) 不考虑场桥作业的等待时间。

1.3参数定义

M：堆场内的场桥总数(单位：台)

N：堆场内的箱区数(单位：个)

Dx：两水平相邻箱区间的水平距离(单位：米)

Dy：两垂直相邻箱区间的垂直距离(单位：米)

LXi：箱区i的长度(i=1，2，…，N)(单位：米)

WX：箱区的宽度(单位：米)

Bi：箱区i内的贝位数(i=1，2，…，N)(单位：个)

LB：单个贝位的长度(沿箱区长度方向)(单位：米)

q：场桥的作业效率(单位：TEU/分)

v：场桥的水平移动速度(单位：米/秒)

tr：场桥完成一次90°转弯所需的时间(单位：秒)

Cxyz：贝位(x，y，z)的空箱位(单位：个)

Q：需要进行堆存的总作业箱量(单位：TEU)

ni：场桥i的总作业次数(i=1，2，…，M)(单位：次)

Qij：场桥i的第j次作业的作业箱量(i=1，2，…，M；j=1，2，…，ni)(单位：TEU)

DTij：场桥i到达第j次作业贝位位置所需要的移动时间(i=1，2，…，M；j=1，2，…，ni)(单位：秒)

Aij：场桥i到达第j次作业贝位位置是否需要90°转向的决策变量，若需要90°转向，则Aij的值为1，否则为0(i=1，2，…，M；j=1，2，…，ni)

1.4调度模型

调度模型的优化目标是在考虑最短路的前提下，减少场桥转向次数的同时，最小化场桥的最大作业完工时间。其中，场桥i的第j次作业完工时间由上次作业完工时间与本次堆箱作业时间以及到达本次作业贝位的移动时间，可以表示为：

(1)

其中场桥移动时间DTij需要分以下三种情况来进行确定：

(1) 场桥i的第j次作业的贝位位置与上次作业位置位于同一列

假设某集装箱堆场的平面示意图如图2所示，场桥i的第j次作业的贝位位置在图中标“2”位置，上一次作业贝位位置在图中标“1”位置。那么场桥在从位置“1”到达位置“2”时，既可以向左移动后经过两次90°转向后再到达，也可以向右移动后经过两次90°转向后再到达。这时就需要对这两条场桥的行走路径进行最短路的判断，让场桥选择最短路径进行转场作业。

图2　场桥前后作业贝位位于同一列路径选择示意图

通过上述分析可以得出此时的DTij可以表示为：

DTij=Aij×2tr+

(2)

其中，min{}表示需要进行场桥最短路的判断。

(2) 场桥i的第j次作业的贝位位置与上次作业位置位于相邻两列

此时，需要考虑场桥向左移动和向右移动两种情况：

① 场桥i的第j次作业的贝位位置位于上次作业位置左侧，则场桥需要向左移动。假设场桥前后两次作业的贝位位置如图3所示，场桥i的第j次作业的贝位位置在图中标“2”位置，上一次作业贝位位置在图中标“1”位置。那么场桥在从位置“1”到达位置“2”时，按照最短路的原则，场桥会按图中箭头所示的方向进行移动。

图3　场桥前后作业贝位位于相邻两列向左移动路径示意图

因此在此种情况下，若场桥向左移动，则DTij可以表示为：

(3)

② 场桥i的第j次作业的贝位位置位于上次作业位置右侧，则场桥需要向右移动。假设场桥前后两次作业的贝位位置如图4所示，场桥i的第j次作业的贝位位置在图中标“2”位置，上一次作业贝位位置在图中标“1”位置。那么场桥在从位置“1”到达位置“2”时，按照最短路的原则，场桥会按图中箭头所示的方向进行移动。

图4　场桥前后作业贝位位于相邻两列向右移动路径示意图

因此在此种情况下，若场桥向右移动，则DTij可以表示为：

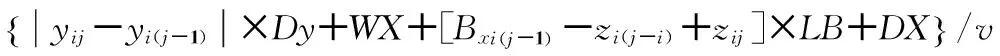
(4)

(3) 场桥i的第j次作业的贝位位置与上次作业位置位于不相邻两列

此时，需要考虑场桥向左移动和向右移动两种情况：

① 场桥i的第j次作业的贝位位置位于上次作业位置左侧，则场桥需要向左移动。

假设场桥前后两次作业的贝位位置如图5所示，场桥i的第j次作业的贝位位置在图中标“2”位置，上一次作业贝位位置在图中标“1”位置。那么场桥从位置“1”到达位置“2”时，按照最短路的原则，场桥可以按图中箭头所示的方向任意选择一条路径进行移动。这是因为若前后两位作业贝位之间不在同一行，则场桥会有多条行走路径，但是每条路径的所需的行走时间都是一样的，这时场桥可以根据堆场的实时情况，选择一条不与其他场桥产生作业干涉的路径进行移动。

图5　场桥前后作业贝位位于不相邻两列向左移动路径示意图

因此在此种情况下，若场桥向左移动，则DTij可以表示为：

(5)

其中，k={xi(j-1)，xi(j-1)+1，…，xij-1}，∑LXk表示需要加上中间所有箱区的长度。

② 场桥i的第j次作业的贝位位置位于上次作业位置右侧，则场桥需要向右移动。

假设场桥前后两次作业的贝位位置如图6所示，场桥i的第j次作业的贝位位置在图中标“2”位置，上一次作业贝位位置在图中标“1”位置。那么场桥在从位置“1”到达位置“2”时，按照最短路的原则，与上面场桥向左移动的情况一样，场桥同样有多条行走路径可以来选择，这时场桥可以按图中箭头所示的方向任意选择一条不与其他场桥产生作业干涉的路径进行移动。

图6　场桥前后作业贝位位于不相邻两列向移动路径示意图

因此在此种情况下，若场桥向右移动，则DTij可以表示为：

(6)

其中，k={xi(j-1)，xi(j-1)+1，…，xij-1}，∑LXk表示需要加上中间所有箱区长度。

根据式(1)—式(6)可以求出每台场桥i的作业完工时间Tini：

(7)

则目标函数可以表示为：

(8)

(9)

式(8)表示最小化所有场桥的总转场次数，式(9)表示最小化所有场桥的最大作业完工时间。

约束条件：

(10)

(11)

Cxij yij zij≥Qij

(12)

0≤i≤M

(13)

0≤j≤ni

(14)

式(10)表示所有场桥的作业量之和等于需要进行堆存的总作业箱量；式(11)表示所有场桥作业贝位的空箱位应该不小于需要进行堆存的总作业箱量；式(12)表示场桥在某一贝位的作业时，该贝位的空箱位应该不小于其作业箱量；式(13)与式(14)表示对循环变量的约束。

2多场桥调度优化的演化策略算法设计

演化策略算法主要包含了选择策略、重组算子和变异算子三大部分，其中选择策略存在(1+1)、(μ+1)、(μ+λ)和(μ，λ)等几种不同的形式。本文采用基于(μ+λ)选择策略的演化策略算法，考虑加入几种不同的局部搜索策略来优化算法的求解性能，设计一种混合演化策略算法来对多场桥调度问题进行优化。

2.1个体编码

(1) 个体编码方法

采用基于实数的四维个体编码方法，第一维表示贝位序号，第二维表示个体位置，在[0，2]区间内随机生成来对贝位加工顺序进行排序，第三维表示每个贝位的作业箱量，第四维用来确定到每个贝位作业的场桥编号。

假设有m台场桥到n个贝位去进行堆箱作业，每个贝位的个体位置分别为Xi(i=1，2，…，n)，每个贝位的作业箱量分别为Ci(i=1，2，…，n)，每个贝位作业的场桥编号为Qi∈[1，m](i=1，2，…，n)，则一个完整的四维粒子可以如表1所示来表示。

表1　基于实数的四维个体编码方法

(2) 个体解码

首先，按照第二维个体位置Xi的大小对第一维贝位序号进行从新排序，得到所有贝位的作业先后顺序，同时需要相应地调整第三维和第四维的位置。然后，根据第四维场桥编号Qi来得到每个贝位的作业场桥，从而得到每个场桥的作业贝位集合，根据每个场桥的作业贝位集合以及贝位的先后作业顺序，就可以得到每个场桥的行走路径，从而就可以计算出场桥的转向次数及其对应的作业完工时间。

2.2重组算子

采用基于三点交叉互换的重组算子，依次针对个体的第二维和第四维个体编码进行重组，其实现过程如下：首先随机选取两个父代个体，然后在它们的第二维(或第四维)个体编码中随机选择三个交叉点，从而将其分成了四段，然后采取隔段互换的方式进行基因值的互换，从而产生了两个子代个体，如图7所示。

图7　基于三点交叉互换的重组算子

2.3变异算子

在生成的子代个体中，采用基于个体内部基因两点互换的变异算子，依次针对其第二维和第四维个体编码进行变异，其实现过程如下：在子代个体中，随机选择两个不同的位置，交换这两个位置上第二维(或第四维)个体编码的基因值，从而生成新的子代个体，如图8所示。

图8　基于两点互换的变异算子

2.4局部搜索策略

在进行了(μ+λ)选择策略以后，针对新产生的μ个父代个体进行局部搜索。局部搜索用来实现对每个父代个体在其邻域内进行局部最优解的搜索过程。采用三种基于邻域操作的局部搜索策略：基于互换操作、基于逆序操作以及基于插入操作的局部搜索策略[12]。

(1) 基于互换的局部搜索方法

依次针对父代个体的第二维和第四维个体编码进行互换操作。基于互换的局部搜索方法按以下步骤来实现：① 对于每一个父代个体，随机选择其第二维(或第四维)个体编码中的两个不同位置p、q(p

(2) 基于逆序的局部搜索方法

依次针对父代个体的第二维和第四维个体编码进行逆序操作。基于逆序的局部搜索方法按以下步骤来实现：① 对于每一个父代个体，随机选择其第二维(或第四维)个体编码中的两个不同位置p、q(p

(3) 基于插入的局部搜索方法

依次针对父代个体的第二维和第四维个体编码进行插入操作。基于插入的局部搜索方法按以下步骤来实现：① 对于每一个父代个体，随机选择其第二维(或第四维)个体编码中的两个不同位置p、q(p

3试验结果与分析

3.1算例求解

目前，北方某集装箱码头堆场用来进行普通箱堆存的区域主要有31～38场、41～48场、51～56场以及71～74场，一共26个场。这26个场在堆场中的分布情况如图9所示。

图9　堆场分布实际情况图

(1) 2台场桥到10个贝位作业的算例

假设现在有2台场桥来完成180个箱的堆存任务，这180个箱需要堆存到10个贝位上。随机生成2台场桥的初始位置和10个贝位的位置以及各贝位上的作业箱量如表2所示。

表2　算例1原始数据表

在考虑最短路的前提下，以场桥转向次数最少和最小化最大作业完工时间为目标，其中以优化场桥转向次数为主，分别采用演化策略算法(ES)和混合演化策略算法(HES)对上述算例进行优化求解，其中，ES和HES的基本参数设置均为μ=40、λ=30，最大迭代次数100次，HES采用每种局部搜索策略的次数均为3次。同时，采用常见的粒子群算法(PSO)和模拟退火算法(SA)来进行结果对比分析。为了使这两种算法的求解性能更优，将PSO的参数设置为种群数量为50，学习因子均为2，采用线性递减的惯性权重(从0.9线性递减至0.4)，最大迭代次数为1000次；将SA的参数设置为初始温度T0=1000，结束温度Te=0.001，Metropolis链长L=200，降温速率q=0.98。所有的算法均连续优化20次，优化结果如表3所示。

表3　算例1不同算法优化结果表

注：表中每种算法下第一列表示转向次数(单位：次)，第二列表示最大作业完工时间(单位：min)

从表3的结果中可以看出，ES和HES在迭代次数更少的前提下，具有更高的求解效率和更好的求解结果，它们优化性能要明显好于PSO和SA。由于算例较为简单，采用局部搜索策略对HES求解性能的优化效果并不十分明显。

(2) 4台场桥到10个贝位作业的算例

假设现在有4台场桥来完成180个箱的堆存任务，这180个箱需要堆存到10个贝位上。这4台场桥的初始位置和10个贝位的位置以及各贝位上的作业箱量如表4所示。

表4　算例2原始数据表

同样在考虑最短路的前提下，以场桥转向次数最少和最小化最大作业完工时间为目标，其中以优化场桥转向次数为主，采用ES、HES、PSO、SA来进行优化求解。为了保证算法的求解性能，对某些算法的相关参数做以下调整：SA的Metropolis链长调整为L=300，其他参数与上一算例保持一致；ES和HES的最大迭代次数调整为300次，其他参数与上一算例保持一致；PSO的参数与上一算例保持一致。所有的算法均连续优化20次，优化结果表5所示。

表5　算例2不同算法优化结果表

注：表中每种算法下第一列表示转向次数(单位：次)，第二列表示最大作业完工时间(单位：min)

从表5的结果中可以看出，虽然PSO的求解时间是最短的，但是在迭代次数更少的前提下，ES和HES的求解结果要明显优于PSO和SA，且求解时间的差异不大。同时，随着场桥数量的增加，ES和HES均找到了最优解，但是采用局部搜索策略的HES的求解结果在稳定性方面要优于ES。且在三种不同的局部搜索策略中，采用基于互换操作的局部搜索策略的HES具有更好的求解效果。

(3) 4台场桥到20个贝位作业的算例

假设现在有4台场桥来完成360个箱的堆存任务，这360个箱需要堆存到20个贝位上。这4台场桥的初始位置和20个贝位的位置以及各贝位上的作业箱量如表6所示。

表6　算例3原始数据表

同样在考虑最短路的前提下，以场桥转向次数最少和最小化最大作业完工时间为目标，其中以优化场桥转向次数为主，采用ES、HES、PSO、SA来进行优化求解。为了保证算法的求解性能，对某些算法的相关参数做以下调整：PSO的最大迭代次数调整为2000次，其他参数与上一算例保持一致；ES和HES的最大迭代次数调整为500次，其他参数与上一算例保持一致；SA的参数与上一算例保持一致。所有的算法均连续优化20次，优化结果表7所示。

表7　算例3不同算法优化结果表

注：表中每种算法下第一列表示转向次数(单位：次)，第二列表示最大作业完工时间(单位：min)

从表7的结果中可以进一步看出，在迭代次数更少的前提下，ES和HES的求解结果要明显优于PSO和SA。同时，随着算例规模的增大，与ES相比，采用了局部搜索策略的HES具有更好的求解性能，且在三种不同的局部搜索策略中，基于互换操作的局部搜索策略对HES求解性能的优化效果更为理想。

3.2局部搜索次数分析

在局部搜索策略中，局部操作次数的设置是一个很重要的参数。局部搜索次数过少，则局部搜索对算法性能的优化效果不明显，无法体现局部搜索的作用；局部搜索次数过多，则会加大算法的搜索空间，对算法的求解效率产生影响。以算例3为例，设置几组不同的局部搜索次数，采用基于互换操作的混合演化策略算法(HES)来进行优化，通过对比试验来确定合适的局部搜索次数。其中，HES的基本参数设置为μ=40、λ=30，最大迭代次数500次。连续优化20次，优化结果如表8所示。

表8　不同局部搜索次数算法优化结果表

注：表中每组互换次数下第一列表示转向次数(单位：次)，第二列表示最大作业完工时间(单位：min)

设置不同局部搜索次数时，算法取得的平均转向次数以及平均最大作业完工时间如图10、图11所示，算法的平均求解时间如图12所示。

图10　算法平均转向次数折线图

图11　算法平均最大作业完工时间折线图

图12　算法平均求解时间折线图

从表8和图10、图11中可以看出，算法的求解结果与局部搜索次数之间并没有明显的规律可循，它并不是随着局部搜索次数的增加而越来越优，而是呈现出波动的情况。而从图12可以看出算法的平均求解时间却是随着局部搜索次数的增加而直线增加。所以必须设置一个合适的局部搜索次数在保障算法求解结果的同时提高算法的求解效率，缩短求解时间。

从表8中可以看出，当局部搜索次数设置为3次、4次、6次、8次时，算法求得的最优解更好。但是为了保障算法的稳定性和求解效率，从平均解和平均求解时间的角度出发，将局部搜索次数设置为3次更为合理。

4结语

首先针对集装箱堆场布局规整的特点设计了一种三维坐标表示方法来确定堆场中的贝位位置。然后，从考虑场桥最短路的角度出发，构建了多场桥调度的优化模型，该模型在优化场桥转向次数的前提下，对场桥的最大作业完工时间进行优化。针对构建的多场桥调度模型，采用基于局部搜索策略的混合演化策略算法(HES)来优化求解。通过几个算例的试验说明，HES比传统的演化策略算法(ES)和常见的粒子群算法(PSO)、模拟退火算法(SA)具有更好的优化性能，且在采用基于互换操作的局部搜索策略时，对算法的性能优化效果更加理想。最后，通过一组对比实验对局部搜索的次数进行了分析，得出了将局部搜索次数设置为3次较为合理。

参考文献

[1] 陈欢．集装箱场桥调度及其仿真研究[D]．武汉：武汉理工大学，2011．

[2] 王岩．集装箱堆场多桥路径优化研究[D]．大连：大连海事大学，2012．

[3] 贾志刚．集装箱码头箱区间场桥调度研究[D]．大连：大连海事大学，2013．

[4] 牟莲芝．集装箱码头闸口-场桥合理配置的仿真优化研究[D]．大连：大连海事大学，2011．

[5] 张琪．考虑作业干涉的多场桥存取箱优化问题研究[D]．大连：大连海事大学，2011．

[6] 乐美龙，林艳艳，范志强．基于两阶段启发式算法的多场桥作业调度研究[J]．武汉理工大学学报，2012，34(1)：60-65．

[7] 赵磊，胡志华，李淑琴．基于作业均衡的集装箱堆场箱区场桥作业调度[J]．武汉理工大学学报，2013，35(1)：69-74．

[8] 何军良，宓为建，严伟．基于爬山算法的集装箱堆场场桥调度[J]．上海海事大学学报，2007，28(4)：11-15．

[9] 严伟，宓为建，苌道方，等．一种基于最佳优先搜索算法的集装箱堆场场桥调度策略[J]．中国工程机械学报，2008，6(1)：95-100．

[10] Mak K L，Sun D．A new hybrid genetic algorithm and tabu search method for yard cranes scheduling with inter-crane interference[C] //Proceedings of the World Congress on Engineering 2009，London，U．K，2009：978-988．

[11] Javanshir H，Seyedalizadeh Ganji S R．Yard crane scheduling in port container terminals using genetic algorithm[J]．International Journal of Industrial Engineering，2010，6(11)：39-50．

[12] 刘志雄．调度问题中的粒子群优化方法及其应用研究[D]．武汉：武汉理工大学，2005．

YARD CRANES SCHEDULING OPTIMISATION BASED ON HYBRID EVOLUTIONARY STRATEGY ALGORITHM

Liu Zhixiong1Li Jun1Zhang Yu2Dong Jingwei3

1(SchoolofAutomobileandTrafficEngineering,WuhanUniversityofScienceandTechnology,Wuhan430081,Hubei,China)2(CollegeofLogisticsEngineering,WuhanUniversityofTechnology,Wuhan430063,Hubei,China)3(TianjinPortContainerTerminalCo.,Ltd.,Tianjin300456,China)

AbstractWe built the scheduling model and proposed a hybrid evolutionary strategy algorithm for the problem of container yard cranes scheduling.We adopted the real number-based four-dimension individual coding method,and designed the recombination operator,which is based on three-point crossover interchange,and the mutation operator which is based on two-point swap,as well as used three different local search strategies to optimise the performance of the algorithm.Through example analysis we proved the effectiveness of hybrid evolutionary strategy algorithm in optimising yard cranes scheduling problem.Among three different local search strategies,the local search strategy based on swap operation was better than the other two,it could obviously improve the optimisation performance of evolutionary strategy algorithm.At last,we analysed the local search times through a series of contrast tests.

KeywordsYard cranes schedulingEvolutionary strategy algorithmLocal search

收稿日期：2014-12-08。国家自然科学基金项目(70801047,71372202)；中央高校基本科研专项基金项目(2013-IV-057)。刘志雄，教授，主研领域：生产计划与调度、智能优化方法。李俊，硕士生。张煜，教授。东经伟，硕士生。

中图分类号TP3

文献标识码A

DOI:10.3969/j.issn.1000-386x.2016.05.061