可靠度理论在简支梁配筋选型中的应用

黄智

（湖南省郴州公路桥梁建设有限责任公司，湖南郴州 423000）



可靠度理论在简支梁配筋选型中的应用

黄智

（湖南省郴州公路桥梁建设有限责任公司，湖南郴州 423000）

摘要：针对钢筋砼结构材料性能不均匀、变异性大的特点，提出应用可靠度理论对简支梁配筋选型进行优化设计，并与规范计算方法进行比较。结果表明，运用可靠度理论计算方法得到的配筋方案能满足规范和设计要求，且比规范计算方法更接近实际情况和节省材料用量，将可靠度理论应用于结构配筋选型可行。

关键词：桥梁；简支梁；配筋选型；可靠度理论

可靠度理论在结构设计中运用极为广泛，也推动了结构设计理论迈向更高的台阶，一直以来都是结构优化设计的主要研究热点之一。结构设计过程中存在很多不确定因素，中国钢筋砼结构设计中规定的安全系数就曾因此进行了修改。很多设计人员在进行结构设计时不考虑可靠度理论，而是将其作为结构稳定性验算的分析方法，当可靠度分析结构不安全时，要再对结构设计方案进行定量化调整是非常困难的。

该文结合结构设计与可靠度分析构建受力模型，得到由抗力R和效应S组成的结构功能函数表达式，结合当量正态化法对结构进行配筋选型设计，将可靠度理论方法应用于结构设计中，依据规定的可靠指标，合理地改变材料的型号或材料的截面尺寸，对不满足规范要求的方案作出定量化调整。

1　结构功能函数的建立

针对矩形截面简支梁承受均布荷载条件下的受力状况，以正截面的抗弯为例进行分析。

1.1效应S表达式

简支梁受到均布荷载作用时，中心处产生最大弯矩。因此，将结构功能函数的效用S表示为该处的最大弯矩值M=ql2/8与结构安全系数K值的乘积，即S=KM（其中：l为梁的跨度，为已知量；q为荷载，为变量，存在标准差σq和均值μq）。

1.2抗力R表达式

如图1所示，依据结构设计规范和国外可靠度设计规范，正截面受弯构件的承载力为：

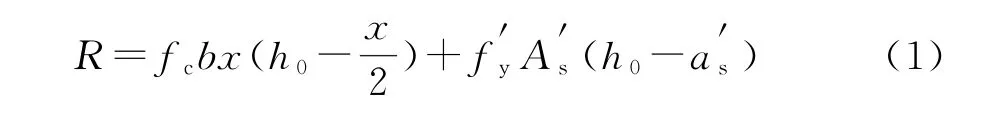
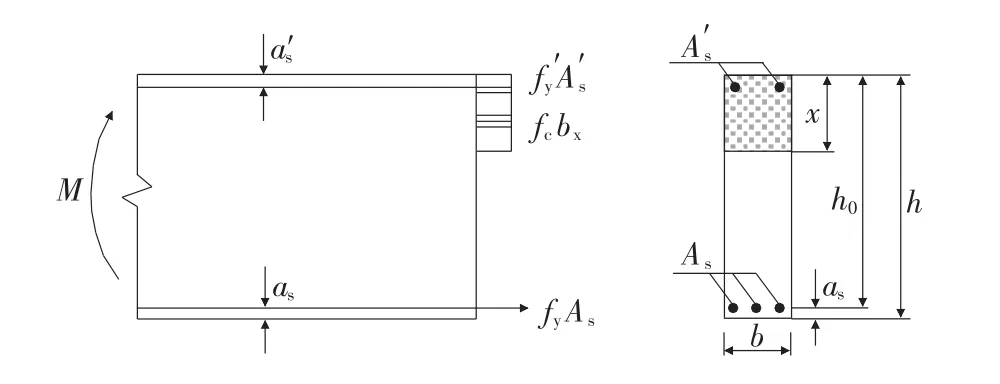
图1　正截面受弯构件的受力示意图

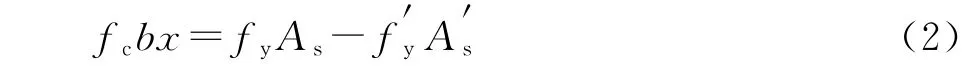
即使是相同型号规格的材料，也会因为各种因素而产生差别，故视为变量。σfy与分别为其标准差和均值。这些参数值主要通过室内砼轴心抗压强度试验及生产商提供的材料性能说明书确定。

1.3极限状态方程

通过式（1）和式（2）及简支梁的跨中弯矩值M计算得到结构的极限状态方程如下：

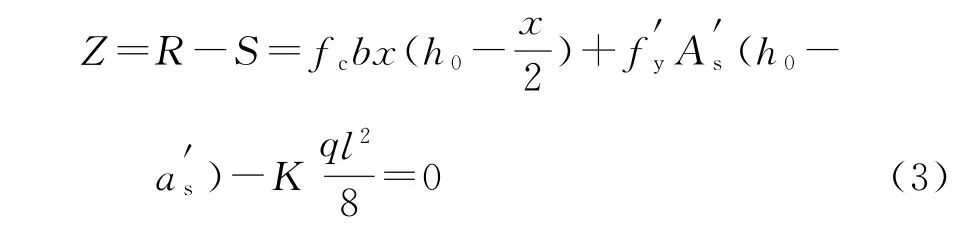
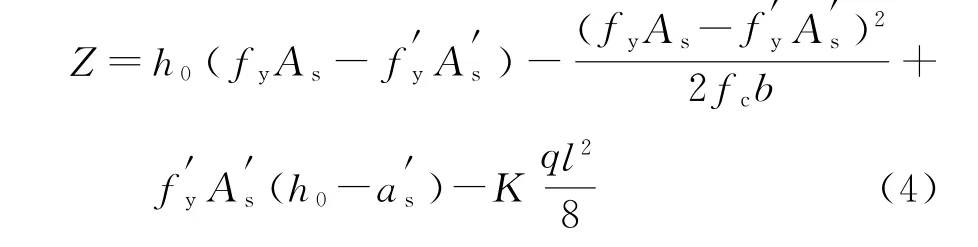
2　计算案例

梁的跨度l为6 m，主梁的截面尺寸为h×b= 480 mm×250 mm，受拉区边缘与受拉钢筋合力作用点之间的间距as为40 mm，受压区边缘与受压钢筋合力作用点之间的间距为40 mm。砼材料和钢筋的参数见表1。采用基于可靠度理论的方法进行配筋，要求可靠度指标β≥2.0。

2.1配筋计算

将上述参数代入式（4），得：

通过对验算点的迭代计算，得到不同方案。从中选取3种方案进行计算，设为已知，调整的大小。表2、表3为调整前后各方案的配筋计算结果。

表1　砼、钢筋材料的参数

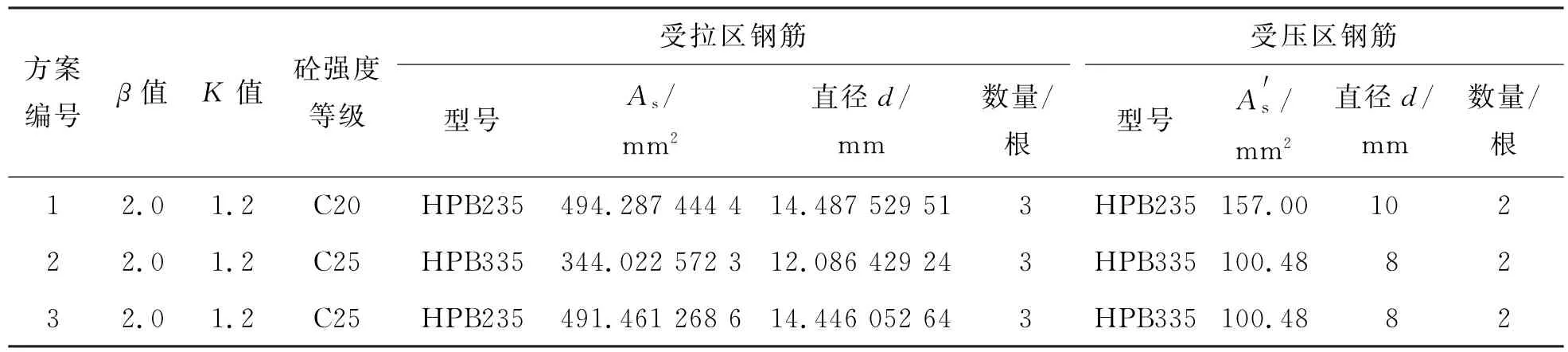
表2　3种方案配筋计算结果

表3　调整后3种方案配筋计算结果

2.2计算结果分析

2.2.1方案1

砼型号为C20，采用HPB235钢筋，受压区钢筋为2ϕ10，为157 mm2。根据可靠度指标β≥2.0的要求，得受拉区钢筋截面积As=494.287 444 4 mm2。通过调整，采用3ϕ16作为受拉钢筋。检验结果如下：

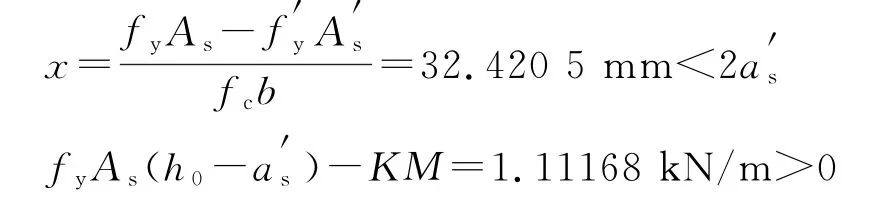
验算结果表明配筋结果满足设计要求。

2.2.2方案2

砼型号为C25，采用HPB335钢筋，受压区钢筋为2ϕ8，为100.48 mm2。根据可靠度指标β≥ 2.0的设计要求，计算得出受拉区钢筋截面积As= 344.022 572 3 mm2。通过调整，采用3ϕ14作为受拉钢筋。检验结果如下：

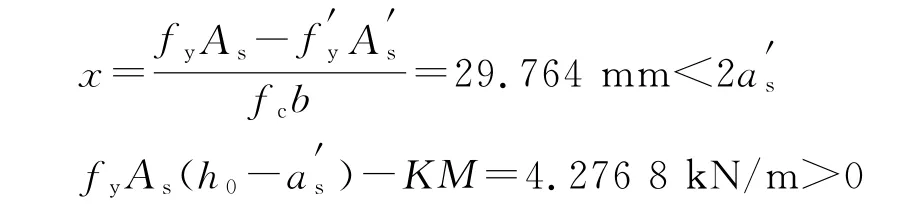
验算结果表明配筋结果满足设计要求。

2.2.3方案3

砼型号为C25，受拉区采用HPB235钢筋，受压区采用HPB335钢筋，受压区钢筋为3ϕ8，As为339.12 mm2。根据可靠度指标β≥2的要求，得出受拉区钢筋截面积=769.432 551 1 mm2。通过调整，采用3ϕ16作为受拉钢筋。检验结果如下：

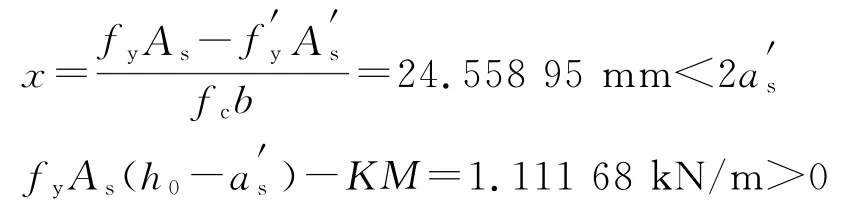
验算结果表明配筋结果满足设计要求。

3　与常规计算方法对比

常规计算法的表达式为：

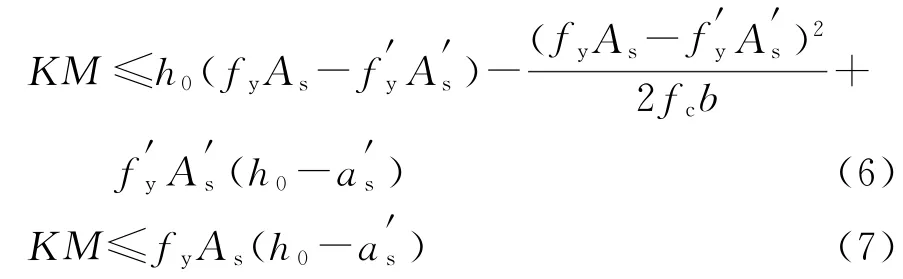
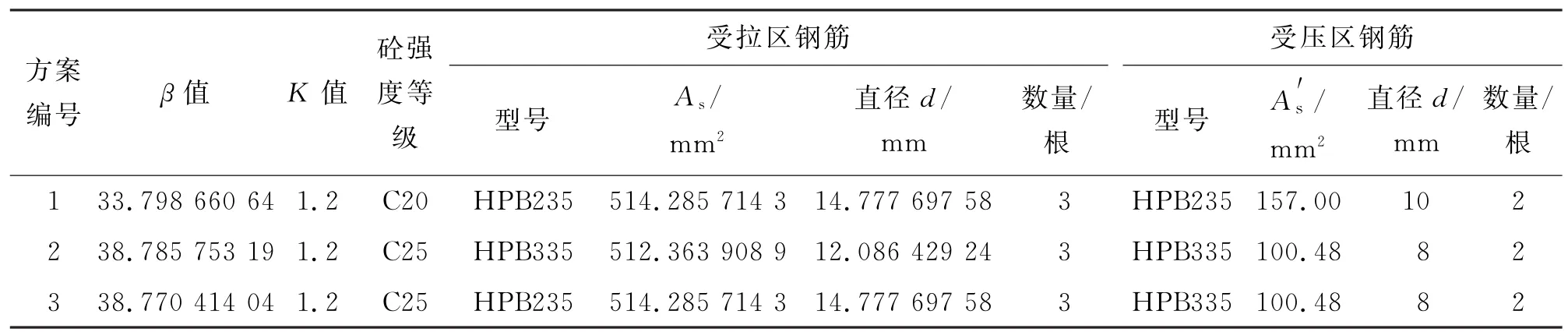
表4　常规方法配筋计算结果

对比表2和表4，可靠度理论和常规计算法得到的配筋结果均能满足设计规范的要求；常规方法通过改变结构承载力安全系数值保障结构的稳定性来进行配筋，结果偏于保守，可靠度指标β偏大；基于可靠度理论的方法通过预先设定结构需要满足的可靠度指标值来计算钢筋用量，相对于常规计算法节省材料用量3%～4%。

两种方法的计算流程对比见图2。

图2　配筋计算流程

4　结论

可靠度理论算法通过调整可靠度指标β和砼与钢筋的计算参数，得到不同设计组合方案，将各方案进行逐一计算，对比得到最优设计方案，设计结束后可不必进行可靠度评价。与常规计算方法的结果相比，该方法可在满足结构设计要求的前提下节省材料用量。该方法可为复杂结构设计提供参考。

参考文献：

［1］ 赵国藩，金伟良，贡金鑫.结构可靠度理论［M］.北京：中国建筑工业出版社，2000.

［2］ 李国强，黄宏伟，郑步全.工程结构荷载与可靠度设计原理［M］.北京：中国建筑工业出版社，2005.

［3］ 龙奴球，包世华.结构力学教程［M］.北京：高等教育出版社，1998.

［4］ ISO 2394-2015，General principles on reliability for structures［S］.

［5］ 苏怀智，刘红萍.高重力坝抗滑稳定安全度分析［J］.水利水电科技进展，2011（4）.

中图分类号：U448.21

文献标志码：A

文章编号：1671-2668（2016）03-0158-03

收稿日期：2015-10-20