新课标下提升数学教学有效性的探索
郭海燕


义务教育《数学课程标准》指出:“数学教学活动,特别是课堂教学应激发学生兴趣,调动学生积极性,引发学生的数学思考,鼓励学生的创造性思维;要注重培养学生良好的数学学习习惯,使学生掌握恰当的数学学习方法。”为落实这一理念,提升数学课堂教学有效性,笔者在新课程数学教学中对“如何激发学生的学习兴趣,引发学生数学思考,使学生掌握恰当的数学学习方法,培养学生的创新意识”作了有益的探索与尝试,收到了良好的教学效果。
一、创设有效的问题情境,激发学生的学习兴趣
古人云:“知之者不如好之者,好之者不如乐之者。”兴趣是学习的原动力,是学习的催化剂,它对学生的学习有着神奇的内驱动作用,能变无效为有效,化低效为高效。因此,数学教学必须把培养学生的学习兴趣放在首位。
【案例1】在教学苏科版八年级数学《生活中的不等式》时,可以设计如下学习情境:世纪公园的门票价是每人5元,若一次购票满30张,每张票可少收1元。某班有27名学生去世纪公园春游,当班长准备好零钱到售票处买27张票时,爱动脑筋的小李喊住了班长,提议买30张票。但有的同学不明白,明明我们只有27个人,买30张票,岂不是“浪费”吗?请你想一想,小李同学的提议对吗?并说说你的看法。这样,从学生原有的知识和生活经验出发,设置生活化的数学问题情境,提供学生思考的机会。而问题对学生而言是熟悉的、鲜活的、有生气的,有一定的挑战性,能激发学生的兴趣,唤起学生学习的积极性,有足够的吸引力,从而将学生引入到心欲通而不能、口欲讲而不会的境界。学生带着心理上的渴望,积极投入到新知识的学习中,这种学习是自发的、主动的,也是最有效的。
成功的数学教育无不是建立在学生对数学极大的兴趣基础之上的。教师应在研究教材与学生的基础上,对教学内容进行“二次加工”,结合具体内容创设必要的教学情境,利用有效的学习机制和教学手段,营造高效的学习氛围,彻底改变学生的学习状态,激发学生的学习欲望,实现学生由“苦学”“厌学”到“乐学”的转变。
二、精心设计问题,引发学生进行数学思考
《数学课程标准》向我们指出了“数学思考”这一方面课程目标希望达到的三个目的:让学生学会独立思考,体会数学思想,体会数学思维方式。数学思考是数学教学中最有价值的行为。我们在数学教学中要引导学生在学会知识的过程中学会思考,学会思考远比学会知识本身更重要。“学起于思,思起于疑”,问题是教学的心脏,是思维的起点,适切的问题容易激发学生的数学思考。
【案例2】“多边形内角和”教学(苏教版七年级)
问题1:我们已经知道,三角形的内角和等于180°,那么多边形的内角和等于多少呢?能否利用三角形的内角和定理推导出多边形的内角和?(引导性问题,无需学生立即回答)
问题2:数学研究中,如果一般的情形不容易解决的话,常常从特殊情形入手,我们知道长方形的内角和为360°,你能利用三角形内角和定理推导出这个结果吗?(由360°引导学生形成“剖”的思想:将长方形转化为两个三角形)
问题3:是否任意一个四边形的内角和都是360°?为什么?
问题4:根据上述思路,你能推导出五边形的内角和吗?六边形、七边形呢?n边形呢?(同时完成表格,表格分多边形的边数、分成的三角形个数、多边形的内角和三栏)
问题5:将多边形“剖”成三角形还有哪些“剖”法?请利用你的“剖”法求出n边形的内角和。
该问题串按照“从特殊到一般”的研究思路,按“矩形一般四边形—五边形、六边形、七边形—n边形”的顺序,引导学生逐步深入得出结论,这里的关键是“剖”的思想的形成。问题设计重在引导学生自己探究发现,而不是直接教给学生,渗透了化归、转化的数学思想,最后问题5对学生进行发散思维训练,寻找不同的“剖”法和推导思路。
事实上,数学知识的形成往往与学生的思考、探索等活动融合在一起。因此,在数学教学中,教师一定要引导学生经历数学知识形成与发展过程,不可错失培养学生数学思考的良机。
三、设计试验操作,使学生掌握恰当的学习方法
《数学课程标准》论述学习方式时指出:“学生应当有足够的时间和空间经历观察、实验、猜测、计算、推理、验证等活动过程。”学习数学的最好方法是做数学,有些数学知识可通过引导学生自己亲自操作、实验或通过现代教育技术手段演示及操作,让学生以“再发现”和“再创造”的方式经历数学知识的发生发展过程,在这个过程中,学生能容易地自己发现、掌握知识,形成技能,并获得对这些知识所蕴含的基本数学思想的感悟、对基本活动经验的积累,以及获得积极向上的情感体验。
【案例3】确定圆的条件探索
对于“不在同一条直线上的三个点确定一个圆”这一知识点,我们可以引导学生通过实验操作获得,具体操作要求如下:
(1)在纸上作出一个点A,经过点A作圆。你能作出多少个?
(2)在纸上作出两个点A与B,经过点A、B作圆。你能作出多少个?这些圆的圆心在哪里?
(3)在纸上作出三个点A、B、C。如果A、B、C三点不在同一直线上,那么经过这三点能作出一个圆吗?如果能,怎样作出经过这三点的圆?经过这三点的圆的圆心在哪里?经过这三点可以作出多少个圆?
学生在动手操作(1)时得到的结论是经过一个点可以作出无数个圆,如图1所示。
学生在动手操作(2)时得到的结论是经过两个点可以作出无数个圆,如图2所示,这些圆的圆心在同一条直线上(图2中的虚线所在的直线)。这条直线就是过已知两点构成的线段的垂直平分线,发现这一点非常重要,为解决问题(3)做了铺垫。
学生在研究第(3)个问题时,可能有一定的困难,教师可用下面的问题进行提示引导:
师:假如经过三点A、B、C的圆已经作出,则圆心O到A、B、C三点的距离是怎样的?
生:相等。
师:到A、B两点的距离相等的点在哪里?
生:在线段AB的垂直平方线上。
师:到B、C两点距离相等的点在哪里?
生:在线段BC的垂直平方线上。
师:怎样确定经过A、B、C三点的圆的圆心?
生:先作出线段AB的垂直平分线,再作出线段BC的垂直平分线,其交点就是圆心。……
至此,学生已经能独立作出经过A,B,C三点的圆来,而且发现这个圆是唯一的,如图3所示。
这样的实验过程恰好经历了确定圆的条件的探索过程,学生在探究的过程中除了能获取知识、发展技能、形成能力外,还能受到科学价值观和科学方法的教育,并发展自己的个性。
四、实施探究式教学,培养学生的创新意识
“创新意识”是《数学课程标准》提出的十个核心概念之一。关于创新意识的培养问题,在过去的十余年里人们讨论得比较多,也积累了一些好的方法。如实施探究式的教学方法就是一例。在这种教学模式中,因为它的条件不完备、答案不确定且具有层次性,解决策略具有发散性和创新性等特征,容易使学生主动参与、主动探索,也可以让不同层次的学生在同一问题上得到不同的发展,从而让学生都有体验成功的机会,在成功的基础上探索更深层次的问题,形成良好的思维品质,培养创新思维。
【案例4】“相似三角形”复习
问题1:如图4,D、E分别在△ABC的边AB、AC上,当满足什么条件时,△ADE与△ABC相似?(让学生从角与边两个方面考虑添加条件)
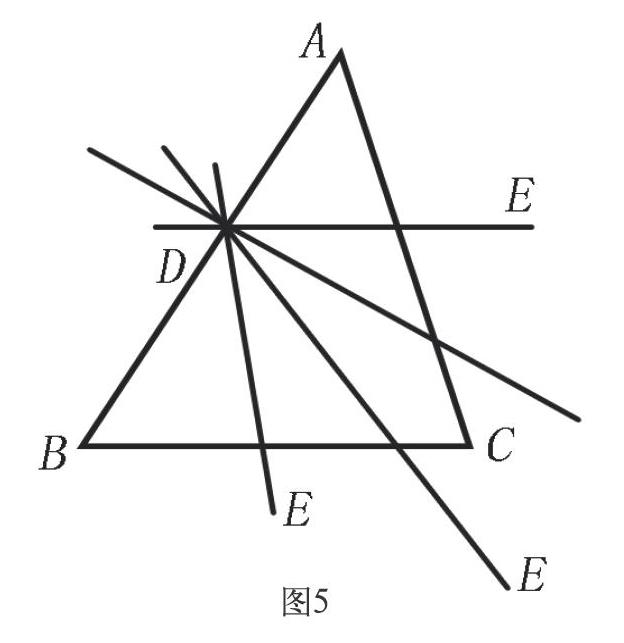
问题2:如图5,在△ABC中,D是AB边上一点,过点D作一条直线DE交另一边与E,使所得三角形与原三角形相似,共有几种方法,请试一试。
由于开放性问题答案不唯一,学生有了创新的空间,在寻求多种答案的过程中,全体学生认真思考,动手实践,参与讨论,集思广益,互相启发,分享智慧,最终获得如图的四种方法。这样既加深了学生对所复习内容的理解,又调动了学生的积极性,既提高了学生发散思维与求异思维的能力,发展了其创造性思维,又培养了学生钻研问题的习惯与能力。
总之,新课程改革理念主导下的有效教学是一个开放性的、探索性的动态过程,没有最好,只有更好。因此,我们要加强理论学习和研究,不断探索出提高教学有效性的新途径。

