考虑鼓胀变形的散体材料桩复合地基沉降计算

张玲+赵明华

摘 要：针对竖向荷载作用下靠近桩顶一定深度的范围内，桩体不仅会发生竖向压缩变形且会发生侧向鼓胀变形特性，基于荷载传递法，导出了竖向荷载作用下散体材料桩复合地基中的某根单桩的桩身压缩量计算公式，进而得到新的散体材料桩复合地基沉降计算公式.分析时，视散体材料桩为弹性均质体，根据广义胡克定律得到其应力应变关系；桩周土提供的侧向约束力为桩侧竖向力引起的侧向土压力，并考虑加筋垫层的侧向约束作用及其沿深度的传递对桩体侧向约束的有利影响.为验证本文方法的可行性，对某一工程实例进行分析，且与其它方法进行比较分析.结果表明：与常规计算方法相比，本文方法从荷载传递规律出发，可考虑鼓胀深度随桩顶竖向荷载的增加逐渐向深处发展的特点，更符合散体材料桩复合地基的实际受力变形状况.

关键词：复合地基；散体材料桩；沉降；荷载传递；鼓胀变形

中图分类号：U416.1 文献标识码：A

文章编号：1674-2974（2016）05-0120-05

Abstract：The granular material pile has its own deformation characteristics under vertical loads. The granular material pile shows not only a vertical compressive deformation but also a radial expansion near the top of the pile. According to the study of this load transfer mechanism， a new equation was developed to calculate the compressive deformation of a single granular material pile. On the basis of this investigation way， a new method to predict the settlement of the composite foundation reinforced by granular material piles such as stone columns was developed. In the analysis model， the granular pile was treated as an elastic material satisfying Hooke's law， and the lateral confining support provided by the surrounding soil was assumed as lateral soil pressure. Further， the beneficial influence of the lateral restraint of the reinforced cushion as well as its development within depth on restricting the lateral bulging of the granular pile was taken into account. Finally， a case study was performed to validate the proposed method. The foundation settlements predicted by the proposed model were close to those of existing calculation methods. The prediction results indicate that the proposed method based on the load transfer mechanism is more practical because the proposed method can consider the variation law that the depth of lateral deformation of the pile increases with the increase of the vertical load acting on the top of the pile.

Key words：composite foundation；granular material pile；settlement；load transfer；lateral bulging

以碎石桩为代表的散体材料桩及其与桩间土形成的复合地基已广泛地应用于地基加固工程.沉降计算是该复合地基设计理论的重要组成部分.尤其是复合地基按沉降控制设计时，沉降计算更为重要.有关散体材料桩复合地基的沉降计算国内外学者提出了理论或经验计算公式.其中较为常用的方法是采用复合模量法计算加固区的压缩量，再采用分层总和法计算下卧层的压缩量，进而得到整个复合地基的沉降量[1-3].该方法的假定之一是竖向荷载作用下桩与桩间土之间无侧向挤压作用，各自都不发生侧向变形[4].

然而，当桩体材料及桩周土条件不变时，桩体鼓胀变形应随桩顶竖向荷载的增加而逐渐向深处发展.故本文从散体材料桩的荷载传递机理出发，考虑鼓胀变形随荷载变化，提出一种计算散体材料桩桩身压缩量的新方法，进而获得散体材料桩复合地基的沉降量.

1 复合地基沉降计算新方法

1.1 桩、土受力变形分析

取散体材料桩复合地基中的某根单桩进行分析，桩顶作用荷载qp，桩间土作用荷载qs，qs=qp/n，其中n为桩土应力比.对于散体材料桩复合地基，在无测试资料时，对黏性土可取2～4，粉土和砂土n可取1.5～3.0.原地基土强度低者取大值，反之取小值[6].若复合地基上作用荷载为q，则qp=n1+（n-1）mq，m为复合地基置换率.为便于分析，沿桩长将桩划分为N段（图1）.并取其中第i段进行分析（图2）.

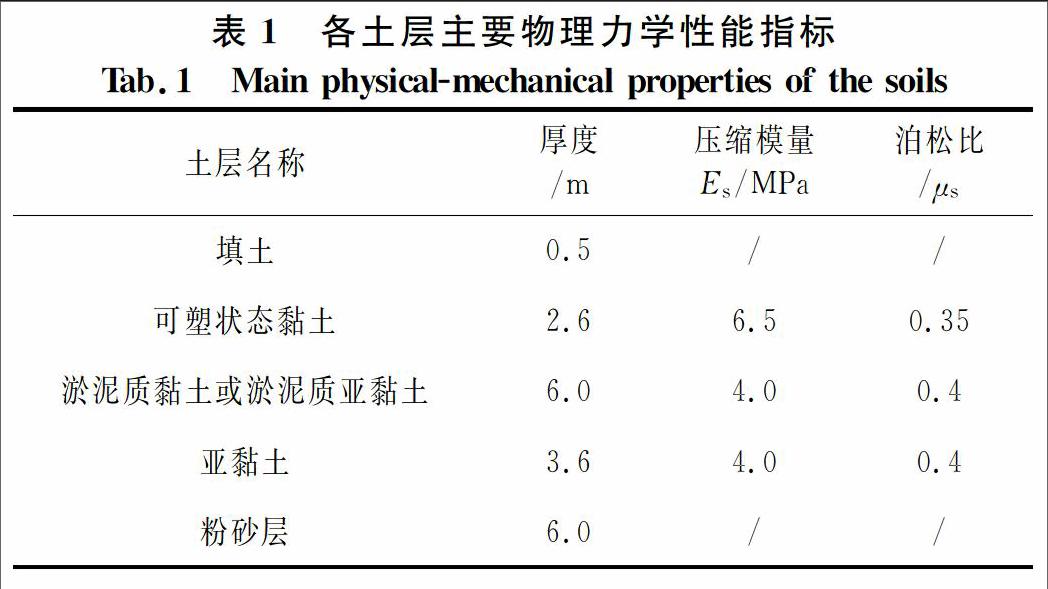
由前述推导可知，本文方法计算散体材料桩复合地基沉降时，桩土应力比需作为一已知参数，然而准确确定桩土应力比非常困难，盛崇文建议[2]对于该工程当设计荷载小于60 kPa时桩土应力比取3～5；大于60 kPa时取2～4.当沉降计算荷载为60 kPa时，已有文献[2，7-8]中桩土应力取值有两种情况n=3[7-8]和n=4[2]，为便于与其它文献计算结果对比分析，故本文方法计算沉降时，计算荷载亦取60 kPa，而桩土应力比取n=3和n=4分别加以计算.

本文方法计算时取桩土应力比n=3，经计算得整个桩身压缩量sp=28.9 mm，其中鼓胀段的压缩量为7.4 mm，非鼓胀段的压缩量为21.5 mm；鼓胀深度hb=0.9 m；下卧层压缩量ss=12.0mm；故整个碎石桩复合地基的沉降量为s=40.9 mm.若取n=4，得hb=1.6m；sp=40.2 mm；ss=12.0 mm；s=52.2 mm.

与其它方法计算结果的比较见表2.其中，盛崇文[2]是采用复合模量法计算加固区的压缩量，复合模量按式Esp=[1+（n-1）m]Es计算；邓修甫等[7]是将碎石桩简化成等体积墙体，再根据碎石桩与桩间土的变形协调作用分鼓胀段与非鼓胀段两部分计算加固区的压缩量；基于邓修甫等的计算方法，孙林娜等[8]将基桩与桩间土的相互作用视为空间问题来计算复合地基加固区的压缩量；各方法下卧层的压缩量均采用分层总和法得到.

由表2可见，采用复合模量法计算桩身压缩量较其它方法的计算结果偏大；邓修甫等方法[7]将复合地基沉降计算简化成平面问题，强化了桩体作用，所得的复合地基沉降量偏小；孙林娜等方法[8]计算复合地基沉降时，碎石桩的鼓胀深度为桩体极限受荷状态下的鼓胀变形深度，其中鼓胀段压缩量较本文方法（n=3）偏大，非鼓胀段压缩量因非鼓胀段长度减小而较本文方法（n=3）偏小；且孙林娜等方法[8]因夸大了实际工作荷载作用下侧向鼓胀变形对复合地基沉降的影响，使得整个桩身压缩量较本文方法偏大.而本文方法采用静止土压力计算桩周土提供的侧向约束力偏小，变形量略为偏大，但可反映碎石桩鼓胀变形随荷载发展变化的实际情况.

3 结 论

1） 基于桩体受荷发生竖向压缩变形及侧向鼓胀变形的特性，提出一新的散体材料桩复合地基加固区压缩量计算公式，进而可得整个复合地基的沉降量.

2） 与常规计算方法相比，本文方法从荷载传递规律出发，更符合散体材料桩复合地基的实际受力变形状况.

3） 利用本文方法对某一具体工程实例进行了计算，经与其它方法及实测值的比较分析，本文所得结果具有其合理性.

4） 本文方法计算散体材料桩复合地基沉降时，桩土应力比需是已知参数，而桩土应力比对复合地基沉降有一定程度影响，实际设计中如何正确合理的选取散体材料桩复合地基桩土应力比仍有待进一步的深入研究.

参考文献

[1] 龚晓南.复合地基理论及工程应用[M].北京：中国建筑工业出版社，2002：150-169.

[2] 盛崇文.碎石桩复合地基的沉降计算[J].土木工程学报，1986，19（l）：72-80.

[3] 曹文贵， 唐旖旎， 王江营. 基于孔隙介质模型的散体材料桩复合地基沉降分层总和分析方法[J]. 湖南大学学报：自然科学版， 2014，41（11）：87-95.

[4] 张定. 碎石桩复合地基的作用机理分析及沉降计算[J]. 岩土力学， 1999， 20（2）：81-86.

[5] 张定. 散体材料桩复合地基的沉降分析与计算[J]. 铁道学报，1998，20（6）：98-104.

[6] 龚晓南.复合地基设计和施工指南[M].北京：人民交通出版社，2003：109-110.

[7] 邓修甫，刘新华，张琳.碎石桩复合地基沉降计算方法[J].湘潭矿业学院学报，2003，18 （4）：55 -57.

[8]孙林娜，龚晓南. 散体材料桩复合地基沉降计算方法的研究[J]. 岩土力学， 2008，29（3）：846-848.

[9] B.A.弗洛林.土力学原理（第一卷）[M] 徐志英，译. 北京：中国建筑工业出版社， 1973：87-88.

[10]饶为国. 桩-网复合地基原理及实践[M]. 北京：中国水利水电出版社， 2004：30-50.