耦合复Ginzburg-Landau方程中的相-模螺旋结构相似性
高继华,史文茂,张 超,戈早川,杨海涛
深圳大学材料学院,深圳市特种功能材料重点实验室,广东深圳518060
耦合复Ginzburg-Landau方程中的相-模螺旋结构相似性
高继华,史文茂,张超,戈早川,杨海涛
深圳大学材料学院,深圳市特种功能材料重点实验室,广东深圳518060
摘要:以二维复Ginzburg-Landau方程为模型,研究单向耦合时空系统中的斑图动力学行为.以稳定的模螺旋波为驱动系统,讨论响应系统在不同耦合强度下的时空斑图动力学行为.通过同步函数与系统相-模频率分析发现,在弱耦合强度条件下,驱动系统的相与响应系统的模会在螺旋结构上出现相似性.分别用靶波与平面波作驱动系统,发现同样现象.研究结果证明,随着耦合强度的增大,单向耦合复Ginzburg-Landau方程系统的耦合行为遵循从非同步、相与模螺旋结构上的相似到完全同步的过程.该现象同时解释了模螺旋波的产生.
关键词:微分动力系统;时空系统;斑图;复Ginzburg-Landau方程;单向耦合;螺旋结构;模螺旋波
在自然界中,相互耦合的系统可以产生丰富的动力学行为,包括不同模式之间的同步和竞争行为.双层系统能展现许多单层系统所没有的现象,可以作为许多三维薄层结构的近似,例如血管、心脏中心室与心房的内壁等.早期时空系统间的耦合研究基本局限于耦合映像格子、多振子系统和一维复Ginzburg-Landau 方程(complex Ginzburg-Landau equation, CGLE)模型[1].Bargard等[2-5]通过一维CGLE中2个不同参数系统的对称耦合及非对称耦合研究时空混沌的同步行为.Junge等[6]将相湍流与缺陷湍流进行耦合,在耦合强度较大时使两者实现了相同步.随着计算机技术的发展,时空斑图的耦合动力学研究逐渐展开.在双层耦合振荡系统中呈现出“twinkling eyes”等丰富多彩的图灵斑图[7-9];在实验中也观察到了时空斑图的同步现象[10-12];袁国勇等[13-15]以FitzHugh-Nagumo方程为模型,通过耦合观察到螺旋波同步、多螺旋波同步、螺旋波消失与失同步等现象;Yang等[16]在耦合Bar模型中观察到了螺旋波的漫游及同步行为;Gao等[17]发现双层耦合复CGLE系统在一定的耦合强度与初始条件下可形成稳定的模螺旋波.由于模螺旋波具有许多新颖的性质,模螺旋波的产生的条件及其稳定性已有大量研究[18-19],但其产生的机理仍未见得证.近两年,基于CGLE的耦合与同步行为的研究受到大量关注[20-22].受模螺旋波研究的启发,本研究基于CGLE模型,以稳定的模螺旋波为驱动系统与响应系统进行耦合,研究单向耦合系统的斑图动力学行为,响应系统的初始条件为多螺旋波,讨论在不同耦合强度条件下,响应系统的动力学行为与耦合强度之间的关系.研究发现,在相对较弱的耦合强度下,存在驱动系统的相与响应系统的模在螺旋结构上相似的现象,并根据系统同步情况与频率情况找到了这一现象的特点.然后以同样的方法,分别以靶波与平面波作为驱动系统来观察响应系统的动力学行为与耦合强度之间的关系,印证了此现象的一般规律性.同时,此现象本身也说明了为什么会有模螺旋波的出现.
1模型
CGLE是常见的反应扩散系统模型之一,它描述了系统在Hopf分岔点附近的动力学行为,是显示非线性波动和相变现象的重要物理模型.CGLE具有极丰富的动力学行为[23-28].耦合CGLE模型为
∂tA1=A1+(1+iα)2A1-
(1)
∂tA2=A2+(1+iα)2A2-
(2)
其中, A1和A2是系统变量,为复数;考虑二维时空系统,2=∂2/∂x2+∂2/∂y2; 实数α和β为系统参数; A1为驱动系统; A2为响应系统; ε为系统之间的负反馈耦合强度.
系统尺寸L=128, 空间步长h=1, 时间步长τ=0.04, 采用无流边界条件(no flux boundary condition).驱动系统和响应系统的参数相同, α=-1.34, β=0.35. 采用欧拉方法求解.在非耦合的情况下,驱动系统和响应系统均可产生稳定的螺旋波.为使响应系统具有一般代表性,初始条件设为多螺旋波.在之前的耦合CGLE系统研究中,以相螺旋波做驱动系统,去驱动多螺旋波,在弱耦合的条件下发现响应系统的模与驱动系统的相具有螺旋结构上的相似性,可生成模螺旋波[17],如图1.

图1 ε=0.08,t=800时驱动系统与响应系统相与模的时空图Fig.1 Phase-amplitude spatiotemporal pattern of the drive system and the response system at ε=0.08 and t=800
为更准确地对比两系统之间的差异,引入同步函数
(3)
其中, T为系统的演化总时间; L为系统尺寸; t为时间变量; x和y为系统的空间坐标.
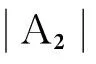
2数值模拟
以模螺旋波作为驱动系统,研究响应系统的动力学行为,观察在弱耦合条件下响应系统的模与驱动系统的相是否会出现螺旋结构上相似的现象.使用如式(1)和式(2)的耦合CGLE模型,取ε=0.08以确保系统A2产生稳定的模螺旋波.在此基础上,引入响应系统A3, 即
∂tA3=A3+(1+iα)2A3-
(4)
A3的初始条件为多螺旋波,在不同的耦合强度ε1下观察响应系统A3的模的斑图变化情况,结果如图2.其中, ε1的取值从0逐步增加,直到能使两系统趋于同步.

图2 驱动系统为稳定的模螺旋波,响应系统初始条件为多螺旋波时,不同耦合强度ε1下响应系统模的时空斑图Fig.2 Amplitude spatiotemporal pattern of the response system driven by the stable amplitude spiral wave with different ε1 and the multi-spiral wave as the initial condition of response system
由图2可见,在ε1较小的情况下, A3模的斑图中存在缺陷点,但初始的多螺旋波受影响不大.随着ε1的增大,系统中的缺陷点逐渐消失.当ε1足够大时,系统A2与系统A3趋于完全同步,形成模螺旋波.
下面讨论同步函数值随ε1的变化情况.如图3,同步函数值随着ε1的增大明显分为3个区域:当ε1<0.026时,同步函数P的值较小,对应着A3的状态为多螺旋波;当0.026<ε1<0.041时,同步函数P的值较大,出现一个稳定的平台,这与文献[17]图4(b)中AS区域所示类似, A3模的斑图也较为特殊(见本文图2中ε1=0.027、 0.030、 0.033、 0.036、 0.039时响应系统模的时空斑图),这是一个值得注意的现象;当ε1>0.041时,同步函数P的值骤降到趋于0, A3与A2基本同步,此时A3的状态为模螺旋波.

图3 同步函数随耦合强度的变化情况,驱动系统为模螺旋波,响应系统初始条件为多螺旋波Fig.3 The dependence of P on ε1 with the system driven by the stable amplitude spiral wave and the multi-spiral wave as the initial condition of response system
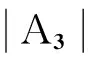

图4 ε1=0.033,t=4 100时驱动系统与响应系统相与模的时空斑图Fig.4 Phase-amplitude spatiotemporal pattern of thedrive system and the response system at ε1=0.033 and t=4 100
通过以上分析,可得出结论,认为耦合CGLE系统产生模螺旋并非偶然现象,而是遵循一定的规律:单向耦合系统的同步遵循从非同步、相与模螺旋结构的相似到完全同步的过程.
为证明此结论在其他波形中也同样适用,改用靶波做驱动系统,来观察响应系统的动力学行为.使用如式(1)和式(2)的耦合CGLE模型,在驱动系统A1的局部(系统格点中心5×5区域)加入振荡项sin(ωt)(靶波源),使驱动系统产生稳定的靶波, ω取值0.03,响应系统的初始条件为多螺旋波.其同步函数值随耦合强度变化如图6.当ε<0.034时,驱动系统对响应的影响不大,响应系统仍表现为多螺旋波;当0.034<ε<0.162时,响应系统出现了模靶波,出现驱动系统的相与响应系统的模螺旋结构相似的现象(如图7),其同步函数值稳定光滑过渡;当ε>0.162时,同步函数值快速趋于零,两系统趋于同步,响应系统逐步演化为相靶波.再来观察ε=0.050时系统的时序及频率(如图8),由于驱动系统受靶波源振荡参数ω的影响,运动发生周期性变化,由单周期运动变为多周期运动,如图8(a)所示,系统的主频率Ω1=0.005 68 Hz(与靶波源振荡频率ω/(2π)相近),由于耦合强度较弱,响应系统的频率受影响不大,主频率Ω2=0.052 06 Hz,响应系统的模的频率为0.046 51Hz≈Ω2-Ω1, 这与本研究发现的规律相符,证明了本研究的结论.为验证结论的可靠性,通过在实验中选取大量不同的可以使系统产生靶波的ω值,来研究其耦合行为,结果发现了相同的规律性,这里不再一一列出.

图5 ε1=0.033时驱动系统与响应系统的时序与频率图Fig.5 Timing diagram and frequency diagram of the drive system and the response system at ε1=0.033
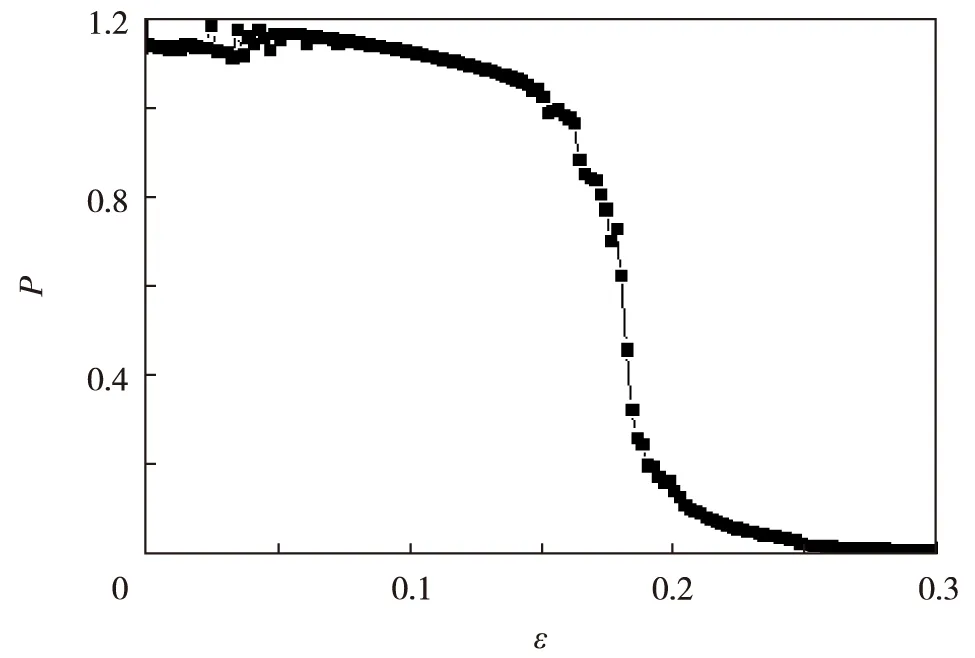
图6 同步函数随耦合强度的变化情况,驱动系统为靶波, 响应系统初始条件为多螺旋波 Fig.6 The dependence of P on ε with the system driven by the stable target wave and the multi-spiral wave as the initial condition of response system
以上耦合CGLE系统实验,不管是用螺旋波作为驱动系统,还是靶波作为驱动系统,研究的都是波的中心区域的动力学行为.为验证远离波的中心区域的耦合动力学行为符合同样的规律,本研究改用平面波作驱动系统,以同样方法观察响应系统的变化情况.选驱动系统为如式(5)的平面波

图7 ε=0.050,t=1 900时驱动系统与响应系统相与模的时空斑图Fig.7 Phase-amplitude spatiotemporal pattern of the drive system and the response system at ε=0.050 and t=1 900
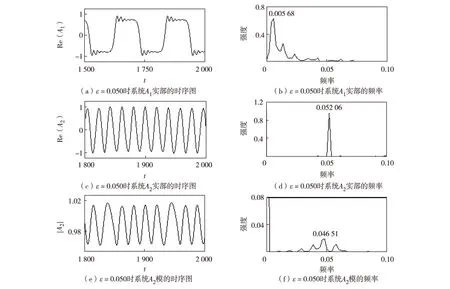
图8 ε=0.050时驱动系统与响应系统的时序与频率图Fig.8 Timing diagram and frequency diagram of the drive system and the response system at ε=0.050
(5)

图9 同步函数随耦合强度的变化情况,驱动系统为平面波,响应系统初始条件为多螺旋波Fig.9 The dependence of P on ε with the system diven a plane wave and the multi-spiral wave as the initial condition of response system


图10 ε=0.080,t=1 800时驱动系统与响应系统相与模的时空斑图Fig.10 Phase-amplitude spatiotemporal pattern of the drive system and the response system at ε=0.080 and t=1 800
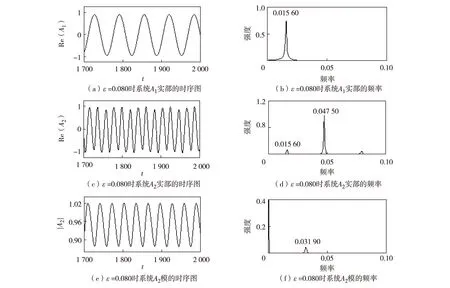
图11 ε=0.080时驱动系统与响应系统的时序与频率图Fig.11 Timing diagram and frequency diagram of the drive system and the response system at ε=0.080
结语
双向耦合的两个系统的动力学行为与相互之间的耦合强度有着很大的关系,其动力学行为也极为复杂.我们可以通过单向耦合来近似的研究双向耦合系统中一方耦合强度较弱时的动力学行为规律.本研究基于CGLE模型研究了单向耦合系统的斑图动力学行为,观察了在模螺旋波驱动下,响应系统在不同耦合强度下的斑图动力学行为.通过斑图结构的相似性确认了在弱耦合(非同步)与强耦合(完全同步)之间,存在驱动系统的相与响应系统的模在螺旋结构上相似的现象.通过同步函数分析与系统相-模频率分析找到了这一现象的特点.最后用不同的波形做驱动确认了这种现象的一般规律.也就是说,单向耦合CGLE方程系统的同步遵循从非同步、相-模斑图螺旋结构的相似到完全同步的过程,这也同时解释了模螺旋波产生的原因.该发现的新颖性和潜在的应用方向在于找到一种用较小的代价(弱耦合)来实现混沌控制(相-模螺旋结构的相似性)的方法.
参考文献/References:
[1] Amengual A, Garcia E H, Montange R, et al. Synchronization of spatiotemporal chaos: the regime of coupled spatiotemporal intermittency[J]. Physical Review Letters, 1997, 78(23): 4379-4382.
[2] Bragard J, Boccaletti S, Mendoza C, et al. Synchronization of spatially extended chaotic systems in the presence of asymmetric coupling[J]. Physical Review E, 2004, 70(3): 36219-36227.
[3] Bragard J, Boccaletti S, Mancini H. Asymmetric coupling effects in the synchronization of spatially extended chaotic systems[J]. Physical Review Letters, 2003, 91(6): 64103-64106.
[4] Bragard J, Arecchi F T, Boccaletti S. Characterization of synchronized spatiotemporal states in coupled nonidentical complex Ginzburg-Landau equations[J]. International Journal of Bifurcation and Chaos, 2000, 10(10): 2381-2389.
[5] Boccaletti S, Bragard J, Arecchi F T, et al. Synchronization in nonidentical extended systems[J]. Physical Review Letters, 1999, 83(3): 536-539.
[6] Junge L, Parlitz U. Phase synchronization of coupled Ginzburg-Landau equations[J]. Physical Review E, 2000, 62(1): 438-441.
[7] Yang L, Zhabotinsky A M, Epstein I R. Stable squares and other oscillatory turing patterns in a reaction-diffusion model[J]. Physical Review Letters, 2004, 92(19): 198303-198306.
[8] Yang L, Epstein I R. Oscillatory turing patterns in reaction-diffusion systems with two coupled layers[J]. Physical Review Letters, 2003, 90(17): 178303-178306.
[9] Yang L, Epstein I R. Symmetric, asymmetric, and antiphase turing patterns in a model system with two identical coupled layers[J]. Physical Review E, 2004, 69(2): 26211-26216.
[10] Winston D, Arora M, Maselko J, et al. Cross-membrane coupling of chemical spatiotemporal patterns[J]. Nature, 1991, 351: 132-135.
[11] Neubecker R,Utlich B G. Experimental synchronization of spatiotemporal disorder[J]. Physical Review Letters,2004, 92(15): 154101-154104.
[12] Hildebrand M, Cui J X, Mihaliuk E, et al. Synchronization of spatiotemporal patterns in locally coupled excitable media[J]. Physical Review E,2003,68(2):26205-26208.
[13] 袁国勇,杨世平,王光瑞,等.两个延迟耦合Fitz Hugh-Nagumo系统的动力学行为[J].物理学报, 2005,54(4):1510-1522.
Yuan Guoyong, Yang Shiping, Wang guangrui, et al. Dynamics of two FitzHugh-Nagumo systems with delayed coupling[J]. Acta Physica Science, 2005,54(4):1510-1522.(in Chinese)
[14] Yuan Guoyong,Zhang Guangcai,Wang Guangrui, et al. Synchronization and asynchronization in two coupled excitable systems[J]. Communications in Theoretical Physics,2005,43(3):459-465.
[15] Yuan Guoyong, Yang Shiping, Wang Guangrui, et al. Segmented spiral waves and anti-phase synchronization in a model system with two identical time-delayed coupled layers[J]. Communications in Theoretical Physics, 2008, 49(1): 174-180.
[16] Yang Hujiang, Yang Junzhong. Spiral waves in linearly coupled reaction-diffusion systems[J]. Physical Review E, 2007, 76(1): 16206-16213.
[17] Gao Jihua, Xie Lingling,Nie Haichun,et al. Novel type of amplitude spiral wave in a two-layer system[J]. Chaos, 2010,20(4):043132.
[18] 高继华,谢伟苗,高加振,等.复金兹堡朗道方程中的模螺旋波[J].物理学报,2012,61(13):120506.
Gao Jihua, Xie Weimiao, Gao Jiazhen, et al. Amplitude spiral wave in coupled complex Ginzburg-Laudau equation[J]. Acta Physica Science,2012,61(13):120506.(in Chinese)
[19] 高继华,王宇,张超,等.复Ginzburg-Landau方程中模螺旋波的稳定性研究[J].物理学报,2014,63(2):020503.
Gao Jihua, Wang Yu, Zhang Chao, et al. Stability for amplitude spiral wave in complex Ginzburg-Landau equation[J]. Acta Physica Science,2014, 63(2): 020503.(in Chinese)
[20] Schmidt L, Krischer K. Clustering as a prerequisite for chimera states in globally coupled systems[J]. Physical Review Letters, 2015, 114(3): 034101.
[21] Haugland S W, Schmidt L, Krischer K. Self-organized alternating chimera states in oscillatory media[J]. Scientific Reports, 2015, 10(5): 9883
[22] Ciszak M, Mayol C, Mirasso C R, et al. Anticiapted synchronization in coupled complex Ginzburg-Landau systems[J].Statistical Mechanics, 2015, 92(3): 032911.
[23] Mikhailov A S, Showalter K. Control of waves, patterns and turbulence in chemical systems[J]. Physics Reports, 2006, 425(2/3): 79-194.
[24] Goryachev A, Kapral R. Structure of complex-periodic and chaotic media with spiral waves[J]. Physical Review E, 1996, 54(5): 5469-5481.
[25] Kuramoto Y. Chemical oscillations, waves and turbulence[M]. New York: Springer,1984.
[26] Cross M, Hohenberg P. Pattern formation outside of equilibrium[J]. Reviews of Modern Physics, 1993, 65(3): 851-1112.
[27] Aranson I S, Kramer L. The world of complex Ginzburg-Landau equation[J]. Reviews of Modern Physics, 2002, 74(1): 99-143.
[28] Hendrey M, Nam K, Guzdar P, Ott E, Target waves in the complex Ginzburg-Landau equation[J]. Physical Review E, 2000, 62(6): 7627-7631.
【中文责编:英子;英文责编:子兰】
Similarity of spiral structures between phase andamplitude in coupled complex Ginzburg-Landau equation
Gao Jihua†, Shi Wenmao, Zhang Chao, Ge Zaochuan, and Yang Haitao
College of Materials Science and Engineering, Key Laboratory of Special Functional Materials of Shenzhen,Shenzhen University, Shenzhen 518060, Guangdong Province, P.R.China
Abstract:We study the dynamic behavior in a unidirectionally coupled system based on a model of the two-dimensional complex Ginzburg-Landau equation. We discuss the spatiotemporal patterns in the response system driven by a stable amplitude spiral wave with different coupling strengths. By analyzing the synchronization function and frequency characteristic in the amplitudes of the drive system and the response system, we observe the similarity of spiral structures between phase and amplitude under weak coupling conditions. The same phenomenon is also observed with the driving signals of target waves and plane waves, respectively. This proves that the process of synchronization in the unidirectional coupled system has three steps: from out of synchronization to similarity of spiral structures between phase and amplitude, and finally to complete synchronization. This phenomenon explains the occurrence of amplitude spirals.
Key words:differential dynamic system; spatiotemporal system; pattern; complex Ginzburg-Landau equation; coupled system; spiral structures; amplitude spiral
基金项目:深圳市基础研究资助项目(JCYJ 20140418181958489)
作者简介:高继华(1972—),男,深圳大学教授.研究方向:非线性动力学.E-mail: jhgao@szu.edu.cn
中图分类号:O 415.5
文献标志码:A
doi:10.3724/SP.J.1249.2016.03272
【电子与信息科学 / Electronics and Information Science】
Received:2015-12-02;Accepted:2016-03-25
Foundation:Shenzhen Science and Technology Research Foundation(JCYJ 20140418181958489)
† Corresponding author:Professor Gao Jihua. E-mail: jhgao@szu.edu.cn
Citation:Gao Jihua,Shi Wenmao,Zhang Chao,et al. Similarity of spiral structures between phase and amplitude in coupled complex Ginzburg-Landau equation[J]. Journal of Shenzhen University Science and Engineering, 2016, 33(3): 272-280.(in Chinese)
引文:高继华,史文茂,张超,等.耦合复Ginzburg-Landau方程中的相-模螺旋结构相似性[J]. 深圳大学学报理工版,2016,33(3):272-280.

