基于粒子群优化的生物组学数据分类模型选择
杨峻山,纪 震,谢维信,朱泽轩
1) 深圳大学信息工程学院,广东深圳 518060;2) 深圳大学计算机与软件学院,广东深圳 518060
基于粒子群优化的生物组学数据分类模型选择
杨峻山1,纪震1,谢维信1,朱泽轩2
1) 深圳大学信息工程学院,广东深圳 518060;2) 深圳大学计算机与软件学院,广东深圳 518060
摘要:针对生物组学数据普遍存在的高维小样本和样本分布不平衡问题,提出基于粒子群优化分类模型选择算法.该算法中粒子编码由样本平衡模型、特征选择模型和分类模型及超参数构成,粒子种群以达到以生物组学数据最佳分类性能为目标,通过对粒子的速度和位置进行迭代更新,得到模型组合及超参数的最优解.在8组真实生物组学数据集上的实验结果表明,所提模型选择算法能够避免人为选择所带来的主观偏差,提高最佳分类性能和稳定性.
关键词:生物组学;粒子群优化;样本平衡;特征选择;分类模型;模型选择;数据挖掘
生物组学主要是指基因组学、代谢组学、转录组学、免疫组学及脂类组学等的统称[1].通过对组学数据的综合分析,可以更深入地研究疾病的形成机理及其生物过程,找到检测疾病和治疗疾病的相关生物标记物[2].随着生物组学数据规模的日益增长,利用数据挖掘技术解决生物组学中的问题已成为一种必然趋势,其中分类学习是分析生物组学数据常见的手段之一.
生物组学数据通常具有两个特点,即各类样本分布不平衡[3]和高维小样本[4].样本分布不平衡问题容易使分类模型受到多数类样本支配,而忽视少数类样本的信息,影响整体分类的泛化性能.为解决该问题,在分类学习之前对数据采用样本平衡方法进行预处理,可提高分类模型对少数类样本的泛化能力[5].高维小样本容易引起维度灾难从而影响分类模型的学习性能.研究人员经常应用特征选择技术对生物组学数据进行预处理,剔除与分类无关或冗余的特征,有效提高分类学习性能[6].
在数据挖掘领域,已有众多样本平衡模型和特征选择模型.如何针对不同数据和分类器挑选合适的样本平衡模型和特征选择模型的组合,并达到最佳的分类性能仍是一个亟待解决的问题.寻找样本平衡模型、特征选择模型和分类模型的最佳组合以及优化模型的参数(称为超参数)属于复杂优化问题.粒子群优化算法(particle swarm optimization,PSO)实现简单且对复杂优化问题往往可以在合理时间内找到可接受的最优解[7].本研究提出一种基于粒子群优化的模型选择算法(model selection based on PSO,MS-PSO).该算法将候选样本平衡模型、特征选择模型和分类模型以及模型的超参数编码到粒子中,通过种群的不断迭代,自适应搜索具有最优分类性能的模型组合以及超参数设置.
1相关研究述评
样本平衡是一项通过对不平衡样本进行采样或再造使其达到平衡状态的数据预处理技术,主要分为欠采样和过采样两种[8].欠采样是指在多数类样本中抽取与少数类样本数量相当的样本并与少数类样本组成新的平衡数据.随机欠采样(random undersampling,RU)[9]在多数类样本中随机抽取一些样本与少数类样本组成新的平衡数据,其实现机制简单但往往能够取得不错的效果,是最常用于解决生物组学数据样本不平衡问题的方法之一[10].过采样是指通过某种机制对少数类样本进行合成从而增加新的样本,使少数类样本数量增至与多数类样本相当的平衡态.常见的过采样模型包括合成少数类过采样技术(synthetic minority oversampling technique, SMOTE)[11]、borderline-SMOTE[12]和MWMOTE(majority weighted minority oversampling technique)[13].这些方法都已被成功用于解决生物组学数据不平衡问题[11-13].其中最典型的方法是SMOTE,基本思想是在距离较近的少数类样本中增加插值,使少数类样本数量与多数类样本数量达到平衡态.
特征选择作为机器学习或者模式识别前期处理过程,主要负责从完整的特征集合中提取1个最小特征子集使得学习方法性能得到提高或者避免实质性降低.特征选择是一个循环的过程,每1次循环都随机或者根据启发式方法产生候选子集,随后使用独立(不使用学习方法)或者非独立(直接使用学习方法)标准对候选子集进行评估,以上过程不断重复直到满足预先设定的终止条件而产生最佳子集.最佳子集的正确性必须使用独立的测试数据进行验证.根据是否引入学习方法,可以将针对生物组学数据的特征选择技术分为过滤式方法(filter method)、封装式方法(wrapper method)和嵌入式方法(embedded method)[14].过滤式方法在特征子集搜索过程中没有引入学习过程,而是根据数据本身的统计分布特性对特征集合进行评价;而封装式方法在特征子集搜索过程中引入了学习过程,所以过滤式方法速度通常比封装式方法更快;嵌入式方法在训练分类器的同时完成对最优特征子集的搜索,该方法也有较低的计算复杂度.过滤式方法运行高效且具有不错的性能,在解决生物组学数据的特征选择问题上广受青睐.如相关性排序(filter ranking,FR)[15]、最大相关最小冗余法(minimum redundancy maximum relevance,MRMR)特征选择方法[16]和基于相关性的过滤式快速(fast correlation-based filter,FCBF)特征选择方法[17]等对高维生物组学数据的分类性能都有明显的提升.
目前已有几种比较典型的模型选择算法.2002年,Momma等[18]提出一种用于支持向量机和分类模型选择的模式搜索算法.鉴于此类问题属于复杂优化问题,基于进化计算的模型选择算法应运而生.其中最具代表性的是Escalante等[19]提出的基于粒子群优化的模型选择算法(particle swarm model selection,PSMS).该算法使用粒子群优化算法在候选模型的组合中搜索一组具有最佳学习性能的模型组合.实验结果表明,这种基于启发式群智能优化的模型选择算法,在特征数低于60的二分类乳腺癌和甲状腺癌的基因组学数据集上具有较好的预测效果.Rosales-Pérez 等[20]提出多目标模型选择方法(multi-objective model type selection,MOMTS).该方法使用基于分解的多目标进化算法优化模型组合和超参数,将经验误差、训练误差和模型复杂度作为优化目标.选取了5种分类模型作为MOMTS的候选优化模型,并在包括生物组学在内的13组维度低于60的标准测试数据上做了与PSMS的对比试验,结果证明MOMTS具有更好的泛化性能.
PSMS和MOMTS模型选择算法主要针对数据维数低于100维的二分类问题,并没有针对样本分布不平衡的高维(维度在100~20 000)生物组学数据的多分类问题.为针对生物组学数据特有的多类样本分布不平衡和高维小样本的特点并获得具有较好分类效果的模型组合,本研究提出生物组学数据分类模型选择算法MS-PSO.考虑到模型及超参数所构成的搜索空间维度通常较低,本研究采用低维空间中搜索性能不错,且简单易实现的粒子群优化算法作为模型选择的搜索算法,以达到最优的分类性能为优化目标,优化样本平衡模型、特征选择模型和分类模型的组合及超参数设置.
2粒子群优化模型选择
2.1整体框架
MS-PSO整体流程分3步完成.第1步,考虑到生物组学数据通常存在多类标的情况,需要将内部数据二分类化为若干两分类子数据,得到用于训练分类模型的子训练数据和用于计算粒子适应度的子测试数据.第2步,使用PSO优化候选模型组合是一个循环迭代的过程.在每个两分类分支中,子训练数据通常具有样本分布不平衡和高维的特点,为获得合理的适应度,需先将子训练数据通过样本平衡模型和特征选择模型预处理后再用于训练分类模型,然后分类模型对子测试数据完成分类预测,并将预测结果作为粒子适应度.在PSO到达预先设定的最大迭代次数时停止,全局最优粒子代表样本平衡模型、特征选择模型和分类模型的最佳组合以及最优的超参数.第3步,先将外部数据经若干子分类分支的最优特征选择模型预处理,再由最优分类模型完成预测,最后将所有两分类分支的分类结果投票集成.MS-PSO总体框架如图1.MS-PSO伪代码如图2.

图1 MS-PSO总体框架Fig.1 Framework of MS-PSO
2.2样本平衡模型
MS-PSO中所优化的候选样本平衡模型有3种,分别是RU、SMOTE和用于参考的不采用样本平衡模型(no sampling,NS).SMOTE的参数近邻值n作为MS-PSO优化的超参数.
2.3特征选择模型
鉴于过滤式方法运行高效且具备不错的性能表现,本研究选取3种常用于生物组学数据的过滤式特征选择方法FR、MRMR和FCBF作为MS-PSO中候选特征选择模型.采用互相关信息量作为FR和MRMR中的相关性度量.3种特征选择模型所选择的特征数m作为MS-PSO优化的超参数.

图2 MS-PSO伪代码Fig.2 Pseudo-code of MS-PSO
2.4分类模型
MS-PSO中所优化的候选分类模型有3种,分别是基于函数类方法——支持向量机(support vector machine,SVM)分类模型,基于聚类技术的分类方法——K近邻(K-nearestneighbor,KNN)分类模型和基于决策树的方法——随机森林(random forest,RF)分类模型.MS-PSO对SVM优化的超参数有复杂度参数c、 样本预处理方法p(3种方式)和内核类型e(4种内核),如表1.MS-PSO对KNN和RF优化的超参数分别是近邻个数k和所建立树的个数t.
2.5粒子编码规则
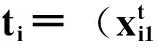
2.6适应度函数
在MS-PSO进化过程中需要对粒子适应度函数合理评估.鉴于生物组学数据通常具有高维小样本的特点,外部验证方案能够针对小样本数据提供更准确的评估结果[21].所以将整体数据分成外部数据和内部数据,适应度评估过程采用内部交叉验证,即将候选分类模型对内部数据的交叉验证分类准确率作为MS-PSO的粒子适应度.

表1 粒子位置xij编码规则
2.7粒子速度和位置更新规则
第t代的惯性因子为
ω=Ωmax-t(Ωmax-Ωmax)/I
(1)
其中,Ωmax和Ωmin是预设上下界; I为预先设置的最大迭代次数.
(2)
其对应的粒子速度为
(3)
其中, c1和c2是加速因子; r1和r2是均匀分布在[0,1]中的随机数.
2.8计算复杂度
设样本平衡模型的计算复杂度为α, 特征选择模型的计算复杂度为β, 分类模型的计算复杂度为γ, 适应度函数评估采用L折交叉验证,最大迭代次数为I, 粒子个数N, 数据类别数为C(C≥3), 则MS-PSO的计算复杂度为
ρ=N(I+1)(α+β+γ)LC
(4)
其中, α取决于数据样本个数; β和γ取决于数据特征个数.
3实验结果分析
为评估MS-PSO在生物组学数据分类问题上的有效性,在如表2的8组真实生物组学数据上进行分类性能比较测试.这些数据集大都具有较严重的样本不平衡现象.将表1中3种分类模型(KNN、SVM和RF)、3种样本平衡模型(NS、RU和SMOTE)以及3种特征选择模型(FR、FCBF和MRMR)的所有可能的组合称为固定模型选择(fixed model selection,FMS),共3×3×3=27种.实验将MS-PSO和FMS在分类准确率上进行测试并比较优劣.每个FMS超参数由经验设定,如表3.
本研究使用试差法获得PSO最优参数和超参数范围设置,即粒子个数N=20、 I=20、 c1=c2=2、 Ωmax=1、 Ωmin=0. MS-PSO和FMS的性能评估采用外部三折交叉验证,即内部数据用于评估粒子适应度,外部数据用于评估分类性能.首先,评估MS-PSO分类性能.先在整体数据中随机抽取2/3的样本作为计算粒子适应度的内部训练数据,剩下的1/3样本用于MS-PSO分类性能评估.然后,令FMS中的特征选择模型的特征个数与MS-PSO所选择特征的个数保持一致的条件下,完成27种FMS分类性能测试.为减少实验偏差,本研究统计了10次实验分类准确率的平均值,结果如图3.图3中序号坐标28对应MS-PSO,序号坐标1~27对应27种FMS.假设FMS的序号坐标为u, 由式(5)和式(6)可得FMS中所选择的特征选择模型和样本平衡模型.
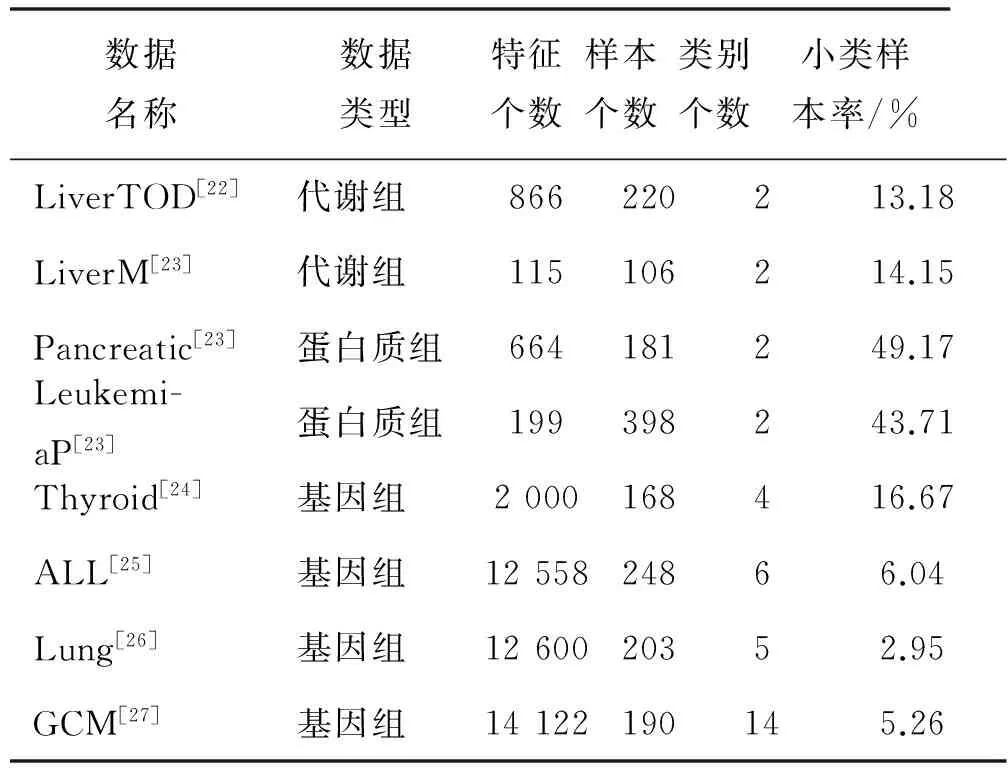
表2 实验所用生物组学数据集
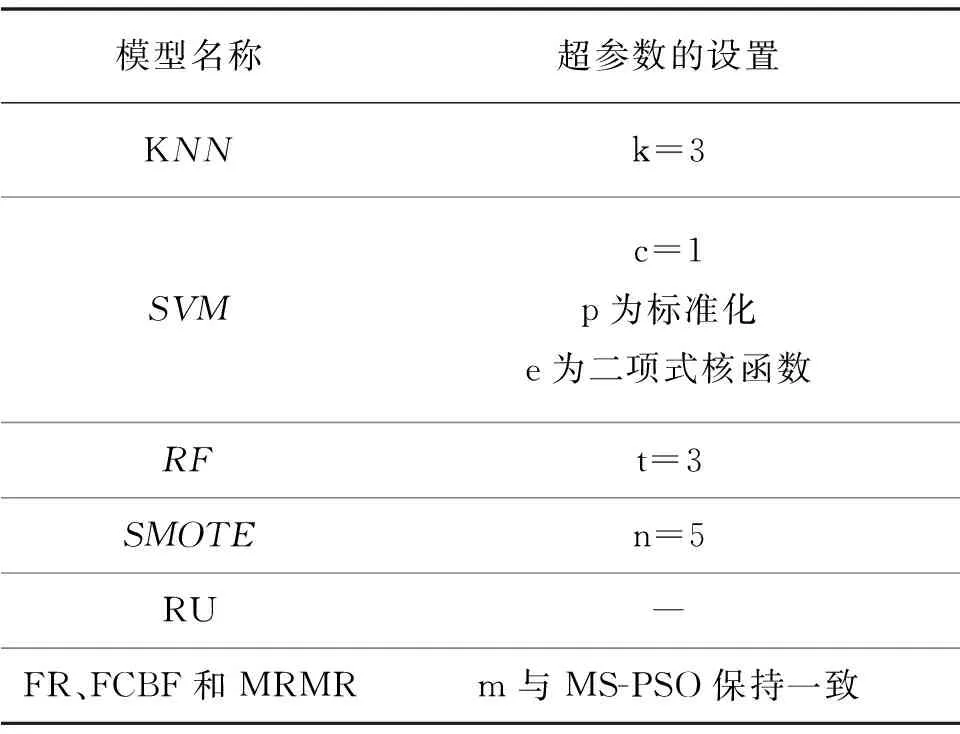
表3 固定模型选择的超参数设置

(5)
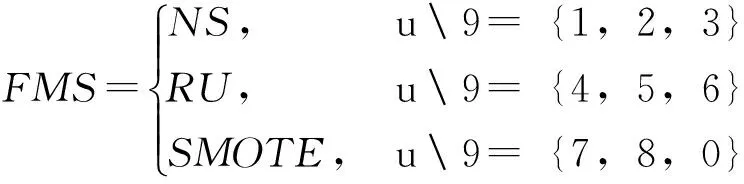
(6)
其中,符号表示求余运算.

图3 FMS和MS-PSO实验结果比较Fig.3 Comparison of simulation results of FMS and MS-PSO
由图3可见,从分类模型角度分析,不同分类模型在不同数据上具有明显的分类性能差异,如KNN在LiverTOD、ALL、Lung和GCM上表现优于SVM和RF,而在其他数据上的表现并不佳.SVM对LiverM和LeukemiaP的分类性能较突出.从样本平衡模型角度分析,数据集LiverTOD、LiverM、Thyroid、ALL、Lung和GCM的样本分布不平衡现象严重,将它们经SMOTE过采样预处理后对分类性能的提升比US和NS更明显,而Pancreatic和LeukemiaP数据集样本分布较为平衡,不对其进行样本平衡预处理反而更有利于分类预测.其原因是类别个数越多,在MS-PSO每个子分类分支中内部子训练数据的样本分布越不平衡,采用SMOTE将样本由不平衡状态转变为平衡状态,会提高小类样本的数量,有益于获得较好的分类预测性能.从特征选择模型角度分析,RF和MRMR通常比FCBF更有助于提高分类性能.由以上分析可知,不存在固定的模型组合能在所有数据上都保持最好的分类性能.表4给出最优的FMS和MS-PSO分类准确率的定量对比.由表4和图3可见,MS-PSO在每个数据上都能达到或接近最突出的分类预测性能.

表4 MS-PSO与最优FMS分类准确率对比
图4给出MS-PSO的最优模型组合中每个模型在10次实验中被选择次数的统计结果.由图4可见,在每组数据中,基本上都存在占支配地位的模型,即该模型被选中的次数明显高于其他模型.这说明MS-PSO能够针对不同生物组学数据样本分布和特征的特点,自适应且稳定地选择到具有最佳分类性能的样本平衡模型、特征选择模型和分类模型的组合,同时获得这组模型的超参数.

图4 MS-PSO的模型被选择次数统计Fig.4 Statistics of selected frequencies for models in MS-PSO
结语
提出基于粒子群优化算法的生物组学数据分类模型选择算法MS-PSO,并结合真实生物组学数据对MS-PSO和FMS的分类性能进行了系统比较和研究.实验结果表明,MS-PSO能够根据不同生物组学数据的样本分布和特征,自适应选择样本平衡模型和特征选择模型的组合,使这一模型组合在某一分类模型上达到较好的分类性能,避免了人为选择所导致的主观偏差.在后续工作中,将会考察更多的启发式搜索算法在模型选择中的表现.完善算法并提供相应软件,使其能够被更多生物信息学领域的研究人员所应用.
参考文献/References:
[1] Marchionni L, Geman D. Predicting cancer phenotypes with mechanism-driven multi-omics data integration[J]. Cancer Research, 2015, 75(15): 261-274.
[2] Swan A L, Stekel D J, Hodgman C, et al. A machine learning heuristic to identify biologically relevant and minimal biomarker panels from omics data[J]. BMC Genomics, 2015, 16(s1): S2.
[3] Triguero I, Rio S, Lopez V, et al. ROSEFW-RF: The winner algorithm for the ECBDL’14 big data competition: an extremely imbalanced big data bioinformatics problem[J]. Knowledge-Based Systems, 2015, 87: 69-79.
[4] Yao F, Coquery J, Lê Cao K A. Independent principal component analysis for biologically meaningful dimension reduction of large biological data sets[J]. BMC Bioinformatics, 2012, 13(1): 24.
[5] Ambroise C, McLachlan G. Selection bias in gene extraction on the basis of microarray gene-expression data[J]. Proceedings of the National Academy of Sciences of the United States of America, 2002, 99(10):6562-6566.
[6] Christin C, Hoefsloot H C J, Smilde A K, et al. A critical assessment of feature selection methods for biomarker discovery in clinical proteomics[J]. Molecular & Cellular Proteomics, 2013, 12(1): 263-276.
[7] 薛丽萍,尹俊勋,纪震.基于粒子群优化-模糊聚类的说话人识别[J].深圳大学学报理工版,2008,25(2):178-183.
Xue Liping, Yin Junxun, Ji Zhen. Speaker recognition based on particle swarm optimization and fuzzy clustering analysis[J]. Journal of Shenzhen University Science and Engineering, 2008, 25(2): 178-183.(in Chinese)
[8] 曾磐,朱安民.基于支持向量机的NBA季后赛预测方法[J].深圳大学学报理工版,2016,33(1):62-71.
Zeng Pan, Zhu Anmin. A SVM-based model for NBA playoffs prediction[J]. Journal of Shenzhen University Science and Engineering, 2016, 33(1): 62-71.(in Chinese)
[9] Weiss G M, Provost F. The effect of class distribution on classifier learning: an empirical study: University Technical Report ML-TR-44[R]. Piscataway, USA: Rutgers, 2001.
[10] Khoshgoftaar T M, Fazelpour A, Dittman D J, et al. Classification performance of three approaches for combining data sampling and gene selection on bioinformatics data[C]// IEEE 15th International Conference on Information Reuse and Integration. Redwood City, USA: IEEE, 2014: 315-321.
[11] Chawla N V, Bowyer K W, Hall L O, et al. SMOTE: synthetic minority over-sampling technique[J]. Journal of Artificial Intelligence Research, 2002, 16(1): 321-357.
[12] Han Hui, Wang Wenyuan, Mao Binghuan. Borderline-SMOTE: a new over-sampling method in imbalanced data sets learning[C]// International Conference on Intelligent Computing. Berlin: Springer Berlin Heidelberg, 2005: 878-887.
[13] Barua S, Islam M M, Yao X, et al. MWMOTE-majority weighted minority oversampling technique for imbalanced data set learning[J]. IEEE Transactions on Knowledge and Data Engineering, 2014, 26(2): 405-425.
[14] Saeys Y, Inza I, Larraaga P. A review of feature selection techniques in bioinformatics[J]. Bioinformatics, 2007, 23(19): 2507-2517.
[15] Lazar C, Taminau J, Meganck S, et al. A survey on filter techniques for feature selection in gene expression microarray analysis[J]. IEEE Transactions on Computational Biology and Bioinformatics, 2012, 9(4): 1106-1119.
[16] Ding C, Peng Hanchuan. Minimum redundancy feature selection from microarray gene expression data[J]. Journal of Bioinformatics and Computational Biology, 2005, 3(2): 185-205.
[17] Yu Lei, Liu Huan. Feature selection for high-dimensional data: a fast correlation-based filter solution[C]// Proceedings of the 20th International Conference on Machine Leaning. Washington D C, USA:[s. n.], 2003, 2: 856-863.
[18] Momma M, Bennett K P. A pattern search method for model selection of support vector regression[C]// Proceedings of the 2nd SIAM International Conference on Data Mining. Arlington, USA:[s. n.], 2002: 261-274.
[19] Escalante H J, Montes M, Sucar L E. Particle swarm model selection[J]. The Journal of Machine Learning Research, 2009, 10: 405-440.
[20] Rosales-Pérez A, Gonzalez J A, Coello C A C, et al. Multi-objective model type selection[J]. Neurocomputing, 2014, 146: 83-94.
[21] Ambroise C, McLachlan G J. Selection bias in gene extraction on the basis of microarray gene-expression data[J]. Proceedings of the National Academy of Sciences of the United States of America, 2002, 99(10): 6562-6566.
[22] Zhou Jiarui, Zhu Zexuan, Ji Zhen. A memetic algorithm based feature weighting for metabolomics data classification[J]. Acta Electronica Sinica, 2014, 23(4): 706-711.
[23] He Shan, Chen Huanhuan, Zhu Zexuan, et al. Robust twin boosting for feature selection from high-dimensional omics data with label noise[J]. Information Sciences, 2015, 291: 1-18.
[24] Yukinawa N, Oba S, Kato K, et al. A multi-class predictor based on a probabilistic model: application to gene expression profiling-based diagnosis of thyroid tumors[J]. BMC Genomics. 2006, 7(1):190.
[25] Yeoh E J, Ross M E, Shurtleff S A, et al. Classification, subtype discovery, and prediction of outcome in pediatric acute lymphoblastic leukemia by gene expression profiling[J]. Cancer Cell, 2002, 1(2): 133-143.
[26] Bhattacharjee A, Richards W G, Staunton J, et al. Classification of human lung carcinomas by mRNA expression profiling reveals distinct adenocarcinoma subclasses[J]. Proceedings of the National Academy of Sciences of the United States of America, 2001, 98(24):13790-13795.
[27] Ramaswamy S, Tamayo P, Rifkin R, et al. Multiclass cancer diagnosis using tumor gene expression signatures[J]. Proceedings of the National Academy of Sciences of the United States of America, 2001, 98(26): 15149-15154.
【中文责编:英子;英文责编:子兰】
Model selection based on particle swarm optimization for omics data classification
Yang Junshan1, Ji Zhen1†, Xie Weixin1, and Zhu Zexuan2
1) College of Information Engineering, Shenzhen University, Shenzhen 518060, Guangdong Province, P.R.China 2) College of Computer Science and Software Engineering, Shenzhen University, Shenzhen 518060,Guangdong Province, P.R.China
Abstract:A new model selection algorithm based on particle swarm optimization is proposed for omics data classification. Specifically, the algorithm is designed to handle the high dimensionality, small sample size and class imbalance problems that are inherent in omics data. The particles encode candidate combinations of data sampling, feature selection, classification models and their corresponding parameter settings. The swarm optimization is targeted at the best classification performance. The particle velocity and position are iteratively updated until some stopping criteria are met and then the optimal solution model combination is output. The simulation results on eight real-world omics datasets show that the proposed model selection algorithm is capable of avoiding the bias introduced by manual settings and leading to accurate and reliable classification performance.
Key words:omics dataset; particle swarm optimization; data sampling; feature selection; classification model; model selection; data mining
基金项目:国家自然科学基金资助项目(61171125, 61471246)
作者简介:杨峻山(1981—),男,深圳大学博士研究生.研究方向:信号与信息处理.E-mail:junshan763@126.com
中图分类号:TP 181
文献标志码:A
doi:10.3724/SP.J.1249.2016.03264
【电子与信息科学/Electronics and Information Science】
Received:2016-02-26;Accepted:2016-04-10
Foundation:National Natural Science Foundation of China (61171125, 61471246)
† Corresponding author:Professor Ji Zhen.E-mail:jizhen@szu.edu.cn
Citation:Yang Junshan, Ji Zhen, Xie Weixin, et al. Model selection based on particle swarm optimization for omics data classification[J]. Journal of Shenzhen University Science and Engineering, 2016, 33(3): 264-271.(in Chinese)
引文:杨峻山,纪震,谢维信,等.基于粒子群优化的生物组学数据分类模型选择[J]. 深圳大学学报理工版,2016,33(3):264-271.

