矩阵方程AX=B, XC=D的(M,N)-反对称解

刘　巍， 王柏育

(长沙学院 数学与计算机科学系， 湖南 长沙　410022)



矩阵方程AX=B, XC=D的(M,N)-反对称解

刘巍， 王柏育*

(长沙学院 数学与计算机科学系， 湖南 长沙410022)

摘要：利用奇异值分解和广义奇异值分解，得到了矩阵方程AX=B,XC=D的(M,N)-反对称解存在的充要条件，给出了通解表达式及其最佳逼近问题的解，并提供了数值例子来说明理论结果的正确性.

关键词：(M,N)-反对称矩阵； 最佳逼近； 广义奇异值分解

0引言

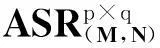
定义1[1]对矩阵A=(aij)∈Rn×m和B=(bij)∈Rn×m，称A*B=(aijbij)∈Rn×m是A与B的Hadamard乘积.

定义2给定M∈Rn×p，N∈Rq×n，如果(MXN)T=-MXN，称X是(M,N)-反对称矩阵.

近些年来，文献[2-16]讨论了矩阵方程的无约束解、(反)对称解、广义(反)对称解、广义自反解、(R,S)-对称解、(R,S)-共轭解、Hermitian自反解和最小二乘解等，并得到了很好的结果.

本文研究以下问题：

AX=B,XC=D

(1)

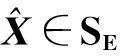
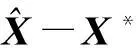
(2)

其中,SE是问题I的解集合.

1问题Ⅰ的解

在本节中，利用矩阵的SVD分解和GSVD分解[2]，给出问题I有解的充要条件以及一般解的表达式.

(3)

其中:

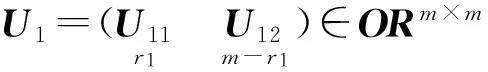
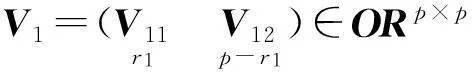
Σ1=diag(σ11,…,σ1r1)>0，

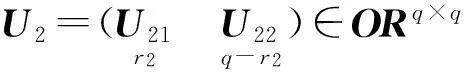
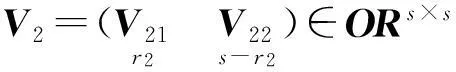
Σ2=diag(σ21,…,σ2r2)>0.

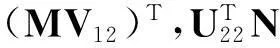
(4)

其中:

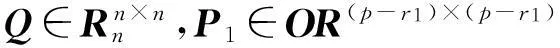
P2∈OR(q-r2)×(q-r2),

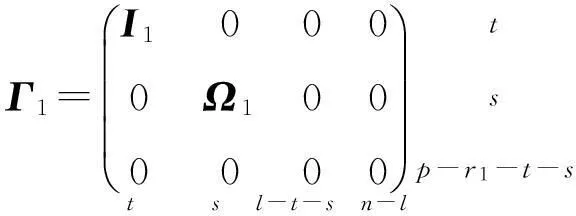
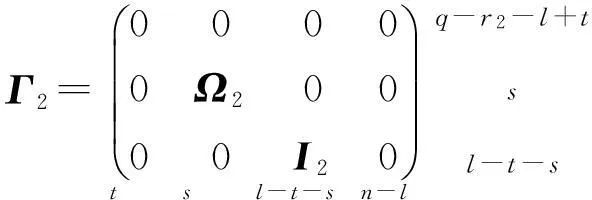
(5)

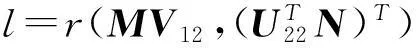
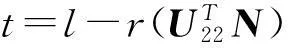
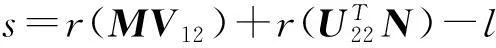
Ω1=diag(α1,…,αs)>0,

Ω2=diag(β1,…,βs)>0,

1>α1≥…≥αs>0,

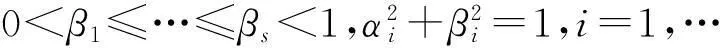
引理3若矩阵F∈Rn×n,G0∈SRn×n满足

G0=F+FT, 则:

其中,G∈ASRn×n.

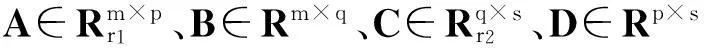
AA+B=B,DC+C=D,BC=AD

(6)

并且其一般解的表达式为:

(7)

其中,X22是任意的(p-r1)×(q-r2)阶实矩阵，V12、U22如引理1中所定义.

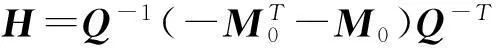
M0=M(A+B+(I-A+A)DC+)N,

矩阵H的分块如下

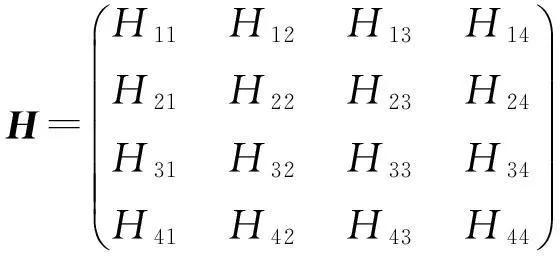
其中,Q如引理2中所定义，Hii(i=1,2,3,4)是对称矩阵.则问题Ⅰ的解集SE非空的充要条件是:

(ⅰ)AA+B=B,DC+C=D,BC=AD.

(ⅱ)H11=0,H33=0,Hi4=0,H4i=0,

1≤i≤4.

当问题Ⅰ有解时，其一般解的表达式为:

X=A+B+(I-A+A)DC++

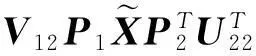
(8)

其中:

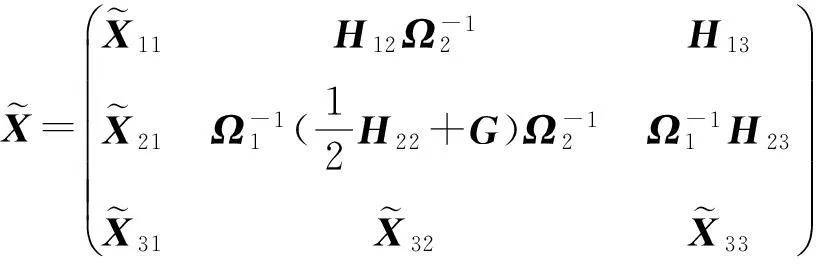
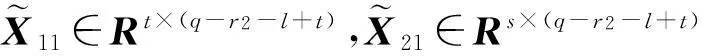
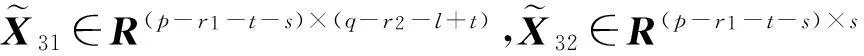
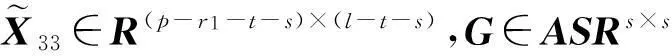
V12、U22、P1、P2、Ω1、Ω2如引理1和引理2中所定义.

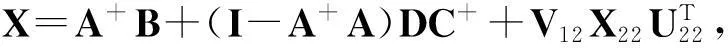
由(MXN)T=-MXN，有:

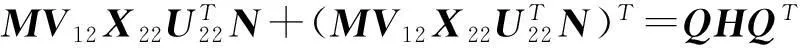
由引理2可得:

(9)

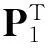
(10)

将式(5)和式(10)代入式(9)，得:

所以:

H11=0,H33=0,Hi4=0,H4i=0,1≤i≤4

(11)

(12)

(13)

式(11)即条件(ⅱ).

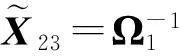
2问题Ⅱ的解

注意到问题Ⅰ的解集是一个闭凸集.因此,问题Ⅱ存在唯一解.先给出以下引理.

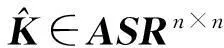
(14)

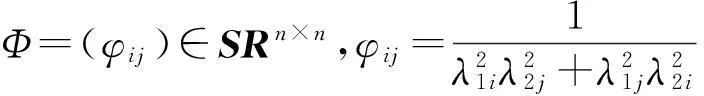
证明:设K=(kij)∈ASRn×n,L=(lij)∈Rn×n,则:

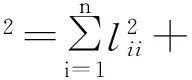
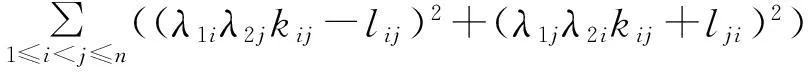
且F(K)是连续可微函数，根据函数在某点处取极小值的必要条件，可得:

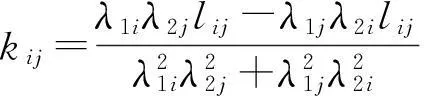
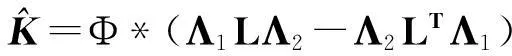
定理2给定矩阵X*∈Rp×q、M∈Rn×p、

D∈Rp×s,令

的分块如下:

(15)

(16)

其中:

(17)

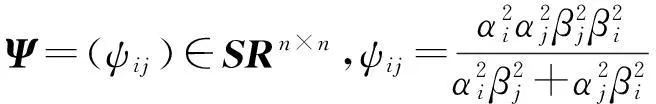
V12、U22、P1、P2、Ω1、Ω2如引理1和引理2中所定义.

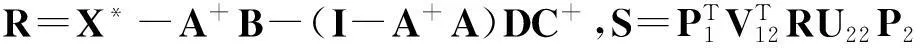
‖X-X*‖2=

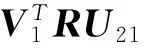
min

(18)

对S作形如式(15)的分块，则式(18)等价于

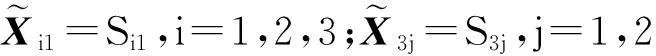
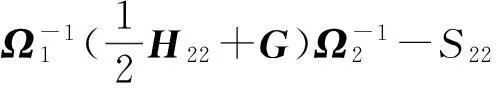
(19)

3数值例子

在本节中，给出相应的数值例子，说明所得理论结果的正确性.

例1考虑矩阵方程AX=B,XC=D,其中

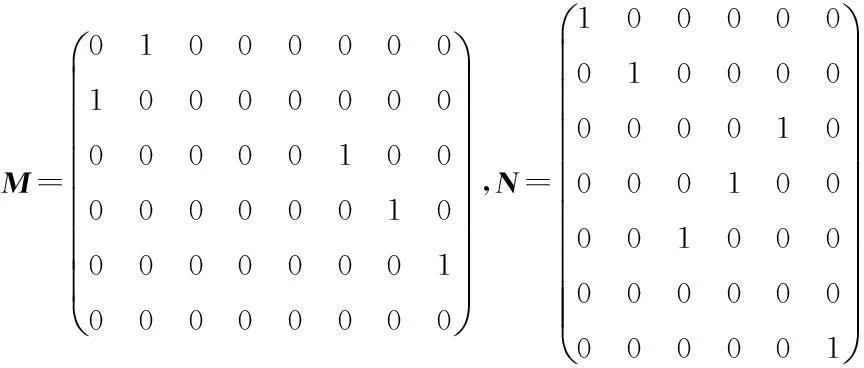
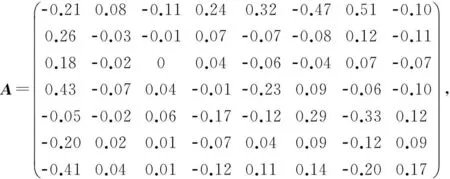
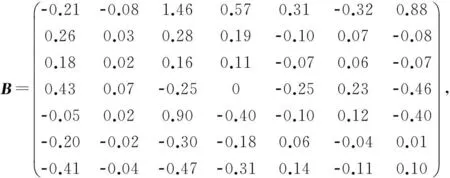
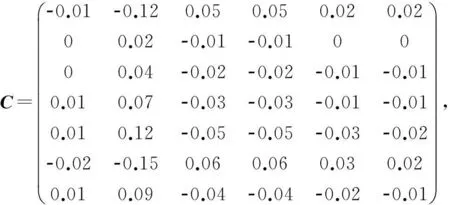
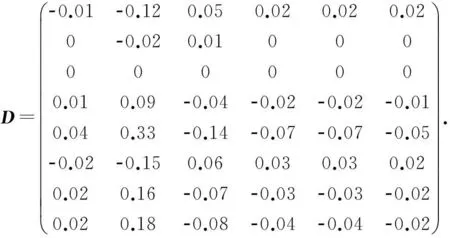
经验证，满足定理1的条件，在式(8)中，取可任意取值的矩阵均为零矩阵，可得问题I的一个解为:

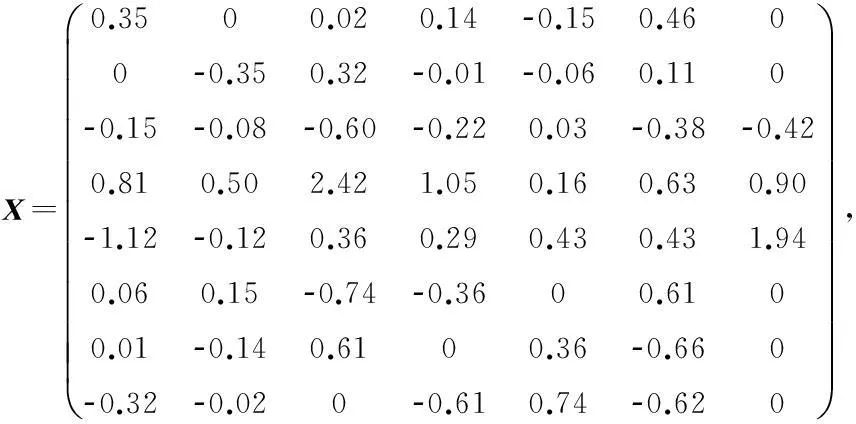
且有:

‖AX-B‖=9×10-16,‖XC-D‖=6×10-17,

‖(MXN)T+MXN‖=5×10-15

给定

根据式(16)，可得问题Ⅱ的解为：

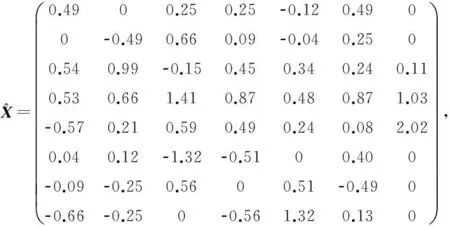
且有：

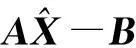
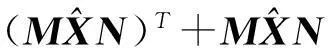
参考文献

[1]R.A.Horn,C.R.Johnson.矩阵分析(英文版)[M].北京:人民邮电出版社,2005.

[2]K.W.E.Chu.Singularvalueandgeneralizedsingularvaluedecompositionandthesolutionoflinearmatrixequations[J].LinearAlgebraAppl.,1987,88-89:83-98.

[3]S.K.Mitra.ApairofsimultaneouslinearmatrixequationsA1XB1=C1,A2XB2=C2andamatrixprogrammingproblem[J].LinearAlgebraAppl.,1990,131:107-123.

[4]S.K.Mitra.ThematrixequationsAX=C,XB=D[J].LinearAlgebraAppl.,1984,59:171-181.

[5]A.Navarra,P.L.Odell,D.M.Yong.ArepresentationofthegeneralcommonsolutiontothematrixequationsA1XB1=C1,A2XB2withapplications[J].ComputersandMathematicswithApplications,2001,41(7-8):929-935.

[6]W.F.Trench.Inverseeigenproblemsandassociatedapproximationproblemsformatriceswithgeneralizedsymmetryorskewsymmetry[J].LinearAlgebraAppl.,2004,380:199-211.

[7]X.Y.Peng,X.Y.Hu,L.Zhang.AniterativemethodforsymmetricsolutionsandoptimalapproximationsolutionofthesystemofmatrixequationsA1XB1=C1,A2XB2=C2[J].AppliedMathematicsandComputation,2006,183(2):1 127-1 137.

[8]F.L.Li,X.Y.Hu,L.Zhang.Thegeneralizedreflexivesolutionforaclassofmatrixequations(AX=B,XC=D)[J].ActaMathematicaScientia,2008,28B(1):185-193.

[9]S.F.Yuan,A.P.Liao,Y.Lei,LeastsquaresHermitiansolutionofthematrixequation(AXB,CXD)=(E,F)withtheleastnormovertheskewfieldofquaternions[J].Math.Comput.Modelling,2008,48(1-2):91-100.

[10]Y.Y.Qiu,A.D.Wang.LeastsquaressolutionstotheequationsAX=B,XC=Dwithsomeconstraints[J].AppliedMathematicsandComputation,2008,204(2):872-880.

[11]Y.T.Li,W.J.Wu.Symmetricandskew-antisymmetricsolutionstosystemsofrealquaternionmatrixequations[J].ComputersandMathematicswithApplications,2008,55(6):1 142-1 147.

[12]M.Dehghan,M.Hajarian.Matrixequationsover(R,S)-symmetricand(R,S)-skewsymmetricmatrices[J].ComputersandMathematicswithApplications,2010,59:3 583-3 594.

[13]H.X.Chang,Q.W.Wang,G.J.Song.(R,S)-conjugatesolutiontoapairoflinearmatrixequations[J].AppliedMathematicsandComputation,2010,217(1):73-82.

[14]Y.X.Yuan.Least-squaressolutionstothematrixequationsAX=BandXC=D[J].AppliedMathematicsandComputation,2010,216(10):3 120-3 125.

[15]F.X.Zhang,Y.Li,J.L.Zhao.CommonHermitianleastsquaressolutionsofmatrixequationsA1XA1*=B1andA2XA2*=B2subjecttoinequalityrestrictions[J].ComputersandMathematicswithApplications,2011,62(6):2 424-2 433.

[16]S.Zhou,S.T.Yang.TheHermitianreflexivesolutionsandtheanti-Hermitianreflexivesolutionsforaclassofmatrixequations(AX=B,XC=D)[J].EnergyProcedia,2012,17:1 591-1 597.

【责任编辑：晏如松】

The (M,N)-antisymmetric solutions of the matrix equations AX=B,XC=D

LIU Wei， WANG Bai-yu*

(Department of Mathematics and Computer Science, Changsha University, Changsha 410022, China)

Abstract:In this paper,based on the singular value decomposition (SVD) of a matrix and the generalized singular value decomposition (GSVD) of a matrix pair,we establish the solvability conditions of matrix equations AX=B,XC=D for (M,N)-antisymmetric matrices,give the expressions of general solutions and the solution of corresponding optimal approximation problem,and give a numerical example to verify the correctness of the theoretical results.

Key words:(M,N)-antisymmetric matrix; optimal approximation; generalized singular value decomposition

中图分类号：O241.6

文献标志码：A

文章编号：1000-5811(2016)03-0175-05

作者简介:刘巍(1982-)，男，辽宁建平人，讲师，硕士，研究方向：数值代数通讯作者:王柏育(1981-)，女，辽宁建平人，讲师，博士，研究方向：数值代数、偏微分方程，wangbaiyumath@163.com

基金项目：湖南省教育厅科研计划项目(15C0120)

收稿日期:2016-01-13