基于小波分析的雾霾天气分析与预测

杨文光， 林连海， 田立勤

(1.华北科技学院 基础部， 河北 三河　065201; 2.华北科技学院 计算机学院, 河北 三河　065201)



基于小波分析的雾霾天气分析与预测

杨文光1， 林连海1， 田立勤2

(1.华北科技学院 基础部， 河北 三河065201; 2.华北科技学院 计算机学院, 河北 三河065201)

摘要：随着社会的发展，雾霾天气已经成为中国一种常见的环境灾害.本文选择雾霾天气产生源头之一的工业废气的处理作为主要研究对象，将我国2000～2013年的二氧化硫排放量、烟尘排放量以及每年在工业治理废气上的投放资金作为预测指标，运用小波分析方法，将二氧化硫排放量以及烟尘排放量数据分解到两个不同的高低频道上，根据其周期性建立预测模型，从工业废气的排放角度来预测我国未来的雾霾发展趋势；对我国每年在工业治理废气上的投放资金建立了线性模型，以用于我国未来雾霾天气投资情况的决策分析.预测结果表明，我国近年在废气治理方面的投资略显不足，未来我国的二氧化硫污染会减轻，但是烟尘污染却会稍稍加重.因此，有必要增大对废气治理的投资.

关键词：雾霾； 小波分析； 工业废气； 预测

0引言

在中国经济社会不断发展、城市化进程日渐加快的当今，雾霾天气逐渐被人们所熟知.雾霾造成了城市大面积低能见度的天气现象，这种现象又分成雾和霾两种.雾霾天气对城市发展和人体健康具有较大影响，如影响人的身体健康以至于心理健康，形成酸雨以及导致农业减产等[1].

雾霾的成因复杂，主要是由大气相对湿度、风速、气温等气象要素和PM2.5/PM10浓度等环境要素共同作用而形成[2,3].此外，雾霾污染情况还受到政府政策的影响.因此,对于雾霾的预测存在很多不确定因素，直接对其预测的难度较大.

近年来，已有不少学者运用非线性的预测方式对雾霾天气进行了预测，其中,运用神经网络方法进行预测的模型较多[4-10]，考虑的雾霾影响指标比较单一.艾洪福和石莹等[5]运用BP神经网络，设计了连接权和阈值的修正方法，对长春市的PM2.5进行预测，建立了基于时间序列的BP神经网络雾霾天气预测模型；白鹤鸣等[6]对北京市的API指数分春、夏、秋、冬四季分别建立BP神经网络模型，借此消除雾霾预测的季节性.

侯琼煌和杨航等[11]对二氧化硫排放量、烟尘排放量以及环境污染总治理投资三者建立了时间序列预测模型，运用三次指数平滑法加以预测，实现了对我国雾霾情况的趋势预测;王海鹏等[12]运用一维连续Morlet小波变换研究了兰州市大气污染时间多尺度变化特征、主周期和影响因素，得到了较全面的分析结果.为进一步提高预测精度，本文选择了小波分析方法，运用小波多维度分解的能力建立了非线性模型，将雾霾研究中的影响因素进行缩减，将工业废气排放量作为研究指标.

本文以二氧化硫排放量、烟尘排放量以及我国每年在工业治理废气上的投放资金作为预测指标，使用离散小波分析将二氧化硫排放量、烟尘排放量分别分解到高频和低频两个频道.对低频上的数据建立线性模型和周期曲线模型，其中，线性模型用于预测总体发展趋势，而周期曲线模型则用于模拟雾霾预测的不确定性；将高频上的数据视作噪音数据，只建立周期函数模型进行拟合预测；然后，进行离散小波逆变换得到最终预测值.将我国每年在工业治理废气上的投放资金用最小二乘法做线性拟合，用以分析我国废气治理的投资情况；最后，结合我国雾霾天气主要参数指标进行实例分析，表明本文所提方法的可行性与有效性.

1小波分析

小波分析或称小波变换，是指用有限长或快速衰减的母小波的振荡波形来表示信号.小波变换分为离散小波变换和连续小波变换两种类型.最早产生的小波变换是哈尔小波，由Haar在1910年提出，但那时候小波的概念还没有产生.自1981年之后，小波分析就进入了快速发展阶段，同时小波分析也在多个领域发挥作用[13].通过小波分析，分解后信号的平稳性比原先的信号要好，对某些非平稳的时间序列分解后，便可以采用平稳时间序列进行预测[14].

常用的离散小波分析(Discrete Wavelet Transform,DWT)，是对基本小波的尺度和平移进行离散化，其实现过程可描述为[15]：

z(t)的连续小波变换，即将L2(R)空间中的函数z(t)在小波基下展开，表达如下：

WTz(a,b)=

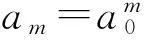
φm,n(t)=2-m/2φ(2-mt-n)

则关于任意函数z(t)的离散小波变换为：

WTz(m,n)=

=2-m/2∫Rz(t)φ(2-mt-n)dt

在MATLAB编程中，离散小波分析可以用MATLAB的dwt函数来实现，逆变换可以用i-dwt函数来实现.

2基于小波分析的雾霾天气预测模型

将二氧化硫排放量和烟尘排放量作为输入，运用离散小波分析，将其分解成低频系数向量cA(t)和高频系数向量cD(t)，将cA(t)作为二氧化硫排放量与烟尘排放量各自预测的主要组成部分;将cD(t)作为预测的噪音部分，分别对这两者建立模型进行预测，然后,通过离散小波分析的逆变换获得预测值,即预测值F的表达式如下：

F(t)=idwt(cA(t),cD(t))

(1)

其中，idwt表示离散小波分析的逆变换.

对于能够表示预测数据主体部分的低频系数向量cA(t)，将其分解成两部分:一部分是线性递增或递减的部分，具体操作方式是求它的线性回归方程;另一部分是随着时间变化而呈现周期变化的部分.为了操作简便，首先求出回归方程，然后从cA(t)中减去回归方程的预测值，用得到的数据做周期曲线拟合，再通过逆运算预测cA(t)：

L(t)=aLt+bL

(2)

T(t)=cA(t)-L(t)

(3)

其中，L(t)是cA(t)向量的回归曲线方程;T(t)是从cA(t)中减去回归方程的预测值.

在对T(t)函数进行曲线拟合时，本文采用由MATLAB软件提供的Fourier曲线拟合功能，并且采取下述预测形式：

T(t)=a0+a1cos(wt)+b1sin(wt)+

a2cos(2wt)+b2sin(2wt)

(4)

对于高频系数向量cD(t)，视作噪音数据，直接运用式(4)作为预测方程进行预测.整个雾霾天气预测模型的预测步骤如图1所示.

图1　预测步骤

3雾霾天气预测

以中华人民共和国国家统计局编写的《中国统计年鉴2014》上的数据作为数据源[16]，侯琼煌和杨航[11]依据上述数据进行雾霾天气主要指标预测的相对误差较大.在此，为了比较本文与参考文献[11]的预测效果差异，选用《中国统计年鉴2014》[16]给出的2002～2012年共计11组数据中的SO2排放量与烟尘排放量作为输入，并将2013年的SO2排放量与烟尘排放量作为验证数据，以检验预测精度.同时，为了更好地进行废气治理决策，选择了工业废气治理投放资金作为第三个指标，以表征环境污染治理投资总额.原始数据如表1所示.

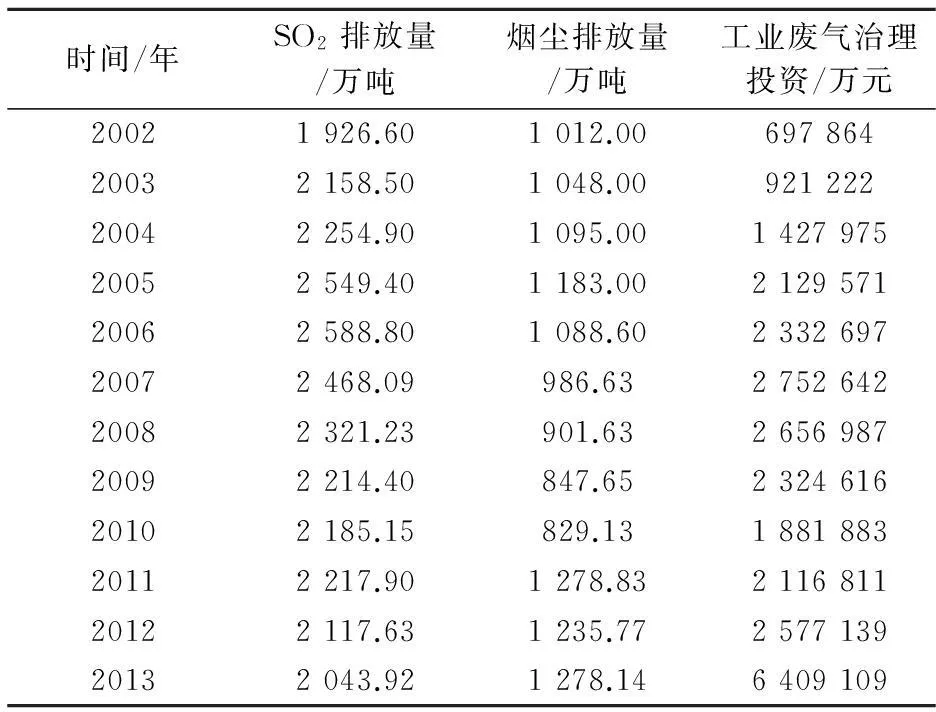
表1　2002～2013年各指标数值[16]

选取2002～2012年的数据，运用MATLAB的离散小波分析函数，将二氧化硫排放量和烟尘排放量分解到低频和高频，其分解情况见表2(精确到小数点后一位)所示，图2、图3是二氧化硫排放量和烟尘排放量分解后折线图.图2、图3中的重构值与真实值两条曲线几乎完全重合.

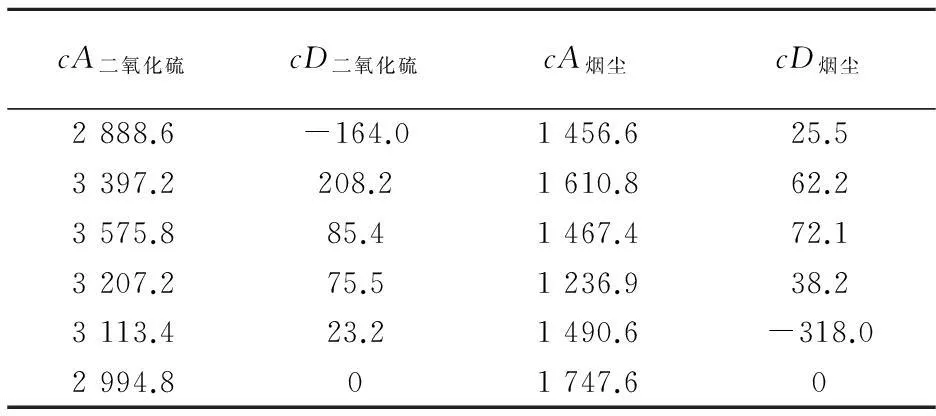
表2　二氧化硫和烟尘排放量的分解系数

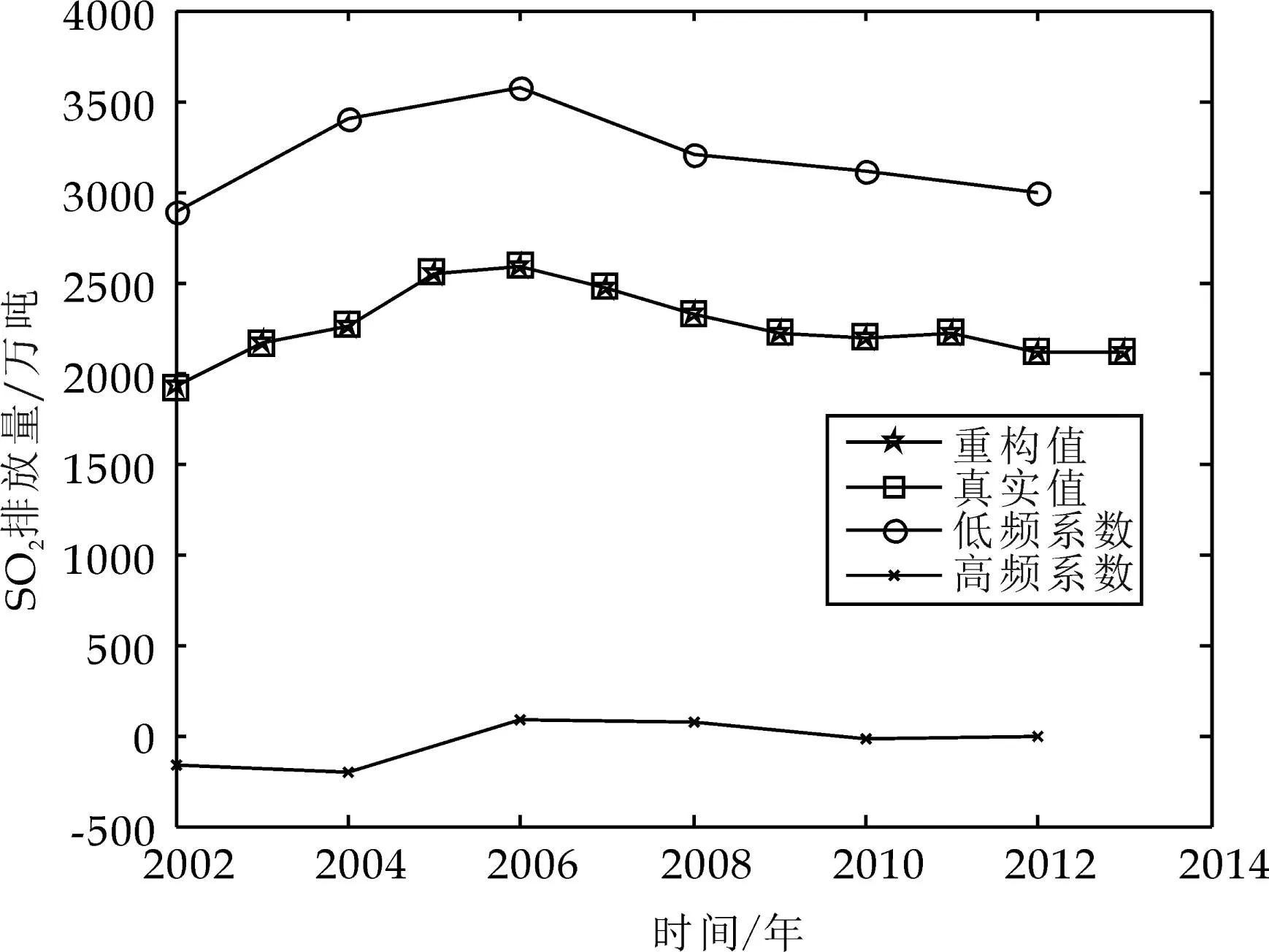
图2　二氧化硫排放量分解折线图

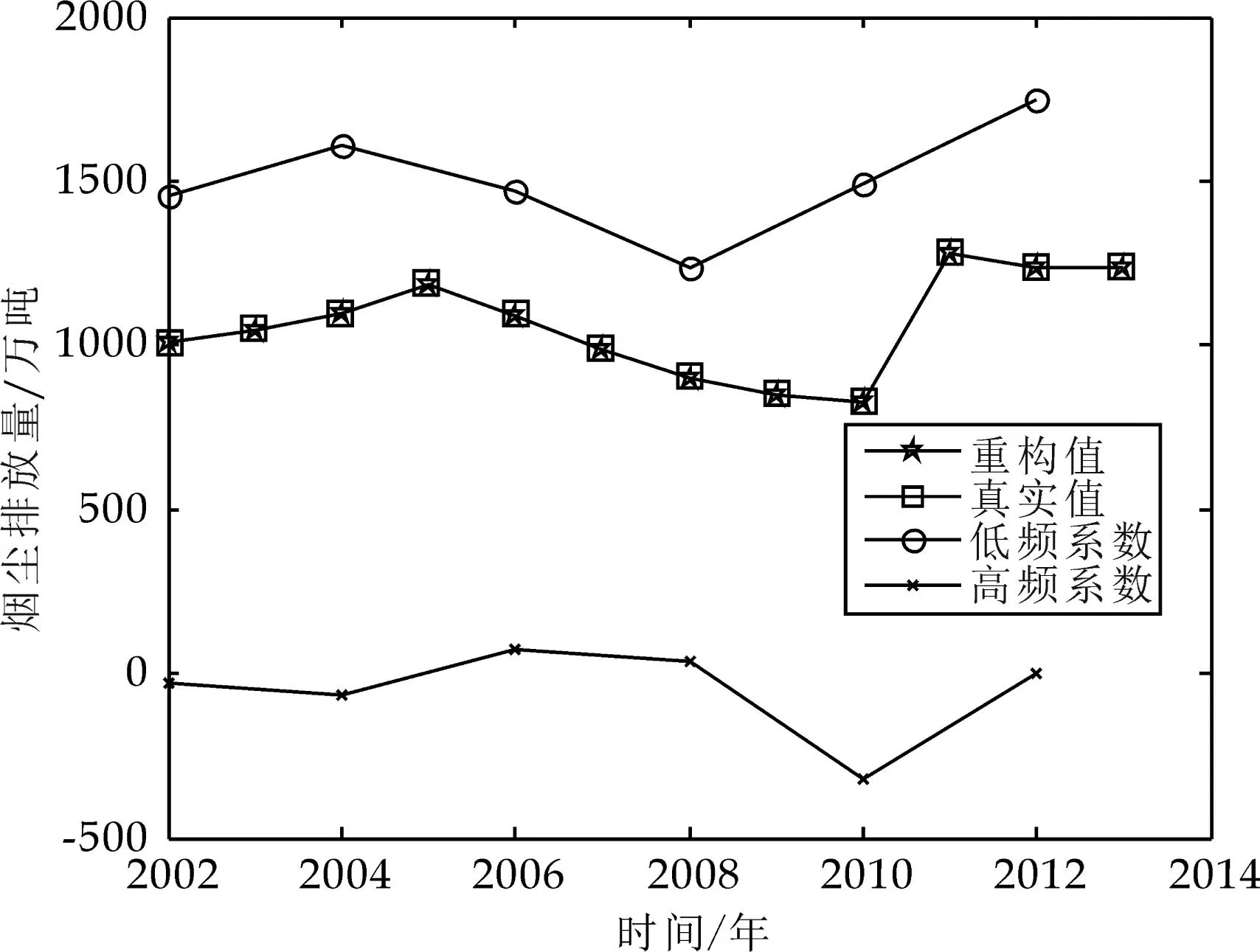
图3　烟尘排放量分解折线图

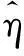
(5)

根据式(5)，得出二氧化硫排放量小波分解的误差平方和是1.447 6×10-24；烟尘排放量小波分解的误差平方和是1.809 5×10-25.由此可以得出结论：对于原先精确度只达到百分位的数据而言，小波分解重构基本不影响数据的精确程度.

采用MATLAB工具箱中的CFTOOL对cA二氧化硫与cA烟尘建立线性回归模型，得到两者的线性拟合方程如下：

L二氧化硫(t)=-19.68t+3 265

(6)

L烟尘(t)=24.68t+1 415

(7)

分别代入式(3)，即从各自的低频系数中减去各自的线性回归方程的预测值，使得到的数据整体的期望接近于零.然后，运用MATLAB中的线性拟合工具箱CFTOOL中的Fourier曲线拟合功能，选择式(4)作为预测模型，得到两者的Fourier拟合曲线.由于高频系数也是采用Fourier曲线拟合法，因此，在表3中给出了4个Fourier曲线的系数.

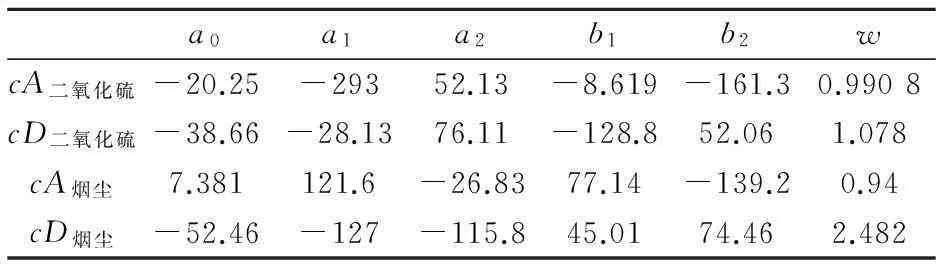
表3　四个Fourier拟合曲线的系数

运用拟合的曲线进行预测，然后进行逆变换，即可得到相应的二氧化硫排放量和烟尘排放量结果.经过曲线拟合之后，得到cA二氧化硫预测值为2 727.00，cD二氧化硫预测值为-2 01.97；cA烟尘预测值为1 633.88，cD烟尘预测值为-9.74.

运用小波分析逆变换，得到二氧化硫排放量的三个预测值为2 117.63、1 785.47、2 071.10.在小波分解时，分解的数据是11组，是奇数，由于小波变换的特性(将一个数据分成两部分，因此最后的合成也是两个数据合成一个数据.如果输入数据的数量是偶数，则高频系数将不是0)，所以得到的最后一个高频系数是0，相当于缺失.因此，对预测之后两个频道的数据进行重构的时候，有一个数据会接续之前的数据，即所得预测值的第一个数值和2012年的真实值是一致的.在此，不妨对这三者取平均值，得到的数值用以估计2013年的二氧化硫排放量，即预测得到的2013年的二氧化硫排放量是1 991.40；对烟尘排放量也采用二氧化硫排放量相同的处理方式，得到的三个预测值是1 235.77、1 148.44、1 162.21，最终得到2013年烟尘排放量的预测值是1 182.14.

结合侯琼煌和杨航分析结果[11]，两者的相对误差见表4所示.其中，相对误差用式(8)进行计算：

(8)

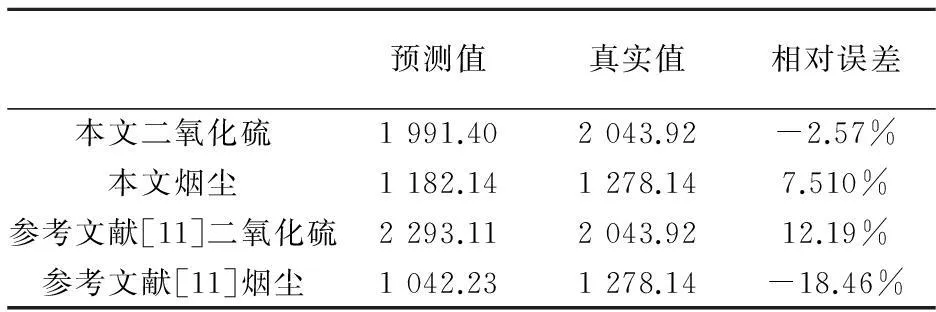
表4　预测结果与比较

从表4不难发现，本文与参考文献[11]比较可知:本文的预测方式拥有较高的精确度.

4分析

从表1我国对工业废气治理投资的数据可以看出，我国一直都比较重视废气治理，但2008～2012年的投放资金却没有跟上以前发展的趋势，因此导致了我国雾霾天气的加重.这也可以由图2和图3反映出来，我国二氧化硫的排放量在近年的下降趋势有所减缓，而烟尘排放量却有所升高；从两个回归方程式(6)和式(7)也能估算出，二氧化硫排放量每年只减少20万吨左右，相对于2 000万吨的基数来说非常少，而烟尘的排放量甚至呈每年近20万吨速度递增.

为了对我国废气治理投资情况进行分析，运用MATLAB的最小二乘法拟合函数polyfit，对我国2002～2007年在工业废气治理的投资数据建立模型，对于线性、二次函数、三次函数这三者而言，二次函数的误差最小，因此，假设工业废气治理投资在满足二次多项式的情况下，我国雾霾情况会有相当地好转，则我国从2008年来每年相差的投资是(万元)：30 325、535 737、1 269 595、2 105 547、2 255 563、217 191、-1 291 654，即从2008年到2012年，我国在废气治理上的投资稍显不足，但是在2013年，我国加大了有关于废气治理的投资.因此，我国在未来一段时间里，雾霾情况会有所好转，二氧化硫排放量的下降速度会加快，烟尘排放量也会从每年不确定的波动转向逐年递减.

5结束语

本文运用小波分析的多维度特点，将我国雾霾天气产生源头之一的工业废气分解到两个频道，分别建立模型进行预测，充分考虑了雾霾预测的非线性特性.运用Fourier曲线的周期特性进行拟合，得到了较精确的预测效果，得出了我国正逐渐加大对雾霾治理力度的结论.我国的雾霾情况未来几年会有所好转，空气中二氧化硫的含量会逐年递减，而粉尘的含量也会从波动转向递减.本文为雾霾短期预测提供了一种新的预测方法，为科学决策提供了智力支撑.

参考文献

[1] 孙亮.灰霾天气成因危害及控制治理[J].环境科学与管理，2012,37(10)：71-75.

[2] 潘本锋,汪巍,李亮,等.我国大中型城市秋冬季节雾霾天气污染特征与成因分析[J].环境与持续发展，2013(1)：33-36.

[3] 王勇,刘严萍,李江波,等.水汽和风速对雾霾中PM2.5/PM10变化的影响[J].灾害学，2015,30(1)：5-7.

[4] 郭庆春,何振芳，李力.西安市空气污染指数的神经网络预测模型[J].河南科学，2011,29(7)：863-868.

[5] 艾洪福,石莹.基于BP人工神经网络的雾霾天气预测研究[J].计算机仿真，2015,32(1)：402-405.

[6] 白鹤鸣,沈润平,师华定,等.基于BP神经网络的空气污染指数预测模型研究[J].环境科学与技术，2013,36(3)：186-189.

[7] 王坤龙.天津地区雾霾的成因及预测模型建立的研究[J].天津职业院校联合学报，2014,16(8)：25-29.

[8] 杨云,付彦丽.基于T-S模型模糊神经网络的PM2.5质量浓度预测[J].陕西科技大学学报(自然科学版)，2015,33(6):162-166.

[9] 刘杰,杨鹏,吕文生,等.基于气象因素的PM2.5质量浓度预测模型[J].山东大学学报(工学版),2015,45(6):76-83.

[10] 石灵芝,邓启红,路婵.基于BP人工神经网络的大气颗粒物PM10质量浓度预测[J].中南大学学报(自然科学版),2012,43(5):1 969-1 974.

[11] 侯琼煌,杨航.基于三次指数平滑模型的雾霾天气分析与预测[J].环境保护科学，2014,40(6)：73-77.

[12] 王海鹏,张斌,刘祖涵,等.基于小波变换的兰州市近十年空气污染指数变化[J].环境科学学报，2011,31(5)：1 070-1 076.

[13] 朱希安,金声震,宁书年,等.小波分析的应用现状及展望[J].煤田地质与探勘，2003,31(2)：51-55.

[14] 徐科,徐金梧,班晓娟.基于小波分解的某些非平稳时间序列预测方法[J].电子学报，2001,29(4)：566-568.

[15] 葛哲学,陈仲生.Matlab时频分析技术及其应用[M].北京：人民邮电出版社,2006.

[16] 中华人民共和国国家统计局.中国统计年鉴2014[M].北京：中国统计出版社，2014.

【责任编辑：晏如松】

The haze weather analysis and prediction based on the wavelet analysis

YANG Wen-guang1, LIN Lian-hai1, TIAN Li-qin2

(1.Department of Basic Course, North China Institute of Science and Technology, Sanhe 065201, China; 2.College of Computer, North China Institute of Science and Technology, Sanhe 065201, China)

Abstract:With the development of Chinese society,fog and haze have become a common environmental disaster.The sulfur dioxide emissions,soot emissions and China′s annual investment funds on industrial waste gas treatment from 2000 to 2013 is used for forecasting.The sulfur dioxide emissions and soot emissions data is decomposed to two different frequency channels by wavelet analysis.According to the periodicity of data to establish prediction model,and forecast China′s future haze situation. In order to analyze the future haze weather conditions,a linear model for China′s annual investment funds on industrial waste gas treatment was built.The prediction results show that the Chinese waste gas investment is slightly less in recent years.The sulfur dioxide pollution will reduce in the future,but the soot pollution will increase slightly.Therefore,it is necessary to increase the investment for waste gas treatment.

Key words:haze weather; wavelet analysis; industrial waste gas; forecast

中图分类号：X701

文献标志码：A

文章编号：1000-5811(2016)03-0166-05

作者简介:杨文光(1981-)，男，河北涞水人，讲师，硕士，研究方向：模糊系统与神经网络

基金项目：国家自然科学基金项目(61472137)； 华北科技学院重点学科资助项目(HKXJZD201402)； 华北科技学院教学研究资助项目(HKJYZD201565)

收稿日期:2016-01-24