甘肃礼县某矿区工程独立坐标系的建立方法及过程

朱建华，龚真春，白　冰，陈金龙（61243部队,甘肃　兰州　730020）



甘肃礼县某矿区工程独立坐标系的建立方法及过程

朱建华，龚真春，白冰，陈金龙
（61243部队,甘肃兰州730020）

摘要：工程测量对长度变形控制很严格，一般要通过建立独立坐标系来限制其长度变形。采用抵偿高程面的方法建立独立坐标系在实际应用中较为广泛，比较了抵偿高程面坐标系实现的常用形式及适用范围。结合甘肃礼县某矿区工程实例，给出了该矿区独立坐标系建立的详细过程、计算方法和结果，以供实际应用参考。

关键词：长度变形；抵偿高程面；独立坐标系；计算方法

在城市或工程建设地区（如矿山）布设测量控制网时，其成果不仅要满足大比例尺测图的需要，还要满足一般工程放样的需要,要求由控制网坐标反算出的长度与实测的长度尽可能相符。《工程测量规范》和《城市测量规范》中规定长度变形不大于2.5cm/km（相对误差1/40000），甚至更小。但国家坐标系统在许多情况下不能满足这一要求,这就需要通过建立独立坐标系以控制长度变形[1]。控制长度变形的方法有多种，如建立抵偿高程面坐标系、平移中央子午线、建立基于工程椭球独立坐标系等[2，3]。本文结合承担的甘肃礼县某矿区工程测量任务，就采用抵偿高程面的方法建立独立坐标系，从控制变形精度、测区特点及控制范围等方面进行分析与比较，针对该矿区实际情况，给出了其详细的计算过程与结果。

1　长度变形分析及计算公式

由于地面方向值改正数（三差改正）较小，在等级低于三等的三角和导线测量中一般不加改正，而主要考虑的是按高程归化和高斯投影长度变形对边长带来的影响[4]。

众多的文献资料已给出了高程归化和高斯投影长度变形的详细推导过程。下面直接给出高程归化改正和高斯投影长度变形计算公式。如图1所示。令高程归化改正数为，则有：

式中：Hm为测区平均高程面相对于大地水准面的高程；hm为大地水准面至参考椭球面的高程；D为测区平均高程面上的水平距离；Rm为参考椭球面在测区内的平均曲率半径。

图1　地面长度化算示意图

将参考椭球上的长度归算到高斯平面上，令其改正数为△S，则有：

式中：S为在参考椭球面上的长度；ym为高斯平面上的横坐标值。

由式（1）和式（2）可知高程归化改正数△D恒为负值，其绝对值与归化高程成正比；高斯投影长度改正数△S恒为正值，与高斯平面上的横坐标值的平方成正比[5]。

由上述可得出，地面边长观测值经高程归化和高斯投影改正所引起的长度变形值为：

因△D较小，故令S=D，则根据（1）式和（2）式有：

要求长度变形不大于2.5cm/km，即有：

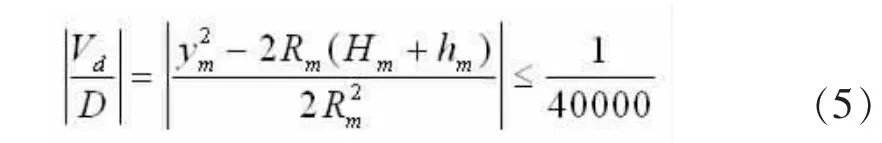
对于一定的测区，Rm为定值，因此，长度变形是否小于2.5cm/km，主要取决于测区横坐标值ym和归化高程（Hm+hm），即取决于所选用的坐标系和高程系。

2　抵偿高程面坐标系实现方式的比较

基于抵偿高程面建立独立坐标系常用方法主要有：一般形式、任意带坐标系和投影于抵偿高程面的任意带坐标系三种。

2.1一般形式

它采用国家统一的分带高斯投影，其中央子午线与国家坐标系一致，用人为改变归化高程来使它与高斯投影的长度改化相抵偿，即通常所称的抵偿高程面的高斯正形投影3o带平面直角坐系。此方法的关键是求出抵偿面高程。其优点是计算简单，投影中心精度高；不足是在投影中心东西两侧，投影精度衰减迅速，超过中心东西10km外，精度则很难达到1/40000的要求。适用于测区面积不大（一般小于100km2）、测区为南北走向的丘陵地貌的测区。其在各种小区域工程测量中应用非常广泛[6]。

2.2任意带坐标系

其中央子午线不再与国家坐标系保持一致，而是根据实际情况选择一条经线作为中央子午线，长度的高程归算面仍为国家参考椭球面。其优点是投影中心精度高、能满足投影精度的范围广（投影中心东西45km都能达到1/40000的精度）;缺点是对地形起伏较大的地貌，个别区域投影精度较差。适用于测区面积大、地形相对平坦的各种区域[7]。

2.3投影于抵偿高程面的任意带坐标系

其中央子午线以及长度的高程归算面均与国家坐标系不同。这种坐标系将抵偿系和任意带二者的优点结合起来，以期获得在较大区域长度变形仍能满足规范要求，适应现代城市规模不断扩大、城市面积不断扩张的需求[8]。

3　采用一般形式建立矿区独立坐标系过程

根据上述基于抵偿高程面建立独立坐标系的分析比较，结合矿区地形特点及控制面积（详见工程实例），下面给出采用一般形式建立独立坐标系的详细步骤。

3.1计算测区中心附近起算的横坐标

由于高程归化改正数△D恒为负值，而高斯投影长度改正数△S恒为正值的特点，两种改正数具有相互抵消的可能。当△S=△D时，两种改正相互抵消，即有：

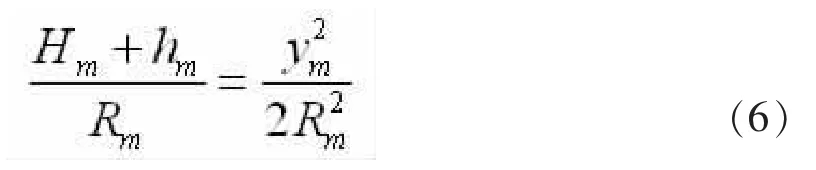
取Rm≈6371km，代入上式有：

将测区的归化高程（Hm+hm）代入，可求得长度变形为零处的ym值，为了求得该点经差，考虑高斯投影公式：

只取上式一次项，并令，均N=6371km，p,l均以分为单位，则：

ym=1.853×lcosB

同理，可得：

式中：ym为测区中心附近起算的横坐标；l为测区中心附近中央子午线的经差；B为测区中心的纬度。

3.2变形计算

计算时的S取值为1000m，意即每公里的变形值。

3.3测区中心相对于抵偿高程归化面的高程

3.4抵偿高程面相对于参考椭球面的高程

式中：（Hm+hm）为测区平均高程面。

3.5缩放系数计算

3.6国家坐标系同独立坐标系间的转换

由国家坐标系转换为独立坐标系的公式为：

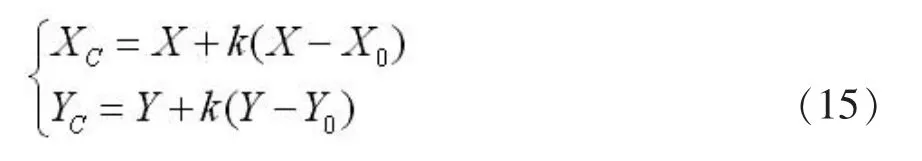
由独立坐标系转换为国家坐标系的逆变换公式为

式中：X，Y为国家统一坐标系中的坐标；XC，YC为独立坐标系的坐标；X0，Y0为缩放原点，可选在测区中心的整数值或控制点[9]。

4　工程实例计算与分析

甘肃礼县某矿区测量任务位于偏远山区，地势北高南低，矿区范围约35km2，海拔2600～3300m，前期由甲方完成矿区33个GNSS点位的选埋工作。依据技术规程要求，现场作业时，先利用GNSS测量方式获取33个点位的1980年西安坐标系成果，后按上述一般形式建立矿区独立坐标系，求出矿区独立坐标系成果。成果提交时，甲方专门组织人员于实地进行距离观测，以验证长度变形是否满足要求及后期施工放样需要。实地详细计算为：

1）矿区平均高程取（Hm+hm）2834m，Rm＝6371km，中央子午线为105°；测区中心L＝104°27'37，纬度B＝34°27'，l=33'；按3°带投影。

2）矿区最远点距中央子午线距离按（9）式计算得：ym=1.853×33×cos(34°27')=50.423km。

3）抵偿前的最大变形δ按式（11）计算得：

δ=-1000×2834/6371000+1000×504232/(2×63710002) ＝-0.4135088m。大于限差规定，不满足要求。

4）矿区平均高程面相对于抵偿高程面的高程，按式(12)计算得：

HC＝504232/(2×6371000)＝199.54m。

5）抵偿高程面相对于参考椭球面的高程按式（13）计算得：H0＝2834－199.34＝2634.46m。

6）缩放系数按式（14）计算得：

k=2634.46/6371000＝0.000413508。

7）抵偿后的最大变形δ按式（11）计算得：

δ=-1000×199.54/6371000+1000×504232/(2×637 10002)＝-0.03132004＋0.03131931=-0.00000073m。

抵偿后的最大变形同理论相符，即实现了将长度变形控制在一个微小的范围,使计算出来的长度在实际利用时不需要作任何改算，可忽略不计。

8）国家80坐标系同矿区独立坐标系的转换由式（15）计算可得，缩放原点为控制点ZS20。表1列出计算结果的一部分，其中实测边长由甲方使用全站仪测量所得。由表1及上述抵偿后最大变形-0.00000073m可看出，独立坐标反算出的边长与实测边长的较差均小于2.5cm/km限差规定，符合技术规程要求和后期工程测图及施工放样需求。

表1　1980年西安坐标系（3°带）成果转换为独立坐标系成果/m

5　结束语

限制长度变形是城市测量、大比例尺及精密工程测量中所要进行的一项工作，控制长度变形有多种方法。采用抵偿高程面坐标系是应用较为广泛的一种方法，其常用的三种实现形式都能与国家统一坐标系相互转换，且转换关系简便。在具体使用时，要针对测区地形特点和控制范围，选择合适的实现方式，以满足作业需求。

参考文献：

[1]张正禄.工程测量学[M].武汉:武汉大学出版社,2005.

[2]张述清,李永云.地方独立坐标系统的建立及其实现[J].测绘工程,2007,16(4):22-24.

[3]陈士银.建立地方独立坐标系的方法[J].测绘通报1997, (10):5-6.

[4]瞿翊,付子傲,蒋理兴.地籍测量[M].北京:放军出版社,2000.

[5]孔祥元,郭际明,刘宗泉.大地测量学基础[M].武汉:武汉大学出版社,2009.

[6]谢玉兵,张丽萍.各种抵偿高程面坐标系统的比较及应用分析[J].测绘科学与工程,2013,33(6):12-13.

[7]兰京京,孙清娟.几内亚BOKE588铝土矿勘探独立坐标系的建立及转换研究[J].测绘与空间地理信息,2012,35 (3):196-197.

[8]雷伟伟,姜斌.国家坐标系与城市坐标系转换方法的探讨[J].测绘科学,2010,35(1):16-17.

[9]薛晓轩,鲁彩娟,秦闻宇.城市坐标系的选择与抵偿计算[J].测绘与空间地理信息,2010,33(4):188-189.

中图分类号：P209