大跨度铁路连续钢桁梁桥预拱度设置研究

冯　沛

(铁道第三勘察设计院集团有限公司，天津　300142)



大跨度铁路连续钢桁梁桥预拱度设置研究

冯沛

(铁道第三勘察设计院集团有限公司，天津300142)

摘要：通过实际工程应用，对大跨度连续钢桁梁桥预拱度的设置方法进行研究。采用几何法建立上弦杆杆件调整值与下弦杆节点位移的影响矩阵，然后建立上弦杆调整值与预拱度的函数方程，通过求解多元约束条件方程组，得出合适的上弦杆调整值。几何法仅是杆件的几何关系，与受力无关，与预拼装过程一致，偏差小；并且建立影响矩阵方便，无需借助有限元计算；影响矩阵小，每跨可以单独计算，互不影响，提高收敛和计算速度；给出一种较为简单的预拱度设置方法，大大简化预拱度设置工作并经过工程验证是正确的。

关键词：铁路桥；连续钢桁梁；预拱度；几何法；影响矩阵

1概述

为保证列车过桥时桥上线路转角应尽可能小，使列车能比较平顺地通过桥梁，因此需要设置预拱度。对于大跨度高速铁路桥梁，预拱度的设置尤其重要。对于整体节点钢桁梁结构，一般是通过调整弦杆杆件长度来达到结构起拱的目的。对于简支钢桁梁，为了简化制造和安装工作，设计时是让下弦杆和腹杆的长度均保持不变，而只让上弦杆的理论长度伸长的方法进行设置。并且假定其预拱度曲线为圆形，上弦杆调整值都相同，然后试算得到合适的上弦杆拼接缝值；对于连续钢桁梁，中支点处需设置反向曲线使连续梁各跨预拱度匀顺衔接，其上弦杆调整值有正值或者负值的出现，并且为使厂设预拱度与理论拱度接近，部分杆件不伸长也不缩短。因此，对于连续钢桁梁来说，其上弦杆的调整值是不同的，并且预拱度曲线并没有一个解析解，只能通过试算得到合适的上弦杆调整值，要求厂设预拱度与理论预拱度值的差值在合理的可接受范围之内，因此连续钢桁梁结构杆件的调整值并不是一个唯一解。

对于较为复杂且跨度较大的连续钢桁梁结构，一般是通过某种方法建立杆件的调整值与预拱度值的函数关系，然后建立多元约束条件方程组，通过求解方程得到合适的杆件调整值。目前已经发表的文献中，均是采用升降温法来调整弦杆的长度达到设置预拱度的方法[2-4]。但其存在以下问题：(1)杆件是受力变形，是在有应力状态下的调整值，而杆件的预拼装是在无应力状态下进行的，会造成偏差的增大；(2)需通过有限元计算分别得到每根上弦杆杆件单位调整值与下弦杆节点位移、支座节点反力的影响系数矩阵，当结构较大时工作量很大，且影响系数矩阵非常庞大，造成求解时间增长。

本文采用几何法建立上弦杆杆件单位调整值与下弦杆节点位移的影响矩阵，通过求解多元约束条件方程组，得出合适的上弦杆调整值，给出了一种较为简单的预拱度设置方法。为验证本文方法的正确性，采用BIM软件完全按照预拱度数值建立了三维模型，对杆件进行了拼装模拟。

2预拱度设置方法

几何法为采用简单的几何关系，建立上弦杆调整值与下弦节点挠度之间的关系。如图1所示，当节点中心两侧上弦杆的第一排螺栓孔的起线各增大Δ时，则梁端将下降。若将下降值累积在节点中心的一侧，B端不降低，则D端下降值δ可按照几何关系求出[5]。

图1　预拱度与上弦杆调整值几何关系

由图1可得

(1)

式中，d为节间长度。

因角度θ值很小，所以，sinθ≈θ

故

(2)

由图形AEC，近似地 2Δ1≈θ·AE=θ·H

即

(3)

由式(2)、式(3)得

(4)

根据几何关系，下一个节点下降值为2δ1，依此类推。由此可建立任一上弦杆伸长值对下弦杆挠度值的影响矩阵。

采用非线性规划方程，目标函数为计算挠度值与理论挠度值的差值平方和最小，约束条件可为各点计算挠度值与理论挠度值的差值在合理范围内，未知量即为各上弦杆的伸长值。

目标函数

(5)

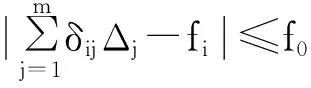
式中fi——第i个下弦节点理论预拱度值；

δij——第i个下弦节点在第j根上弦杆单位伸长量产生的竖向位移；

Δj——第j个上弦杆的伸长值；

f0——理论预拱度与厂设预拱度的差值。

可以通过设置更多的约束方程以取得更好的结果，例如Δj为偶数；需调整杆件数尽可能少，且调整数值大小尽量统一；相邻杆件调整值的差值限定值；实际预拱度与理论预拱度差值限定值等。

此方法有如下优点：(1)与受力无关，仅是杆件的几何关系，与预拼装过程一致，偏差小；(2)建立影响矩阵方便，无需借助有限元计算，并且仅用建立上弦杆伸长量与下弦杆节点挠度的影响矩阵；(3)矩阵小，每跨可以单独计算，互不影响；并且每跨一般对称设置预拱度，因此其上弦杆伸长值也为对称设置，这样影响矩阵可减少一半，提高收敛和计算速度。

3工程应用

济南黄河公铁两用桥为石济铁路客运专线工程、邯济线铁路扩能改造工程及济南市“北跨”城市空间发展向北跨越黄河通道的公铁合建桥梁，共承担四线铁路荷载及6车道公路荷载。其中下层铁路为石济客专及邯济、胶济联络线铁路左、右线，上层公路为双向6车道公路。采用(128+3×180+128)m刚性悬索加劲连续钢桁梁结构，3片主桁，桁中心距14.65m，桁高15m，桁式为有竖杆三角形桁式，整体节点，节间长度12.8～13m。上下桥面系均为正交异性钢桥面板结构，其立面如图2所示。某杆件节点编号如图3所示。

图2　济南黄河公铁两用桥立面(单位：cm)

图3　济南黄河公铁两用桥杆件节点编号

由于该桥为高速铁路桥梁，且为双层桥面，跨度大，预拱度的设置对行车平顺性以及钢桥面的焊接、整体节点的杆件拼接等都有较大的影响。按照上述方法，计算得到上弦杆的调整值如表1、表2所示。厂设预拱度值与理论预拱度差值如表3、表4所示。

表1　边跨上弦杆调整值　mm

表2　1/2主跨上弦杆调整值　mm

表3　1/2主跨计算预拱度值　mm

通过表3、表4可以看出，厂设预拱度与理论预拱度吻合较好。

本文通过BIM软件建立了三维模型对杆件进行了预拼装，对预拱度设计进行了验证，如图4所示。目前本桥正在施工当中，首孔钢梁已经顺利通过试拼装，验证了本文方法的正确性。

表4　边跨计算预拱度值　mm

图4　济南黄河公铁两用桥三维模型

4结论

本文采用几何法建立上弦杆杆件单位调整值与下弦杆节点位移的影响矩阵，通过求解多元约束条件方程组，得出合适的上弦杆调整值，给出了一种较为简单的预拱度设置方法，有如下优点。

(1)本方法与受力无关，仅是杆件的几何关系，与预拼装过程一致，理论预拱度与实设预拱度偏差小。

(2)建立影响矩阵方便，无需借助有限元计算，并且仅需建立上弦杆伸长量与下弦杆节点挠度的影响矩阵。

(3)矩阵小，每跨可以单独计算，互不影响；并且每跨一般对称设置预拱度，因此其上弦杆调整也为对称设置，这样影响矩阵可减少一半，提高收敛和计算速度。

参考文献：

[1]中华人民共和国铁道部.TB 1002.2—2005铁路桥梁钢结构设计规范[S].北京：中国铁道出版社，2005.

[2]胡步毛，艾宗良，袁明，等.基于非线性规划实现钢桁连续梁预拱度[J].铁道工程学报，2010(4):49-52.

[3]曾永平，陈天地，袁明，等.大跨度铁路钢桁梁斜拉桥预拱度设置[J].铁道工程学报，2010(10):78-81.

[4]西南交通大学.铁路钢桥[M].北京：人民铁道出版社，1978.

[5]武芳文，薛成凤，赵雷.连续刚构桥梁悬臂施工线形控制分析[J].铁道工程学报，2006(7)：29-33.

[6]吴冲.现代钢桥[M].北京：人民交通出版社，2006.

[7]马亮，王天鹏.现行几种预拱度计算设置方法的比较[J].北方交通，2006(7)：44-46.

[8]程翔云.悬臂施工中的预拱度设置[J].公路，1995(7)：9-11.

[9]孙英杰，肖海珠，徐伟.郑州黄河公铁两用桥施工控制关键技术研究[J].桥梁建设，2011(2)：5-8.

[10]李杰，陈淮，刘建.郑州黄河公铁两用桥主桥第一联顶推施工控制分析[J].施工技术，2011，40(17):11-15.

[11]董政，张鹏.郑州黄河公铁两用桥主桥钢桁梁支架拼装及顶推技术[J].铁道标准设计，2010(9):66-69.

[12]徐烨.天兴洲长江大桥钢桁梁预拼技术研究[J].铁道标准设计，2009(3):37-40.

Study on Camber-setting of Large Span Railway Steel Truss Bridge

FENG Pei

(The Third Railway Survey and Design Institute Group Corporation， Tianjin 300142， China)

Abstract：The method for camber-setting of large span railway steel truss bridge is studied with reference to engineering projects. Geometry method is adopted to establish the influence matrix between the adjustment value of the top chord and the displacement of the bottom chord node and then to obtain the equation between the adjustment value of top chord and the camber. The right adjustment value of the top chord is concluded by solving multiple constraint equations. Geometry method is only involved in the geometric relationship between the members， having nothing to do with stress and consisting with the process of preassembling with little deviation. The influence matrix of the equation is easy to be created without finite element calculation. The influence matrix is small and each span can be calculated separately without mutual interference， which improves the convergence and computation speed. A relatively simple method is presented in this paper for camber-setting， which greatly simplifies camber setting and proves applicable by engineering practices．

Key words：Railway bridge; Continuous steel truss beam; Camber; Geometry method; Influence matrix

中图分类号：U448.36

文献标识码：A

DOI:10.13238/j.issn.1004-2954.2016.04.015

文章编号：1004-2954(2016)04-0062-03

作者简介：冯沛(1983—)，男，工程师，2009年毕业于湖南大学桥梁与隧道工程专业，工学硕士，E-mail：fengpei@tsdig.com。

基金项目：铁道部科技研究开发计划项目(2011G012-A)

收稿日期：2015-08-17； 修回日期：2015-10-08