一类利用卷积定义的p叶解析函数类的系数边界
李 静
一类利用卷积定义的p叶解析函数类的系数边界
李 静
(江汉大学文理学院,湖北武汉430056)
卷积是研究解析函数的有效工具,对于解析函数的系数研究起到很大的作用.利用卷积定义了一类在单位圆盘U={z∈C:|z|<1}内的p叶解析函数类MDδ,pa,c(λ,b,α,β),利用正实部函数族的系数性质,得到了它的全体系数边界,同时推广了一些常用的结论.
卷积;算子;系数;星象函数;凸函数
1 预备知识
设A(p)表示单位圆盘U={z∈C:|z|<1}内具有泰勒级数
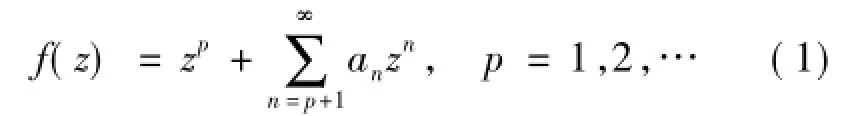

f(z)与g(z)的卷积定义为
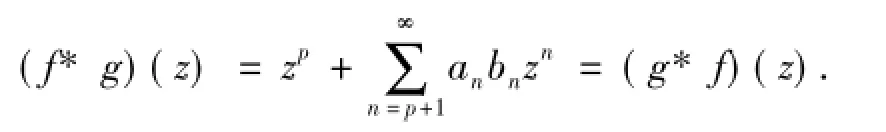
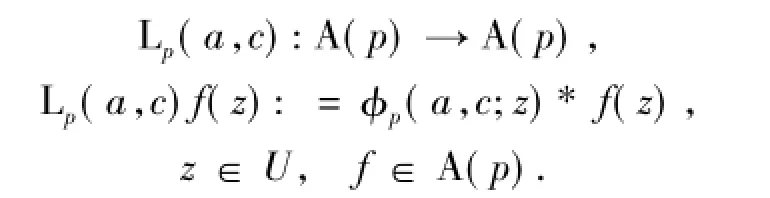
R.M.Goel等[2]定义了线性算子
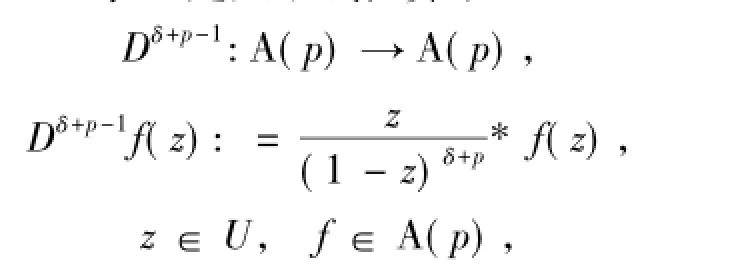
其中

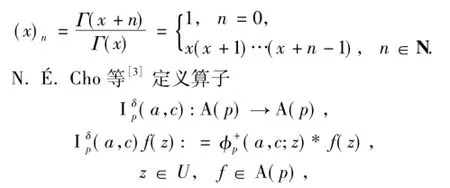
其中
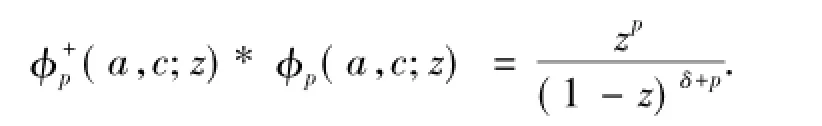
经计算得:
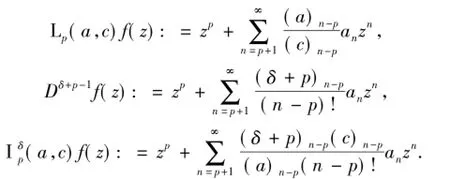
为了叙述方便,下文记
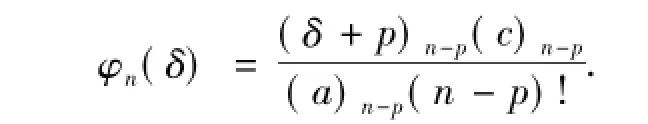
近期对于上述相关算子的研究,可以参看文献[7-16].另外,还注意到
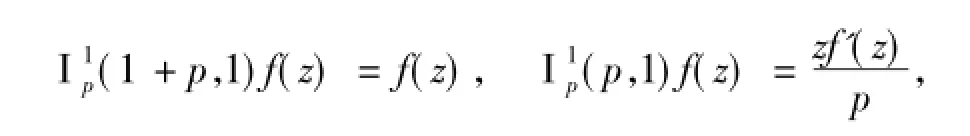
且
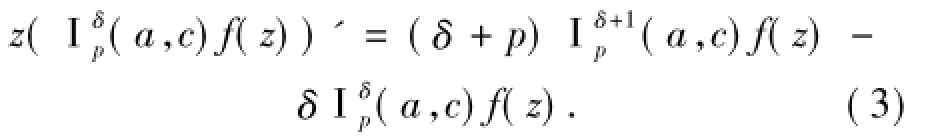
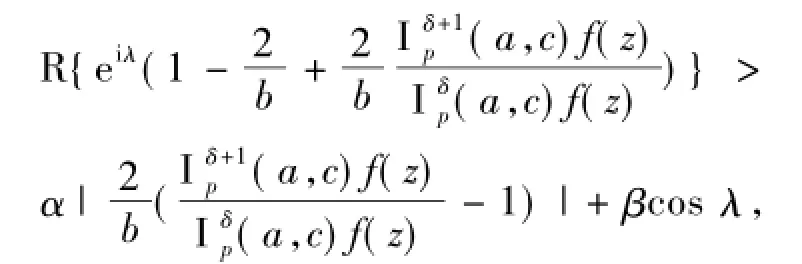
下面是一些特殊的函数类:
2 主要结论
引理1[23]若h(z)=1+c1z+c2z2+…(z∈U)为正实部解析函数,即Rh(z)>0,则|ck|≤2,k=1,2,….
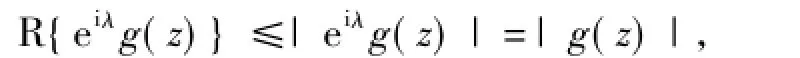
则

移项得

即

由于≤α≤β,易知0≤ξ<1,所以

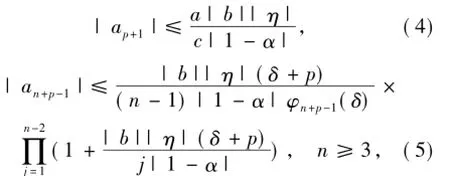
其中,η =(1-β)cos λ+i(1-α)sin λ.
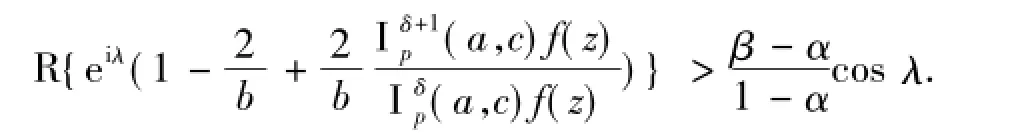
定义函数p(z)满足等式
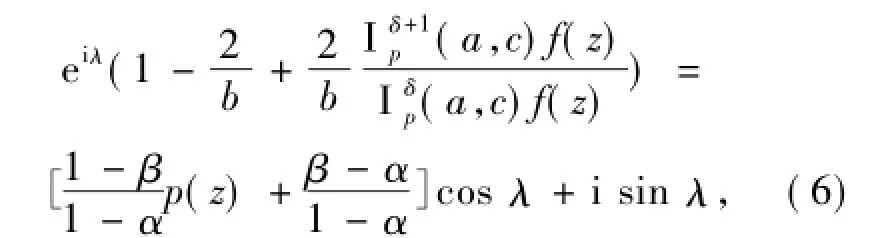
其中p(z)在U内解析且p(0)=1,Rp(z)>0.现记
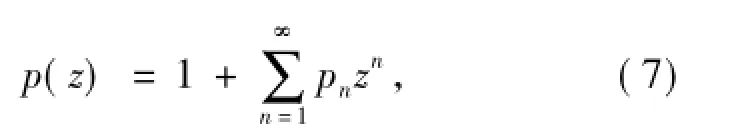
将(7)式代入(6)式得
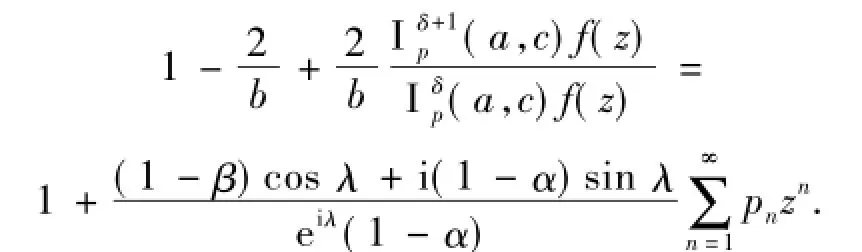
将上式进行变形得到
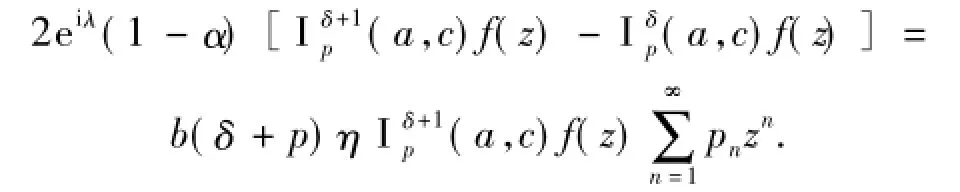
利用(3)式得

即
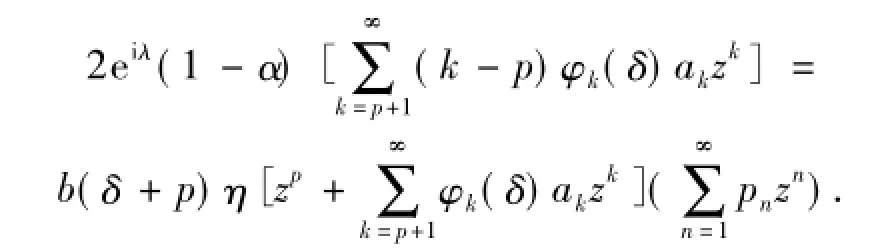
比较上式2边项zn+p-1的系数得
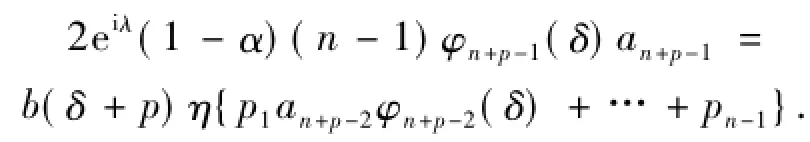
利用引理1得
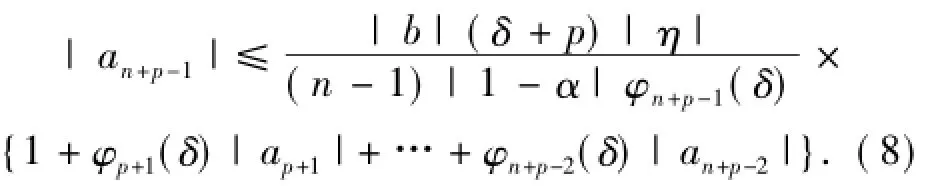
下面用数学归纳法证明结论.在(8)式中令n =2得
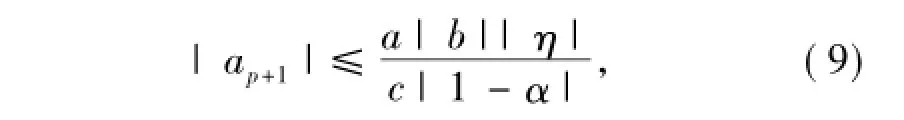
这就证明了(4)式.令n=3,并利用(9)式得
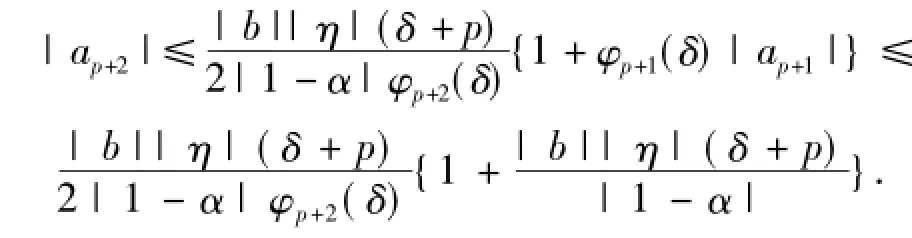
假设(5)式对n=k成立,即
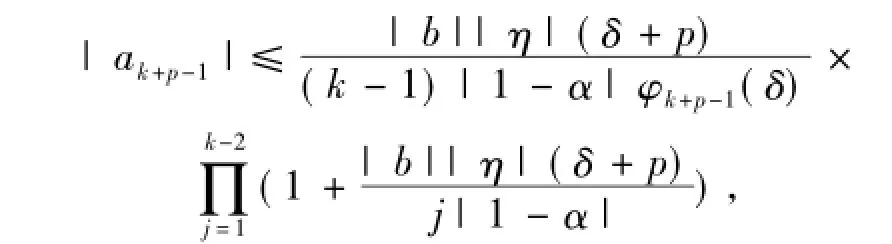
当n=k+1时有
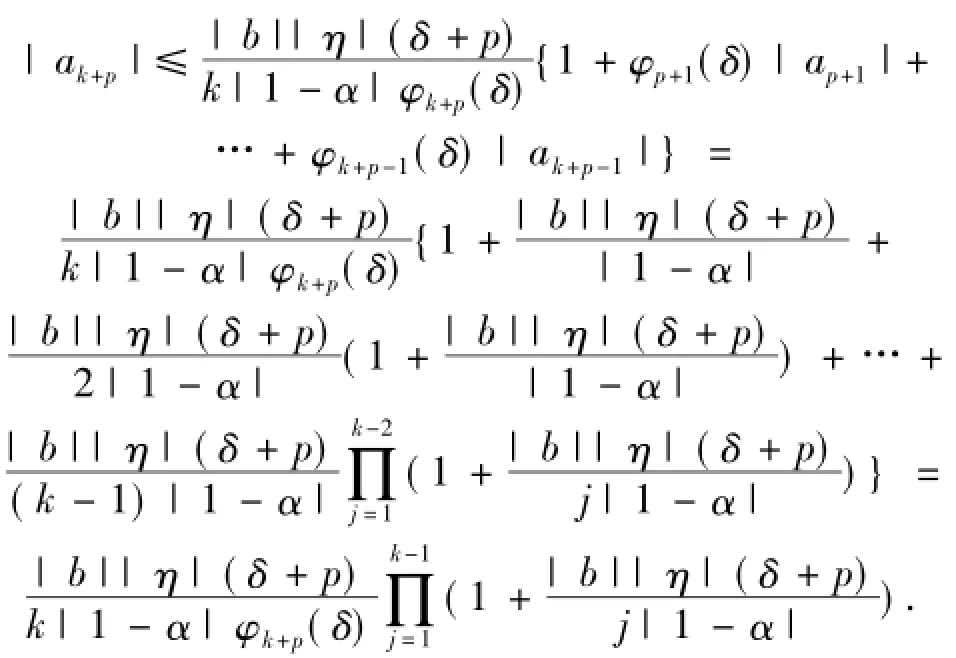
这就证明了(5)式.
推论1[19]设f(z)∈SD(α,β),则
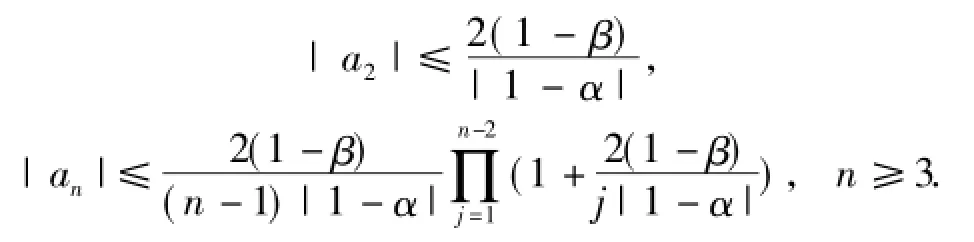
证明 在定理2中令a=c,δ=0,p=1,λ= 0,b=2.
推论2 设f(z)∈S*(β),则

证明 在推论1中令α=0.
推论3[20]设f(z)∈KD(α,β),则
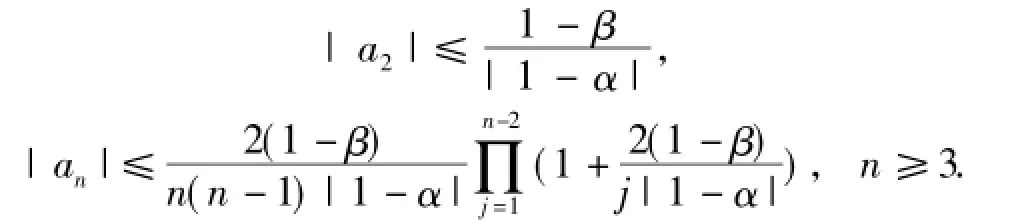
证明 在定理2中令a=c,δ=1,p=1,λ= 0,b=1.
推论4 设f(z)∈K(β),则

证明 在推论3中令α=0.
定理3 设f(z)∈A(p)由(1)式定义,若满足下面不等式
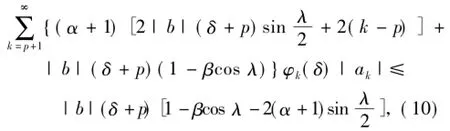
证明 为简便起见,记
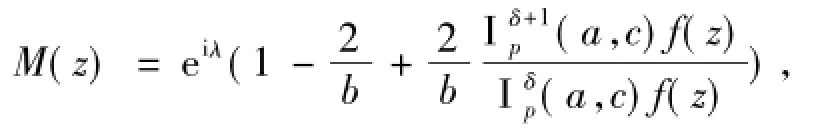
则要证明的结论即为

利用(3)式,经计算得
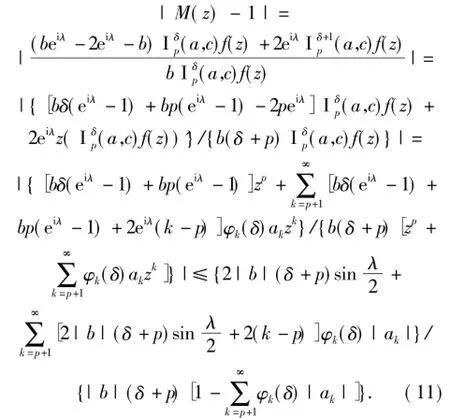
由于

所以
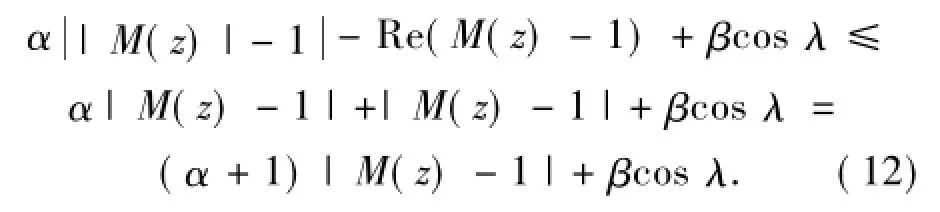
结合(11)式,如果(12)式的最后一个式子有上界1,即

上式经整理得
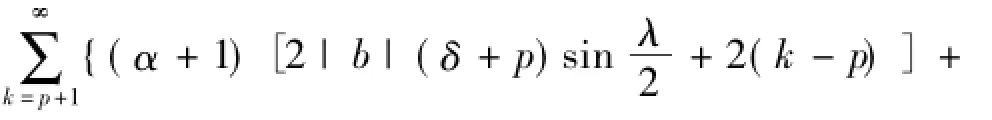
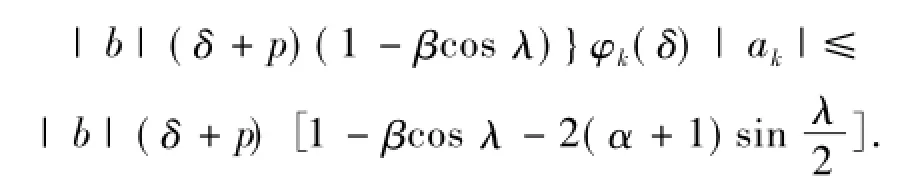
此式即为(10)式.此时由(12)式有
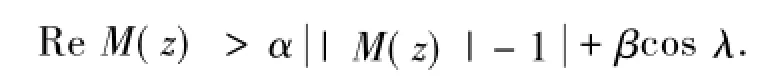
推论5[24]设f(z)∈A(p)由(1)式定义,若满足下面不等式
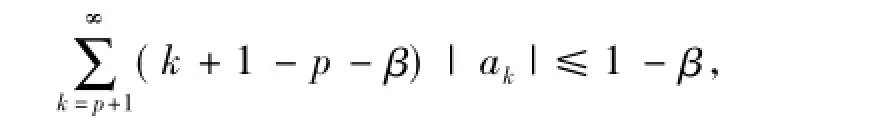
则f(z)∈Sp*(β).
证明 在定理3中令a=c,δ=-p+1,λ= 0,b=2,α=0.
推论6[25]设f(z)∈A(1)由(1)式定义,若满足下面不等式
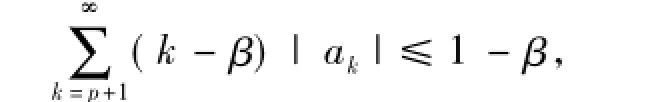
则f(z)∈S*(β).
证明 在推论5中令p=1.
推论7[24]设f(z)∈A(p)由(1)式定义,若满足下面不等式

则f(z)∈Kp(β).
证明 在定理3中令a=c,δ=-p+2,λ= 0,b=1,α=0.
推论8[26]设f(z)∈A(1)由(1)式定义,若满足下面不等式
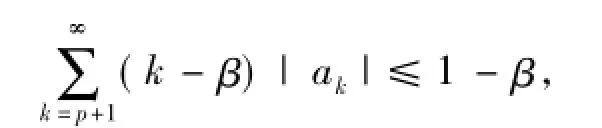
则f(z)∈S*(β).
证明 在推论5中令p=1.
[1]SAITOH H.A linear operator and its application of first order differential subordinations[J].Math Jpn,1966,44:31-38.
[2]GOEL R M,SOHI N.A new criterion for p-valent functions[J].Proc Am Math Soc,1980,78:353-357.
[3]CHO N ,KWON O S,SRIVASTAVA H M.Inclusion relationships and argument properties for certain subclasses of multivalent functions associated with a family of linear operator[J].J Math Anal Appl,2004,292(2):470-483.
[4]LIU J L,NOOR K I.Some properties of Noor integral operator[J].J Nat Geom,2002,21:81-90.
[5]NOOR K I,ARIF M.Generalized integral operators related with p-valent analytic functions[J].Math Inequal Appl,2009,12(1):91-98.
[6]NOOR K I.On new classes of integral operators[J].J Nat Geom,1996,16:71-80.
[7]SRIVASTAVA H M,GABOURY S.A new class of analytic functions defined by means of a generalization of the Srivastava-Attiya operator[J].J Inequal Appl,2015,39:1-15.
[8]刘文娟,彭娟,杨清.与Noor积分算子有关的多叶解析函数子类的性质[J].扬州大学学报(自然科学版),2012,15(3):8-11.
[9]吴春.全纯函数差分算子的值分布[J].四川大学学报(自然科学版),2015,52(6):1-6.
[10]SEOUDY T M,AOUF M K.Inclusion properties for some subclasses of analytic functions associated with generalized integral operator[J].J Egyptian Math Soc,2013,21(1):11-15.
[11]XU Q H,XIAO H G,SRIVASTAVA H M.Some applications of differential subordination and the Dziok-Srivastava convolution operator[J].Appl Math Comput,2014,230:496-508.
[12]秦川,李小飞.一类利用复合算子函数定义的解析函数类的包含性质[J].四川师范大学学报(自然科学版),2015,38(3):376-340.
[13]田琳,韩红伟.算子解析函数的系数不等式[J].数学的实践与认识,2014,44(18):239-245.
[14]李书海,汤获,马丽娜,等.与条形区域有关的解析函数新子类[J].数学物理学报,2015,35(5):970-986.
[15]张兆霞,刘名生.涉及Dziok-Srivastava算子的某些多叶解析函数子类的性质[J].华南师范大学学报(自然科学版),2013,45(3):37-41.
[16]鲍春梅.由线性算子定义的解析函数子类的Fekete-Szego不等式[J].数学的实践与认识,2014,44(19):292-296.
[17]ARIF M.On certain suffciency criteria for p-valent meromorphic spiralike functions[J].Abs Appl Anal,2012,1:1-9.
[18]ROBERTSON M S.Univalent functions f(z)for wich zf'(z)is spirallike[J].Michigan Math J,1969,16:97-101.
[19]OWA S,POLATOGLU Y,YAVUZ E.Coefficient inequalities for classes of uniformly starlike and convex functions[J].J Inequal Pure Appl Math,2006,7(5):1-6.
[20]SHAMS S,KULKARNI S R,JAHANGIRI J M.Classes of uniformly starlike and convex functions[J].Int J Math Math Sci,2004,55:2959-2961.
[21]RAVICHANDRAN V,SELVARAJ C,RAJGOPAL R.On uniformly convex spiral functions and uniformly spirallike function[J].Soochow J Math,2003,29(4):392-405.
[22]LATHA S.Coefficient inequalities for certain classes of ruscheweyh type analytic functions[J].J Inequal Pure Appl Math,2008,9(2):1-5.
[23]POMMERENKE C H.Univalent Functions[M].Gotingen:Vandenhoeck and Rupercht,1975.
[24]MUHAMMAD A,JANUSZ S,MAHAMMAD A.Coefficient inequalities for a subclass of p-valent analytic functions[J].The Scientific World J,2014,2014:1-5.
[25]MERKES E P,ROBERTSON M S,SCOTT W T.On products of starlike functions[J].Proc Am Math Soc,1962,13:960-964.
[26]SILVERMAN H.Univalent functions with negative coeffcients[J].Proc Am Math Soc,1975,51:109-116.
Coefficient Bounds for a Subclass of p-valent Analytic Functions by Convolution
LI Jing
(College of Arts and Sciences,Jianghan University,Wuhan 430056,Hubei)
Convolution is an effective tool to study analytic functions,which plays a significant role in the study of the coefficient of analytic functions.In this paper,a subclass(λ,b,α,β)of p-valent analytic functions defined by convolution in the open disc U ={z∈C:|z|<1}is introduced.The aim of the paper is to study all coefficient bounds of the above class with coefficient properties of real part functions.Many known results are generalized.
convolution;operator;coefficient;starlike function;convex function
O174.51
A
1001-8395(2016)05-0686-05
10.3969/j.issn.1001-8395.2016.05.013
(编辑 余 毅)
2015-09-25
湖北省教育厅规划课题(2014B354)
李 静(1984—),女,讲师,主要从事应用数学的研究,E-mai:2935788547@qq.com
2010 MSC:30C45

