2.5D结构筒状立体机织物细观分析及建模
邵明正
(天津工业大学复合材料研究所,天津 300387)
2.5D结构筒状立体机织物细观分析及建模
邵明正
(天津工业大学复合材料研究所,天津 300387)
文章为了探究2.5D结构筒状立体机织物的细观几何关系,通过显微观察和结构分析,提出纬纱截面为双凸透镜截面、经纱截面为扇形截面的假设,并建立了2.5D结构筒状立体机织物实体模型和2.5D结构细观几何结构模型,推导了细观几何表达式和细观微元中纤维体积分数计算公式。结果表明2.5D结构被用于筒状织物时,细观几何结构会发生一些改变。
筒状立体机织物;2.5D结构;细观几何模型。
1 前言
筒状复合材料结构件是在工程中常用的基本构件,使用筒状织物作为增强体,若采用高性能纤维(如碳纤维、芳纶纤维)进行增强体织造,则使构件具有轻质、高比强、耐疲劳、耐腐蚀等优越性能。目前,筒状复合材料构件已用于生产结构支架、输送管道、衬套、罩体、超耐高温隔热管等产品,在航空航天、化学化工、能源输送、医学等多个领域应用前景广阔[1~2]。
筒状立体机织物是管状织物与三维机织技术的有机结合,立体机织结构克服了层间强度低、剪切强度差、易分层等缺陷,具有结构的多样性、形态的可设计性、性能的综合性等优点。2.5D结构是筒状织物中常见的结构,其虽早已广泛应用到工程实践中,但针对2.5D结构筒状织物细观几何关系描述的文献很少。很多人认为2.5D结构筒状织物仅仅是把2.5D结构平移到圆形模具上,与普通2.5D结构织物并无差异,这种观点是不科学的。2.5D结构筒状织物具有不同于普通2.5D结构织物的几何形态,这种差异会对细观几何结构产生一定影响。
为了对织物细观结构进行更准确描述,国内外很多学者对织物截面提出过很多假设。20世纪30年代,Pierce提出了圆形截面假设[3]。后来Dickson[4]与Kemp[5]在Pierce的模型基础上做了修正,并提出跑道形截面的假设,并讨论了织物在紧密排列时的结构状态。Byun和Chou[6]采用了凸透镜截面假设,并建立了经纱压缩现象的关系式。Naik等[7]研究了织物结构的椭圆截面假设,对于筒状立体机织物纱线,还有很多不同的纱线截面假设。焦志文、周储伟等[8]假设纬纱正六边形截面,经纱为扇形截面,研究了圆管状立体机织复合材料的力学性能。陈阳[9]把跑道形纱线截面简化了为内切八边形截面,并对三维机织圆管单胞模型进行有限元分析。刘佳、周光明等[10]假设了三维机织管状复合材料经纬纱为椭圆截面,建立力学模型预测其工程弹性常数。这些纱线截面假设不断提出,使织物细观描述越来越接近织物真实情况,推动了织物建模研究的深入和织物性能研究水平的提高。
运用有限元模拟的方法对结构件性能进行评价,已成为复合材料结构设计过程中必不可少的一环。很多研究人员利用有限元分析方法对2.5D结构进行分析评价[11~13],其中最关键部分就是建立接近织物结构的实体模型,筒状结构件作为最常见的构件类型,准确进行筒状织物建模非常必要。
2 2.5D筒状立体织物
筒状立体机织物是管状复合材料的增强体,是构件承载的关键。本文中筒状织物的织物结构为2.5D结构,又称角联锁结构。2.5D结构是三维机织物组织中的一个重要分支,由接结经纱(或接结纬纱)、纬纱(或经纱)、衬经(填充经纱)和衬纬(填充纬纱)等纱线系统组成,前两个系统是构成三维机角联锁结构所必需的纱线,其他两个系统可以自由选择[14]。
2.5D结构具有穿过厚度方向的接结纱, 具有较高层间剪切强度、抗冲击损伤性、高比强度和高比模量,同时具有耐腐蚀、抗高温等优点,通过有效的组织结构设计,可以提高纤维、纱线对织物综合性能的贡献率。
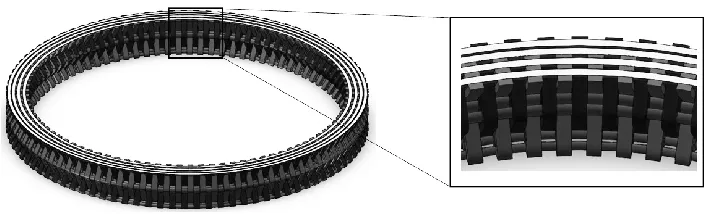
筒状立体机织物2.5D结构进行立体织造,经纱排纱图如图1所示,由排纱图可以看出2.5D结构筒状立体织物,经纱列数一定。经纱层每层的纱线数目相同,而经纱层内接圆由内而外不断增大,所以每层经纱的延展情况不同,即经纱层的厚度也不一样。
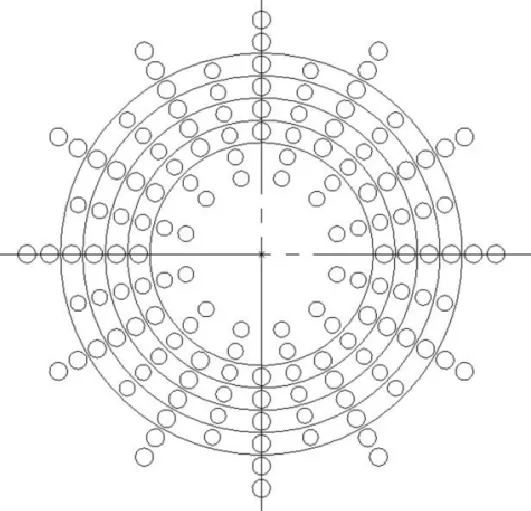
图1 经纱排纱图
3 2.5D结构筒状立体机织物细观结构
3.1 纱线截面
3.1.1 纱线截面假设
纱线截面形状的影响因素复杂,纤维的材料特性、纱线参数,织物的组织结构等都会对纱线截面产生影响。从纱线受力的角度分析,纱线的截面形状主要是受周围纱线挤压力的综合作用,而呈现不同的形状。
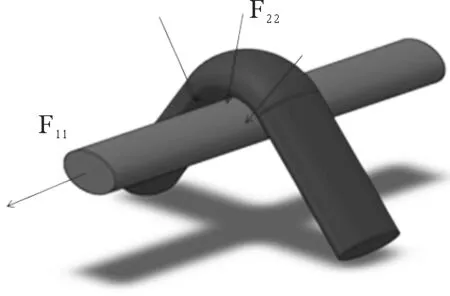
图2 经纬纱挤压作用示意图
如图2所示,F11使纱线保持顺直和集束,F22使纱线压缩变形,共同作用的结果使纱线截面呈扁平化。
如图3所示,纬纱受相邻上下经纱挤压作用两走向相反的经纱形成类双凸透镜边界。从图4纬纱显微镜照片观察到纬纱截面近似为双凸透镜,故本文将纬纱截面假设成双凸透镜形状截面,如图5。
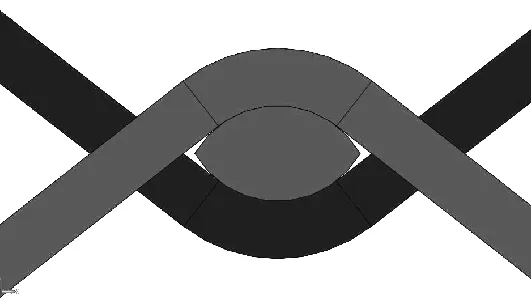
图3 经纬纱交织实体截面图
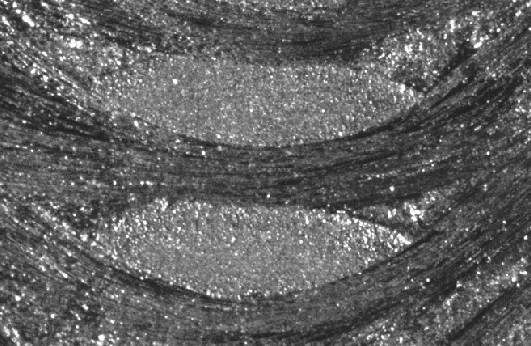
图4 纬纱截面显微镜照片
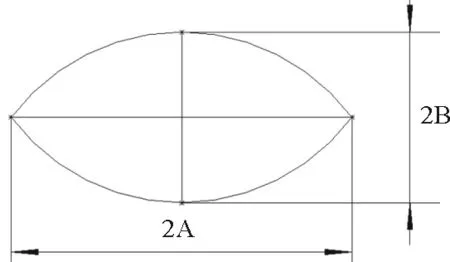
图5 纬纱截面图
经纱受上下纬纱挤压作用,又因为整个织物截面为圆形,经纱层与纬纱层相间分布,每层经纱成环形,故假设经纱截面为扇形,见图6、图7。
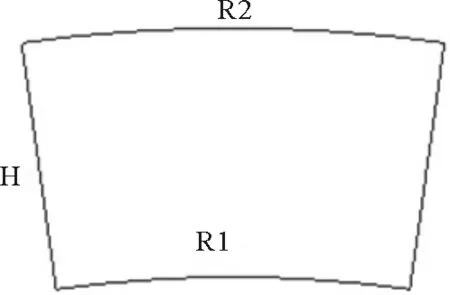
图6 经纱截面图

图7 经纬纱交织实体截面图
经纱层厚度:H=R1-R2
为了更好地建立几何模型,对于2.5D筒状立体织物的织物状态和内部结构,进行一些适当的简化假设,假设如下:
(1)织物结构均一,纬纱沿轴向排列,经纱沿圆周方向排列,经纬纱规则、紧密,纱线截面积保持不变。
(2)纬纱截面为双凸透镜形,经纱截面为扇形,相邻经纱之间无间隙,经纬纱表面相切。
(3)纬纱路径为圆形,经纱路径由直线段与弧线段组成,弧线部分与直线部分相切。
3.1.2 变截面经纱
根据对织物几何模型的假设,建立经纱和纬纱的实体模型,如图8、图9所示。经纱接结上下相邻两层纬纱(图10),由于两层经纱的厚度不同,所以经纱扇形截面是变化的(图8)。扇形截面的内径R1、外径R2及厚度H的取值已在之前讨论过,经纱路径由直线段与圆弧构成。
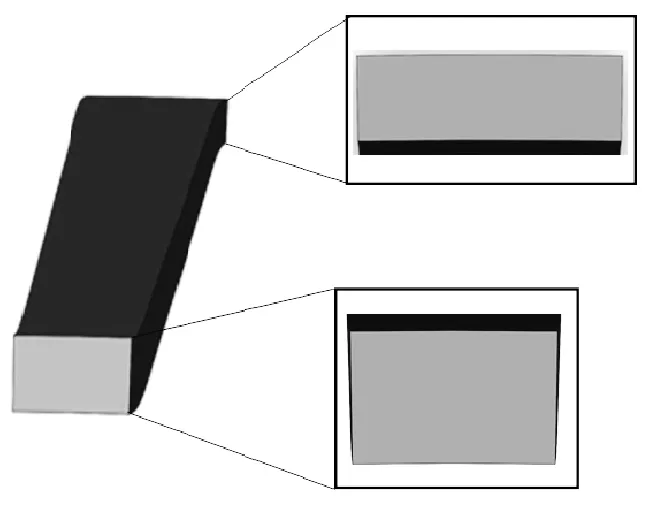
图8 变截面经纱实体模型

图9 纬纱实体模型
如图9所示,纬纱实体截面为双凸透镜形,纱线路径为圆形。经纱与纬纱实体模型按照截面参数建立,装配组成织物的实体模型,如图10所示。
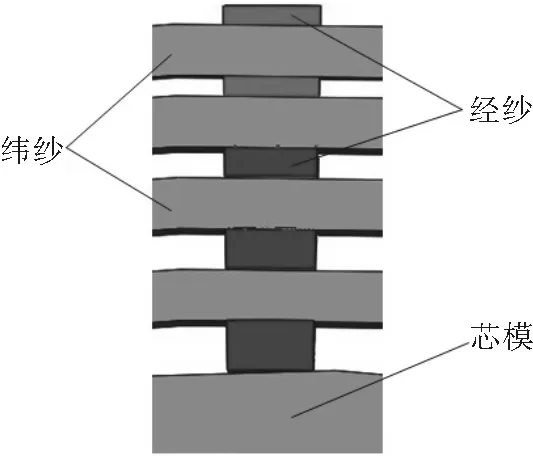
图10 筒状织物单根经纱实体模型图
3.2 织物厚度确定
由于经纱层每层经纱的延展程度不一样,经纱层厚度由内及外逐渐减小,所以经纱厚度须由芯模外径向外依次求出,才能求出最终织物厚度。求解步骤如下:
(1)已知经纱列数n,经纱截面S纱,芯模外径 R0。
(2)经纱层厚度为H=R1-R2,通过πR22=πR12+nS纱,求得R2。其中 R1为经纱层内圆,R2为经纱层外圆。第一层经纱R1内径为芯模外半径R0。
(3)下一周经纱层内圆R1′=R2+2B,其中2B为纬纱层厚度,重复步骤(2),直至最后一层经纱。
3.3 细观几何结构分析
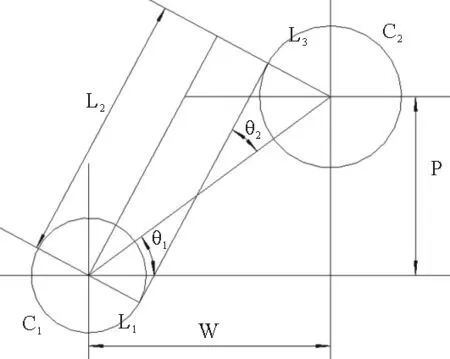
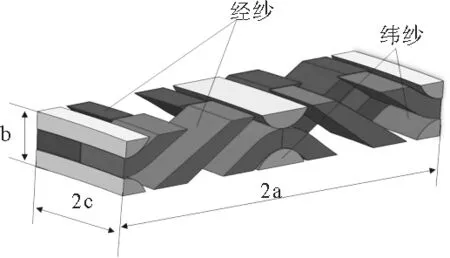
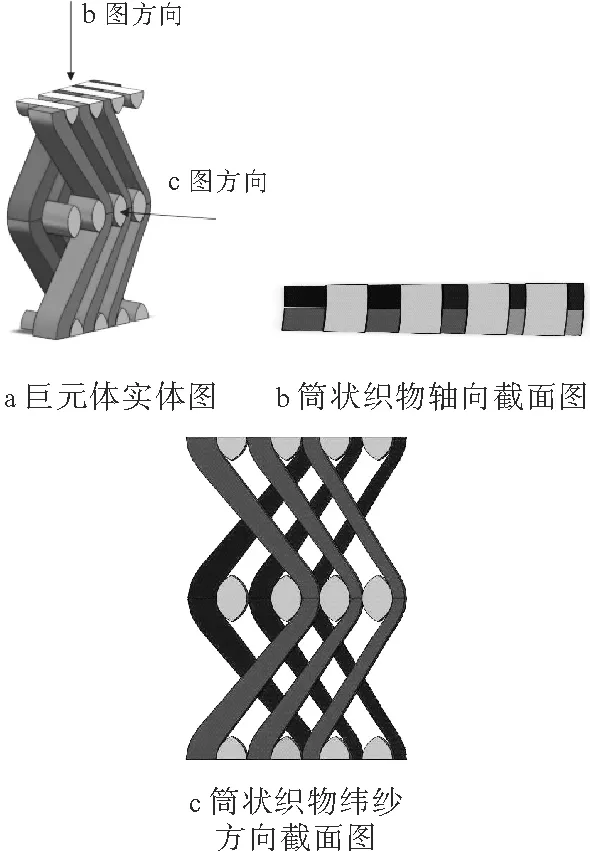
取织物的一个细观几何结构进行分析,如图11所示。H1、H2是相邻的两层经纱层厚度,经纱层厚度 H2 图11 细观几何结构示意图 双凸透镜形状由两圆相交而成,作辅助圆C1、圆C2。直线段部分倾角为θ=θ1+θ2。 图12 几何辅助求解图 由几何关系可得:两圆之间位置参数W、P的值:W=aP=b-2R+2B 直线段L1:L1=R1(θ1+θ2) 圆弧L3弧长为:L3=R2(θ1+θ2) 经纱长:L=L1+L2+L3 3.4 微元体积含量计算 如图13所示,选取长为2a,高为b,宽为2c的六面体微元,一个微元共4根经纱段,2根纬纱段。 图13 微元实体图 式中:Sj与Sw分别为经纬纱截面面积 微元内纤维体积分Vf:Vf=Vj+Vw 根据纬纱双凸透镜截面,经纱扇形变截面假设,绘制了2.5D结构筒状立体织物三维实体模型(见图14 )和2.5D结构筒状立体机织物巨元体实体图(见图15)。 图14 2.5D结构筒状立体织物实体模型图 图15 筒状织物巨元体实体图 本文基于2.5D结构筒状立体机织物显微观察和结构分析,假设双凸透镜纬纱截面以及扇形经纱截面,分析了将2.5D结构运用到筒状织物织造时所产生的细观几何差别,尤其是经纱截面形状趋于扇形截面,环形经纱层厚度由内及外不断减小的情况。分析结果表明2.5D结构筒状立体机织物不完全等同于2.5D结构立体织物,具有特殊结构特征。 为了描述细观结构,对织物结构进行了一些理想化假设。基于双凸透镜纬纱和扇形经纱,推导了2.5D的细观几何表达式和细观微元中纤维体积分数计算公式。总结了经纱层变厚度时,筒状织物厚度的求解方法,并绘制了2.5D结构筒状立体机织物三维整体模型。 虽然2.5D结构已经在实际生产中得到运用,但是对于不同形状进行近净成形时,织物结构会产生一些相应的变化,不应一律当成固定结构处理。在使用有限元方法对构件进行模拟分析时,更应关注所建织物模型的准确性,这样才能得到更准确的模拟结果。 [1] 车剑飞,黄洁雯,杨娟.复合材料及其工程应用[M].北京:机械工业出版社,2006. [2] 张晓明,刘雄亚.纤维增强热塑性复合材料及其应用[M].北京:化学工业出版社,2006. [3] Pierce F T. The Geometry of Cloth Structure[J].Journal of the Textile Institute,1937, 28(2):45—96. [4] Dickson J. Practical Loom Experience on Weavablity Limits[J].Textile Research Journal, 1954,24(12):1083—1093. [5] Kemp A. An Extension of Peirce's Cloth Geometry to the Treatment of Non-circular Threads [J].Journal of the Textile Institute,1958,49(1):44—48. [6] Byun J H,Chou T W. Elastic Properties of Three-dimensional Angle-interlock Fabric Preforms [J].Journal of the Textile Institute,1990,81(4):538—548. [7] Naik N K Kuchibhotla R.Analytical Study of Strength and Failure Behaviour of Plain Weave Fabric Composites Made of Twisted Yarns[J].Composite Part A Applied Science and Manufacturing 2002,33(5):697—708. [8] 焦志文,周储伟.圆管状立体机织复合材料的多尺度分析[J].复合材料学报,2010,(5):122—128. [9] 陈阳.圆织立体碳纤维复合材料三角架的强度分析[D].上海:东华大学,2014. [10] 刘佳,周光明,王新峰,等.三维机织管状复合材料力学模型与实验验证[J].南京航空航天大学学报,2004,36(4):444—448. [11] 姚瑶,金利民.层层接结三维角联锁机织复合材料的三点弯曲疲劳破坏[J].纤维复合材料,2014(2): 41—44. [12] 王春霞,宋孝浜,金利民.三维角联锁机织复合材料三点弯曲破坏的有限元计算[J].纺织学报,2014(3):41—45. [13] 陈凡军,罗军,陈革.三维角联锁机织复合材料有限元分析[J].东华大学学报(自然科学版),2015(1):28—31. [14] 郭兴峰.三维机织物[M].北京:中国纺织出版社,2015. 声 明:为适应我国信息化建设需要,扩大作者学术交流渠道,本刊已加入《中国学术期刊(光盘版)》、《中国万方数字化期刊群》、《中文科技数据库》、《中教数据库》和超星“域出版”平台。作者文章著作权使用费与本刊稿酬一次性给付(已在收取发表费时折减和换算为杂志赠阅)。如作者不同意将文章编入上述数据库,请在来稿时声明,本刊将做适当处理。 Meso-analysis and Modeling of Tubular Woven Fabric with 2.5D Structure ShaoMingzheng (Institute of Composite Materials of Tianjin Polytechnic University,Tianjin 300387, China) In order to explore the meso-geometry of the tubular woven fabric with 2.5D structure, lenticular cross section of weft and sector cross section of warp were assumed by means of the micrograph observation and analysis of fabric structure. The solid model of 2.5D structure tubular woven fabric and the meso-geometry model with 2.5D structure and was established. Meso geometric expression and calculation formula of fiber volume fraction in a micro-unit was also derived. The results show that when the 2.5D structure is used in the tubular fabric, some changes have occurred in the meso-geometry structure. tubular woven fabric; 2.5D structure; meso-geometry model 2016-11-10 邵明正(1989—),男,山东临沂人,硕士研究生。 TS105.1+13 A 1009-3028(2016)06-0041-05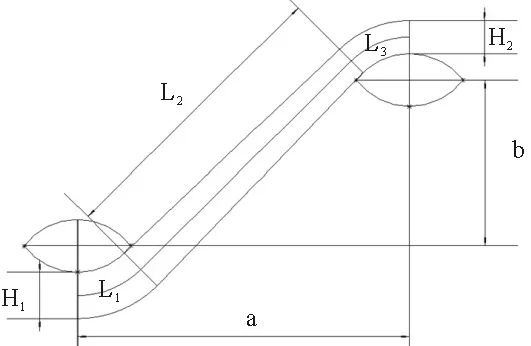
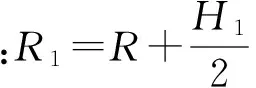
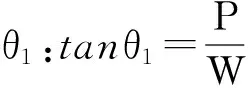
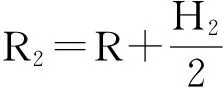
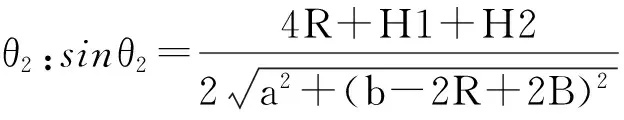
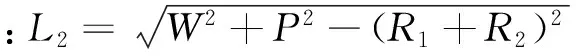
4 结语

