面向城市交通应用的移动对象聚类算法比较研究
刘 文 凯,唐 建 波,蔡 建 南,熊 强 强,刘 启 亮
(中南大学地球科学与信息物理学院地理信息系,湖南 长沙 410083)
面向城市交通应用的移动对象聚类算法比较研究
刘 文 凯,唐 建 波,蔡 建 南,熊 强 强,刘 启 亮
(中南大学地球科学与信息物理学院地理信息系,湖南 长沙 410083)
移动对象聚类方法已被广泛应用于城市交通系统中移动对象的动态聚类模式挖掘,然而,当前对于现有移动对象聚类算法在城市交通中的实际效果尚缺乏客观的分析与评价。为此,该文选取4种具有代表性的移动对象聚类算法(Swarm模式、Convoy模式、Platoon模式、Moving Cluster模式),针对北京市出租车移动数据中的拥堵现象挖掘进行实验分析与比较:1)定义模式数量、模式生存期及模式运动距离等指标定量评价和比较现有算法挖掘拥堵现象的能力;2)采用不同的对象数目阈值和时间阈值等参数阈值进行测试,分析算法阈值对移动对象聚类结果的影响。实验结果表明, 4种模式中的Convoy模式挖掘虚假拥堵现象的概率最低,挖掘拥堵现象的能力最强。4种移动对象聚类方法对阈值的设置均比较敏感,时间连续性约束对聚类结果有着显著影响。最后,对现有算法在城市交通应用中的适用性给出了相关建议。
移动对象;聚类分析;GPS轨迹
近年来,随着移动通讯技术与GPS定位技术的不断发展,已经获取了海量的移动对象位置数据,如城市车辆位置数据、飓风轨迹数据、动物迁徙数据及人类活动位置数据等[1-3]。这些移动对象位置数据库中通常包含一些彼此空间邻近且共同移动的对象集合,即移动对象聚集模式[4]。分析这类移动对象聚集模式对于研究地理现象的发展变化机理具有重要的价值,且已经广泛应用于城市交通与安全、天气预测、动物迁移分析等领域[5-9]。尤其在城市交通领域,移动对象聚集模式可以直接用于发现和预测城市系统中的拥堵现象[10],进而服务于城市路况分析、热点区域挖掘和导航线路规划[11-13]。当前,在城市交通领域,国内外学者虽然已针对移动对象聚集模式挖掘开展了初步研究,并在空间聚类算法的基础上发展了一系列移动对象聚类算法,但对这些算法的实际应用效果尚缺乏客观分析与评价。为此,本文首先对移动对象聚集模式挖掘算法进行分析和归纳,进而采用北京市出租车GPS轨迹数据对4种具有代表性的移动对象聚类算法的特点与实际应用效果进行对比和分析,以期为实际应用提供指导。
1 移动对象聚类算法
移动对象聚类旨在发现共同运动(满足空间邻近)一定时间的移动对象集合。定义一个移动对象聚集模式需要考虑两方面约束:1)对象存在约束,移动对象是否始终存在于聚集模式中;2)时间连续约束,移动对象的空间邻近性是否在每个时间点上都满足。依据这两类约束,本文将现有移动对象聚集模式分为两类(表1):对象不变模式与对象可变模式。
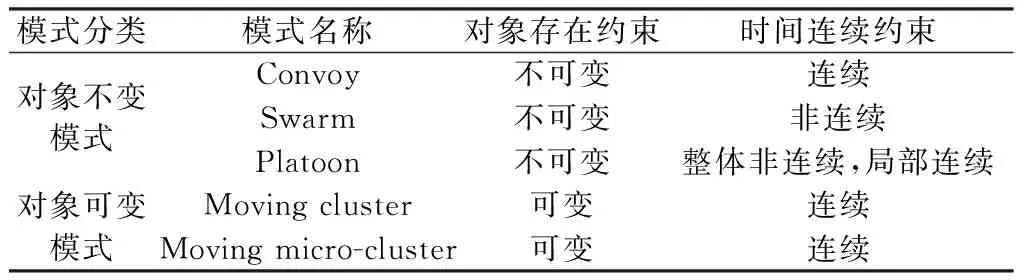
表1 现有移动对象聚类模式对比
1.1 对象不变模式聚类算法
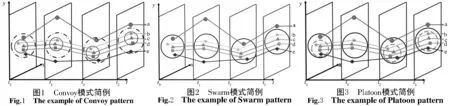
Jeung等[14]提出了移动对象聚集模式的Convoy模式。Convoy模式定义为一定数目且共同运动至少K个连续时间段的移动对象集合。挖掘Convoy模式时,首先在每个时间快照上采用空间聚类算法(如DBSCAN算法[15])分析空间聚集模式,将第一个时间快照的聚类结果作为候选Convoy模式集。进而,将下一个时间快照的空间聚类结果与候选Convoy模式集进行比对,并将共同移动对象数目大于给定阈值的聚类结果与候选Convoy模式集对应聚类结果合并,生成新的候选Convoy模式集。遍历所有时间快照之后,检索候选Convoy模式集中存在时间大于给定时间阈值的候选Convoy模式,将其视为一个Convoy模式。如图1所示,t0、t1、t2、t3为4个时间快照,在这4个时间快照中共有a、b、c、d、e 5个移动对象,每个时间快照上发现的空间聚集模式如图中虚线区域所示。在t0中,a、b、c、d、e同属于一个聚集模式;在t1中,b、c、d同属于一个聚集模式;在t2中,a、b、c、d、e同属于一个聚集模式;在t3中,b、c、d、e同属于一个聚集模式。给定移动对象数目阈值2,存在时间阈值2,则b、c、d这3个移动对象组成一个Convoy模式(实线所示)。另有学者提出的Flock模式[16]可以视为Convoy模式的一种特例,Flock模式要求每个时间切片上的空间聚集模式均包含在固定大小的圆形区域中,而Convoy模式对空间聚集模式的形状没有约束。
Li等[17]在Convoy模式的基础上,放宽对时间连续性的约束,进一步提出了Swarm模式。Swarm模式定义为一定数目且共同运动至少K个时间段的移动对象集合(K不需要连续)。Swarm模式挖掘算法首先在每个时间快照上发现空间聚集模式,然后建立对象集搜索空间,采用深度优先顺序遍历该搜索空间的每一个节点,如果节点符合Swarm的定义规则,则该节点可视为一个Swarm模式。如图2所示,在t0、t1、t2、t34个时间快照中共有a、b、c、d、e 5个移动对象,每个时间快照上发现的空间聚集模式如图中实线区域所示。在t0中,a、b、c、d、e同属于一个聚集模式;在t1中,b、c、d同属于一个聚集模式;在t2中,a、b、c、d、e同属于一个聚集模式;在t3中,b、c、d、e同属于一个聚集模式。给定移动对象数目阈值2,存在时间阈值2,则图中可发现3个Swarm模式,{(a,b,c,d,e),(t0,t2)}、{(b,c,d ),(t0,t1,t2,t3)}和{(b,c,d,e),(t0,t2,t3)}。同一个移动对象可以属于多个Swarm模式,且Swarm模式中的移动对象可在不连续的时间快照上出现在同一个聚集模式中。
Li等[18]定义了一种时间约束介于Convoy模式和Swarm模式之间的Platoon模式。Platoon模式定义为一定数目且共同运动至少K个时间段的移动对象集合,K个时间段可在全局不连续,但至少包含n个连续的局部时间段。挖掘Platoon模式时,首先在每个时间快照上采用空间聚类算法(如DBSCAN算法[15])发现空间聚集模式,进而依据空间聚类算法结果建立对象空间迭代树,通过深度优先顺序遍历该树,若树的节点能够满足Platoon模式的定义规则,那么该节点可识别为一个Platoon模式。如图3所示,在t0、t1、t2、t34个时间快照中共有a、b、c、d、e 5个移动对象,每个时间快照上发现的空间聚集模式如图中实线区域所示。在t0中,a、b、c、d、e同属于一个聚集模式;在t1中,b、c、d同属于一个聚集模式;在t2中,a、b、c、d、e同属于一个聚集模式;在t3中,b、c、d、e同属于一个聚集模式。给定移动对象数目阈值4,全局存在时间阈值3,局部存在时间阈值2,那么在图中只有一个Platoon模式,即{(b,c,d,e),(t0,t2,t3)}。可见,在该Platoon模式中,时间快照(t0,t2,t3)在整体上并不连续,但包含t2,t3这两个连续的局部时间快照。
1.2 对象可变模式聚类算法
与对象不变模式相比,在对象可变模式中,依然要求移动对象在空间上的邻近性与时间上的连续性,但允许移动对象聚类模式中的成员发生变化。对象可变移动对象集聚模式挖掘具体可采用两种策略:
(1)时空分治的策略。Kalnis等[4]从时空分治的角度发展了挖掘Moving Cluster模式的方法,其首先在每个时间快照上采用空间聚类算法(如DBSCAN算法[15])聚类发现空间聚集模式,然后计算连续时间快照中不同聚集模式的Jaccard相似性系数,如果Jaccard相似性系数超过给定阈值,那么两个相邻时间快照中不同的聚集模式便组成了一个Moving Cluster模式。如图4a所示,采用DBSCAN算法[15]在每个时间快照上发现空间聚集模式,在t0、t1、t23个时间快照上,共有C1、C2、C3 3个聚集模式(如实线圆所示),在C1中包含a、b、c、d、e 5个移动对象,在C2中包含b、c、d 3个移动对象,在C3中包含a、b、c、d、e 5个移动对象。聚集模式C1和C2的Jaccard相似性系数为0.6,C2和C3的Jaccard相似性系数为0.6,若设置的Jaccard相似性系数阈值为0.6,则在时间快照t0、t1、t2中只有一个Moving Cluster{C1,C2,C3}。国内外学者亦对Moving Cluster模式挖掘中的效率提高以及空间聚类合并等问题开展了诸多改进工作[12]。
(2)动态维护的策略。在每一个时间快照上进行聚类会耗费大量的时间[19],为解决该问题,Li 等在BIRCH算法[20]的基础上提出了Moving Micro-cluster算法:首先在初始阶段采用空间聚类方法(如K-means[21])对移动对象进行聚类,在得到的聚类结构基础上持续探测该聚集模式的最小外包矩形是否超过给定阈值,同时处理碰撞和分离事件,并进一步采用动态数据结构(KDS)[22]减少查找边界点的时间。如图4b所示,5个移动对象在不同时间快照上聚类结构的外包矩形如实线框所示,从t1时刻起,尽管空间聚类结构中的成员发生了分离(如对象a)与汇入(如对象e),但一直满足最小外包矩形阈值,因此被识别为一个移动聚类结构。Jensen等[23]进一步发现上述策略在碰撞和分离事件的探测过程中浪费大量时间,通过综合移动对象当前和未来位置定义相似性度量指标,评估移动聚集模式的分裂和合并,进而提高算法效率。

图4 对象可变模式简例
分析当前的移动对象聚类方法:1)对象不变的方法有利于对移动对象个体的移动聚集模式进行挖掘,然而Convoy模式中对时间连续性约束过于严格,可能遗漏部分移动聚集模式,但是一些放松时间连续性约束的方法(如Swarm)亦容易发现一些虚假的移动聚集模式;2)对象可变的方法虽然实际操作较为容易,但是对移动对象个体的运动模式反映不足(不同时间快照上簇内成员的变化可能较大)。
2 实验设计与分析
本文采用2012年12月1日北京市12 409辆出租车移动对象数据(图5)对上述4种代表性方法(Swarm、Platoon、Convoy和Moving Cluster挖掘算法)挖掘交通拥堵的能力进行对比分析。每个移动对象包含9种属性信息:车辆标识、触发事件、运营状态、GPS记录时间、经度、纬度、速度、方向和GPS状态。虽然出租车从绝对数量上在城市机动车保有量中所占的比例并不高,然而相较于私家车等其他车辆,同时考虑到其运营时间的持续性,其在城市道路交通中所占比例相当可观,利用出租车的运行信息间接地估计城市道路的拥堵状况是可行的[13,24,25]。
本文设置时间粒度为1 min,仅选取经纬度信息进行实验。实验中,选择拥堵高发的3个上下班时间段(即7:00-10:00,11:00-14:00,17:00-20:00)对4种方法进行测试,并从两方面对现有的移动对象聚集模式算法进行对比分析:1)挖掘出的模式数量、模式生存期及模式运动距离等差异;2)不同的阈值设置得到的聚类结果差异。

图5 出租车移动对象数据示例
上述移动对象聚类算法均需首先提取每个时间快照上的空间聚集模式,由于DBSCAN算法[15]能够有效发现不同形状的空间聚集模式,因此实验中选取该算法提取移动对象中的空间聚集模式,算法的空间半径参数(Eps)默认设置为 100 m,最小包含点参数(Minpts)设置为3。对于Swarm模式、Convoy模式以及Platoon模式,将对象数目阈值均设置为3,前两种模式的生存期阈值设为3 min,Platoon模式全局生存期阈值设置为3 min,局部生存期阈值设置为2 min。Moving Cluster 模式中Jaccard系数阈值设置为0.8。为了方便表达,本文将时间段7:00-10:00表示为时间段1,11:00-14:00表示为时间段2,17:00-20:00表示为时间段3。
2.1 聚类结果对比分析
上述4种移动对象聚类算法在3个时间段内发现的移动对象聚集模式数目如图6所示。可以发现,在任一时间段,Swarm模式数量最多,与其他3种算法发现的移动对象聚集模式数量差别较大,Platoon模式与Moving Cluster模式数量相当,Convoy模式数量最少。4种移动对象聚集模式在时间段17:00-20:00的数量最多,在11:00-14:00的数量次之,在7:00-10:00的数量最少,这与日常生活中的晚高峰较早、中高峰交通更拥堵现象相一致。
移动对象聚集模式的生存期及运动距离的对比结果如图7所示。模式生存期代表某一时间段内所有该模式生存时间的平均值,模式运动距离代表某一时间段内该模式所有对象共同运动距离的平均值。拥堵模式大致应该满足模式运动距离短且生存期长这两方面条件(表征了车辆移动缓慢的特点)。从图7可以看出:1)Swarm模式与Platoon模式均表现出模式生存期长且运动距离长的特点,可以推断二者发现虚假拥堵现象的概率较大;2)Moving Cluster模式表现出模式生存期短且运动距离短的特点,这可能是由于该模式对于时间连续性没有约束,导致发现了较多无意义的小簇;3)Convoy模式最为符合交通拥堵模式运动距离短且生存期长的特点,可以推断其发现真正交通拥堵的能力较强。

2.2 聚类参数影响分析
为探究不同的阈值设置对移动对象聚类算法结果的影响,以时间段3为例进行实验分析。为了测试单个阈值的设置对聚类结果的影响,实验时每次仅改变一个测试阈值,而保证其他阈值为默认值。首先对Swarm模式、Platoon模式和Convoy模式挖掘中的两个关键阈值(对象数目阈值和时间阈值)进行分析,实验结果如图8所示。可以发现,随着对象数目阈值的增大,移动对象聚类模式的数量随之迅速减少,但在对象数目阈值超过6后,聚类模式数目变化不大;随着时间阈值的增大,Swarm模式和Platoon模式的数量迅速减少,但时间阈值对Convoy模式的影响最小。
进而,对影响Moving Cluster模式挖掘的关键阈值(DBSCAN算法的最小包含点数(Minpts)与Jaccard相似性系数阈值)进行分析,实验结果如图9所示。可以发现,随着Minpts增大,得到的Moving Cluster模式数目随之减少,当Minpts从3增大到5时,Moving Cluster模式的数目减少速度最快;随着Jaccard相似系数阈值的增大,发现Moving Cluster模式的数目随之减少, Jaccard相似系数阈值超过0.7后,Moving Cluster模式的数目变化不大。上述参数变化规律亦可以为实际应用中阈值设置提供一定的参考。
2.3 实验结果分析与讨论
依据上述实验结果,对文中4种方法的性能与适用性进行分析和总结:1)Swarm模式数目最多的主要原因在于其对时间连续性的约束过于宽松,导致发现的模式中包含较多的非拥堵现象,亦是Swarm模式运动距离与生存期长的主要原因;伴随着时间连续性约束越来越严格(Platoon和Convoy模式),模式的数量、运动距离、生存期均减少。可见,模式的时间连续性约束对移动对象聚集模式挖掘的影响最为显著。2)对于Moving cluster模式,虽然其对移动对象在聚类模式中的时间阈值没有约束,但是其限定了相邻两个时间切片间连续性的约束与相邻时间切片间的相似性约束,Moving Cluster的数量仅比Convoy模式稍多。由于Moving Cluster的时间连续约束比Convoy模式更宽松,发现了更多细碎的移动模式,故该模式的运动距离与生存期比Convoy模式更短。3)由于Convoy模式对移动对象聚集模式定义的约束最为严格,其对参数阈值的敏感性相对较低,而其他几种算法均对阈值较为敏感。Convoy模式最为符合拥堵模式生存期长且运动距离短的特点,在实际中发现真正交通拥堵的能力较强。但是,在实际中如何依据应用需求与应用目的选择聚类参数依然是一个必须要重视的问题。4)上述4种算法发现交通拥堵时,仅考虑了时间切片上的聚集性与时间的连续性,而没有顾及车辆的运行距离与运行速度,这也是发现虚假移动对象聚集模式的一个重要原因,如图10所示,上述移动对象虽然一起运动了一定时间,但是相邻时间的模式运动距离较长,并没有产生相邻时间切片上空间邻近性的聚集现象。此外,当前算法大多仅在欧式空间研究移动对象的聚集模式,而忽视了路网对移动对象的约束,因此需要进一步研究路网约束对移动对象聚集模式挖掘的影响[26,27]。
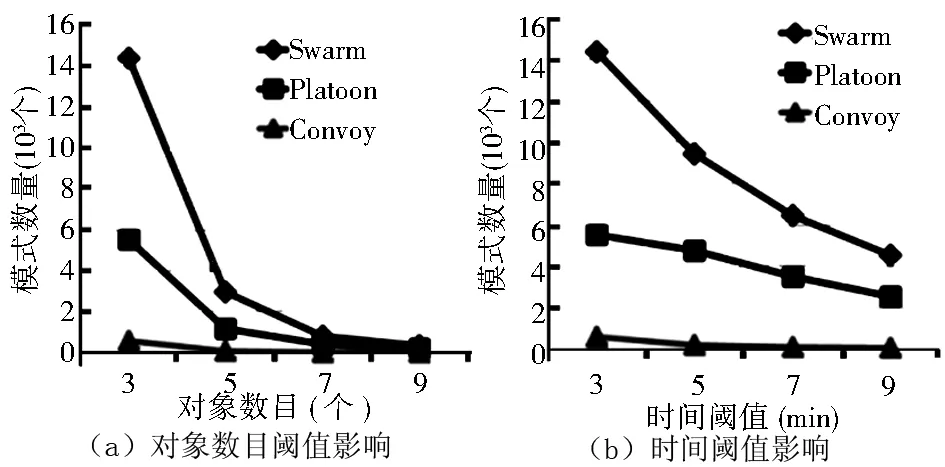
图8 不同参数对Convoy,Swarm和Platoon模式挖掘影响
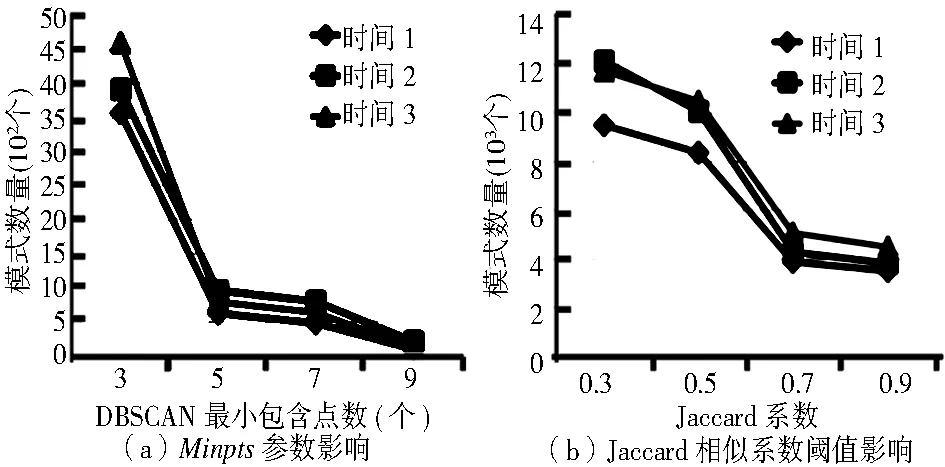
图9 不同参数对Moving Cluster挖掘结果影响

图10 现有移动对象聚类算法发现的非拥堵模式
3 结论与讨论
本文对现有4种代表性的移动对象聚集模式挖掘算法在城市交通中的应用效果进行了对比研究,并采用北京市出租车移动数据,从模式数量、模式生存期及模式运动距离等方面对现有方法发现移动对象交通拥堵的实际效果进行了实验分析,同时对比了不同阈值对聚类结果的影响。结果发现:1)时间连续性约束对于移动对象聚集模式挖掘具有显著影响,直接影响模式数量、模式生存期及模式运动距离;2)虽然现有算法均有发现虚假拥堵的问题,但对于时间连续性约束较严格的方法(如Convoy和Moving Cluster)而言,发现虚假拥堵的概率相对较低;3)现有方法对参数阈值较为敏感,尚缺乏较为通用、客观的阈值设置方法。
本研究尚存在两方面的不足:1)没有对算法的效率进行分析,在分析交通大数据时,算法的效率亦是必须考虑的问题;2)仅采用出租车移动对象数据进行分析,而不同类型的移动对象聚集模式的特征与性质可能存在差异,亦有算法的偏向性。进一步的研究工作将侧重于以下两方面:1)移动对象全生命周期聚集模式挖掘,如区分城市交通拥堵中的4个过程(开始、发展、拥堵、衰退),如何发现这一过程对于城市交通规划具有重要意义;2)路网约束下的移动对象聚集模式挖掘模型构建。
[1] 李婷,裴韬,袁烨城,等.人类活动轨迹的分类、模式和应用研究综述[J].地理科学进展,2014,33(7):938-948.
[2] 谭祥爽,王静,宋现锋,等.基于浮动车数据的路口探测方法[J].地理与地理信息科学,2015,31(5):34-38.
[3] 杨伟,艾廷华.基于众源轨迹数据的道路中心线提取[J].地理与地理信息科学,2016,32(3):1-7.
[4] KALNIS P,MAMOULIS N,BAKIRAS S.On discovering moving clusters in spatio-temporal data[A].Proceedings of the 9th International Conference on Advances in Spatial and Temporal Databases[C].Berlin,Germany,2005.364-381.
[5] PEI T,WANG W,ZHANG H,et al.Density-based clustering for data containing two types of points[J].International Journal of Geographical Information Science,2015,29(2):1-19.
[6] ROSSWOG J,GHOSE K.Detecting and tracking coordinated groups in dense,systematically moving,crowds[A].SIAM International Conference on Data Mining[C].2012.
[7] WANG Y,LUO Z,TAKEKAWA J,et al.A new method for discovering behavior patterns among animal movements[J].International Journal of Geographical Information Science,2015,30(5):929-947.
[8] LI Z H,HAN J W,JI M,et al.MoveMine:Mining moving object data for discovery of animal movement patterns[J].ACM Transactions on Intelligent Systems & Technology,2011,2(4):135-136.
[9] TRIPATHI P K,DEBNATH M,ELMASRI R.Extracting dense regions from hurricane trajectory data[A].The Workshop on Managing & Mining Enriched Geo-Spatial Data[C].New York,USA,2014.1-6.
[10] 鲁小丫,宋志豪,徐柱,等.利用实时路况数据聚类方法检测城市交通拥堵点[J].地球信息科学学报,2012,14(6):775-780.
[11] KUIJPERS B,OTHMAN W.Modeling uncertainty of moving objects on road networks via space-time prisms[J].International Journal of Geographical Information Science,2009,23(9):1095-1117.
[12] 张峻铭,李静林,王尚广,等.基于时空图的移动对象聚集模式挖掘方法[J].软件学报,2016,27(2):348-362.
[13] LIU S,LIU Y,NI L M,et al.Towards mobility-based clustering[A].Proceedings of the 16th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining[C].New York,USA,2010.919-928.
[14] JEUNG H,YIU M L,ZHOU X,et al.Discovery of Convoys in trajectory databases[J].Computer Science,2010,1(1):1068-1080.
[15] ESTER M,KRIEGEL H P,SANDER J,et al.A density-based algorithm for discovering clusters in large spatial databases with noise[A].Proceedings of KDD-96(C)[C].1996,96(34):226-231.
[16] LAUBE P,IMFELD S.Analyzing relative motion within groups of trackable moving point objects[A].International Conference on Geographic Information Science[C].Berlin Germany,2002.132-144.
[17] LI Z,DING B,HAN J,et al.Swarm:Mining relaxed temporal moving object clusters[A].Proceedings of the Vldb Endowment[C].2010,3(1):723-734.
[18] LI Y,BAILEY J,KULIK L.Efficient mining of platoon patterns in trajectory databases[J].Data and Knowledge Engineering,2015,100:167-187.
[19] LI Y,HAN J,YANG J.Clustering moving objects[A].Proceedings of the Tenth ACM SIGKDD International Conference on Knowledge Discovery and Data Mining[C].New York,USA,2004.617-622.
[20] ZHANG T,RAMAKRISHNAN R,LIVNY M.BIRCH:An efficient data clustering method for very large databases[A].Proceedings of the 1996 ACM SIGMOD International Conference on Management of Data[C].New York,USA,1996.103-114.
[21] MACQUEEN J.Some methods for classification and analysis of multivariate observations[A].Proceedings of the 5th Berkeley Symposium on Mathematical Statistics and Probability[C].1967.281-297.
[22] BASCH J,GUIBAS L J,HERSHBERGER J.Data structures for mobile data[J].Journal of Algorithms,1999,31(1):1-28.
[23] JENSEN C S,LIN D,OOI B C.Continuous clustering of moving objects[J].IEEE Transactions on Knowledge and Data Engineering,2007,19(9):1161-1174.
[24] 张俊涛,李志勇,张浩,等.利用出租车轨迹数据估计城市道路拥堵状况[J].测绘工程,2016,25(9):68-72.
[25] 赵天天,张晶,王彦兵.基于实时路况数据的原发性交通拥堵点判别——以北京市二环以内为例[J].地理与地理信息科学,2015,31(3):104-107.
[26] CHEN J,MENG X.Clustering analysis of moving objects[A].Moving Objects Management[C].Berlin,Germany,2010.151-171.
[27] 翟丹润,马骏.基于道路网络的移动对象的聚类算法研究[J].河南大学学报(自然科学版),2011,41(1):95-97.
Algorithm Comparison for Clustering of Moving Objects in Traffic System
LIU Wen-kai,TANG Jian-bo,CAI Jian-nan,XIONG Qiang-qiang,LIU Qi-liang
(DepartmentofGeo-informatics,SchoolofGeosciencesandInfo-physics,CentralSouthUniversity,Changsha410083,China)
Existing location-acquisition technologies such as Global Positioning Systems and Wireless Sensor Networks have generated large amounts of moving object data.Discovery of clustering patterns from moving objects is useful for the study of wildlife migration,the prediction of travel time and the prediction of anomalies in traffic systems.Currently,clustering of moving objects has played a key role in spatio-temporal data mining,and a series of moving objects clustering algorithms have been proposed based on the spatial clustering algorithms.Although the application of moving objects clustering in traffic systems has attracted more attentions in recent years,an objective evaluation of existing moving objects clustering algorithms is still lacking.On that account,a comparative analysis of four typical moving objects clustering algorithms (Convoy,Swarm,Platoon and Moving Cluster) is presented in this study.The GPS (Global Position System) trajectories dataset in Beijing is used to test the performance of different algorithms.The performance of these algorithms is evaluated based on the number of patterns,the lifetime of patterns and the moving distances of patterns.The experimental results show that the clustering results are seriously affected by the time continuous constraint,and the method designed for discovering Convoy pattern is the most effective for the discovery of traffic congest.The effect of clustering parameters on these four algorithms is also analyzed.
moving objects;clustering analysis;GPS trajectories
2016-09-16;
2016-10-24
国家自然科学基金项目(41601410);资源与环境信息系统国家重点实验室开放基金;国家级大学生自由探索项目(201610533401)
刘文凯(1993-),男,硕士研究生,主要研究方向为时空动态目标聚类分析。E-mail:wenkai.liu@csu.edu.cn
10.3969/j.issn.1672-0504.2016.06.012
TP311.13;U491.1
A
1672-0504(2016)06-0069-06

