三角代数的三重导子

谢乐平

（怀化学院数学与计算科学学院，湖南怀化418008）

三角代数的三重导子

谢乐平

（怀化学院数学与计算科学学院，湖南怀化418008）

设A，B是有单位元的交换环R上的代数，M为（A，B）-双模，Δ为三角代数.构造了三个自然线性映射，结合模论的方法，得到三角代数Δ的三重导子能表示为三个标准三重导子之和.

三角代数；三重导子

假定A，B是环R上的代数，M是一个（A，B）-双模，三角代数（有时称为形式三角矩阵代数）指具有通常的矩阵运算的如下代数

人们对这种三角代数（环）进行了许多研究.如文献[1]系统地研究了各种环论性质（如左kasch模，右极小内射环，clear环，环，右PF环等）的形式三角矩阵环.文献[2]研究了三角代数的交换映射，即使[L（a），a]的线性映射L，这里a是三角代数的任一元素.文献[3]证明了三角代数的每个Lie导子都能表示成一个导子与一个映到其中心的映射之和.文献[4]研究了三角代数上双可加映射（B（x，x）x=xB（x，x）），作为应用由此确定了三角代数上的交换保持映射和Lie自同构.文献[5]得出了三角代数的Jordan同构或者是同构，或者是反同构.文献[6]证明了三角代数的Jordan导子都是导子等等.

关于各种（Lie）代数上的导子，Lie导子，Jordan导子等已有很多研究结果，如文献[3，6-9]等（未全列出）.近年来，有些学者将导子的概念进行了推广，提出了双导子的定义，如文献[10]证明了非交换素环上的双导子都是内双导子.文献[11]给出了双导子在某些域上的应用，文献[7，12，13]等都是研究双导子的.更进一步，文献[14-17]把导子的概念推广到了三重，参阅这些文献可以看出研究三重导子是有意义的工作，所以我们研究三角代数上的三重导子.

假定R是有单位元的交换环，A，B是环R上有单位元的代数，M为环R上的（A，B）-双模，也就是M既是左A-模，又是右B-模，且∀a∈A，m∈M，b∈B，有（am）b=a（mb）.为了简便并且不会混淆，我们用1表示所有环和代数的单位元.φ称为Δ上的三重导子，是指对任意X，Y，Z∈Δ，R-线性映射φ∶Δ→Δ满足

构造三重导子φ对应的三个R-自然线性映射：

那么有

先给出Δ的三重导子的一些结果.

引理1如果φ为三角代数Δ的三重导子，则φ3（I）=eφ（I）f=0.

证因为efI=0，又φ为三重导子，根据三重导子定义有

再结合式（1，2）化得

引理2如果φ为三角代数Δ的三重导子，则φ（I）≡0（modCΔ）.

因为是在交换环R上讨论，所以结合式（6），（7）得只有如下两种情况：

情况1φ1（e）g=gφ2（f）=0.

情况22φ1（e）g=2gφ2（f）=0（即φ1（e）g=gφ2（f）且特征为2）.

不难看出，情况1实际上是情况2的特殊情形.为了具体刻画三角代数Δ上的三重导子，先给出三个标准的定义：

定义2如果R-线性映射ψ∶Δ→Δ满足∀X∈Δ，ψ（X）=eXeg1+g2fXf，其中g1，g2∈ΔM并且g1+g2=0，则称ψ为三角代数Δ上的中心三重导子.

根据引理3，φ3是φ限制在M上的作用，所以如果忽略作用范围可以理解为φ=φ3，类似的给出下面的定义3.

定义3如果R-线性映射τ∶Δ→Δ满足eτf=τ，同时τ还是一个三重导子，并且∀a∈A，m∈M，b∈B有τ（amb）=aτ（m）b（即τ是双模同态），那么称τ为模三重导子.

由上述定义，可得以下性质1，2.

性质1当R的特征为2时，κ为三重导子.

即κ为三重导子.

性质2ψ∶Δ→Δ为定义2中的线性映射，则ψ为三重导子.

证任取X，Y，Z∈Δ，一方面ψ（XYZ）=e（XYZ）eg1+g2f（XYZ）f.另一方面，ψ（X）YZ=（eXeg1+g2fXf）YZ=eXeg1fYZf+g2fXYZf.类似可得

又因为g1+g2=0，所以

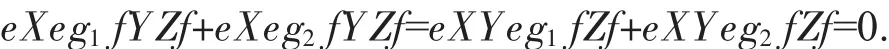
因此有ψ（X）YZ+Xψ（Y）Z+XYψ（Z）=eXYZeg1+g2fXYZf=ψ（XYZ）.

以下定理是本文的主要结论.

定理设A，B是有单位元的交换环R上的代数，M是（A，B）-双模，Δ为三角代数，φ是Δ上的三重导子，则存在倍乘映射κr∶Δ→Δ，中心三重导子ψ∶Δ→Δ，以及模三重导子τ∶Δ→Δ，使得φ=κr+ψ+τ.

证因为情况1是情况2的特殊情形，所以假设满足情况2.

根据式（6）有φ1（e）m=mφ2（f）.取r1=φ1（e），r2=φ2（f），结合式（1，2）有

同样可得f（φ-κ）（X）f=0.结合式（1，2）和引理3得

取g1=eφ（e）f，g2=eφ（f）f，根据式（4）有g1+g2=0，接下来我们引入一个中心三重导子ψ满足ψ（X）=eXeeφ（e）f+eφ（f）ffXf=eφ1（X）f+eφ2（X）f.

计算（φ-κ）（X）-ψ（X）=（φ-κ-ψ）（X）=eφ3（X）f-eκ（X）f.由性质1，2有κ，ψ均是三重导子，所以τ=φ-κ-ψ也是Δ上的三重导子.下面来说明τ还是双模同态（注意：因为τ实际可视为τ∶Δ→M，所以下面有时候就用τ表示eτf）.

也就是说，τ是双模同态.

如果满足情况1.则在上述证明过程中取r=0.完全类似可得

还可得φ-κ-ψ也是模三重导子.

[1]A.haghany，K.Varajan.Studyofformal triangular matrixrings[J].Comm.Algebra，1999，27（11）：5507-5525.

[2]W.S.Cheung.Commutingmaps oftriangular algebras[J].J.London.Math.Soc，2001，63（2）：117-127.

[3]W.S.Cheung.Lie derivations oftriangular oftriangular algebras[J].Linear Multilinear Algebra，2003，51：299-310.

[4]D.Benkovic，D.Eremita.Commutingtraces and commutativetypreservingmaps on triangular algebras[J].J.Algebra，2004，280：797-824.

[5]T.L.Wong.Jordan isomorphisms oftriangular rings[J].Proc.Amer.Math.Soc，2005，133：3381-3388.

[6]J.H.Zhang，W.Y-yua.Jordan derivations oftriangular algebras[J].Linear Algebra Appl，2006，419：251-255.

[7]D.Benkovic.Bidervations oftriangular algebras[J].Linear Algebra Appl，2009，431（9）：1587-1602.

[8]CoelhoS.P.Derivation ofupper matrixrings[J].Linear Algebra Appl，1993，187：263-267.

[9]Jondrup S.Automorphisms and derivations ofupper triangular matrixring[J].Linear Algebra Appl，1995，221：205-218.

[10]M.Brešar，W.S.Martindale，C.R.Miers，et al.Centralizingmaps in prime rings with involution[J].J.Algebra，1993，161：342-357.

[11]M.Brešar.Commutingmaps：Asurvey[J].Taiwanese J.Math，2004，8：361-397.

[12]J.H.Zhang，S.Feng，H.X.Li，R.H.Wu.Generalized biderivations ofnest algebras[J].Linear Algebra Appl，2006，418：225-233.

[13]M.Brešar.On generalized biderivations and related maps[J].J.Algebra，1995，172（3）：764-786.

[14]C.R.Miers.Lie triple derivations ofV-Nalgebras[J].Amer.Math.Soc，1978，71：57-61.

[15]Ji Peisheng，WangLin.Lie triple derivations ofTUHF algebra[J].Linear Algebra Appl，2005，403：399-408.

[16]J.H.Zhang，B.W.Wu，H.X.Cao.Lie triple derivations ofnest algebra[J].Linear Algebra Appl，2006，416：559-567.

[17]H.T.Wang，Q.G.Li.Lie triple derivations ofLie algebra ofstrictlyupper triangular matrixover a commutative ring[J].Linear Algebra Appl，2009，430：66-77.

Triple Derivations of Triangular Algebra

XIE Le-ping
（College of Mathematics and Computational Science，Huaihua University，Huaihua，Hunan 418008）

Let A，B be algebras over commutative unital ring R，M be an（A，B）bimodule.We give an explicit description of any triple derivations of the triangular algebra Δ.

triangular matrix ring；triple derivation

O151.21

A

1671－9743（2016）11－0014－04

2016-06-14

谢乐平，1976年生，男，湖南宁乡人，讲师，研究方向：代数.