单位球Dirichlet空间上的紧Toeplitz算子*

陈建军，王晓峰

(1. 肇庆学院数学与统计学院, 广东 肇庆 526061;2. 中山大学数学学院, 广东 广州 510275;3. 广州大学数学与信息科学学院,数学与交叉科学广东普通高校重点实验室,广东 广州 510006)

单位球Dirichlet空间上的紧Toeplitz算子*

陈建军1,2，王晓峰3

(1. 肇庆学院数学与统计学院, 广东 肇庆 526061;2. 中山大学数学学院, 广东 广州 510275;3. 广州大学数学与信息科学学院,数学与交叉科学广东普通高校重点实验室,广东 广州 510006)

研究单位球上Dirichlet空间上的Toeplitz算子的紧性，得到结论：有限个具有有界符号的Toeplitz算子乘积的有限和是一个紧算子，等价于它的Berezin型变换消失于单位球面。

Toeplitz算子;Berezin型变换;Dirichlet空间; 单位球

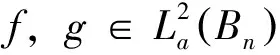
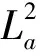
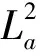
Sobolev空间L2,1(Bn)是一个由满足如下性质的复值函数所组成的函数空间，

显然，L2,1(Bn) 是一个Hilbert空间，它的内积定义为：

Dirichlet空间D2(Bn)是L2,1(Bn)的一个子空间，它由L2,1(Bn)中所有无常数项的全纯函数所组成的。D2(Bn)的内积继承于L2,1(Bn)的内积，具体为：

通过简单的计算，Dirichlet空间D2(Bn)中的再生核为：

然而，关于Dirichlet空间的研究，也有一定的成果。比如卢玉峰等[3]研究了测度符号的Toeplitz算子，并得出了它的有界性和紧性条件。在单位球的情形里，比如有：曹广福[4]研究了具有连续符号的Toeplitz算子；曹广福等[5]进一步研究具有有界符号的Toeplitz算子。

利用文献[6]的思想方法，将其中关于Toeplitz算子的结果推广到单位球区域上。由于单位球比单位圆盘拓扑结构复杂，Bergman空间和Dirichlet空间再生核的某些性质在单位球面附近只有等价关系而不是相等关系，不过还是得到相类似的结论。具体地说，本文主要研究单位球上Dirichlet空间上的Toeplitz算子的紧性。得到结论：有限个具有有界符号的Toeplitz算子乘积的有限和是一个紧算子，等价于它的Berezin型变换消失于单位球面。

与Toeplitz算子相关的其它算子，如Wiener-Hopf算子和复合算子，请参考文献[7-8]。

1 预备知识

为了证明主要定理，先给出一些预备知识。

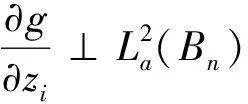
证明 参考文献[4]。

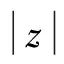
引理2 对于任意的z,w∈Bn〈{0}，有

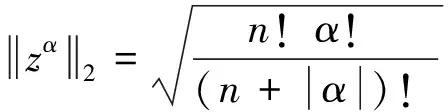
根据引理2，我们记

为一种辅助核。它有如下的性质：

引理3 对于任意给定的z,w∈Bn〈{0}，有

以及

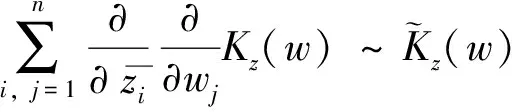
证明 由引理1，

进一步结合引理2，得到

因此，

证毕。

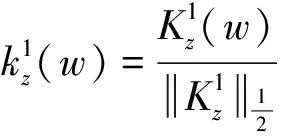
引理4 对任意非零元z,w∈Bn，

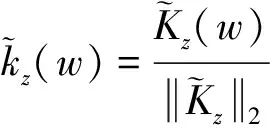
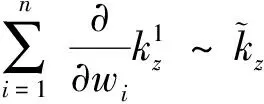
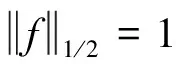
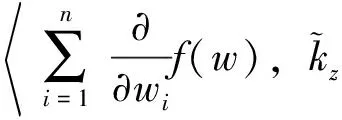
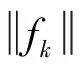
证明 参考文献[3]中的定理5。证毕。

记L∞(Bn)为单位球上本性函数空间。定义

其中i=1,2,…,n,其上的范数定义为：

定义1 取u∈L∞,1(Bn)，Dirichlet空间上Toeplitz算子Tu定义为：

其中f∈D2。

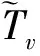
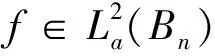
引理6 给定u∈L∞,1(Bn)，则Toeplitz算子Tu是一个有界算子。

证明 由Toeplitz算子的定义以及Kz(w)的性质，可得：对于任意的f，g∈D2，

因此，存在一个常数C，使得

这表明Tu是一个有界算子。证毕。

2 主要定理

取ui,j∈L∞,1(i,j=1,2,…,n)，定义

定理1 下列3个结论是等价的：

(i)S是一个紧算子；

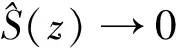
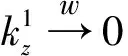
(ii)⟹(iii):结合Berezin型变换的定义和Hölder不等式，有

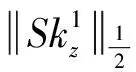
(iii)⟹(i): 不失一般性，只需证明S=∑Tu1Tu2这一情形即可。为了方便表述，算子中的小指标往往省略。

由于结论(iii)是成立的，所以当z→∂Bn时，我们有

结合上面的引理，对上式进一步地计算，得到

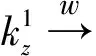
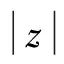
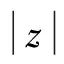
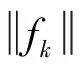
继续接着计算

同理，当k→∞时，

之前，我们已经知道Toeplitz算子S(∑∏ Tui,j)是一个紧算子，因此，由文献[9-10],

总的来说，已经证得

即S是一个紧算子。证毕。

[1] 黄昭波.Bergman空间上的Hankel算子和Toeplitz算子[J]. 复旦学报(自然科学版), 1991, 30(2): 151-157.

[2] 李颂孝, 胡俊云. 单位球上Bergman空间上的紧算子[J]. 数学学报, 2004, 47(5): 837-844.

[3]LUYF,SUNSH.ToeplitzOperatorsonDirichletSpaces[J].ActaMathSinica, 2001, 17(4): 643-648.

[4] 曹广福.Dirichlet空间上的Toeplitz算子[J]. 数学年刊, 2000, 21(4): 499-512.

[5] 曹广福, 朱渌涛.Dirichlet空间上Toeplitz算子的紧性[J]. 数学学报, 2001, 44(2): 241-248.

[6] 夏锦, 王晓峰, 曹广福.Dirichlet空间上的紧算子[J]. 数学物理学报, 2009, 29(5): 1196-1205.

[8] 何忠华, 曹广福, 何莉.Bloch-Orlicz型空间上积分型算子与复合算子的乘积[J]. 中山大学学报(自然科学版), 2016,55(1): 44-47.

[9]ENGLISM.CompactToeplitzoperatorsviatheBerezintransformonboundedsymmetricdomains[J].IntegrEquOperTheory, 1999, 33: 426-455.

[10]ENGLISM.ErratumtocompactToeplitzoperatorsviatheBerezinTransformonboundedsymmetricdomains[J].IntegrEquOperTheory, 1999, 34: 500-501.

Compact Toeplitz operators on the Dirichlet space over unit ball

CHENJianjun1,2，WANGXiaofeng3

(1. School of Mathematics and Statistics, Zhaoqing University, Zhaoqing 526061, China;2. School of Mathematics, Sun Yat-sen University, Guangzhou 510275, China;3. School of Mathematics and Information Science and Key Laboratory of Mathematics and Interdisciplinary Sciences of the Guangdong Higher Education Institute,Guangzhou University, Guangzhou 510006, China)

The compactness of Toeplitz operators on Dirichlet space is studied. It is proved that finite sums of finite products of Toeplitz operators with bounded symbols are compact if and only if their Berezin-type transforms vanish on the boundary of the unit ball.

Toeplitz operator; Berezin type transform; Dirichlet space; unit ball

10.13471/j.cnki.acta.snus.2016.06.011

2015-12-08

广州市教育局科技计划资助项目(2012A018)； 国家自然科学基金资助项目(11471084，11301101)

陈建军(1986年生)，男；研究方向：泛函分析；通讯作者：王晓峰;E-mail:wangxiaofeng514@hotmail.com

O

A

0529-6579(2016)06-0074-05