高密度聚乙烯单轴拉伸力学性能试验研究*

陈自鹏，石少卿，罗伟铭

(1. 后勤工程学院军事土木工程系，重庆 401311;2. 重庆市地质灾害防治工程技术研究中心，重庆 401311)

高密度聚乙烯单轴拉伸力学性能试验研究*

陈自鹏1,2，石少卿1,2，罗伟铭1

(1. 后勤工程学院军事土木工程系，重庆 401311;2. 重庆市地质灾害防治工程技术研究中心，重庆 401311)

随着高密度聚乙烯(HDPE)被广泛应用于化工，建筑，军工等各个领域，高密度聚乙烯的型号，使用环境也越来越多样化。因此，对在不同拉伸速率和拉伸方向下的光面HDPE片材和花纹面HDPE片材进行单轴条带拉伸试验。试验表明：光面横向受拉片材随着拉伸速率的提升，其屈服平台强度也随着提升，在拉伸速率为150mm/min时，光面横向受拉片材的第二屈服点不明显，材料抗拉性能较好。花纹面片材的最大拉伸强度的率相关性较好，在已有的3组拉伸速率下平均增长5.02%，但花纹面所受最大荷载较光面片材小。花纹面片材较光面片材更易断裂，纵向受拉片材较横向受拉片材更易断裂。结果表明，光面横向受拉片材的抗拉性能较好。

条带拉伸试验；率相关性；方向相关性；高密度聚乙烯

高密度聚乙烯作为一种可塑性强，造价低廉和耐腐蚀性能较好的热塑性树脂，被广泛运用于化工，建筑，军工等各个领域，同时国内外各个学者也对该材料的力学性能展开大量研究。G’sell和Jonas[1]最早对高密度聚乙烯(HDPE)片材进行单轴拉伸试验，并对HDPE片材后期的应力强化现象进行分析。而后，Caucher-Miri等人对HDPE在单轴拉伸下的微观力学性能进行研究。Know[2]通过试验和数值模拟引入一个修正系数，对单轴拉伸试验及其数值模拟而言，这个修正系数可以减小以往数值模拟中等效应力与实际轴力之间的误差。Zhang[3]对HDPE波纹管进行了缺口断裂拉伸试验和数值模拟研究，通过两组数学表达式分别演算HDPE的大变形和损伤发展，提供了最大伸长断裂与损伤演化率之间关系的定性描述。通过HDPE的条带拉伸试验，李俊伟[4]对HDPE片材在低拉伸速率下的拉伸应变率特性进行研究，试验表明HDPE片材的最大拉伸应力具有较明显的率相关性。

目前，随着HDPE这种优异材料的推广，国内出现了不同样式的HDPE片材，其中最为常见的是光面片材和花纹面片材，但针对不同表面的HDPE片材性能研究较少。同时，随着HDPE片材的使用范围增大，其使用环境也变得较为复杂，HDPE片材不仅仅可能受到低速率荷载作用，也可能受到较高加载速率的冲击，然而针对HDPE在较高拉伸速率下的力学性能研究也较少。

此外，在生产使用中，由于工艺手段的不同或者结构在使用一段时间后，HDPE材料会受到一个方向的拉伸力，其力学性能往往表现为具有一定的方向相关性。但是，由于HDPE作为一种热塑型高分子聚合物，其分子排列较为平均，故在以往研究中常常认为HDPE片材为各向同性材料，对于实际使用中HDPE片材力学性能的方向相关性研究较少。

因此，本文通过条带拉伸试验，对不同样式的HDPE片材在不同拉伸速率和受拉方向下的力学性能进行研究，将不同表面，拉伸方向，拉伸速率3组工况进行两两正交对比，研究HDPE片材的应力应变特性，后期通过静力和动力拉伸试验拟合该材料的应变率参数，为完善数值模拟中材料的各项参数提供参考。

1 试验准备

试验设计12组共60个试件，采用行业和国家标准规定的窄条拉伸法，试件按照《GBT1040.3-2006》中的II型样式进行加工[5]，制成长150 mm，宽50 mm，标距为50 mm的窄条试样。试验拉伸速率分别为50、100和150 mm/min。片材型号分为两种，一种为厚度1.2 mm，花纹表面片材，为了便于试验测量，花纹面片材的横截面积长宽高均用游标卡尺取最外围，即厚度1.2 mm为花纹片材的最大厚度。因为受到片材表面花纹的影响，花纹的实际平均厚度小于1.2 mm；另外一种为厚度2.0 mm,光滑表面片材。拉伸方向分为纵向拉伸和横向拉伸，如图1所示。

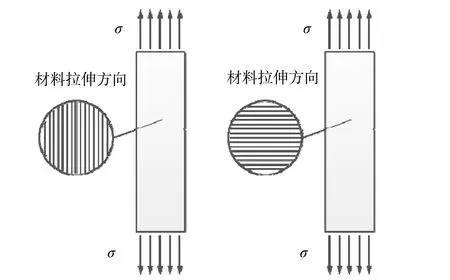
图1 HDPE片材拉伸方向示意图Fig.1 Schematic diagram of the tensile direction

2 试验现象

在试件受拉初始阶段，试件变形在弹性范围内，应力应变呈线性递增关系，如图2中OA段。在弹性变形阶段时，片材厚度变化较小，片材弹性模量基本保持不变，抗拉性能较为稳定。

随着拉伸位移的增加，进入塑性变形阶段，应力应变关系不再呈线性递增，片材开始屈服，如图AB段所示。当HDPE片材达到其最大拉伸强度后，随着拉伸位移的增加，片材所持荷载迅速降低，应力应变曲线开始下降，片材厚度变化较大，拉伸变形明显增大。同时，应力应变比值开始递减，抗拉性能下降，直至达到第二屈服点C点，如图2中BC段所示。达到第二屈服点后，HDPE片材所受应力开始稳定在一定值，该值为拉伸屈服平台应力，随着拉伸位移的增加，试件的工程应变增加，而工程应力基本不变。在随后的拉伸过程中应力应变曲线近似地表现为一条水平线段直至试件断裂或拉伸位移达到试验限定值380 mm，如图2中CD段所示。

图2 典型HDPE片材单轴拉伸工程应力应变关系Fig.2 Typical curve of engineering stress versus strain

如图3所示，通过实验结果可知，条带的断裂形式主要有3种，一种为I型断裂，该断裂形式的片材多为拉伸速率较小的横向受拉片材。随着条带在拉伸作用下不断伸长，片材中部厚度开始变薄，片材两端开始收缩，当拉伸应变达到一定值时，片材中部开始出现裂纹，韧带受拉导致片材应力集中出现材料局部“发白”。随着韧带的继续屈服，应力发白区开始扩大，裂纹尖端继续拓展，同时片材两端不断变窄。最终，两端的裂纹尖端与片材左右两端相遇，片材断裂，成典型的“八”字型断裂状态。在12组60个试样中，有36个试样断裂，其中I型断裂有12个，光面横向受拉片材在50 mm/min拉伸速率下有2个，花纹面横向受拉片材在50 mm/min和100 mm/min拉伸速率下共10个试样断裂，可见I型断裂主要发生在拉伸速率不高的横向受拉试件上。

II型断裂主要发生在高拉伸速率下的纵向受拉试件中。与I型破坏模式不同，在高拉伸速率下，裂纹初始出现位置为片材两端，而非片材中部。而后随着拉伸位移的增加，裂纹开始拓展，中心韧带有明显的应力发白现象，应力开始集中，裂纹延伸至中心韧带后，中心韧带开始延伸，此时片材的应力应变曲线仍处于屈服平台。随着中心韧带变薄，片材破坏，两端裂纹呈水平状，裂口光滑，中心断裂韧带无明显的拉伸纤维可见。在断裂的36个试件中，有12个II型断裂，均为光面纵向受拉试件，其中在100 mm/min和150 mm/min拉伸速率有10个。可见，II型断裂主要发生在高拉伸速率下的光面纵向受拉试件。

III型断裂主要发生在花纹面纵向受拉试件上，随着拉伸位移的增加，首先片材一端出现裂纹，而后裂纹逐渐拓展延伸，并没有明显应力发白区和拉伸纤维出现，而后裂纹延伸至试件另一端，试件破坏。在36个破坏试件中，有12个III型破坏，均为花纹纵向受拉构件，与II型破坏模式对比，其主要区别为制作工艺，虽然II型破坏和III型破坏均以纵向受拉构件为主，但不同的是，II型破坏的纵向受拉构件为光面片材，而III型破坏的纵向受拉构件为花纹面片材。因此，试样的型号的确会影响片材的破坏模式，导致破坏第1阶段时，裂纹出现的位置和数量不同，最终导致片材断裂行为的不一致。

3 试验结果

HDPE片材拉伸强度值如表1所示，HDPE片材屈服平台强度值如表2所示。

图3 断裂模式示意图Fig.3 Schematic diagram of different failure model

表1 HDPE片材拉伸强度值

Table 1 The tensile strength of the HDPE specimens

拉伸速率/(mm·min-1)横向拉伸片材样式拉伸强度/MPa纵向拉伸片材样式拉伸强度/MPa横向拉伸片材样式拉伸强度/MPa纵向拉伸片材样式拉伸强度/MPa50光面15 58光面14 40花纹面21 66花纹面19 26100光面15 92光面14 58花纹面22 38花纹面20 20150光面16 02光面14 87花纹面23 09花纹面21 02

表2 HDPE片材屈服平台强度值

4 力学性能分析

4.1 片材样式影响分析

图4至图9为不同工况下HDPE片材在单轴拉伸试验中的工程应力应变曲线。由表1可知，花纹面片材的拉伸强度较光面片材的拉伸强度高。对于横向受拉片材，花纹面的拉伸强度比光面平均高出41.24%；对于纵向受拉片材，花纹面的拉伸强度比光面平均高出37.89%。根据实验结果，分析花纹面拉伸强度比光面拉伸强度高的原因主要有两点：① 压花工艺使得花纹面的横截面积大大减小，而中心片材的基本强度不变，故单位面积内片材所能承受的最大应力较光面片材大；② 压花工艺在热压过程中对HDPE片材的密度有所提高，故花纹面片材的拉伸强度较光面HDPE片材的拉伸强度较高。

虽然花纹面的拉伸强度较光面片材高，但是对于单个片材，光面片材所能承受的最大荷载平均为766 kN，而花纹面片材所能承受的最大荷载平均为650 kN。此外，在拉伸变形较大的情况下，花纹片材的稳定性更差，较易断裂，且随着拉伸速率的上升，花纹片材的应力屈服平台随拉伸速率提升而提升的现象不明显，即率相关性不明显。由此可知，光面片材适用于荷载大，持荷时间较长的工程运用中，而花纹面片材适用于重量轻，持荷时间较短的工程。

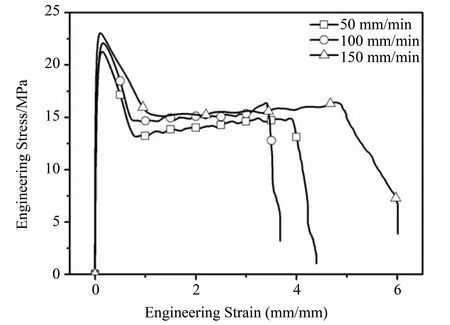
图4 不同拉伸速率下花纹横向受拉片材工程应力应变曲线Fig.4 The engineering stress versus strain curve of the transverse tensile pattern specimen under different stretching speed

图5 不同拉伸速率下花纹纵向受拉片材工程应力应变曲线Fig.5 The engineering stress versus strain curve of the longitudinal tensile pattern specimen under different stretching speed

4.2 拉伸方向影响分析

对于花纹面片材，由图4和图5可看出，花纹横向受拉片材和纵向受拉片材的最大拉伸应力的率相关性均不明显，且屈服平台强度的率相关性也不明显。但与纵向受拉片材相比，横向受拉片材的伸长率较纵向受拉高。对于光面片材，通过图6和图7的对比可知，纵向受拉片材和横向受拉片材最大拉伸强度随拉伸速率的增加而增加的现象不明显，即最大拉伸强度的率相关性不明显。但与纵向受拉片材不同的是，横向受拉片材随拉伸速率的上升，其屈服平台逐步上升，屈服平台强度增大。当拉伸速率为150 mm/min时，光面横向受拉片材的屈服平台与曲线最高点之间没有明显的下降段，第二屈服点不明显，应力应变曲线在到达最大拉伸强度后没有明显下降。此外，纵向受拉片材的断裂数量比横向受拉片材断裂的数量多。

图6 不同拉伸速率下光面横向受拉片材工程应力应变曲线Fig.6 The engineering stress versus strain curve of the transverse tensile smooth specimen under different stretching speed

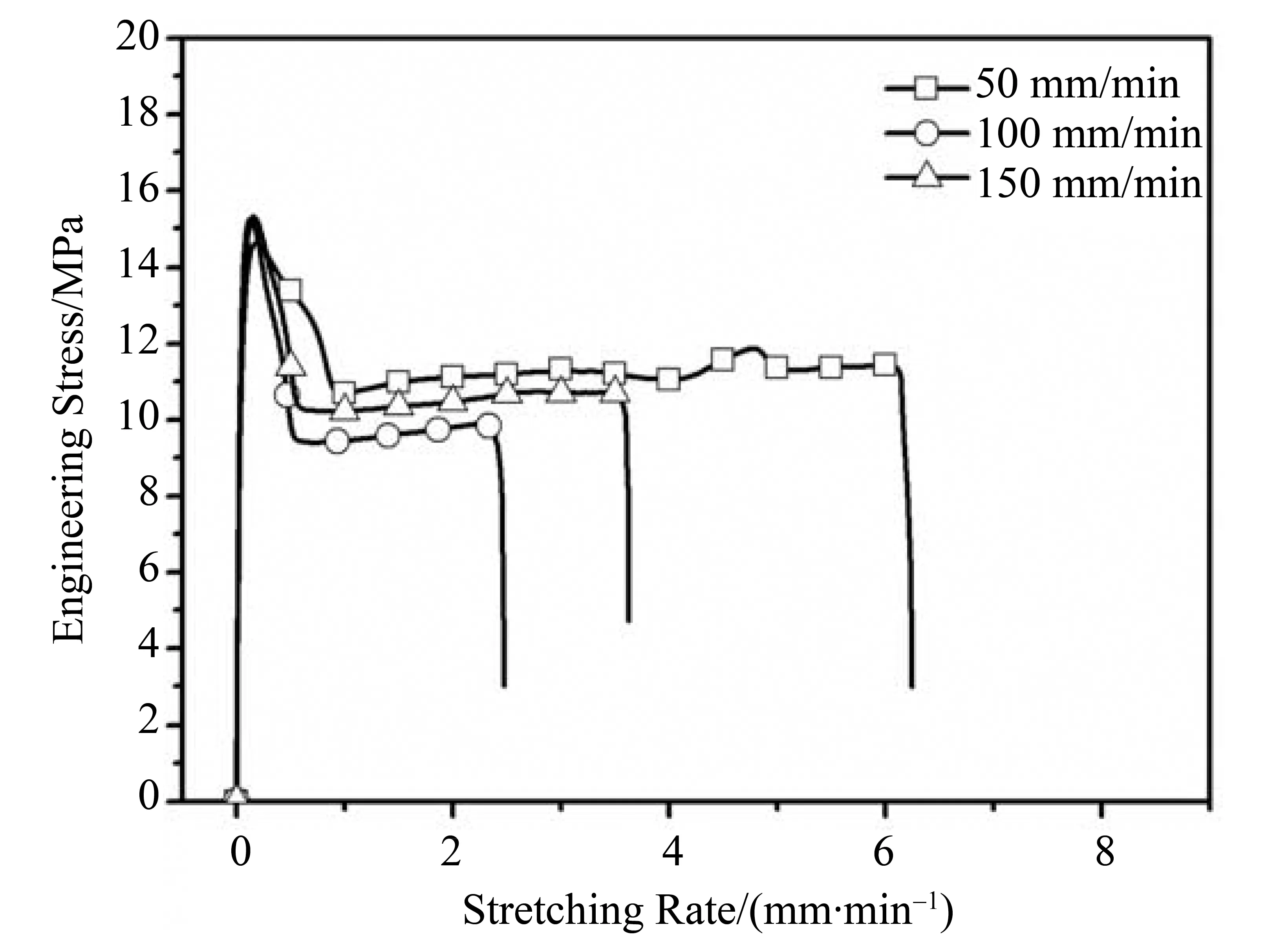
图7 不同拉伸速率下光面纵向受拉片材工程应力应变曲线Fig.7 The engineering stress versus strain curve of the longitudinal tensile smooth specimen under different stretching speed

图8 不同拉伸速率下HDPE片材的最大拉伸强度Fig.8 The maximum tensile stress of the specimen under different stretching speed

图9 不同拉伸速率下HDPE片材的屈服平台强度Fig.9 The second yield value of the specimen under different stretching speed

4.3 拉伸速率影响分析

由图8可看出HDPE片材的拉伸强度随着拉伸速率的提高，光面片材的最大拉伸强度没有显著的变化。根据文献[4]，在低拉伸速率下，HDPE片材单轴拉伸性能的率相关性表现较为明显。但图8表明，在拉伸速率大于50 mm/min后，光面HDPE片材拉伸强度的率相关性不明显，其拉伸强度随拉伸速率增加平均增加1.37%。与光面片材相反，花纹面片材拉伸强度的率相关性较光面片材更为明显，拉伸强度随拉升速率的增加平均增加5.02%。但从图9中可看出随着拉伸速率的上升，光面横向受拉片材屈服平台强度值上升较为明显，在拉伸速率为150 mm/min时，屈服平台上升至15.23 MPa，接近于其拉伸强度。以上现象表明，当拉伸速率较大时，HDPE片材的拉伸强度的率相关性较为不明显。对于光面横向受拉片材，其屈服平台值的率相关性较为明显。

5 结论与展望

1)HDPE试样型号和试验拉伸速率对片材的断裂形式有影响。对于光面片材，当拉伸速率为50 mm/min和100 mm/min，试样的断裂形式主要为I型断裂；在拉伸速率为150 mm/min，光面片材的断裂形式主要为II型断裂。其次，对于花纹面片材，其断裂形式主要以III型断裂为主。

2)在拉伸速率大于50 mm/min时，光面横向受拉片材的屈服平台强度具有较明显的率相关性。花纹面片材最大拉伸强度的率相关性较明显。

3)试验反映出来的工程应力应变曲线可为本构方程的验证提供数据参考。因篇幅限制，本构公式的研究及数值模拟于另外一篇文章中进行详细阐明。

4)通过HDPE片材的霍普金森拉杆试验所得数据，并结合本文试验，可以拟合得出应变率效应参数，进而完善数值模拟中的材料参数和本构方程。

[1] G’SELL C, JONAS J J. Determination of the plastic behavior of solid polymers at constant true strain rate[J]. Journal of Materials Science, 1979,14 (3): 583-591.

[2] KWON H J, JAR P Y B. On the application of FEM to deformation of high-density polyethylene[J]. International Journal of Solids and Structures, 2008,45: 3521-3543.

[3] ZHANG Y, JAR P Y B. Phenomenological modelling of tensile fracture in PE pipe by considering damage evolution[J]. Materials and Design, 2015,77: 72-82.

[4] 李俊伟，黄宏伟. 土工格室HDPE片材拉伸应变率相关特性[J]. 建筑材料学报, 2008,12(1):47-51.

[5] 中国国家标准化管理委员会.GB/T 1040.3-2006 塑料拉伸性能的测定 第3部分：薄膜和薄片的试验条件[S].北京：中国标准出版社，2006.

[6] 石少卿,刘颖芳,尹平. 硬质聚氨酯泡沫塑料在军事工程中的应用技术[J]. 工程塑料与运用, 2004,32(8): 36-39.

[7] KHEDRI S, EIYASI S. Kinetic analysis for thermal cracking of HDPE: A new isoconversional approach[J]. Polymer Degradation and Stability, 2016,129:306-318.

[8] BHARATH K B R, DODDAMANI M. Data characterizing tensile behavior of cenosphere/HDPE syntactic foam[J]. Data in Brief, 2016,06:933-941.

[9] 刘浩，张亚芳，齐雷. 短纤维增强脆性基复合材料破坏过程和力学性能研究[J]. 中山大学学报(自然科学版), 2008,47(6): 124-128.

[10] KWON H J, JAR P Y B. On the application of FEM to deformation of high-density polyethylene[J]. International Journal of Solids and Structures, 2008,45: 3521-3543.

[11] GUO Lingmei, LV Yanan, DENG Zhifang. Tension testing of silicone rubber at high strain rates[J]. Polymer Testing, 2016,50: 270-275.

[12] 汤先文，郭卫红，高原冀,等. 新型PET超韧性工程塑料的制备[J]. 中山大学学报(自然科学版), 2005,44(z2): 39-41.

[13] 顾良军，杨晓华. 土工格室结构层拉伸性状试验研究[J]. 公路交通科技, 2007,24(1): 38-42.

[14] 马定洋，章林溪. 拉伸分子动力学方法研究聚乙烯单链的力学行为[J]. 高分子学报, 2008,(5): 448-453.

[15] 黄西成，陈裕泽，朱建士. 缺口试件拉伸试验中的材料失效函数确定方法[J]. 固体力学学报, 2008,29(4): 385-388.

The mechanism property analysis of the uniaxial tensile experimental about the high density polyethylene

CHENZipeng1,2,SHIShaoqing1,2,LUOWeiming1

(1. Department of Civil Engineering, Logistical Engineering University, Chongqing 401311, China 2. Chongqing Key Laboratory of Geomechanics & Geoenvironmental Protection,Chongqing 401311, China)

Since the high density polyethylene(HDPE) is popularly used in areas such as the chemistry, construction and the military project, the types and the conditions for usage are verified. The uniaxial tensile test on the smooth surface specimens and the pattern surface specimens is performed, with different stretching speed and tensile directions. The experiment shows that the yield platform value of the smooth specimens also increases with the increase of the stretching speed, which is under the transversal tension. When the stretching speed is 150 mm/min, the smooth transversal tensile specimen has inconspicuous second yield point, which means that it has better performance on the tension. The rate dependence of the pattern specimens is more obvious and its value is 5.02% under 3 different stretching speed. However, the load the pattern specimens can undertake is lower contrast with the smooth specimens. It is easier for the pattern specimens to be broken than the smooth specimens, and it is also easier for the longitudinal tensile specimens to be broken than the transversal tensile specimens. Consequently, the smooth transversal tensile specimen has better tensile strength.

the uniaxial tensile test; the rate dependence; the direction dependence; the high density polyethylene

10.13471/j.cnki.acta.snus.2016.06.016

2016-06-30

全军后勤科研计划资助项目(BY211C015)

陈自鹏(1992年生)，男；研究方向：新型材料抗冲击抗爆炸；通讯作者：石少卿;E-mail:ssq601@163.com

TQ

A

0529-6579(2016)06-0103-06