基于优化最小二乘支持向量机的室内定位算法*

黄 震，罗中良，陈治明

(1. 惠州学院计算机科学系，广东 惠州 516007;2. 惠州学院电子科学系，广东 惠州 516007)

基于优化最小二乘支持向量机的室内定位算法*

黄 震1，罗中良2，陈治明2

(1. 惠州学院计算机科学系，广东 惠州 516007;2. 惠州学院电子科学系，广东 惠州 516007)

室内定位是普适计算应用中的关键技术，针对最小二乘支持向量机参数优化的难题，提出一种优化最小二乘支持向量机的室内定位算法。首先采用主成分分析提取重要定位特征，然后采用最小二乘支持向量机建立室内定位模型，并采用粒子群优化算法对最小二乘支持向量机参数进行优化，最后采用仿真实验测试定位性能。结果表明，文中算法提高了室内定位的精度且定位时间少于其它室内定位算法，具有一定的实际应用价值。

普适计算；室内定位；参数优化；主成分分析

普适计算是新一代的信息技术，集成通信技术、电子技术以及计算机技术，用户可以随时随地获取自己需求的资源，其在智能电梯、环境监控、物流管理等领域得到了成功的应用[1]。定位技术是普适计算一个比较底层的技术，在普适计算应用中扮演重要的角色，定位技术根据应用场景分为两类：室内定位和室外定位，当前在室外空旷的环境下，一些技术如GPS定位的精度相当高，可以满足实际应用的需求，但是室内环境十分复杂，障碍物多、信号有多径现象，GPS不能在室内环境中工作，导致室内定位难度增加，因此室内定位一直是无线定位技术研究中的难点[2-4]。

为了实现室内准确定位，人们引入各种技术对其进行研究，出现了一些室内定位算法。室内定位技术主要基于位置指纹进行设计，其工作过程分为两个阶段[5]：离线和在线。离线阶段主要负责“指纹”数据的采集，即将设备放在参考点收集接受信号强度指示(received signal strength indicator，RSSI)信息，构建无线信号地图，但是由于室内环境的复杂性，RSSI信息具有时变性和噪声，极不稳定，如果直接利用RSSI值作为定位算法的输入进行室内定位，定位结果可靠性差，准确性低；同时输入的RSSI信息比较多，具有严重的冗余，因此需要对RSSI值进行预处理[6-8]。当前位置指纹匹配的算法主要有神经网络、支持向量机、加权K邻居算法等[9-13]，其中加权K邻居算法最简单、十分容易实现，但是利用其进行室内定位，处理结果误差比较大差，实际应用价值不大；神经网络的室内定位精度要高于加权K邻居算法，但是其要求训练样本的数量比较多，使得室内定位成本增加；支持向量机比神经网络的室内定位精度进一步提高，要求训练样本的数量少，但是其训练时间耗时比较长，室内定位的效率低。

为了改善室内定位效果，提出一种优化最小二乘支持向量机的室内定位算法(PCA-PSO-LSSVM)。首先采用主成分分析对原始信息进行处理提取重要特征，然后采用最小二乘支持向量机(least squares support vector machine，LSSVM)对特征向量与位置信息之间的关系进行拟合，并采用粒子群优化(particle swarm optimization algorithm,PSO)算法对最小二乘支持向量机进行优化，仿真实验结果表明，相对传统定位算法，PCA-PSO-LSSVM能够获得更高精度的室内定位结果，提升了室内定位的效率，可以满足室内定位的实际应用需求。

1 RSSI模型

室内定位受到障碍物、信号多径化等多因素影响，使RSSI的变化大、不稳定，本文选择路径-损耗模型估计RSSI的值，计算公式如下：

(1)

式中，Xσ～N(0,σ2)为噪声。

对式(1)进行简化，可以得到：

(2)

式中，RSSI(d0)为与发射地点1 m的RSSI值。

d0为1 m，最后RSSI的计算公式为：

RSSI(d)=RSSI(d0)-10nlgd

(3)

式中，n为损耗系数。

2 PCA-PSO-LSSVM的室内定位

2.1 主成分分析(PCA)

采集到原始RSSI特征之后，对它们进行主成分分析。

1) 建立原始特征的向量矩阵A，具体为：

(4)

其中，n是特征总数。

2) 对A进行标准化处理，可以得到矩阵B：

(5)

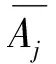
(6)

(7)

3) 计算协方差矩阵BTB， 并得到相应的特征值和向量P，且满足：

PTBTBP=Λ

(9)

(10)

4) 计算累计贡献率，取累计贡献率超过85%的特征作为主成分：

(11)

2.2 最小二乘支持向量机(LSSVM)

支持向量机计算复杂度与训练样本的数量密切相关，因此对于大规模的训练样本，支持向量机的计算复杂度相当高，训练的效率比较低，影响室内定位的实时性，而LSSVM对支持向量机的损失函数进行改进，减少待定参数，训练速度加快，应用范围更广泛。设训练样本集为：{(xi,yi)},i=1,2,…n，xi∈Rn,yi∈R，LSSVM的最优线性回归方程如下：

(12)

式中，w为权值向量，b为偏置量。

基于结构风险最小化原理可以得到：

s.t.

(13)

式中，γ为正则化参数；ei为拟合误差。

采用拉格朗日乘子(αi)对式(13)进行简化，得到：

(14)

核函数为K(xi,xj)=φ(xi)Tφ(xj)，这样可以得到：

(15)

采用RBF构建LSSVM，其为：

(16)

式中，σ为RBF参数。

LSSVM回归函数为：

(17)

2.3 粒子群优化(PSO)算法

PSO算法通过粒子追随自己历史最优解(Pbest)和粒子群的历史最优解(gbest)找到问题的最优解，粒子速度和位置的更新公式为：

(18)

(19)

式中，vid(i)和vid(id+1)分别为粒子当前和更新后的速度；xid(i)和xid(id+1)分别为粒子当前和更新后的位置；w为惯性权重；c1、c2为加速因子[14]。

在LSSVM拟合室内定位的特征向量与位置信息之间的关系时，LSSVM学习性能取决于参数γ和σ，为此本文采用PSO算法优化LSSVM，参数γ和σ优化的数学模型为：

(20)

2.4 PCA-PSO-LSSVM的室内定位

1) 确定指纹位置，并采集相应的RSSI值，建立无线电地图，采用PCA提取对室内定位结果有重要贡献的定位特征，并将其保存在特征数据库中，然后将定位特征作为输入向量和位置信息输出构建LSSVM的训练样本集，采用PSO算法选择LSSVM参数γ和σ建立拟合特征与位置关系的定位模型。

2) 对测试样本集进行处理，然后采用建立好的室内定位模型估计其位置信息。

基于PCA-PSO-LSSVM的室内定位算法框架如图1所示。

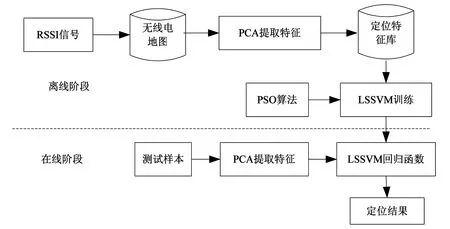
图1 PCA-PSO-LSSVM算法的框架Fig.1 Framework of the PCA-PSO-LSSVM algorithm

3 结果与分析

为了验证PCA-PSO-LSSVM的室内定位有效性，实验环境为学院大楼的室内大厅，包括过道、实验室、办公室等定位区域，每一个位置均有一些障碍物，在不同时间对每个位置点RSSI值进行采集， PCA-LSSVM(手工方式确定LSSVM参数)、PCA-GA-LSSVM(遗传算法优化LSSVM参数)进行对比测试，采用定位误差和平均定位误差对室内定位结果进行评价，计算公式为：

(21)

(22)

式中，n表示测试点的数量。

采用LSSVM拟合特征向量与位置信息之间的关系时，参数γ和σ的选择至关重要，采用PCA-LSSVM和PCA-GA-LSSVM以及PCA-PSO-LSSVM进行定位实验，参数如表1所示。定位结果如图2所示，可以得到如下结论：

1) 相对于PCA-LSSVM，PCA-GA-LSSVM以及PCA-PSO-LSSVM的定位精度均有不同程度的提高，因为其它条件相同，这种优势是因为GA、PSO算法可以找到更加合理的LSSVM参数γ和σ的值，建立的LSSVM可以更好拟合特征向量与位置信息之间的映射关系，定位结果更加可靠。

2) PCA-GA-LSSVM，PCA-PSO-LSSVM的室内定位精度更加理想，这是由于PSO算法较好的避免了GA易陷入局部极值的缺陷，难以搜索到全局最优的参数γ和σ，而PSO算法通过粒子的迭代过程中，可以找到更优参数γ和σ值，实验结果验证了PSO算法解决LSSVM参数优问题的优越性。

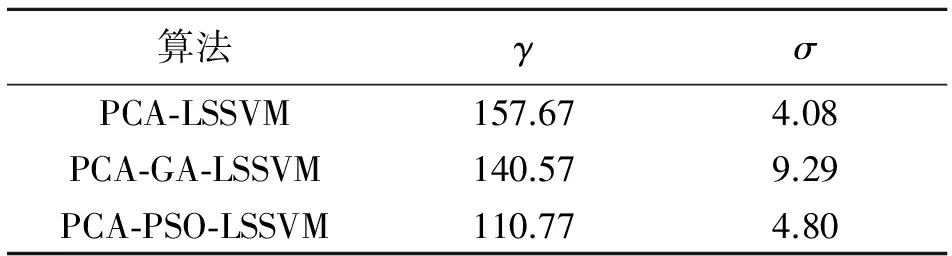
表1 LSSVM参数γ和σ的值

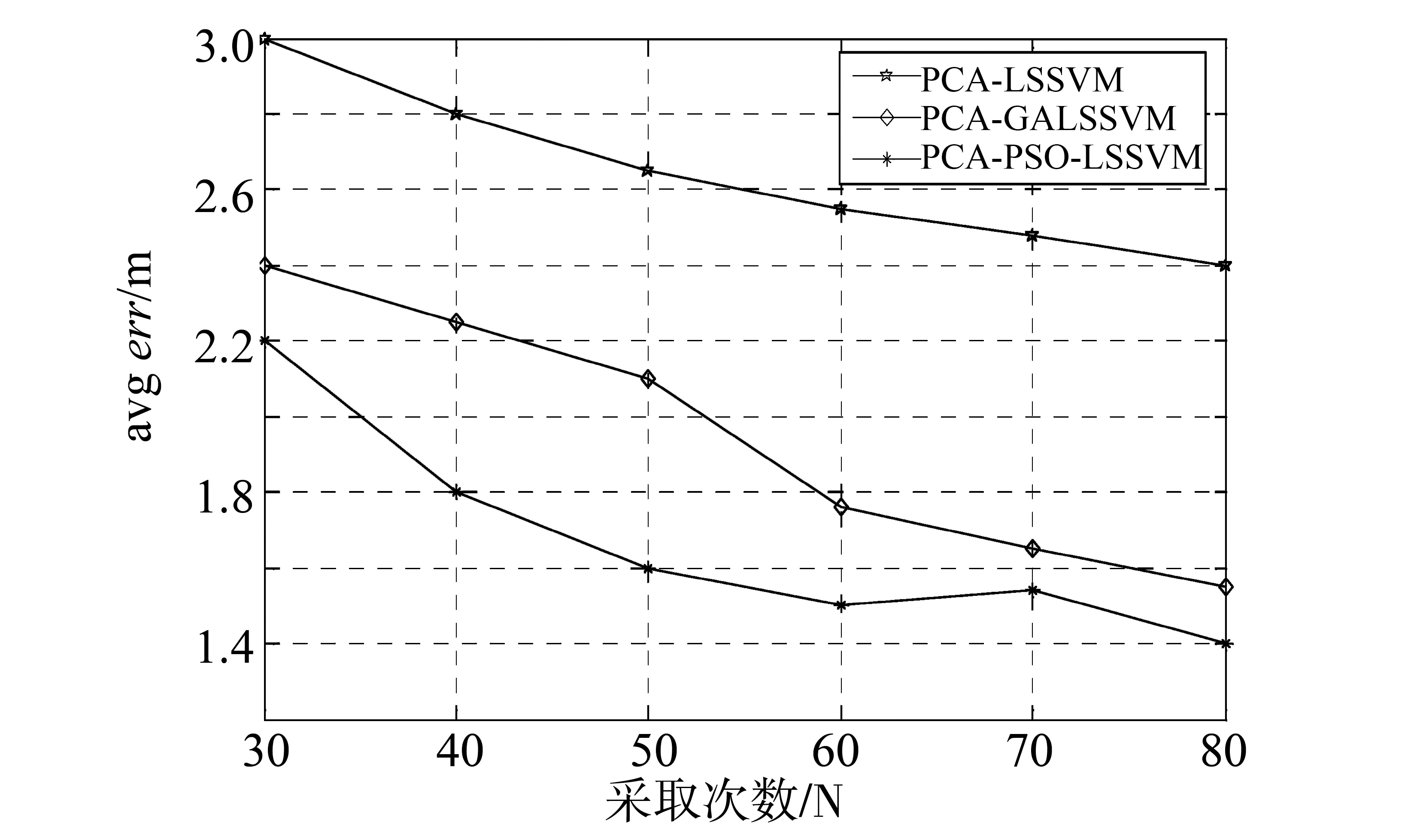
图2 PCA-PSO-LSSVM与对比算法的定位误差对比Fig.2 Location error comparison of PCA-PSO-LSSVM with other algorithms

为了测试室内定位的实时性，在4核 Intel 2.80 GHz CPU，8 GB 内存，Win7操作系统，Matlab 2012的测试平台上统计PCA-LSSVM、PCA-GA-LSSVM和PCA-PSO-LSSVM的运行时间，结果见表2。从表2的运行时间可知，PCA-LSSVM的运行时间最短，因为其是手工直接确定参数γ和σ的值，因此实时性最好，但是全凭经验设置参数，其定位精度太低，无法应用于实践；而PCA-PSO-LSSVM的运行时间要少于PCA-GA-LSSVM，主要是因为PSO算法寻优速度要优于GA，使 LSSVM的训练时间变短，定位的实时性更优，更符合室内定位要求，能给用户带来更好的室内定位结果。

表2 运行时间对比

4 结 论

针对室内定位过程中的特征提取和LSSVM参数优化难题，提出基于PCA-PSO-LSSVM的室内定位算法，该算法采用PCA提取RSSI信息中对定位结果贡献重要的特征，对数据进行一定的压缩，减少LSSVM的输入维数，然后采用LSSVM拟合特征与位置信息的非线性关系，采用PSO算法搜索最优参数，测试结果表明，PCA-PSO-LSSVM的定位精度要高于其它算法，而且运行时间更具优势，可以给用户带来更好的室内定位效果。

[1] GU Y Y, LO A, NIEMEGEERS I. A survey of indoor location systems for wireless personal networks [J]. IEEE Communications Surveys & Tutorials, 2009, 11(1): 13-32.

[2] 邓罡,陈颖文,徐明,等. 无线传感器网络环境感知的节点定位方法[J]. 中山大学学报(自然科学版), 2008, 47(6): 114-119.

[3] 孙寅博,王宏刚,李波. 基于参考标签的射频识别室内定位算法研究[J]. 电视技术,2015, 39(1): 109-112.

[4] 周锦,李炜,金亮,等. 基于KNN-SNM算法的室内定位系统设计[J]. 华中科技大学学报(自然科学版), 2015, 43(1): 517-520.

[5] 蔡朝晖,夏溪,胡波,等. 室内信号强度指纹定位算法改进[J].计算机科学,2014,41(11):178-181.

[6] 徐风燕,石鹏,王宗欣. 基于参数拟合的距离-损耗模型室内定位算法[J]. 电路与系统学报, 2009, 12(1):1-5.

[7] 张会清,石晓伟,邓贵华,等. 基于BP神经网络和泰勒级数的室内定位算法研究[J]. 电子学报,2012,40(9):1876-1880.

[8] 刘春燕,王坚. 基于几何聚类指纹库的约束KNN室内定位模型[J]. 武汉大学学报(信息科学版) , 2014, 39(11): 1287-1291.

[9] 谷红亮, 史元春.一种用于智能空间的多目标跟踪室内定位系统[J]. 计算机学报, 2007, 30(9): 1603-1611.

[10] 蒙静. IR_UWB定位系统距离误差建模及性能研究[J]. 通信学报, 2011,32(6):10-16.

[11] 林以明,罗海勇,李锦涛,等. 基于动态Radio Map的粒子滤波室内无线定位算法[J]. 计算机研究与发展, 2011,48(1):139-146.

[12] 徐玉滨,邓志安,马琳. 基于核直接判别分析和支持向量回归的 WLAN 室内定位算法[J]. 电子与信息学报, 2014, 25(11):2631-2651.

[13] 石柯, 陈洪生, 张仁同. 一种基于支持向量回归的802.11无线室内定位方法[J]. 软件学报, 2014, 25(11):2631-2651.

[14] 曾艳姗,李仲飞. 基于粒子群优化算法的均值 -VaR投资组合选择[J]. 中山大学学报(自然科学版), 2012, 51(6): 1-9.

Indoor location algorithm based on optimizing least square support vector machine

HUANGZhen1,LUOZhongliang2,CHENZhiming2

(1. Department of Computer Science, Huizhou University, Huizhou 516007 China;2. Department of Electronic Science, Huizhou University, Huizhou 516007 China)

Indoor location is a key technology in the application of pervasive computing, and aims at solving the problem of least square support vector machine parameters. An indoor localization algorithm based on the least square support vector machine is proposed. The principal component analysis is used to extract important features, and then, least square support vector machine is established for indoor localization model using particle swarm optimization algorithm. The simulation experiment is used to test location performance. The results show that the proposed algorithm improves the accuracy of indoor location, and the location time is less than other indoor location algorithm.

pervasive computing; indoor location; parameter optimization; principal component analysis

10.13471/j.cnki.acta.snus.2016.02.009

2015-11-29

广东省科技计划资助项目(2012B010100038)；广东省高等学校教学质量与改革工程本科类资助项目(粤高教函[2013]113号-113，粤高教函[2015]173号-584)；惠州市科技计划资助项目(2015ZX023)；惠州学院自然科学资助项目(hzuxl201417)

黄震(1980年生)，男 ；研究方向：无线传感器网络、智能算法；通讯作者：陈治明;E-mail:1276106@qq.com

TP

A

0529-6579(2016)02-0048-04