管路花边法兰参数的优化设计及影响分析

吴云峰，熊宴斌，刘 艳，张 萌，曾 攀



管路花边法兰参数的优化设计及影响分析

吴云峰1，熊宴斌1，刘 艳1，张 萌1，曾 攀2

（1. 北京宇航系统工程研究所，北京，100076；2. 清华大学，北京，100084）

通过对法兰进行设计，开展相应结构的有限元分析，分析了法兰锥颈角及花形设计对法兰强度和刚度的影响。结果表明，花形设计中锥颈角的增加会导致环向和轴向应力减小，对径向应力影响不大，整体法兰的刚度随锥颈角和法兰厚度的增大而增大。同时采用拓扑结构对法兰进行花形设计，优化了花形法兰设计。

花边法兰；锥颈角；花形结构

0 引 言

法兰是一种应用广泛的管道配件，它和垫片、螺栓共同组成一个密封接头体，具有连接管子、泵、阀、压力容器等各种承压设备并使之构成庞大管网系统的重要作用[1]。

法兰的结构设计直接影响结构件连接部位的密封性能，在法兰能满足强度、刚度、密封及安装要求的前提下，可以对螺栓密度、法兰外圆“花形”采用拓扑法进行结构优化[2]。本文通过对4种不同规格的法兰进行“花形”设计仿真，分析不同参数对法兰“花形”设计的影响。

1 仿真分析方法

1.1 法兰结构分析

美洲体系标准法兰如图1所示[3]。

采用Waters法对法兰强度进行分析，法兰颈部的最大轴向应力总是发生在颈部的两端，法兰盘的最大径向应力发生在内缘且与颈部连接处，法兰盘的最大环向应力发生在法兰盘内缘靠近垫片一侧。Waters法给出的校核点为图1中的K点，而非各向应力最大处的点，这是因为K点处于三向应力状态，即轴向、径向、环向应力同时存在。

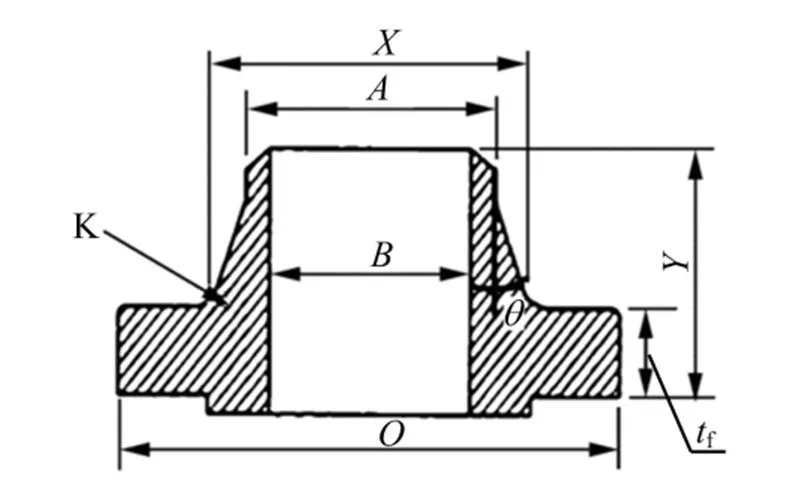
图1 美洲体系标准法兰

O—法兰外径；tf—法兰最小厚度；X—颈部大端直径；A—颈部小端外径；B—颈部小端内径；θ—锥颈角

Waters法的各向应力校核公式为

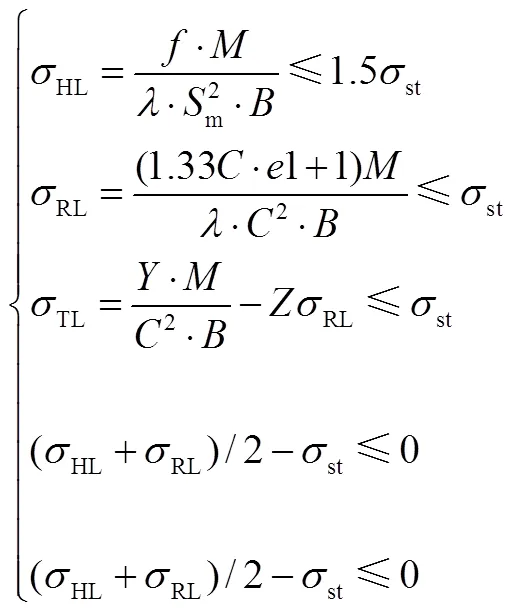
式中H，R，T分别为法兰轴向、径向和环向应力；st为法兰材料许用应力；，，，，为参数，通过查表可得；为法兰所受弯矩；m为法兰锥颈大端壁厚；为法兰盘厚度；为法兰内径。

1.2 法兰减重设计

目前，研究人员通过法兰减重设计用以优化的参数主要有法兰最小厚度f（或锥颈高度）和颈部大端直径，如图1所示。优化目标一般是于Waters法，对法兰环向应力、轴向应力以及径向应力3个方向进行控制[4]。法兰锥颈大端直径、法兰厚度f、锥颈高与三向应力的关系如图2所示[5]。由图2a可知，增加锥颈尺寸，可以降低轴向应力H和环向应力T，径向应力R随锥颈尺寸的增加变化不大；而通过图2b可知，增加法兰厚度可降低轴向应力H和环径力R，环向应力T则是先减小后增大。

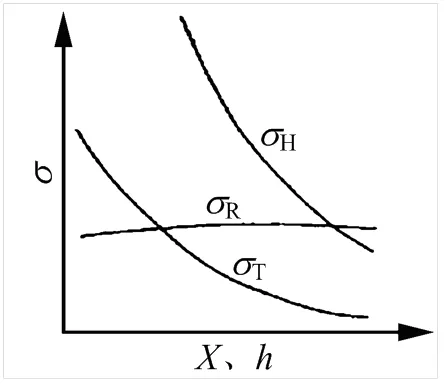
a）颈尺寸

b）厚度

图2 法兰锥颈尺寸和厚度与三向应力的关系

基于Waters法的优化分析，只能满足法兰的强度要求，而不能满足其刚度要求。法兰的刚度决定法兰的密封性能，所以这是设计中不容忽视的问题。法兰厚度的减小会导致其刚度降低，因此应保证一定的厚度值。为满足法兰刚度，法兰的最小厚度r为

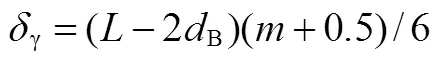
式中r为法兰厚度；为螺栓间距；B为螺栓公称直径；为垫片系数，与垫片的材料及形状有关，材料越硬，强度越高，越大。通过式（2）可以看出，要减小法兰厚度r，可以减少螺栓间距，即减少螺栓直径，增加螺栓个数。另外，采用拓扑优化将法兰盘设计为花形也是使法兰减重的重要方法。

2 模型的有限元分析

2.1 几何模型的建立

几何模型如图3所示。

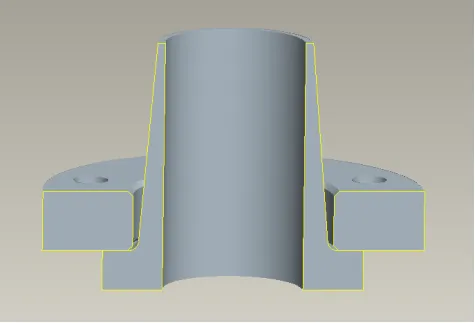
a）活套法兰与活套环

b）装配模型

图3 几何模型

因为载荷和几何条件的对称性，故采用1/2模型，并没有对垫片进行建模，而是用密封压力代替。因为法兰连接中存在较多的螺栓与法兰、法兰与法兰盘、法兰盘及活套之间的接触，因此，不宜采用二次单元。

缩减积分单元适用于接触分析，且计算速度快，在积分点求解精度高，因此本文采用缩减积分单元C3D8R[6]。

法兰计算参数见表1。

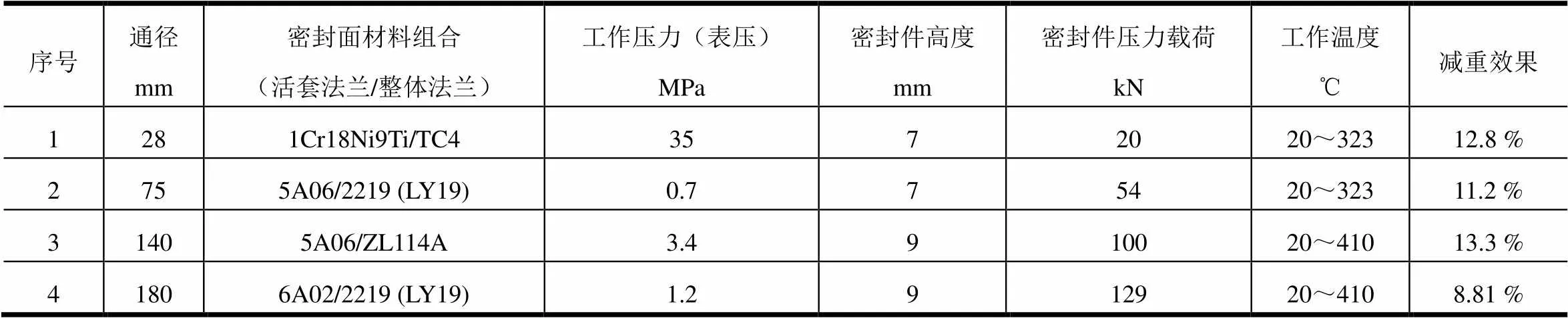
表1 4种法兰规格

计算分析的关键是要消除结构的刚体位移，位移的固支约束施加位置对最后计算结果的影响很大，法兰的工作过程如图4所示[7]。考虑到在变形过程中上下法兰在内缘变形很小，所以在分析中对整体法兰内缘附近的一段小截面施加固支约束。螺栓与螺母之间通过绑定连接来近似模拟螺纹连接，法兰盘之间、法兰和活套之间以及螺栓和法兰之间建立接触对。理论上，对螺母施加固支约束，通过接触可消除刚体位移。但在实际计算过程中，直接通过接触消除刚体位移可能会使系统不稳定而难以收敛，所以在分析中采用多个子步，对活套法兰及整体法兰施加临时固支，在计算过程中，逐步放开固支条件，并在最后一个子步只对螺栓施加固支条件。

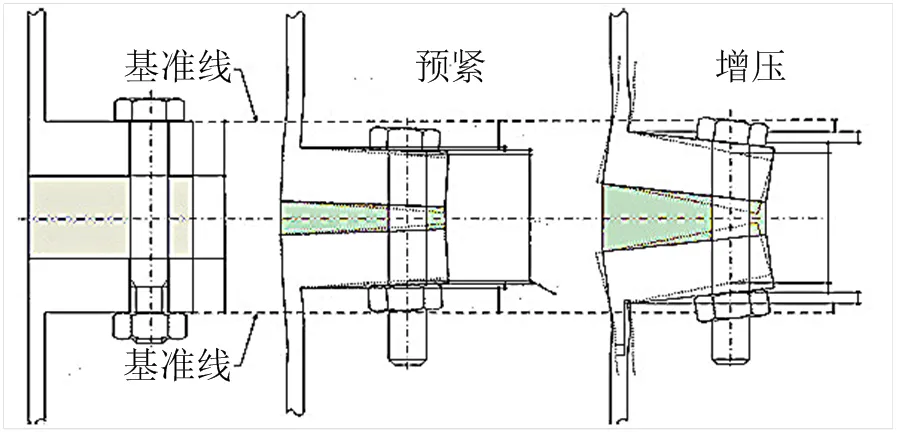
图4 法兰工作过程

2.2 仿真分析

工作条件下法兰的受力情况如图5所示[8]。图5中t是由工作内压引起的力。

图5 法兰受力情况

工作内压；f—螺栓给法兰的预紧力；轴向力；弯矩；c—垫片给法兰的密封压力

2.2.1 法兰锥颈角及厚度的影响分析

法兰锥颈及厚度尺寸对三向应力的影响在图2中已有阐明。由图2可以看出，当法兰高度一定时，锥颈高度的增加势必导致法兰厚度f减小，而锥颈高度和法兰厚度f对三向应力的影响基本相反。这是因为，当厚度增大时，相应的法兰颈锥大端的壁厚就会减小，厚度增大有利于应力减小，而壁厚减小却又会使应力增大。对于法兰锥颈角度参数，锥颈角越大，法兰锥颈大端直径则越大，可以说高度一定时，这2个参数是等价的。为达到减重目的，应在强度范围内，尽可能的减小锥颈角。

按照Waters强度校核理论，以质量为优化目标时，可列出以下表达式。

目标函数：

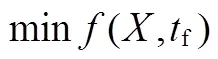
约束条件：

（4）

利用MATLAB对通径为28 mm的法兰厚度f及法里纳锥颈大端直径进行优化，得到法兰厚度f，法兰锥颈大端直径的优化值f=25.6 mm，=64 mm。如果有最小锥颈角的限制（≥3º），相应的≥67.1 mm，则相应的优化结果为=67.1 mm，f=25.6 mm。

为此，本文对通径为28 mm规格，法兰厚度f为12 mm以下的4组不同厚度值以及3种不同锥颈角的法兰在ABAQUS 6.8上进行了模拟分析，考察了图1中整体法兰K点的三向应力及密封槽处结构的刚度。分析结果如表2～5、图9、图10所示。

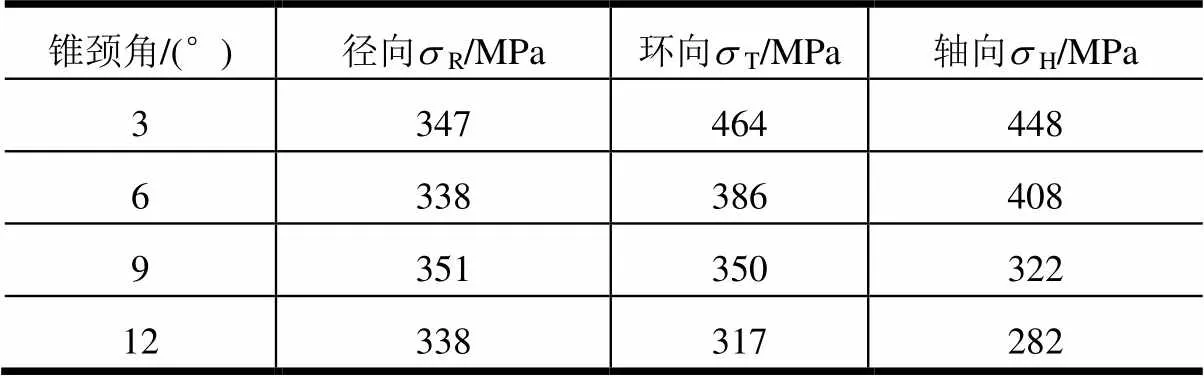
表2 不同锥颈角的整体法兰三向应力值（tf=10 mm）

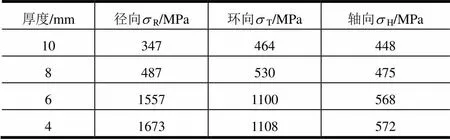
表3 不同厚度的整体法兰三向应力值（q =3°）

表4 不同锥颈角的整体法兰密封槽处最大位移值（tf=10 mm）

表5 不同厚度的整体法兰密封槽处最大位移值（q =3°）

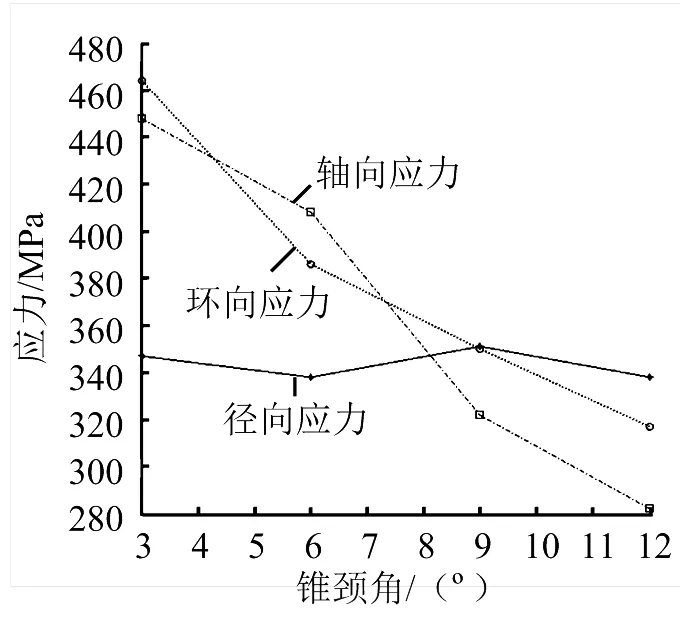
a）应力随锥颈角变化

b）应力随厚度变化

图9 通径为28mm整体法兰应力变化

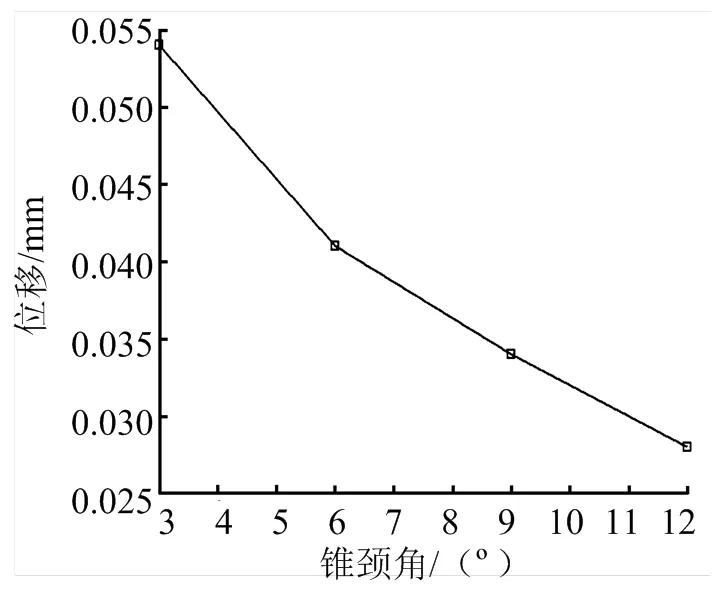
a）最大位移随锥颈角的变化

b）最大位移随厚度的变化

图10 通径为28mm整体法兰密封槽处最大位移的变化

由图9a可以看出，锥颈角的增加会导致环向和轴向应力的减小，对径向应力影响不大。当厚度减小到 8 mm时，通径为28 mm法兰仍满足强度要求，而当厚度减小到6 mm以下时，法兰不满足强度要求。

由图10a可以看出，整体法兰的刚度随锥颈角和法兰厚度的增大而增大。法兰密封槽处的位移在厚度为4 mm和6 mm时一样大，是因为法兰在其厚度小于6 mm后，均已超出其屈服强度。

2.2.2 法兰花形优化设计

采用ANSYS 13.0对通径为28 mm不带花边法兰的1/16模型做拓扑优化分析，问题描述如下：

a）目标函数：法兰质量最小；

b）约束条件：整个系统刚度最大。

计算结果的伪密度云图如图11所示。由图11可知，伪密度越小的区域对结构的刚度影响越小，在减重设计中越可以去掉。

在强度方面，在ABAQUS 6.8上对通径为28 mm不带花边的整体法兰进行了计算，Mises受力云图如图12所示。

利用刚度、强度分析的结果来指导花边设计，最终确定如图13所示的花边半径2为由原先的14 mm改为5.7 mm，体积减小约1 000 mm3。

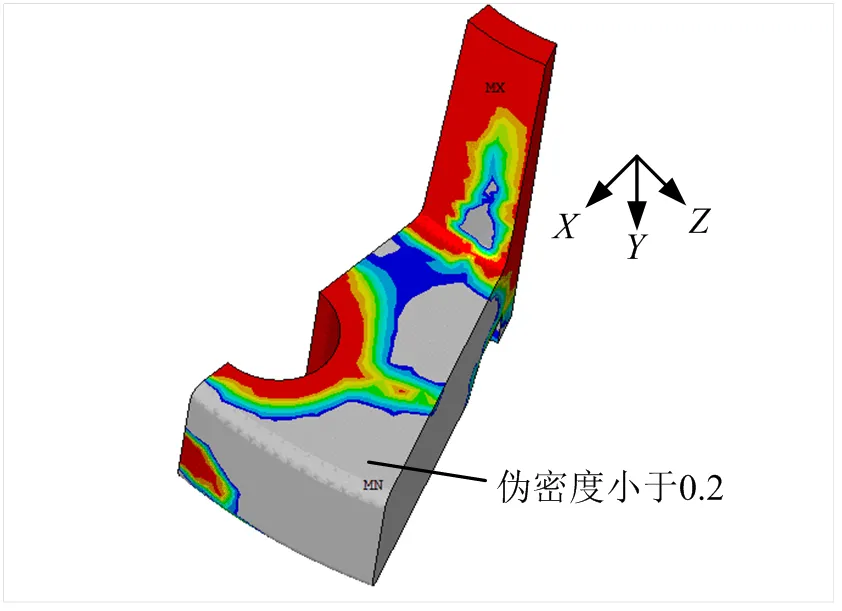
图11 以刚度为约束的法兰拓扑优化

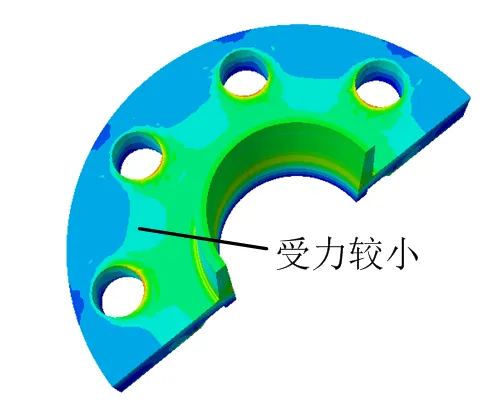
图12 不带花边整体法兰Mises受力云图

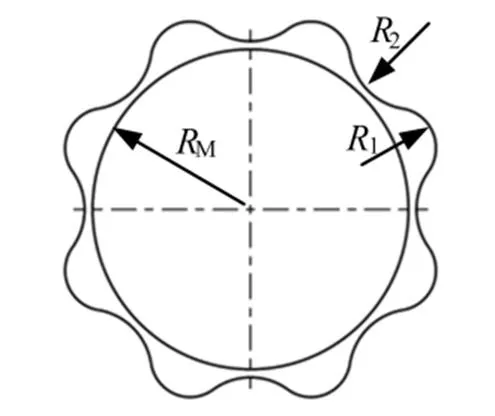
图13 花边法兰俯视图

对修改后的模型进行计算，结果分别如图14、 表6所示。

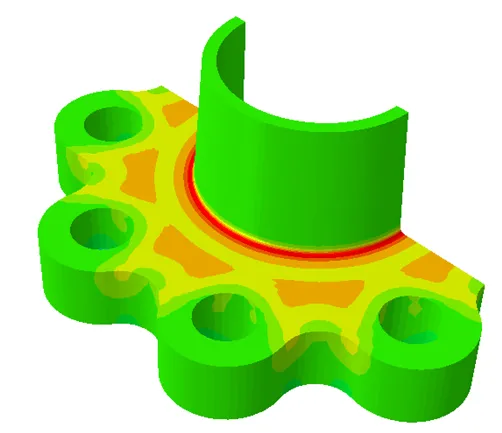
a）径向

b）环向

c）轴向

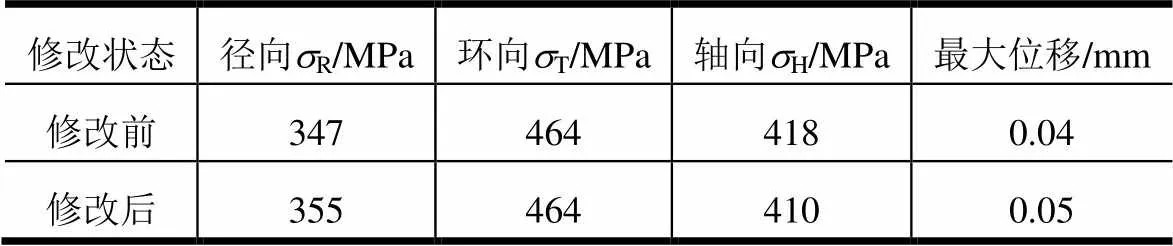
表6 花边修改前后法兰三向应力和最大位移

从图14、表6可以看出，修改后的模型在强度和刚度方面与修改前改变很小，符合设计要求。

3 结 论

通过对模型的计算结果分析，得出以下结论：

a）对于整体法兰、活套法兰及活套环，法兰三向应力与法兰的具体厚度、锥颈角等有很大影响；

b）对于整体法兰和活套法兰，法兰的最大轴向、径向及环向力基本分布在法兰盘和法兰锥颈的交接处，这与Waters理论相符合，也说明Waters理论选择这一区域附近的点作为校核点是符合实际情况的；

c）随着法兰锥颈角的增大，轴向应力和环向应力会随之减小，径向应力变化不大，在一定范围内，法兰厚度的增大可有效减小三向应力；

d）通过上述计算，证明花边法兰方案的合理性，同时根据拓扑方法得到合适的法兰花边尺寸，并对法兰的整体性能影响较小。

[1] 周明衡, 常德功. 管路附件设计选用手册[M]. 北京: 化学工业出版社，2004.

[2] 郑晓亚, 徐超等. 螺栓-法兰连接结构非线性优化设计方法研究综述[J].强度与环境, 2008, 35（3）: 7-13.

[3] 梁丰收. 标准管道法兰强度计算及有限元分析研究[D]. 合肥: 合肥工业大学, 2005.

[4] 全国压力容器标准化技术委员会. GB150-1998，钢制压力容器[S]．北京: 中国标准出版社，1998．

[5] 李世玉, 桑如苞. 压力容器工程师设计指南[M]. 北京: 化学工业出版社, 1994.

[6] Dassault Systemes Simulia Corporation. Abaqus Analysis User’s Manual[M]. Pairs: Dassault Systemes Simulia Corporation, Providence, 2012.

[7] Bouzid A H, Galai H. A new approach to model bolted flange joints with full face gaskets[J]. Journal of Pressure Vessel Technology, 2011(133): 1-7.

[8] 孙世锋, 蔡仁良. 承受外弯矩作用的法兰接头有限元分析[J]. 压力容器, 2003, 120(12): 19-26.

Optimal Design and Effect Analysis of Pipe Lace Flange Parameter

Wu Yun-feng1, Xiong Yan-bin1, Liu Yan1, Zhang Meng1, Zeng Pan2

(1. Beijing Institute of Aerospace Systems Engineering, Beijing, 100076; 2. Tsinghua University, Beijing, 100084)

Through optimal design and finite element analysis, the effect on flange intensity and rigidity of flange taper angle and lace configuration were evaluated. The results indicate that as flange taper angle increases, circumferential stress and axial stress decreased, while radial stress changed less, the rigidity of integral flange grows up as flange taper angle and flange thickness increased. Through topological structure design, the optimal lace flange configuration was obtained.

Lace flange; Flange taper angle; Lace configuratio

1004-7182(2016)03-0093-05

10.7654/j.issn.1004-7182.20160322

V414.19

A

2015-07-20；

2015-11-16

吴云峰（1985-），男，工程师，主要研究方向为飞行力学