三支聚类分析
于洪
三支聚类分析
于洪*
(重庆邮电大学计算智能重庆市重点实验室,重庆 400065)
受三支决策理论的启发,该文介绍了一种新的聚类策略,即三支决策聚类,简称三支聚类。在三支聚类分析中,类簇不再用一个集合表示,而是用两个集合来表示。这两个集合分别叫做这个类的核心域和边缘域。位于核心域的对象是类中的典型对象;位于边缘域中的对象是类中的边缘对象,他们可能属于这个类,也可能不属于这个类。这种三支表示既能够处理传统的硬聚类也能处理软聚类任务。随后,该文介绍了基于评价函数的三支决策聚类模型,并给出一种基于k-means的三支决策聚类方法作为实例分析。最后,该文综述了近年来三支聚类方面的研究成果以及发展方向。
聚类;三支决策;不确定性;硬聚类;软聚类
引言
聚类是一种无监督的学习方法被广泛地应用到各个领域,如信息检索、图像分析、生物信息处理、网络结构分析以及很多其它应用[1]。一般地,现实世界充满了不确定性。例如,在网络服务中,用户的兴趣是会改变的,兴趣社区也是多变的。
人工智能和认知科学的研究揭示了人类智能的特征,即在认识和处理现实世界问题时,人类经常从不同的层面或者粒度来观察和分析同一问题。聚类的过程反映了在不同层面做决策的过程。也就是说,聚类是一个在一定粒度层面确定对象属于或者不属于一类的过程。
设由若干对象组成一个论域,如图1 所示。对应于最细粒度的聚类结果是每个对象单独成为一个类;对应于更粗粒度的聚类结果是这里有两个类;对应于最粗粒度的聚类结果是所有的对象组成一个类。聚类过程中如果信息足够充分,可以得到某一粒度下确定的聚类结果;如果信息不过充分就无法判定对象是否确定属于某个类,需要更多的信息来做最终的决策。

图1 数据集示意图
观察图1在一定的粒度层面下,论域中存在两个明显的类。如图2 所示黄色部分为一个类,红色部分为一个类。观察对象x1和x2,它们可能属于黄色的类也可能属于红色的类。一个解决方法是把这些对象确切地划分到不同的类中,如软聚类、重叠聚类或者模糊聚类。换而言之,一个对象可以属于不同的类。

图2 聚类示意图
观察对象x3和x4它们应该属于黄色的类,x5和x6应该属于红色的类,如图3所示。这是一种典型的二支决策聚类结果,即对象确定属于一个类或则确定不属于一个类。然而,二支决策聚类结果不能直观地反映对象x3和x4是黄色类的边缘对象这一事实。同理,对象x5和x6是红色类的边缘对象。图4展示了三支聚类结果,x1、 x2、x3和x4被划分到黄色类的边缘区域。x1、 x2、x5和x6被划分到红色类的边缘区域。

图3 二支聚类结果
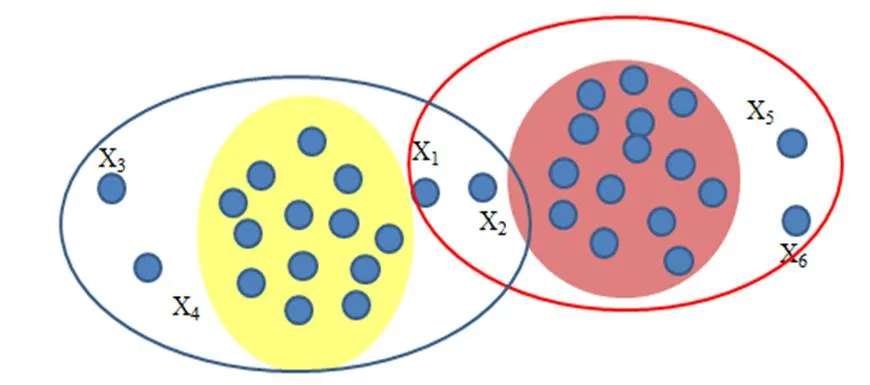
图4 三支聚类结果
人们通常根据已有的信息和证据做决策。然而,信息的获取通常是一个动态的过程。由于当前信息不充分,不能确切地知道对象的类别归属,提供了另外一种方案来处理这种带有不确定性现象的聚类任务。对于那些当前很难做出决策的对象,根据当前知识系统的规则,可以提供一种二支决策结果。也可以提供一种三支决策结果,对于信息充分的对象做出确切的决策;对于信息不够充分的对象待获取信息后作进一步决策。这是一种典型的三支决策思想。
三支决策方法用三个域而不是两个域来表示概念。尽管在其它领域中得到研究,三支决策方案并没有明确的机器学习和规则归纳原理。在基于三支决策的聚类分析中,对象和类存在三种关系:1)对象确定属于一个类;2)对象确定不属于一个类;3)对象可能属于也可能不属于一个类。这是一种典型的三支决策过程来确定对象和类之间关系。这些关系促使在本文中引入三支决策思想来处理聚类分析问题。
1 相关工作
聚类分析的一个广泛潜在假设是一个类可以用一个单一的集合来表示,或者说类的边界是确定的、清晰的。类的边界是确定的可能更便于聚类结果的分析与应用,但是在一些具体应用中也显得不是那么合理。比如,在兴趣网络中,一方面一个成员很可能有多个兴趣爱好,另外一方面,一个成员对这些不同的兴趣的爱好程度是不同的。
模糊聚类中假定一个类由一个模糊集合来表示,模拟了一个逐渐变化的边界[2]。模糊聚类定量地描述类的边界,而不是定性地描述类的边界,不能很好地反映聚类结果的结构特征。为了解决这个问题Lingras和他的合作者研究了粗糙聚类和区间聚类[3,4]。Yao等人[5]用区间集而不是单一的集合来表示一个类。Chen和Miao[6]在Rough k-means中,通过合并区间集来表示聚类。基本思想是用一对上边界和下边界来表示一个类。采用一对集合来表示一个类,定性地描述一个类。
本文的一个目的就是采用两个集合来表示一个类,从而来扩展聚类分析。这促使引入三支聚类分析。位于核心域的对象是类中的典型对象;位于边缘域的对象是类中的边缘对象。换而言之,一个类用一个核心对象集合和一个边缘对象集合来表示。
三支决策思想被广泛地应用到许多领域和学科,包括医疗决策、社会判断原理、统计学中的假设测试、管理科学以及论文评审过程。因此,姚一豫教授[7][8]介绍并研究了三支决策的概念,包括正规则、边界规则和负规则。三支决策由三个域组成,对不同的域采用不同处理方式和决策方式。
最近,三支决策方法在一些领域中取得了一定成果,如决策、来及邮件过滤、聚类分析等等[9-13] [14-16]。也做了一些基于三支决策的研究工作[16,17- 19] [20-21]。本文首先对三支聚类进行形式化描述,然后给出一个基于k-means的三支决策聚类实例。
2 三支聚类分析框架
2.1 三支聚类表示
Vladimir Estivill-Castro指出类不能够被精确定义,这也是为什么有如此多的聚类算法的原因之一[4]。类的广泛命名是:一组数据对象。聚类就是把对象进行分组,相较于不同组中的对象同一组中的对象更相似。
在现有的研究工作中,聚类结果中的类被表示为一个单一的集合,即。从决策的观点来看,单一的集合表示集合中的对象确定属于这个类,不在该集合中的对象确定不属于这个类。这是一种典型的二支决策结果。硬聚类中一个对象只能属于一个类;软聚类中对象可以属于多个类。然而,这种表示并没有表明那些对象可能属于这个类,不能够反映对象对类形成的影响程度。如前文所述,用三个域来表示一个类比用一个集合来表示一个类更合适。这直接产生了基于聚类解释的三支决策。
相对于一般的二支决策的类的表示形式,提出类的三支表示形式:

(2)
这些子集满足如下性质:

另一方面,定义一个类,满足如下性质:
三支聚类结果表示如下所示:

显然,一个二支聚类结果可以表示如下:
(6)
2.2 基于评价函数的三支聚类模型
本小节介绍一种基于评价函数的三支聚类模型,根据评价函数和评价函数上的一对决策阈值来产生三个域。

(8)
基于前文的表述,可以用如下公式来表示软聚类和硬聚类:
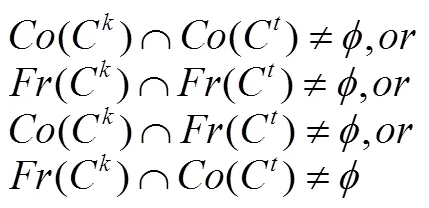
3 一种基于k-means的三支聚类方法
3.1 对象和多个类之间的划分关系
这一小节提出一种基于k-means的三支决策聚类算法。在聚类分析中可以从以下两个方面来考虑一个类的组成:一方面考虑类和类之间的关系,如果类中对象只和一个类关系紧密,那么该对象确定属于这个类,属于类的域;如果对象和多个类的关系都在一定程度上紧密,那么这个对象可能同时属于这几个类,是类中的非典型对象,应该同时属于这几个类的域。另一方面,考虑类中对象之间的关系,类中有大部分对象相互之间联系很紧密,构成类的核心部分,属于类的域,少部分对象和类中大部分对象之间的联系相对较弱,是类的关键部分,属于该类的域。
传统的硬聚类方法要求对象只能划分到唯一确定的类中,但是存在对象和多个类簇都有着密切联系的情况,这种情况下对象可能同时属于这几个类簇。这些对象可能是类间的重叠部分,这时把这些对象划分到这些类的域中更为合理,如图5所示。
3.2 对象和单个类的关系

图6 同一类中不同对象之间的差异性
同一类中的对象之间的关系也会存在强弱不同的情况,对类的形成起着不同的作用。一个类域中的对象为类中的核心部分,域中的对象是类中的重要部分,如图6所示。
直观上,类中的对象可以分为两个部分,即图中呈三角形的那部分对象是一个部分,呈圆形的那部分对象是另一个部分。图中少数呈三角形的对象明显远离呈圆形的对象,呈三角形的那部分对象可能属于类,也可能不属于类。对类中的对象进一步区分,可以把呈三角形的对象划分到类的域中,呈圆形的对象划分到类的域中。
基于以上考虑,文中采用类中对象到类中心的距离的差值对类中对象作进一步区分。考查对象和类,依次计算对象到类中心的距离,并按值从小到大排列,得到呈升序排列的序列、、、…、、。然后,依次计算这些距离的差值、、…、,找到第一个距离差值最大的对象对,和,那么把对象划分到类的域,把及其后的对象划分到类的域中。
3.3 算法描述
输入:数据集、近邻数。
Step1 初始化,指定距离数目;
Step5 如果聚类中心不发生变化,转自Step6;否则转至Step3;
Step6 考查对象和类、、。如果,那么。
Step7 对于类中剩余非域中对象,根据差值排序法,找到第一个距离差值最大的对象对,和,把及其后的对象划分到;
Step8 算法结束,输出结果:
3.4 实验结果
为了直观展示文中提出三支决策聚类和传统二支聚类算法的不同之处,在4个二维人工数据集D1 、D2 、D3和 D4上进行行实验,实验结果如图7-10所示。
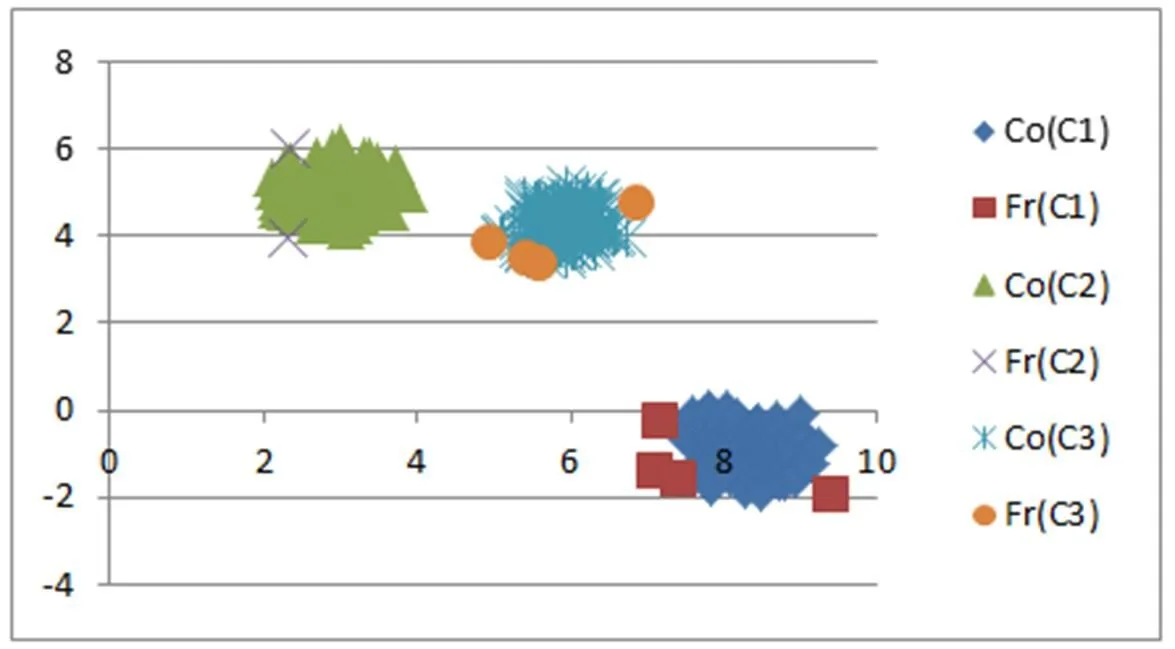
图8 数据集 D2上实验结果
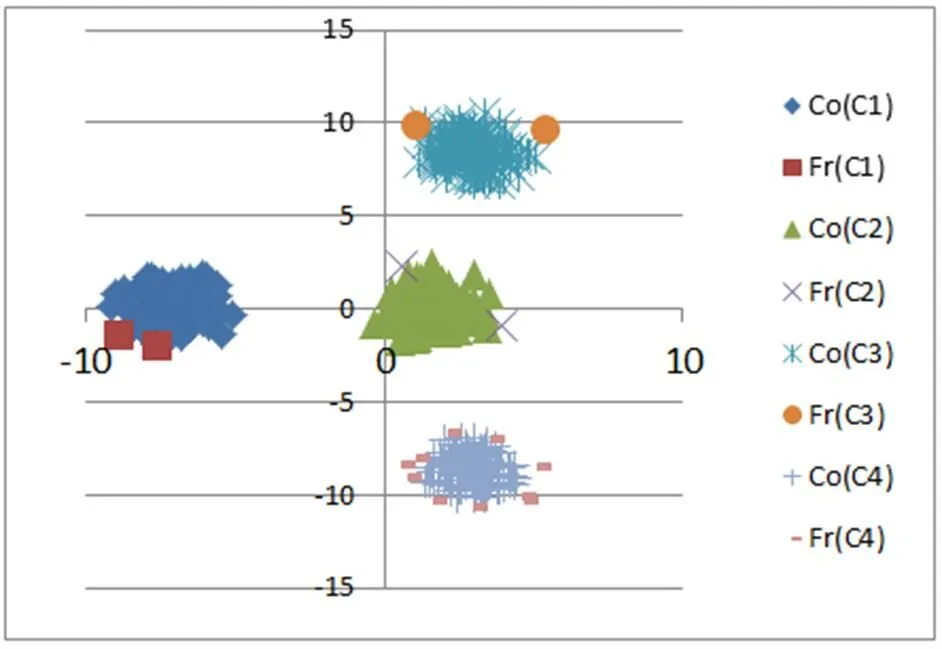
图9 数据集 D3上实验结果

图10 数据集 D4上实验结果
从图7-10可知:在D1 数据集上,文中算法找到了3个类之间的重叠部分,把重叠部分对象分别划分到相应类的边缘域中。数据集D2中的3个类彼此分离没有重叠部分。文中的三支决策聚类方法并没有强制找出类之间的重叠部分,即不存对象同时属于多个类的现象,而是把每个类中离该类中大部分对象较远的对象,划分到类的边缘域中。数据集D3中的4个类彼此分离没有重叠部分。同样,文中的三支决策聚类方法并没有强制找出类之间的重叠部分,即不存对象同时属于多个类的现象,而是把每个类中离该类中大部分对象较远的对象划分到类的边缘域中。在D4 数据集上,文中算法找到了2个类之间的重叠部分,把重叠部分对象分别划分到相应类的边缘域中。同时,两个类中存在少部分对象远离类中的其它对象,文中算法把这些对象也划分到相应类的边缘域中。
通过实验可以验证文中提出的三支决策聚类方法是有效的。文中提出算法不仅能够找出类间的重叠部分,同时还能根据类中对象之间的紧密程度对类中对象做进一步区分,得到更加丰富的信息,便于对聚类结果的进一步分析。
4 三支聚类研究
本文主要阐述并解释了三支决策聚类问题。传统的聚类分析中通常将一个类簇用一个集合来表示,通过两个域来描述一个类簇,是一个典型的二支决策问题,即对象确定属于某个类簇或确定不属于某个类簇。但实际应用中,存在着很多情况是难以给出明确二支决策结果的。受三支决策理论的启发,本文提出用两个集合即三个域来描述一个类簇:核心域中数据对象确定属于该类簇,琐碎域中数据对象确定不属于该类簇,边缘域中数据对象可能属于也可能不属于该类簇。这种表示方法可以更加直观地展示数据对象确定属于或可能属于某个类簇。通过对边界域中数据对象进一步处理,可以更加清晰地了解到其对所属类簇的影响程度。认为关于三支聚类还有以下几方面的关键问题:
(1)三支聚类的表示。通过区间集、决策粗糙集来对三支决策聚类进行表示的相关工作已经取得了一定的进展。接下来,可以考虑通过模糊集、阴影集以及其他的模型来对三支聚类进行表示。针对不同聚类问题,不同的表示方法会得到不同的结果。
(2)三支聚类方法的研究。通过二支决策扩展得到三支决策的方法是非常合理的。但是阈值的设定以及类簇个数的确定对三支决策聚类算法的效率会产生很大的影响。
(3)针对动态数据或不完备数据,如何设计更高效合理的算法也是一个研究重点。
(4)三个域的应用。可以将三支决策聚类算法应用到实际问题中,比如社交网络、网络营销、电子商务、推荐系统等。
[1] XU R. Survey of clustering algorithms [J]. Neural Networks IEEE Transactions on, 2005, 16(3):645 - 678.
[2] Hoppner F, Klawonn F, Kruse R, et al. Fuzzy cluster analysis: methods for classification, Data Analysis and Image Recognition [J]. Journal of the Operational Research Society, 2000, 51(6):769-770.
[3] LINGRAS P, YAN R. Interval clustering using fuzzy and rough set theory[C]// In Proc.2004 IEEE Annual Meeting. Fuzzy Information, Ban, Alberta, 2004: 780-784.
[4] LINGRAS P, WEST C. Interval set clustering of web users with rough k-Means [J]. Journal of Intelligent Information Systems, 2004, 23(1):5-16.
[5] YAO Y Y, Lingras P, Wang R, et al. Interval set cluster analysis: a re-formulation[C]// Rough Sets, Fuzzy Sets, Data Mining and Granular Computing, International Conference, India: Delhi, 2009: 15-18.
[6] CHEN M, MIAO D Q. Interval set clustering [J]. Expert Systems with Applications, 2011, 38(4): 2923-2932.
[7] YAO, Y Y. An outline of a theory of three-way decisions[C]// Rough Sets and Current Trends in Computing,8th International Conference, RSCTC2012 . Berlin Heidelberg : Springer Press , 2012: 1-17.
[8] YAO Y Y. Three-way decisions and cognitive computing [J]. Cognitive Computation, 2016:1-12.
[9] Azam N, Yao J T. Analyzing uncertainties of probabilistic rough set regions with game-theoretic rough sets[J]. International Journal of Approximate Reasoning, 2013, 55(1):142-155.
[10] LIANG D, LIU D. A novel risk decision making based on decision-theoretic rough sets under hesitant fuzzy information [J]. IEEE Transactions on Fuzzy Systems, 2015, 23(2):237-247.
[11] ZHOU B, YAO, LUO J. Cost-sensitive three-way email spam filtering [J]. Journal of Intelligent Information Systems, 2014, 42(1):19-45.
[12] CHEN H, LI T, LUO C, et al. A decision-theoretic rough set approach for dynamic data mining [J]. IEEE Transactions on Fuzzy Systems, 2015, 23(6):1958-1970.
[13] LI Y, ZHANG Z H, CHEN W B, et al. TDUP: an approach to incremental mining of frequent item sets with three-way-decision pattern updating [J]. International Journal of Machine Learning & Cybernetics, 2015:1-13.
[14] ZHANG , ZOU H, CHEN X, et al. Cost-sensitive three-way decisions model based on CCA[M]// Rough Sets and Current Trends in Computing. Springer International Publishing, 2014:172-180.
[15] LI H X, ZHOU X Z. Risk decision making based on decision-theoretic Rough Set: A three-way view decision model [J]. International Journal of Computational Intelligence Systems, 2013, 4(1):1-11.
[16] YU H, LIU Z G, WANG G Y. An automatic method to determine the number of clusters using decision-theoretic rough set [J]. International Journal of Approximate Reasoning, 2014, 55(1):101-115.
[17] YU H, WANG Y. Three-way decisions method for overlapping clustering[M]// Rough Sets and Current Trends in Computing. Springer Berlin Heidelberg, 2012:277-286.
[18] YU H, ZHANG C, HU F. An incremental clustering approach based on three-way decisions [M]// Rough Sets and Current Trends in Computing. 2014:152-159.
[19] YU H, SU T, ZENG X H. A three-way decisions clustering algorithm for incomplete data [M]// Rough Sets and Knowledge Technology. Springer International Publishing, 2014:765-776.
[20] YU H, JIAO P, WANG G Y, et al. Categorizing overlapping regions in clustering analysis using three-way decisions[C]//IEEE/WIC/ACM International Joint Conferences on Web Intelligence. 2014:350-357.
[21] YU H, ZHANG C, WANG G Y. A tree-based incremental overlapping clustering method using the three-way decision theory [J]. Knowledge-Based Systems, 2016, 91:189-20
Three-way Cluster Analysis
YU Hong*
(Chongqing Key Laboratory of Computational Intelligence, Chongqing University of Posts and Telecommunications, Chongqing 400065, China)
This paper proposes a new clustering strategy, named three-way decision clustering, or simply "three-way cluster" for short, which is inspired by the theory of three-way decisions. In the three-way cluster analysis, a cluster is represented by two sets instead of a single set, and the two sets called the core region and fringe region. Objects in the core region are typical elements of the cluster. Objects in the fringe region are fringe elements of the cluster, and they might or might not belong to the cluster. The new strategy has the ability to deal with the conventional hard or soft clustering. Besides, this paper proposes an evaluation-based three-way decision clustering model and illustrates an approach of three-way clustering based on k-means as an instance. The paper also reviews recent three-way clustering studies and points out the future research directions.
clustering; three-way decision; uncertainty; hard clustering; soft clustering
1672-9129(2016)01-00032-06
TP391
A
2016-07-05;
2016-07-21。
三支决策聚类理论模型与方法研究(61379114)。
于洪(1972-),女,重庆,教授,博士,主要研究方向:粗糙集、三支决策、智能信息处理、Web智能、数据挖掘。
(*通信作者电子邮箱:yuhongcq@aliyun.com)
- 数码设计的其它文章
- 基于邻域的名词型数据分类方法

