热声系统高温段的漏热分析与防护结构的优化设计
李 娟 周 刚 李 青
(1中国科学院理化技术研究所航天低温推进剂技术国家重点实验室 北京 100190)(2中国科学院大学 北京 100049)
热声系统高温段的漏热分析与防护结构的优化设计
李 娟1,2周 刚1李 青1
(1中国科学院理化技术研究所航天低温推进剂技术国家重点实验室 北京 100190)(2中国科学院大学 北京 100049)
对热声系统高温段的漏热进行理论分析,建立高温段真空防护结构的物理模型,并基于fluent中S2S模型,对模型进行了稳态数值模拟,得到了辐射散热量、导热量、外表面的热流量随加热温度的变化,以及辐射和导热占总漏热量的比值;在此基础上,对防护结构进行优化,提出防护结构2,对比分析了两种热防护结构的防漏热效果。结果表明,真空防护结构会有效的减少系统的漏热,增大系统的热声转换效率,且优化后的结构2较结构1更能有效的减少系统漏热。
热声 高温漏热 真空 结构设计
1 引 言

关于热声系统漏热的研究很少,对于高温段的漏热研究,李山峰[1]通过实验的手段,测量得到在发动机热端温度550 ℃以上时,通过保温层的漏热量达到200 W以上,从而提出,通过减小回热器以及热缓冲管管壁的厚度降低导热损失,减小热端换热器以及次水冷器表面的黑度来降低辐射换热损失,并改进保温措施以减少漏热。另外与一般的流动换热不同,热声系统内是交变流动换热。在交变流动换热的研究中,Dean, smith等[2]对管内交变流动传热进行实验研究,引入复努塞尔数,获得每一阶热流密度和温差以及两者间的相位角,进而求得每一阶的复换热系数以及复努塞尔数。然而周期换热的情况未给出,使得其研究结果无法推广应用于一般情况的交变流动传热计算。Bouvier等[3]针对圆管内交变流动传热进行了实验研究,采用反传热的方法,通过测量壁面内的温度或是流体的温度,推导得到交界面处的热流密度和温度以及无量纲换热系数,但是其测量方法比较困难,精度难以保证。本文主要对高温段的漏热进行理论分析,建立了高温段真空防护结构的模型,并通过静态模拟的方式对该模型的防漏热效果进行模拟研究;在此基础上对热防护结构进行优化,对比分析了两种结构的防漏热效果。
2 理论分析
回热器是热声系统的核心部件,其两端的温度差是热声转换的必要条件。装置中的回热器和热缓冲管固定下来后,维持回热器固定温差值所需要的理想加热量是不变的。如图1所示,行波热声发动机环形圈中,通过加热器对热声热机进行加热并保持回热器两端有着合适的温度差。因此加热器、回热器以及缓冲管段的温度较系统其它位置的温度高约50—200 K,温度较高,对流和辐射漏热较大。在不采用减少漏热措施的情况下,高温段的漏热,主要包括自然对流换热E对流和辐射漏热E辐射(包括对外界环境的辐射漏热和对冷端换热器的辐射漏热)。本次主要针对高温段对外界环境的漏热进行研究,因此,计算中忽略对冷端换热器的辐射漏热,以下所指辐射散热即为对外界环境的辐射散热,总漏热指对外界环境的辐射散热与自然对流散热之和。按自然对流换热系数6W/m2K,高温段面积为9.24×10-3mm2,温度为650K对自然对流换热和辐射漏热量进行计算:
E对流=hAΔt=6×9.24×10-3×
(650-300)W=19.4W
(1)
9.24×10-3×(6504-3004)=35.7 W
(2)
式中:h为自然对流传热系数, W/m2K;A为高温段的表面面积,m2;ε为不锈钢面的发射率;σ为黑体辐射常数,其值为5.67×10-8W/(m2·K4)。

图1 热声发动机环形圈示意图Fig.1 Schematic diagram of annular ring
可以看出,当温度为650K,加热量为280W时,高温段总热损失为55.1W,总漏热占系统总加热量的19.2%,对流换热和对环境辐射散热占加热量较大的比值,严重影响热声转换效率。另外,随着陶瓷加热器温度的升高,根据上式中辐射力E和对流散热量与温度T的关系,温度升高时,外表面的辐射散热量和对流换热量会进一步增大,高温段的热损失会进一步增大。
可见,若不采取减少漏热措施的情况下,系统的自然对流换热和辐射漏热均较高,严重影响发动机系统的热声转换效率。因此,应该对系统的高温段(包括回热器、加热器以及热缓冲管)进行绝热保温,以减少向外界的漏热损失。一般的热声系统中,高温段外壁面采用真空夹层以减少对外界环境的漏热,如图2所示;抽真空以后,真空度可以达到1×10-5Pa。一方面,它可以缓解由于加热器加热引起的管体膨胀可能导致的微小变形,另一方面,可以有效避免夹层内部空气的传导和对流所造成的热损失。

图2 真空腔结构示意图(结构1)Fig.2 Schematic diagram of vacuum cavity (structure 1)
对图2所示的真空腔热防护结构的散热进行分析,上述结构中,加热器的热量传导至真空腔内表面,真空腔内表面的热量一部分通过连接板径向传导至真空腔外表面,一部分通过热辐射进行传热,而系统外表面的散热方式主要是辐射散热和自然对流换热。通过数值模拟的方式对结构1的散热进行模拟研究,
3 数值模拟
3.1 模型选择及边界条件设置
其物理模型如图2所示,采用ICEM进行网格划分,网格质量为0.38;对于模型中的辐射漏热,fluent中主要有5中辐射模型:DTRM模型、P1模型、Rossland模型、Do模型以及S2S模型。
DTRM的主要思想是用单一的辐射射线代替从辐射表面沿某个立体角的所有辐射效应[4];模型的计算精度主要由跟踪射线的数目和计算网格的疏密程度决定;对于大数目的射线问题,非常耗费CPU时间。
P1辐射模型是P-N模型中最简单的类型。P-1模型的主要出发点是把辐射强度方程展开成为正交的球谐函数,对于光学深度比较大(如燃烧应用中),表现非常好。
ROSSLAND模型不计算介质辐射强度的输运方程,而是在P1模型基础上引入与温度成3次方的传热系数来计算辐射传热量,相对于P1模型计算较快,推荐用于光学深度大于3的情况下。
DO模型是从有限个立体角发出的传播方程出发进行求解,将立体角离散化,求解有限个立体角发射出的辐射方程,通过求解各立体角内的辐射运输方程获得辐射强度分布,积分获得辐射热源。
S2S辐射模型非常适用于封闭空间中没有介质的辐射问题,通过设定和计算角系数文件来计算辐射量,从而可以不涉及到辐射介质,因此对于计算真空辐射具有良好的精度。
对比以上辐射模型的使用情况,本文主要是真空辐射,因此采用S2S辐射模型,边界条件设为温度边界条件,模型两端为冷端换热器,因此温度设置为300 K,模型中加热器的温度,根据实验获得,如表1所示。
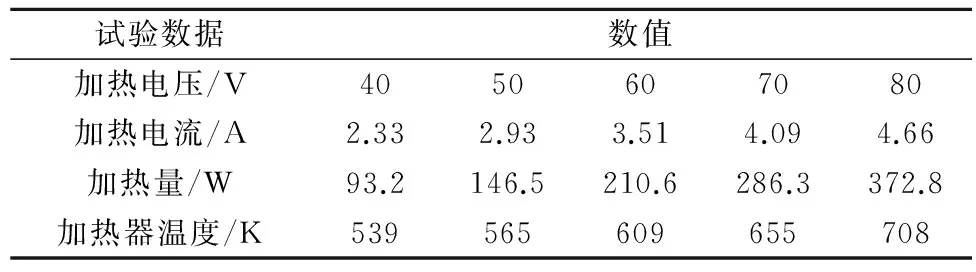
表1 加热器的加热温度与加热量对照表Table 1 Heating temperature and heating quantity of heater
系统主要的气体工质为高压氦气,主要的固体工质不锈钢板和陶瓷加热器,两者的物性参数如表2所示。

表2 主要工质材料的热物性Table 2 Thermal properties of main working materials
3.2 模拟结果及分析
模拟可得上述模型中,真空腔内的辐射散热量、不锈钢支撑的导热量以及系统外表面的温度分布。
图3为系统真空腔内辐射散热量和连接板的导热量随加热器温度的变化,很显然辐射量和导热量均随着加热器温度的升高而升高,辐射散热量由5.2 W上升为16.9 W,导热量由8.7 W上升为12.8 W;这是因为,随着加热器温度的升高,真空腔内表面和系统外表面的温度均随之升高,表面温度的升高必然会导致散热量的增加。由图4辐射量和导热量占总散热量的比值随加热器温度的变化。还可以看出,随着加热器温度的升高,导热量的增长幅度较辐射量的增长较为缓慢,这是因为辐射量与温度成4次方的关系,而导热量是一次方的关系,因此辐射量随温度的变化较为明显。图5、6分别为加热器温度为708 K时,真空腔外表面和内表面的温度分布,在真空腔外表面,温度分布为两端高,中间低,内表面的温度分布则相反,因此可以看出,连接板的热传导在热量传递中占很大比值。另外,温度为650 K时,系统总漏热量为30 W,与不加防护结构的总漏热量55.1 W相比,可有效的减少漏热83.67%。

图3 辐射量和导热量随加热器温度的变化Fig.3 Radiation and heat conduction vs heating temperature

图4 辐射量和导热量的比值随加热器温度的变化Fig.4 Ratio of radiation and heat conduction vs heating temperature

图5 真空腔外表面的温度分布图Fig.5 Temperature distribution on outer surface of vacuum cavity

图6 真空腔内表面的温度分布Fig.6 Temperature distribution on inner surface of vacuum cavity
3.3 热防护结构的优化设计
为了进一步减小辐射漏热,可在真空腔中加一层辐射屏,在稳定条件下,
q1,3=εs(Eb1-Eb3)
(3)
q3,2=εs(Eb3-Eb2)
(4)
式中:q1,3,q3,2分别为真空腔表面1对遮热板和遮热板对表面2的辐射传热热流密度,且两个系统的发射率相同,均为:
(5)
在热稳态条件下,q1,3=q3,2=q1,2。将式(3)和式(4)相加可得,
(6)
与未加辐射屏时的辐射传热相比,其辐射传热量减小了一半。另外为使削弱辐射传热的效果更为明显,可采用发射率较低的金属薄板作为遮热板或多层遮热板。
根据以上分析,建立热防护结构优化后(结构2)的模型,如图7所示。结构2在结构1的基础上,为了减少真空腔内的辐射散热,在真空腔内部焊接遮热板。此时真空腔内表面的热量辐射至遮热板,再经遮热板辐射至真空腔外表面。由于遮热板的温度高于连接板的温度,因此遮热板的热量一部分还会通过轴向导热传至连接板,并进一步由连接板传导至真空腔外表面以及系统外表面。因此,结构2系统的辐射散热量是减小的,但导热量在一定程度上是增加的,为了减少结构2的轴向导热散热量,研究对遮热板进行间断处理。对结构2的散热进行数值模拟研究。

图7 优化后的结构示意图(结构2)Fig.7 Schematic diagram of optimized structure (structure 2)
对结构2的数值模拟研究中,采用与结构1中相同的边界条件与辐射模型。其模拟结果如图8—11所示,分别为两种结构下辐射量、导热量、系统外表面热流量以及外表面温度随加热器温度的变化。首先很显然,在相同的加热器温度下,结构1的辐射散热量要高于结构2,但其导热量却低于结构2 的导热量,这些在上述的理论分析中都是可以直接得到的。经过模拟分析,还可以看出,在相同的加热器温度下,结构1中系统外表面的热流量和温度均要高于结构2,由此可见,虽然结构2中遮热板的存在增加了系统的导热散热量,但是这部分的散热量在整个系统散热量中占很小的比例,例如,当加热器温度为609K时,结构1的导热量为10.4W,结构2 的导热量为10.7W,仅仅增加了0.4W,但其辐射散热量却由此平均减少了2.5W,且结构2的外表面温度明显低于结构

图8 两种结构下辐射量随加热温度的变化Fig.8 Radiation vs heating temperature for two different structures

图9 两种结构下导热量随加热温度的变化Fig.9 Heat conduction vs heating temperature for two different structures
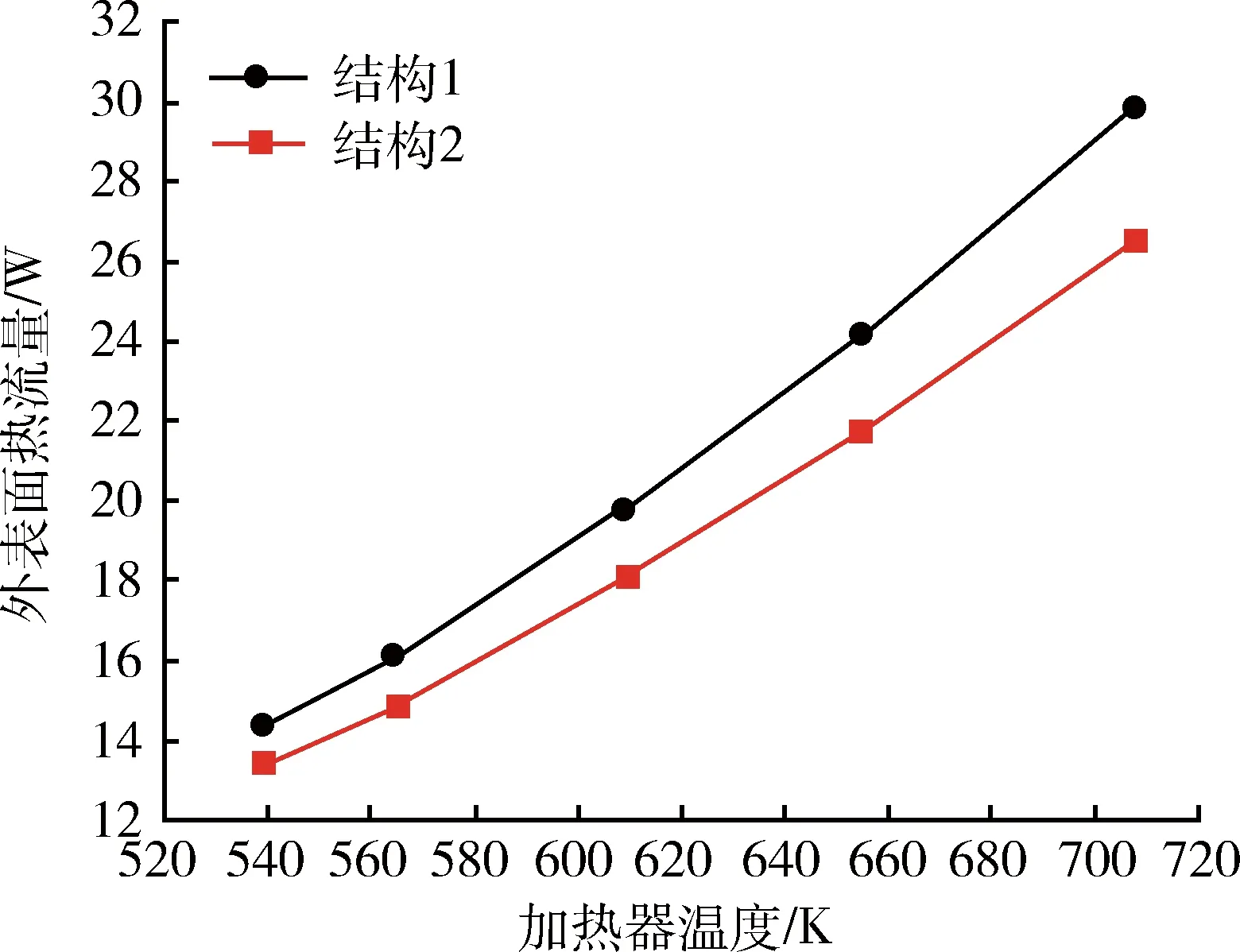
图10 两种结构下外表面热流量随加热温度的变化Fig.10 Heat flux vs heating temperature for two different structure

图11 两种结构下外表面平均温度随加热温度的变化Fig.11 Average temperature vs heating temperature for two different structures
1,外表面温度的降低也会进一步减小对流散热;因此结构2的总漏热要小于结构1的漏热,即结构2要优于结构1。
4 结束语
对热声系统的高温段的漏热进行理论和数值模拟研究,分析了两种结构的防漏热效果。结果表明,由于漏热的存在,导致系统漏热约55 W,占系统总加热量的19.2%以上,且加热的温度越高,漏热越大;真空防护结构会有效的减少系统的漏热,增大系统的热声转换效率;优化后的结构2较结构1更能有效的减少系统漏热,这些都为高温段真空防护结构的设计提供了指导方向;然而本文主要进行稳态漏热的模拟研究,且并未考虑回热器丝网的导热,因此存在一定误差。在下一步的工作中,会进一步进行交变流动漏热的研究。
1 李山峰.行波热声发动机、制冷机及其耦合规律研究[D].北京:中国科学院理化技术研究所, 2009.
Li Shanfeng.Research on traveling wave thermoacoustic engine, refrigerator and its coupling law [D].Beijing:Institute of physics and chemistry,Chinese Academy of Sciences,2009.
2 Dean C E.Establishing Baseline data for an Experimental Paratus that Measures Heat Transfer Under Conditions of Ocillating Pressure and Flow[D].Massachusetts Institute of Techonology.1993.
3 Bouvier P,Stouffs P,Bardon J P.Experimental study of heat transfer in oscillating flow[J].International Journal of Heat & Mass Transfer,2005,48(12):2473-2482.
4 温 正,石良辰,任毅如.等.FLUENT流体计算应用教程[M] .北京:清华大学出版社,2009.
Wen Zheng,Shi Liangchen,Ren Yiru.FLUENT fluid computing applications tutorial[M].Beijing:Tsinghua University Press,2009.
Heat leakage analysis and optimum design of high temperature section of thermoacoustic system
Li Juan1,2Zhou Gang1Li Qing1
(1State Key Laboratory of Technologies in Space Cryogenic Propellants ,Technical Institute of Physics and Chemistry Chinese Academy of Sciences, Beijing 100190, China)(2University of Chinese Academy of Sciences, Beijing 100049, China)
Theoretical analysis of heat leakage has been made in the high temperature section of the thermoacoustic system. Physical model of the vacuum cavity structure is established, the steady-state numerical simulation is carried out basing on S2S model. The amount of radiation, heat conduction and heat flux of the external surface with the change of the heating temperature, and the ratio of radiation and heat conduction to the total leakage rate were obtained. On this basis, an optimized structure, structure 2 is proposed. And thermal protection effect is compared between two different structures. The results show that the vacuum protection structure can effectively reduce the heat leakage of the system, increase the efficiency of the system, and the optimized structure 2 is more effective than the 1.
thermoacoustic;high temperature;vacuum cavity;structure design
2016-04-21;
2016-06-01
李 娟,女,24岁,硕士研究生。
TB65
A
1000-6516(2016)03-0030-05

