液氮汽蚀实验中低温热电偶的标定及误差分析

谢黄骏 朱佳凯 徐 璐 陈建业 张小斌*

(1浙江大学制冷与低温研究所 杭州 310027) (2浙江省制冷与低温技术重点实验室 杭州 310027)

液氮汽蚀实验中低温热电偶的标定及误差分析

谢黄骏1,2朱佳凯1,2徐 璐1,2陈建业1,2张小斌1,2*

(1浙江大学制冷与低温研究所 杭州 310027) (2浙江省制冷与低温技术重点实验室 杭州 310027)

提出并验证了一种方便、快捷的获得77—90 K之间稳定温度点的方法，并基于该方法对应用于液氮汽蚀实验中温度测量的热电偶进行了标定。对标定后热电偶的测温结果进行了详细的不确定度分析，该分析方法旨在结合标定与使用时的各种条件对测量结果的影响，得出应用该热电偶进行每一次测温时所得结果的综合不确定度。分析结果表明，该方法标定所得的热电偶具有良好的测温精度，满足液氮汽蚀实验的测温需求；Keithley2700在测量热电势时的量程误差分量是对标定热电偶测温精度影响最大的部分。

低温 热电偶 标定 不确定度分析 液氮

1 引 言

各类低温热电偶由于其简单、无需激励电流及反应快等优点，广泛应用于低温流体流动和传热实验过程的温度测量。而在涉及的77—90 K温区，T型热电偶(铜-康铜热电偶)具备较好的性能稳定性及较高的灵敏度[1]，往往被研究者优先采用。若经过适当的标定，热电偶测量不确定度可以小于0.5 K，如NASA报道的在液氮文氏管汽蚀实验中，T型热电偶测温精度达±0.2 K[2]，但每次实验前需要对热电偶进行标定。一般热电偶标定方式是以冰点为参考点，利用液氮、沸水、冰点3点温度测得相应电势差，进行二次拟合得到热电偶的测温曲线。通过这种方法得到的标定曲线存在以下问题：由于二次拟合时需要计算3个参量，利用3点进行二次拟合固然可以得出二次曲线的表达式，却不能得到基于该曲线计算得到温度可靠性的任何结论，因为二次拟合时拟合点与曲线的偏差程度δy：

(1)

式中：A、B、C为通过3点计算而得的二次曲线的系数；γ=N-3=0为自由度，此时3点正好在拟合曲线上，出现0/0的情形。

另外，液氮(78 K)、冰点(273 K)、沸水(373 K)3点温度跨度过大，若实验过程温度变化范围在77—90 K之间，则温度测量结果准确性不高往往不能满足要求。因此，若只需要在小温度范围内使用的热电偶，在该温区内进行标定可以获得更高的测温精度，关键是获得温区内稳定的标定温度点。经过多次实验发现，液氮、液氧按不同比例混合时能得到77—90 K温度范围内稳定性很好的不同温度点本文对这种热电偶的标定方式进行了介绍，并且详细地分析最终获得的标定公式用以进行温度测量时的不确定度。

2 标定过程

热电偶标定装置如图1所示。冰点槽使用具有真空隔层的保温桶制成，里面放置均匀的冰水混合物，作为参考端温度，温度值由标准铂电阻(PT100，精度0.1 K)温度计测定。热电偶一端用热缩管包裹好浸没在冰水混合物中，避免和冰块直接接触；低温液体放置在高密度泡沫盒制成的敞口容器中，其温度也由标定好的铂电阻测量。

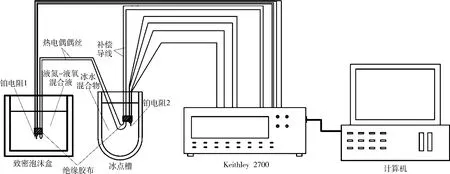
图1 热电偶标定装置示意图Fig.1 Schematic diagram of thermocouple calibration installations

数据采集使用Keithley2700数据采集仪+Module7708板卡进行四线制铂电阻阻值读取及电势差采集，采用GPIB/USB数据线连接计算机进行数据显示和储存；采用LabVIEW编程，对Keithley2700的采集过程进行控制。

为保证标准铂电阻温度计与标定温度计测到相同温度，标定过程首先将两者两个测温端用绝缘胶布绑在一起。低温容器首先盛放足够纯液氮，再按次加入适量液氧，监视铂电阻温度计温度和热电偶电势差，稳定后获得一个温度点。继续加入适量液氧可获得更多稳定点。

2 测量数据

在实验中，低温容器温度在80 s时长内基本保持不变认为达到了稳定，如图2所示，取其平均值作为标定温度，同样的，取该时间内热电偶平均热电势为测量电势。按照不同液氮液氧混合比例，得到了5个温度点(包含总共397个数据点)，其中，第1个点和第5个点分别是纯液氮、液氧时的数据。图2a—图2e分别为铂电阻测得的5个在监测时间内测得的温度及热电偶电势差。对数据进行分析发现，5组温度数据的极差分别为：0.03 K、0.03 K、0.03 K、0.04 K、0.02 K。对每一组数据，取其3倍样本标准差(σ)作为温度波动性的表征，可得3σ<0.1 K，具体的计算将在下面说明。图3给出了实验过程冰水混合中热电偶参考端温度测量结果。由图可见，液氮-液氧不同比例混合得到的混合液拥有非常好的温度稳定性。

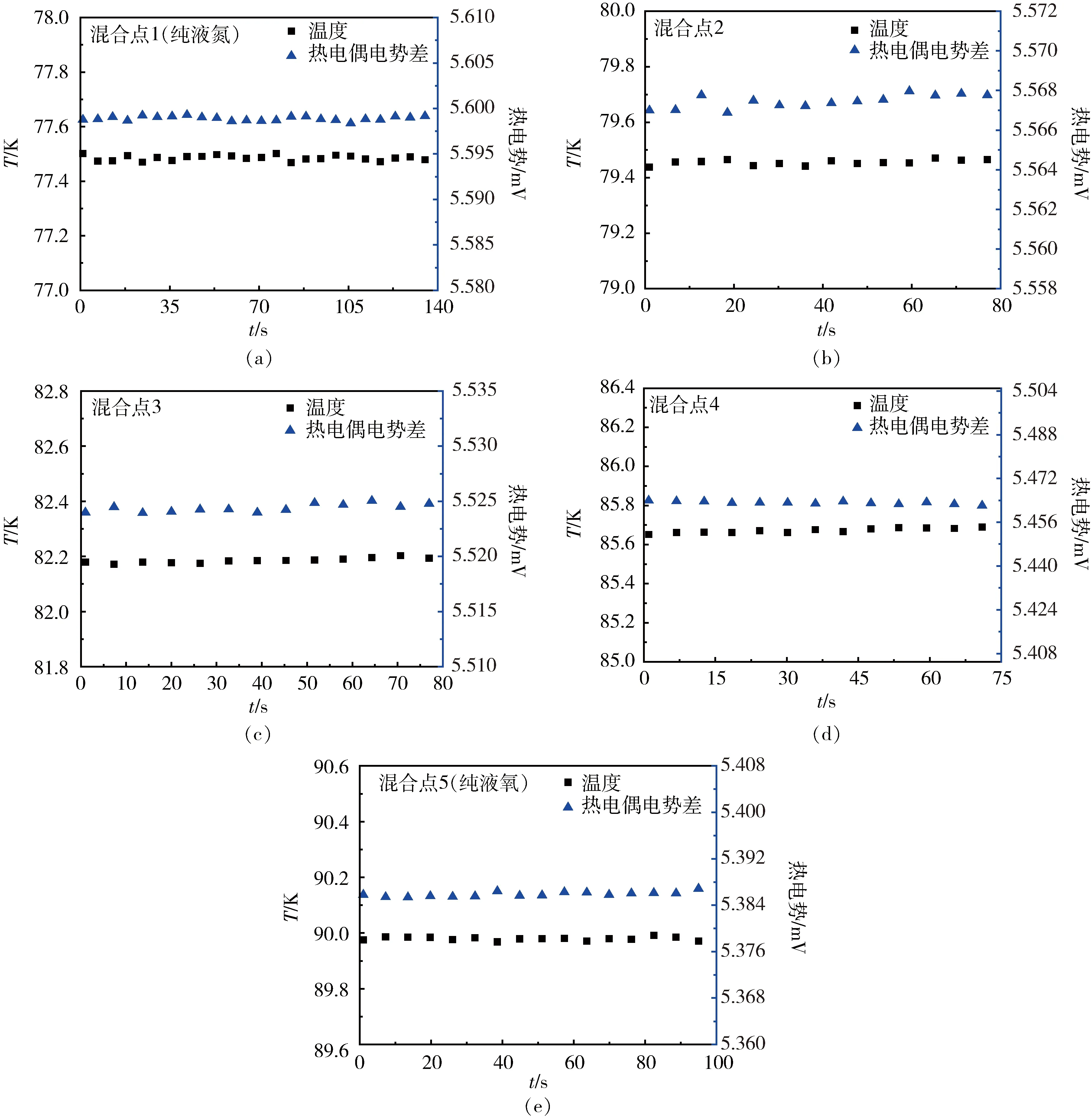
图2 液氮-液氧混合所得溶液温度Fig.2 Temperature of mixed solution of liquid nitrogen and liquid oxygen

3 数据分析

表1给出了得到的5组温度-电势差平均值。利用最小二乘法进行拟合得到自变量为电势(e)的二阶多项式，多项式系数a，b，c的值分别为：a=-26.278 7，b=230.073 0，c=-386.892 1。

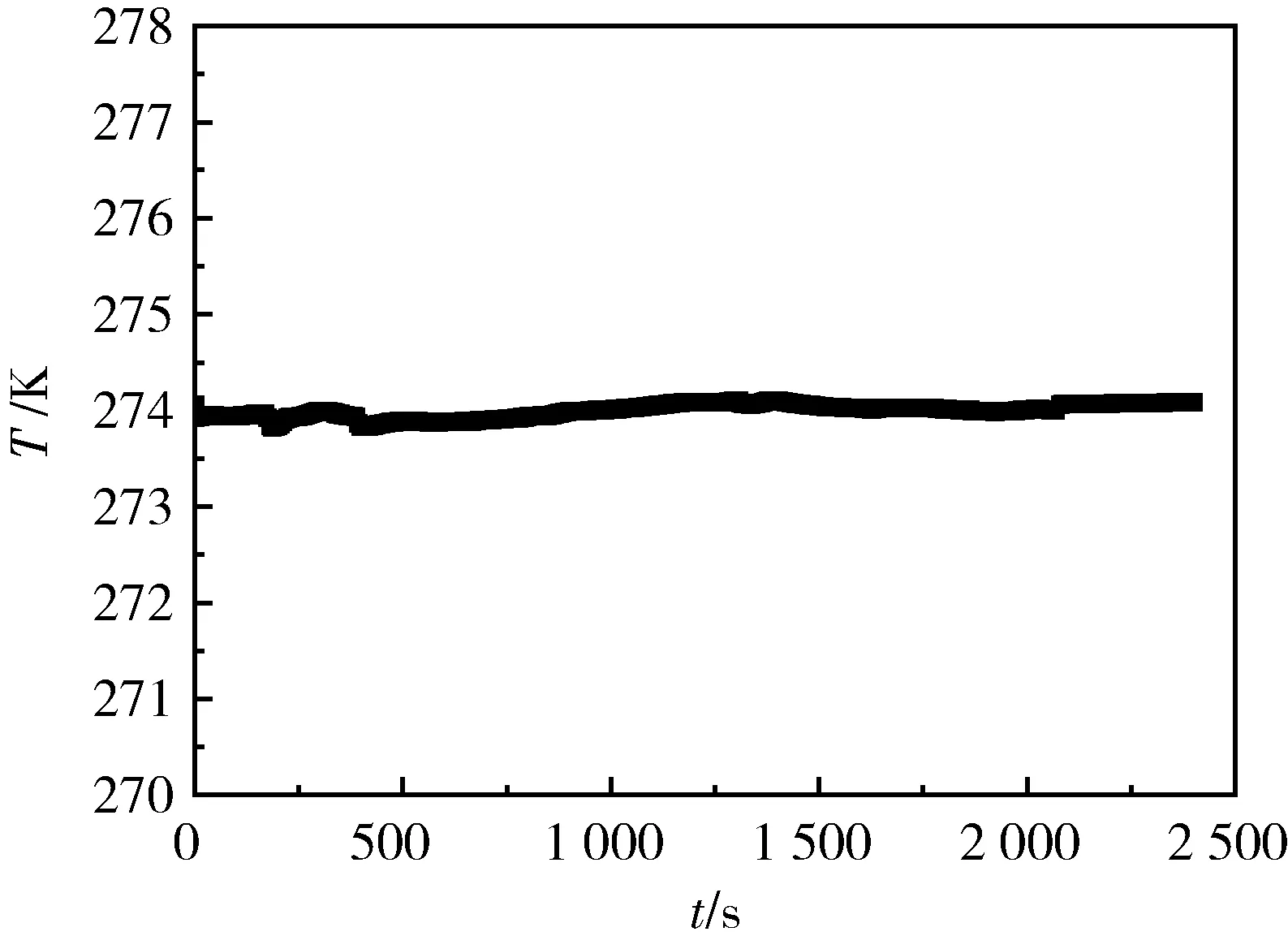
图3 冰水混合物参考点温度Fig.3 Temperature of reference point in ice-water mixture

表1 液氧液氮混合物中得到的5组平均温度和电势差Table 1 5 groups of average temperature and thermal-emf values

由此得到该热电偶在77.49—89.98 K温度区间内的温度-电势差关系式：

T=-26.278 7e2+230.073 0e-386.892 1

(2)

式中：温度单位为K，电势差单位为mV。将式(2)作图便得到图4。

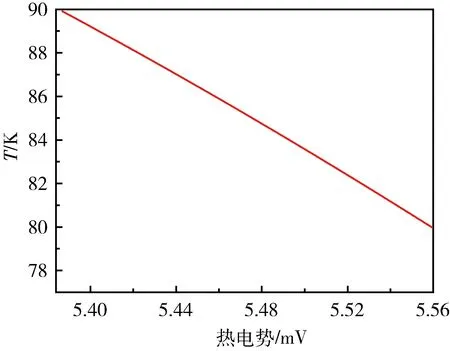
图4 热电偶温度和热电势拟合曲线Fig.4 Fitting curve of temperature and thermo-emf for thermocouple

4 误差分析

标定过程中标定点温度、电势差以及参考端温度的值都使用稳定之后一系列测量数据的平均值作为拟合计算用值。热电偶标定过程中，温度总不确定度由5个相互独立的不确定度综合而得，其中3个与标定时引入的不确定度相关，2个与实际使用条件相关，分别进行计算：

4.1 由室温参考端温度不确定度(σr)引起的低温端温度不确定度(σc)

热电偶两端由于温度差引起的温差电势，可由式(3)计算：

(3)

式中：下标r表示参考端(≈273 K)，下标c表示测量端(77—90 K)。因此，当δTr很小时可将由参考端温度波动引起的电势差转换为等价的低温端温度波动引起的电势差δTc：

ΔE(Tc，Tr±δTr)=aTrδTr

(4)

式中：aT为温度T时的塞贝克系数。由文献[5]查得，273 K时aTr=38.816 μV/K，77 K附近aTc=16.280 μV/K。于是：

(5)

对物理量φ进行n次测量取平均之后平均值的不确定度为：

(6)

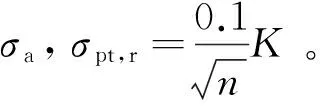
使用Keithley2700对铂电阻阻值进行测量时，所得结果会有一个不确定度σR，将其转化值铂电阻温度测值的不确定度σy：

(7)

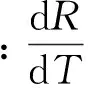
本次实验中，测量了n=397个参考端的温度数据，取平均值得参考端温度为274.00 K，将数据代入式(3)—(7)，可得σc=0.050 K。

4.2 对标定点的温度、电势测量都存在误差，造成使用该拟合公式测温时的不确定度(σm)

基于测量得到的5组稳定温度、电势数据，采用最小二乘法得到二次拟合曲线：T=ae2+be+c，令

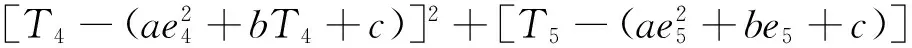
(8)

求解方程组：

(9)

可得a、b、c的值，由此也可以发现a、b、c分别都是(e1、e2、e3、e4、e5、T1、T2、T3、T4、T5)的函数。

将第k个标定点的温度数据代入式(6)得温度不确定度为，同样将第k个标定点的电势数据代入式(6)得到σek。

由误差传递公式，第k个标定点的电势、温度不确定度传递至最终的测温结果的不确定度为：

(10)

可以看到，σm,k是一个与实际使用时测得的电势有关的量。

在求解a、b、c对Tk、ek的偏导时，将不可避免地使用符号求解再将数值代入计算，事实上，对其进行符号求解是一件非常繁琐且容易出错的工作，实际操作时使用数学软件MATLAB编程进行符号求解并将数值代入求得结果。

由5个标定点的温度、电势测值的不确定度造成的测温结果的不确定度为：

(11)

4.3 若对温度、电势的测量无误差，拟合曲线偏离真值引入的误差(σd)

(12)

式中：ek、Tk分别为第k个点电势和温度，γ是这个该计算阶段的自由度，对于本次实验在该阶段的计算，γ=N-3=2。

将5个标定点数据及拟合公式代入式(10)得到σS=0.057 K。

4.4 热电偶电势测不确定度造成的温度不确定度(σp)

假设设备对于电势差的读取时的不确定度为σe，根据误差传递公式

(13)

使用该热电偶时冰点槽温度的设置温度存在误差(σf)，造成测温结果的不确定度(σq)，与4.1节中的分析相似

(14)

其中冰点槽设置温度的不确定度σf由使用时冰点槽的具体情况而定。

综上，由该标定好的热电偶进行一次温度实验所得结果的不确度的综合为：

(15)

对温度的测量结果表示为：T=T(e)±σT

其中T(e)是测得电势差之后利用拟合公式计算而得的温度。

根据上述不确定度分析，对测量结果进行分析，得到冰点槽温度为274.00 K。使用标定好的热电偶对一液氮-液氧混合液进行了温度测量，使用Keithley2700记录热电偶电势及铂电阻阻值，得到稳定后的电势读数为5.493 7 mV，冰点槽温度不确定度为0.050 K，将数据代入式(10)、式(11)、式(13)—式(15)，结合已经得出的σc、σd，计算得到这次测温所得结果的不确定度为0.24 K，同时由式(1)计算得到其测得温度为83.95 K，于是该次测温实验所得结果表示为：T=(83.85±0.24)K。同时由铂电阻测得的温度为(84.05±0.1)K，(84.05±0.1)K-83.95 K∈[0 K，0.2 K]∈[-0.24 K，0.24 K]。可以发现，该标定方法标定得到的热电偶在使用温度范围内对温度进行测量得到了良好的精度，满足液氮汽蚀实验的测温需求。

实验发现，对拟合公式的不确定度影响最大的是Keithley2700在对电势进行测量时的量程误差，由于其最小档位是100 mV档，而测量的电势都在6 mV以下，使得量程误差的影响很显著，若是能将量程误差降低50%，则上述测温结果的精度能达到±0.15 K以内。

5 结 论

验证了一种简单标定77—90 K温区热电偶的方法，考虑了各相关因素影响，对拟合二次曲线进行了误差分析，验证了拟合公式有良好的精确度，为液氮实验中温度测量打下基础。

严格地说，在没有确定使用条件之前，不能明确地给出热电偶测温的不确定度。而当使用条件已知，即使用时的测量仪表、参考端不确定性已知后，可以给出其在使用范围内的最大不确定度或叫最低精度(出现在测量纯液氮温度时)，即利用电势差达到使用上限时结合仪表、参考端精度计算所得的不确定度，对于和上述使用该热电偶进行测温实验时一样的使用条件，本次实验所标定的热电偶的最低精度为±0.24 K。

1 陈良，侯予，习兰. 铜-康铜热电偶的标定与误差分析[J]. 低温工程，2008(6)：18-23.

2 Hord J，Anderson L M，Hall W J. Cavitation in liquid cryogens(1)[J]. Venturi，1972.

3 John R Taylor著，王中宇，等译. 误差分析导论-物理测量中的不确定度(第二版)[M].北京：高等教育出版社，2015：171-194.

4 周昌文. 低温热电偶[J]. 低温与超导，1980(4)：4.

5 卢锦宝译，金元生校.测量热电偶应用手册[M].北京：机械工业出版社，1983：336-338.

6 胡幼明，Paul Luyeye Luymas，王惠龄. NiCr-CuFe低温热电偶的实验室分度方法[J]. 低温工程，1997(4)：23-26.

7 赵东方.液氮文氏管汽蚀动态特性可视化实验研究[D]. 杭州：浙江大学，2016：13-42.

8 甘智华，张小斌，王博.制冷与低温测试技术[M]. 杭州：浙江大学出版社，2011.

Calibration and error analysis of cryogenic thermocouple used in liquid nitrogen cavitation experiment

Xie Huangjun1,2Zhu Jiakai1,2Xu Lu1,2Chen Jianye1,2Zhang Xiaobin1,2*

(1Institute of Refrigeration and Cryogenics，Zhejiang University，Hangzhou 310027，China) (2Key Laboratory of Refrigeration and Cryogenic Technology of Zhejiang Province，Hangzhou 310027，China)

A convenient and efficient method to obtain the stable temperature points between 77-90 K was proposed and verified.A thermocouple used in liquid nitrogen cavitation experiment for temperature measurement was calibrated based on this method. Detailed uncertainty analysis，which aims to combine the influence of various conditions on the measurement results and obtains the overall uncertainty of measurement result，was applied in the temperature measurement result of that calibrated thermocouple. Analysis result shows that the thermocouple calibrated by that method has a good temperature measurement precision，and meets the requirement of temperature measurement in liquid nitrogen cavitation experiment. The uncertainty of full scale range of Keithley 2700 in thermo-emf measurement accounts for the largest proportion of the overall uncertainty.

cryogenic；thermocouple；calibration；uncertainty analysis；liquid nitrogen

2016-05-26；

2016-06-30

国家自然科学基金(No.51276157)、浙江省杰出青年基金(No.R15E060001)。

谢黄骏，男，22岁，硕士研究生。

张小斌，男，40岁，博士、博士生导师、教授。

TB663

A

1000-6516(2016)04-0016-05