浅化波浪层流边界层流速分布特性的数值分析

李诚，张弛 *，隋倜倜

（1.河海大学海岸灾害及防护教育部重点实验室，江苏南京210098；2.河海大学港口海岸与近海工程学院，江苏南京210098）



浅化波浪层流边界层流速分布特性的数值分析

李诚1，2，张弛1，2 *，隋倜倜1，2

（1.河海大学海岸灾害及防护教育部重点实验室，江苏南京210098；2.河海大学港口海岸与近海工程学院，江苏南京210098）

摘要：建立了同时考虑波致雷诺应力和时均水平压强梯度影响的二阶波浪边界层数学模型，模型计算得到的浅化波浪层流边界层内瞬时流速剖面、振荡速度幅值和时均流速剖面均与水槽实验数据吻合较好，在此基础上探讨了浅化波浪边界层流速分布特性及其影响机制。随着波浪的浅化变形，边界层内时均流速剖面“底部向岸、上部离岸”的变化特征越来越明显。这是二阶对流项引起的波致雷诺应力和离岸回流引起的时均水平压强梯度共同作用的结果，在床面附近由波致雷诺应力占主导作用并趋于引起向岸流动，在上部区域由时均水平压强梯度占主导作用并趋于引起离岸流动。

关键词：波浪浅化；底部边界层；时均流速；数值模拟

1　引言

近岸波浪水质点的振荡运动受到底床摩阻的影响，在床面上方形成毫米至厘米级的薄层，即波浪边界层。波浪边界层内存在较大的流速梯度并催生床面剪切应力，是近岸泥沙运动的重要驱动力。研究波浪边界层内的水流分布特征和床面剪切应力变化对认识海岸泥沙运动和地形演变具有重要意义［1—3］。

众多国内外学者采用物理实验与数学模型的手段对波浪边界层开展研究。Hino等［4］和Jensen等［5］在U形管中测量了波浪边界层的流速剖面和床面剪切应力。孙亚斌等［6］采用格子Boltzmann方法对波浪层流边界层进行模拟，探讨了线性波和椭圆余弦波作用下的流速变化情况。陈杰等［7］采用一维垂线波浪边界层模型和M ellor-Yamada紊动模式模拟了线性波作用下的边界层流速剖面。吴永胜等［8］采用一阶边界层模型对波流共同作用下的边界层紊流结构进行分析，探讨了边界层内的波流非线性耦合机制。上述研究针对波浪边界层流速和床面剪切应力在一个周期内的变化规律取得了较好的进展，但大多基于流速在水平方向上均匀分布的一阶假定，对边界层内的时均流速分布未做深入分析。

实际波浪边界层的时均流动受到以下两个动力过程的共同影响。第一，波浪水质点运动具有水平流速梯度和垂向流速，而边界层内的黏性运动使得底床附近水平流速与垂向流速相位差不为90°，从而产生不为零的二阶波致雷诺应力，引起边界层内向岸方向的时均水流［9］；第二，波浪传播变形过程中会引起水体表层的向岸质量净输移和底层的离岸回流，引起边界层内不为零的时均水平压强梯度和离岸方向的时均水流［10］。Lin和H wung［11］的波浪水槽实验表明，浅化波浪边界层内的时均流速在底部为向岸，在上部为离岸，反映了两个动力过程的相互作用。近年来许多学者通过数学模型对这两者开展了针对性的研究，并探讨了它们的影响机制。H olmedal和M yrhaug［12］，Kranenburg等［13］采用二阶边界层模型对线性波和二阶斯托克斯波作用下的底部边界层时均水流进行模拟，分析了波致雷诺应力对边界层时均流速剖面的影响。Zhang等［14］在一阶边界层模型中考虑了离岸回流引起的时均水平压强梯度项，模拟分析了时均水平压强梯度对浅化波浪边界层时均流速分布的影响。这些研究重点探讨了波致雷诺应力或时均水平压强梯度其中一个动力过程的影响，尚未综合考虑两个过程的共同作用。

本文建立了二阶波浪边界层模型，同时考虑了波致雷诺应力和时均水平压强梯度的影响。受限于实验设备尺度，在波浪水槽内完成的紊流边界层实验尚不多，本文将初步采用已有的层流边界层实验数据来验证数学模型。在此基础上，探讨浅化波浪边界层内的流速分布特性及其影响机制。

2　数学模型

2.1二阶波浪边界层控制方程

二阶波浪边界层控制方程是基于雷诺平均的Navier-Stokes方程的简化。由于边界层厚度很薄，通常假定边界层内的水平压强梯度在层内均匀分布且等于上边界自由流动区的水平压强梯度。与一阶方程相比，二阶方程中考虑了水平对流项和垂向流速，能更好地描述波浪传播变形条件下的边界层流动特性。二阶波浪层流边界层的动量方程和连续方程可表示为：

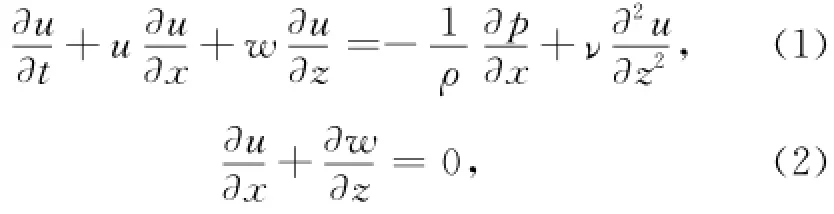
式中，u为水平速度，w为垂向速度，p为压强，ρ为水体密度，取1×103kg/m3，υ为水体运动黏滞系数，取1×10-6m2/s，t为时间，x为水平坐标（向岸为正），z为垂向坐标（向上为正）。式（1）左侧第二项和第三项分别为二阶水平对流项和垂向对流项，包含了波致雷诺应力的影响；式（1）右侧第一项为水平压强梯度项，包含了离岸回流的影响。这3项的确定是求解边界层模型的关键。

2.2二阶对流项的处理

针对某一特定位置，认为其局部两侧的波面形态沿程变化很小，水质点速度的空间梯度主要取决于自身的相位差，可采用下列关系式将水平流速梯度转化为流速对时间的导数：

式中，c为波浪速度。这种处理方法将方程简化为垂向一维，在保证计算精度的同时可有效提高计算效率［12—13，15］。式（3）在线性波理论和斯托克斯二阶波理论中是适用的。

结合连续方程，垂向流速可通过下式计算：

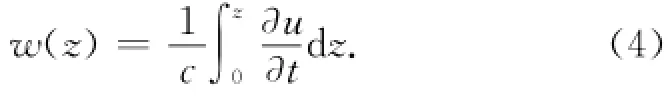
2.3水平压强梯度项的处理

水平压强梯度可分解为波浪压强梯度项和时均（水流）压强梯度项之和：

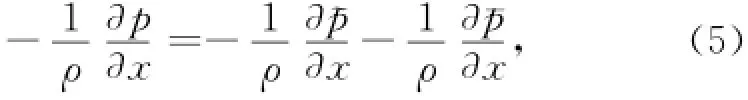
式中，波浪线和水平线上标分别表示某一物理量X的波浪和水流分量：

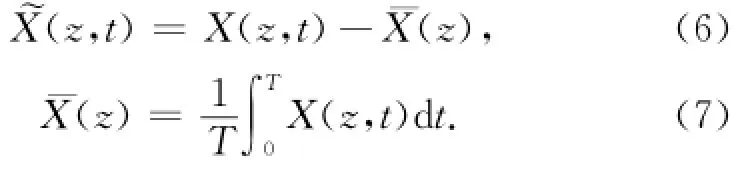
波浪压强梯度是由于波浪振荡运动引起的，可表示为：

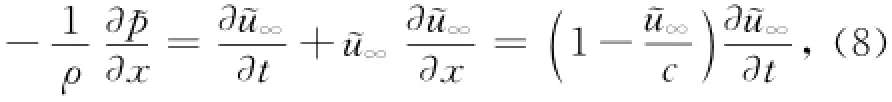
式中，u∞是上边界处的波浪自由振荡速度。

水平压强梯度项沿水深不变，反映了离岸回流的影响。Zhang等［14］发现该水平压强梯度对边界层时均流速分布具有重要影响。这一项在模型中通过自动迭代给定，以满足上边界处的计算时均流速接近于实测值。

2.4边界条件和数值格式

在床面上采用流速无滑移条件：

式中，z0为理论床面零点。

在上边界处采用零通量条件：

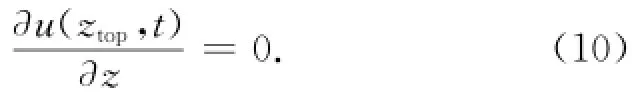
采用隐式有限差分格式离散控制方程。模型网格采用对数增大的变网格步长以保证近底流速梯度很大的区域有足够的计算精度。计算敏感性分析表明，当模型上边界ztop超出两倍边界层厚度处时，对边界层内流速计算的结果影响很小。在一个波周期内取100～500个计算步长，模型计算的初始时刻给u很小的正值。计算收敛条件为前后两个波周期内u的最大相对误差不超过1×10-5。试算结果表明模型可以很好地复演一阶和二阶斯托克斯波层流边界层解析解。

3　计算结果及分析

Lin和H wung［11］在国立成功大学台南水工试验所的波浪水槽中对斜坡上浅化波浪作用下的底部边界层进行了测量。水槽长为9.5 m、宽0.3 m、高0.7 m，底床为光滑定床。波高0.053 m、周期1.41 s的规则波正向入射于1∶15的斜坡上。在破波带外浅化区域布置10个测量断面，分别使用波高计和LD V测量水面高程和边界层内流速的时间序列。实验布置示意图如图1所示：

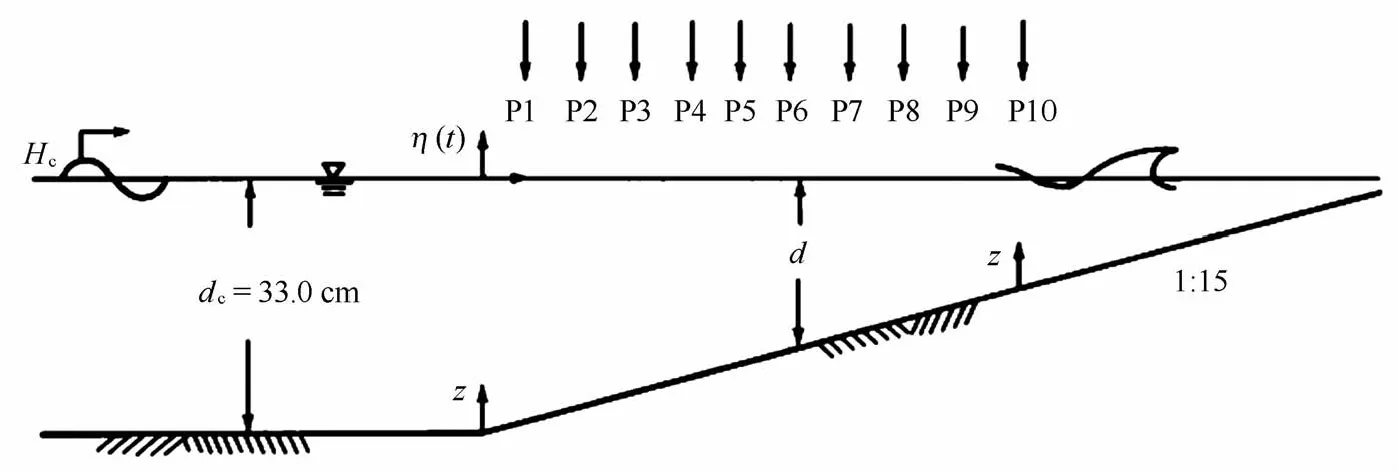
图1　Lin和H wung实验地形及测点布置示意图［11］Fig.1 Sketch of wave flume and location of measurements（extracted from Lin and H wung［11］）

选用P4、P8、P10三个断面的实测数据对模型进行验证，水深分别为0.157 m、0.11 m和0.085 m。计算区域上边界高度为ztop= 0.005 m，采用上边界处的实测波浪自由振荡速度作为模型输入条件。垂向布置200个网格，一个周期内计算500个时间步长。

波浪雷诺数Re是衡量边界层流态的重要指标。根据Lin和H wung［11］对实验数据的处理方法，波浪雷诺数取为为自由流速向岸方向幅值，T为波浪周期。结果表明3个断面处的波浪雷诺数介于1.57×104和4.11×104之间，多数时刻边界层处于层流状态，这与实验观察到的现象一致。

3.1流速剖面验证

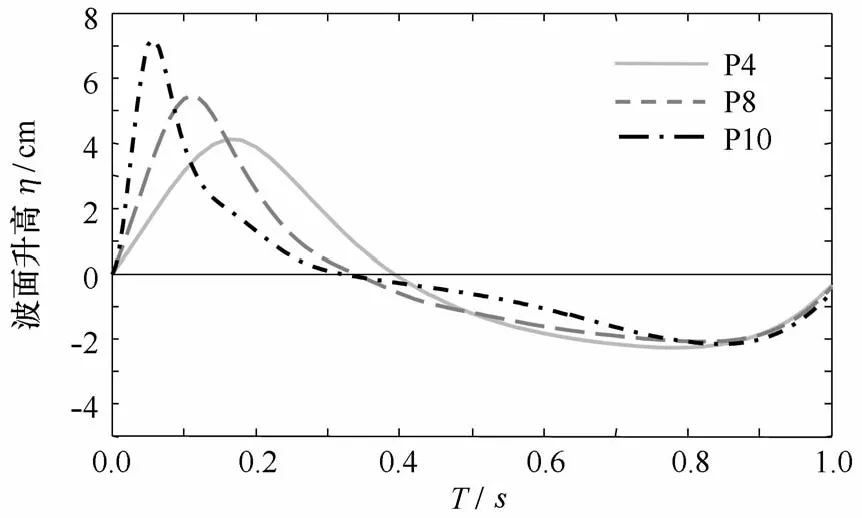
图2　P4、P8、P10处波面变化过程Fig.2 Temporal variations of the water surface elevation measured at P4，P8 and P10

图2给出了P4、P8、P10处一个周期的波面变化。图3给出了P4、P8、P10处的上边界自由流速时间序列和各个相位的瞬时流速剖面计算结果。图中实线为本文同时考虑时均水平压强梯度和波致雷诺应力影响的二阶边界层模型计算结果，点划线为参考Kranenburg等［13］不考虑时均水平压强梯度影响的二阶边界层模型计算结果，虚线为Zhang等［14］不考虑波致雷诺应力影响的一阶边界层模型计算结果。如图2所示，从P4到P10随着水深的减小，波浪浅化使得波峰变得陡峭而波谷变得平坦，峰谷不对称程度增强。图3中的上边界自由流速变化也呈现相同的趋势，加速阶段（相位A—C）历时缩短，减速阶段（相位C—G）历时增加。计算结果表明，不考虑波致雷诺应力的一阶边界层模型虽能较好模拟流速剖面上端离岸方向倾斜的趋势，但近底流速的计算误差较大。这一趋势从P4到P10逐渐明显，这是因为波浪浅化引起波高增大和离岸回流变强。不考虑时均水平压强梯度影响的二阶边界层模型没有考虑离岸回流影响，虽然计算得到流速剖面在床面附近与实测数据较为接近，但不能复演流速剖面上端离岸方向倾斜的趋势。本文模型改进了计算精度，主要体现在近底流速外突的位置和幅值以及流速剖面上部离岸倾斜趋势的捕捉，特别在向岸加速阶段（相位A—C）。

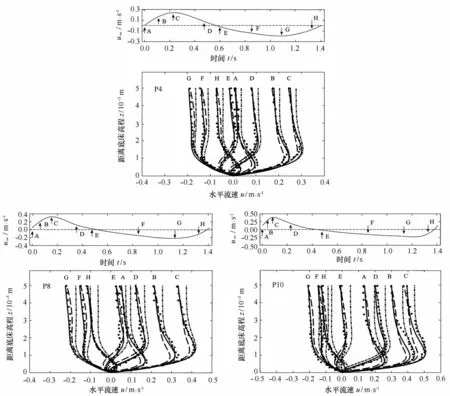
图3　P4、P8、P10处瞬时流速剖面计算值（实线：本文模型，点划线：不考虑时均水平压强梯度影响，虚线：不考虑波致雷诺应力影响，实测值：实心点）Fig.3 Comparison ofinstantaneous velocity profiles at P4，P8 and P10 between experimental data（dots）and simulated results neglecting the mean horizontal pressure gradient（dash dot lines），neglecting wave Reynolds stress（dash lines），and considering both（solid lines）

图4给出了实测与计算的波浪振荡速度幅值对比。模型较好地复演了波浪浅化过程中逐渐增大的波峰和波谷速度不对称性。从P4到P10波峰变得更加陡峭而波谷变得更加平坦，使得向岸方向振荡速度幅值大于离岸方向。二阶边界层模型的计算结果比起一阶模型略有改进，但总体上差别不大。

图5给出了时均流速剖面的对比。从图中可以看出，各点的实测时均流速都呈现出底部向岸上部离岸的变化特征。从P4到P10受到波浪浅化变形的影响，近底向岸流速和上部离岸流速都有缓慢增大的趋势，垂向流速梯度逐渐增大。不考虑波致雷诺应力影响的一阶边界层模型低估了近底流速和高估了上部流速。不考虑时均水平压强梯度影响的二阶边界层模型得到的流速剖面在整个区域内均为向岸方向，流速量值偏大且无法复演上部离岸的变化特征。同时考虑波致雷诺应力和时均水平压强梯度对准确模拟边界层流速分布特征有重要影响，特别是近底向岸最大时均流速的位置和量值和实验数据吻合很好。

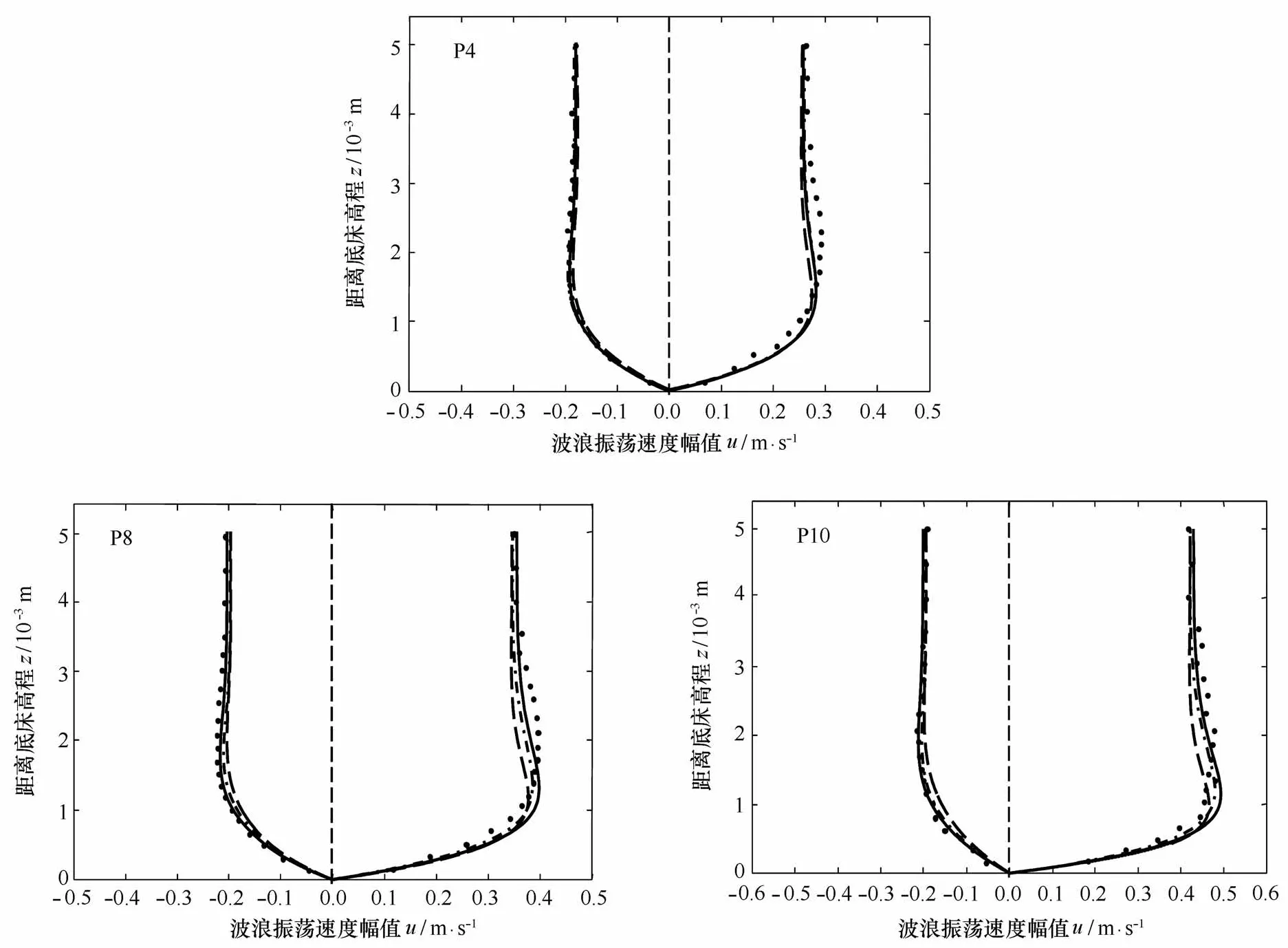
图4　P4、P8、P10处波浪振荡速度幅值计算值（实线：本文模型，点划线：不考虑时均水平压强梯度影响，虚线：不考虑波致雷诺应力影响，实测值：实心点）Fig.4 Comparison of wave velocity amplitude profiles at P4，P8，P10 between experimental data（dots）and simulated results neglecting the mean horizontal pressure gradient（dash dot lines），neglecting wave Reynolds stress（dash lines），and considering both（solid lines）

图6给出了P4、P8、P10的时均水平压强梯度迭代过程。从P4到P10时均水平压强梯度分别收敛于9.8×10-4Pa/m，1.8×10-3Pa/m，2.0×10-3Pa/m，迭代次数约为7步。由图可知波浪浅化变形引起波高增大和底部回流增强，相应的时均水平压强梯度也逐渐增大。

模型验证时在3个点处均采用同一个计算区域上边界ztop= 0.005 m。针对波浪边界层数值模拟而言，当模型上边界高于边界层厚度时（即上边界位于自由流速区），对计算结果的影响很小。图4所示，3个点处的波浪振荡速度幅值在z＞0.004 m时变化很小，可认为边界层厚度均在0.004 m附近。因此，本文统一选取ztop= 0.005 m对计算结果影响不大。图7给出了不同上边界高度设置下（ztop分别为0.005 m、0.006 m、0.008 m、0.01 m）计算得到的P10点时均流速剖面，计算结果没有发生显著变化。

3.2影响机制分析

为了进一步探究不同动力过程对边界层时均流速剖面的影响机制，对式（1）进行周期平均和沿水深积分可得到：

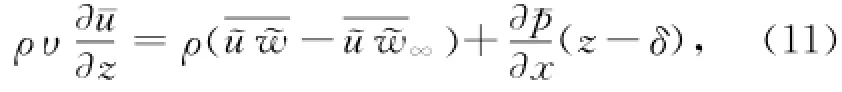
式中，等式左边反映了边界层内任意高度的时均剪切应力，这一项控制着时均流速的垂向分布，等式右边第一项表示由波致雷诺应力引起的由边界层外向边界层内的时均动量传递，等式右边第二项表示时均水平压强梯度的贡献，其中δ表示上边界高程。

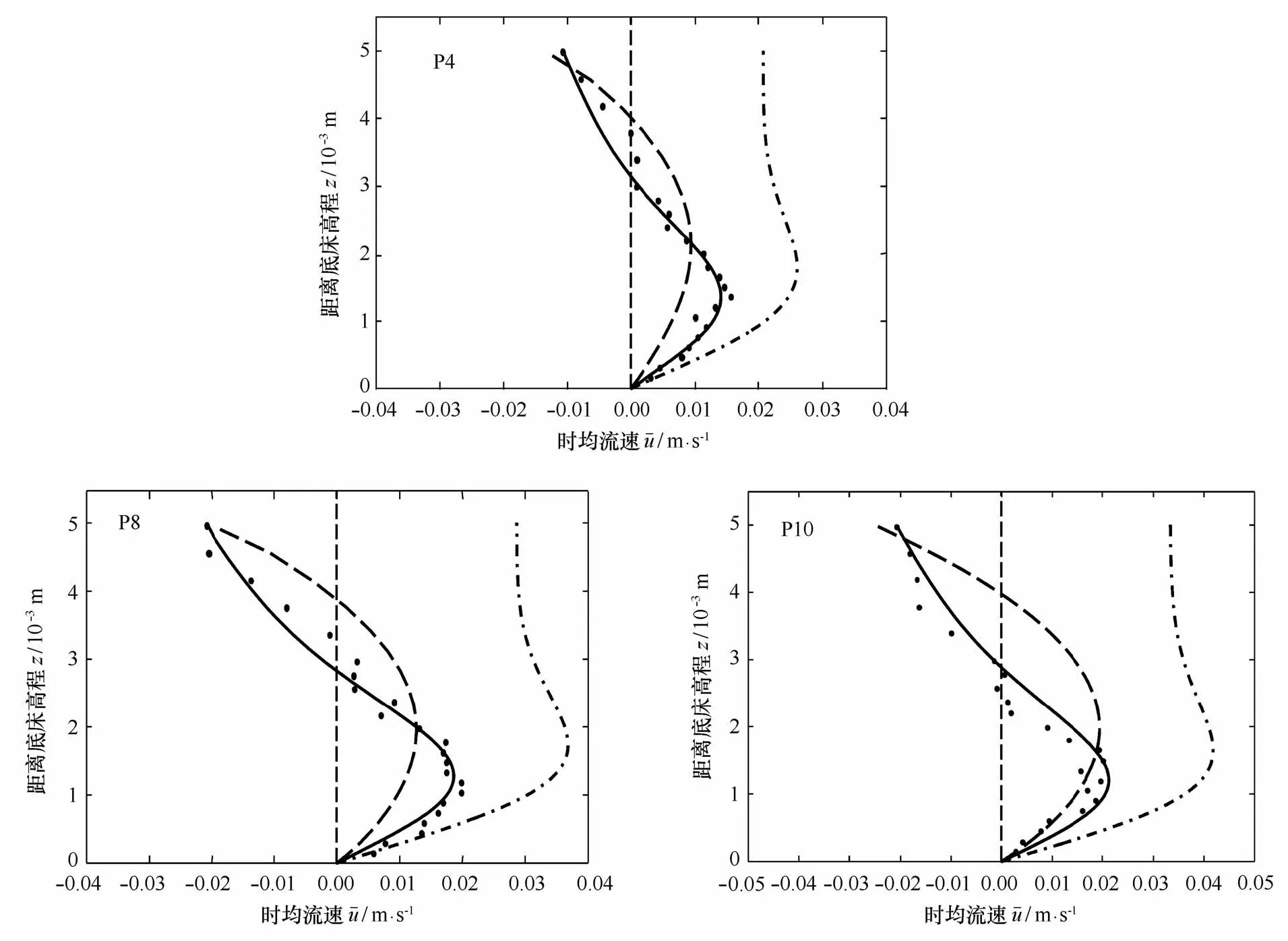
图5　P4、P8、P10处时均流速计算值（实线：本文模型，点划线：不考虑时均水平压强梯度影响，虚线：不考虑波致雷诺应力影响，实测值：实心点）Fig.5 Comparison of mean velocity profiles at P4，P8，P10 between experimental data（dots）and simulated results neglecting the mean horizontal pressure gradient（dash dot lines），neglecting wave Reynolds stress（dash lines），and considering both（solid lines）

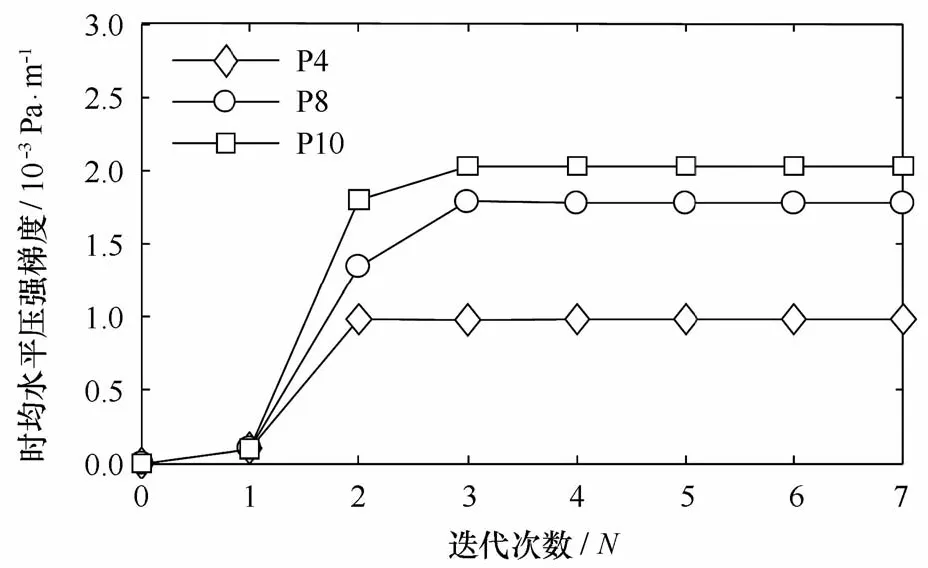
图6　时均水平压强梯度的迭代过程Fig.6 Iterative process of the mean horizontal pressure gradient

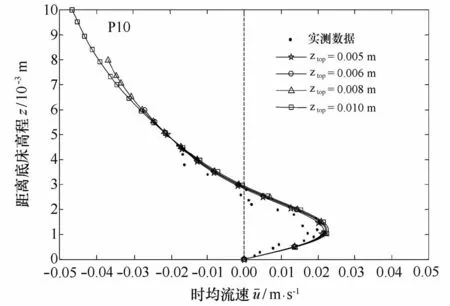
图7　不同模型上边界高度设置下的P10点时均流速剖面计算结果对比Fig.7 Comparison of the calculated mean velocity profiles at P10 with different upper boundary elevations

图8给出了3个断面处各影响项的垂向分布情况。从图8a中可以看出，时均剪切应力在底部为正值，在上部区域变为负值，接近上边界附近趋近于零。图8b中的波致雷诺应力影响项的分布特征与图8a比较接近，底部为正值，但随着高度的增加则趋近于零。图8c中时均水平压强梯度影响项沿垂向均为负值，且随着波浪浅化变形，因波高增加和离岸回流增强而逐渐增大。总体而言，靠近床面处，时均剪切应力主要受波致雷诺应力的影响，表现为正值，趋向于引起向岸流动；在边界层上部区域，波致雷诺应力影响逐渐减小，时均水平压强梯度占主导作用，时均剪切应力表现为负值，趋于引起离岸流动。

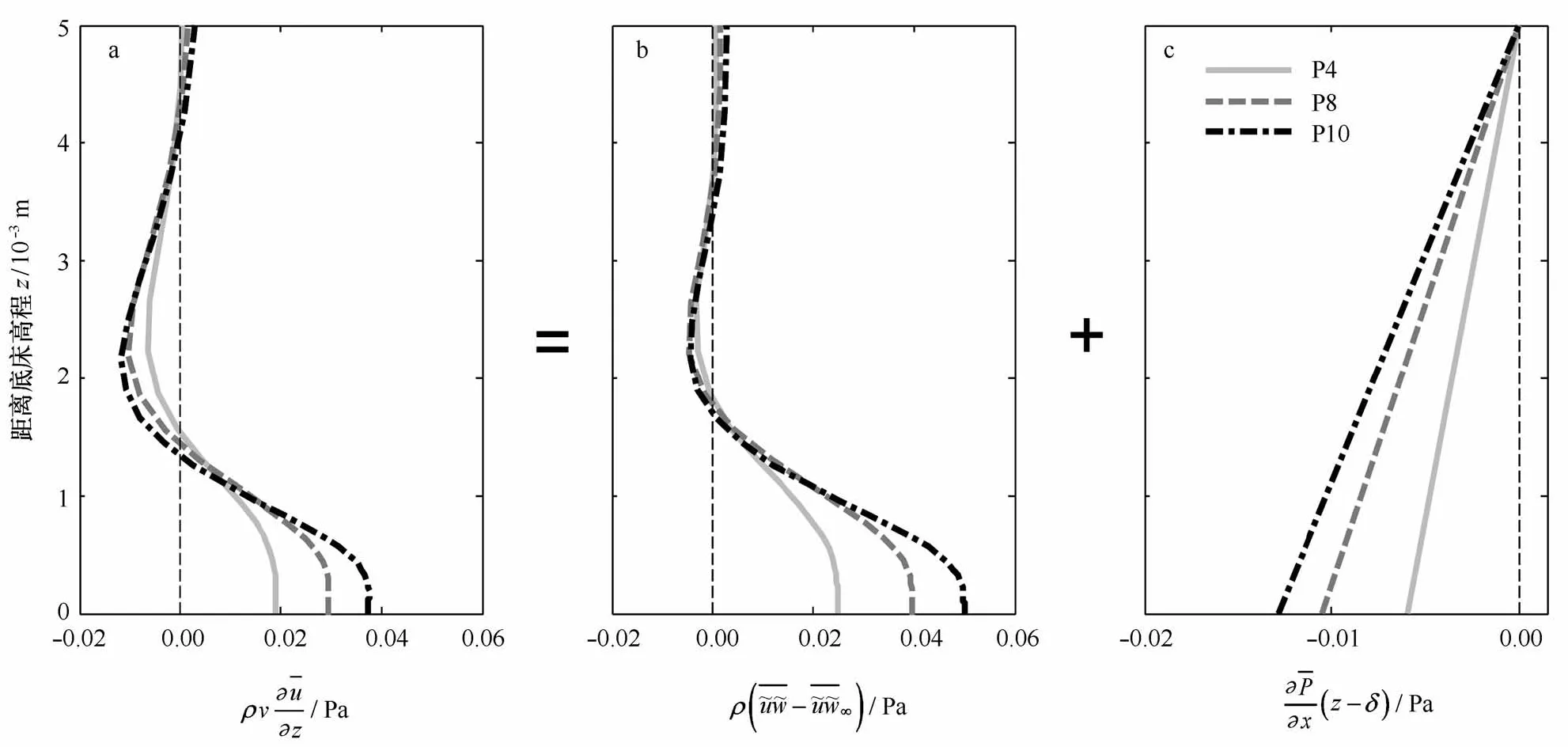
图8　边界层时均流速影响机制Fig.8 Effects of various terms on the mean velocity distribution

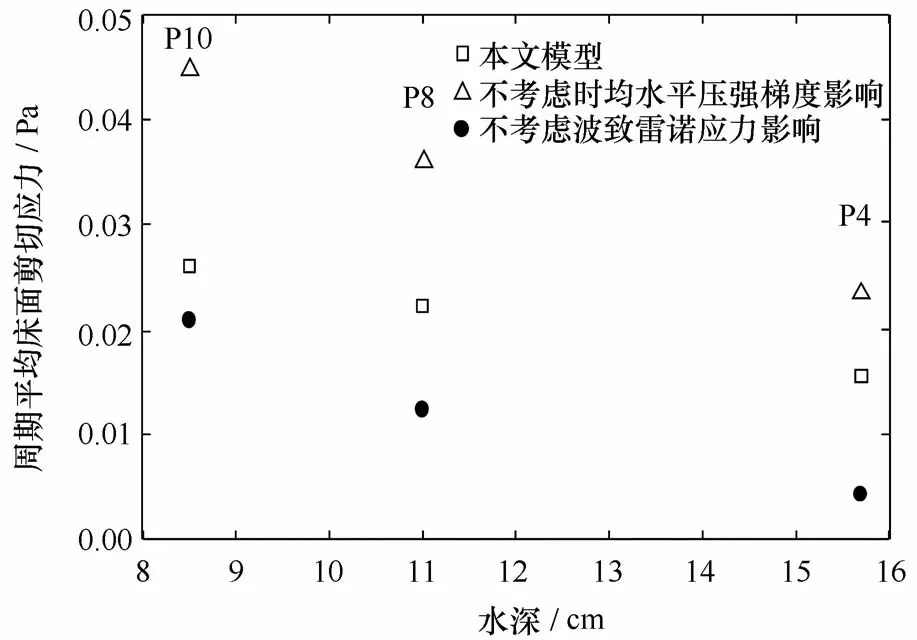
图9　周期平均床面剪切应力计算结果的对比Fig.9 Comparison of calculated period-averaged bed shear stress

图9给出了周期平均床面剪切应力的计算结果比较。从P4到P10，随着水深变浅和波浪浅化变形，近底时均流速增大，周期平均床面剪切应力均为正值且逐渐增大。波致雷诺应力会增强近底时均向岸水流，趋向于增大床面剪切应力，而时均水平压强梯度反映了底部回流的影响，趋向于减小床面剪切应力。

4　结论

本文建立了二阶波浪边界层数学模型，在模型中通过二阶对流项和时均水平压强梯度项考虑了波致雷诺应力和离岸回流的影响。采用浅化波浪层流边界层的水槽实验数据对模型进行验证，瞬时流速剖面、振荡速度幅值和时均流速剖面的计算结果均与实测数据吻合良好，同时考虑波致雷诺应力和时均水平压强梯度对准确模拟边界层流速分布特征有重要影响。流速分布特性及其影响机制分析表明，随着波浪的浅化变形，边界层内瞬时流速剖面离岸倾斜的趋势更加明显，波浪振荡速度幅值的不对称性逐渐增大，时均流速剖面“底部向岸、上部离岸”的变化特征越来越明显，垂向流速梯度逐渐增大。时均流速分布主要受波致雷诺应力和时均水平压强梯度的影响，在床面附近由波致雷诺应力占主导作用并趋于引起向岸流动，在上部区域由时均水平压强梯度占主导作用并趋于引起离岸流动。本文研究结果为将来进一步深入研究波浪传播变形条件下的紊流边界层动力过程提供了基础。

参考文献：

［1］Nielsen P.Coastal bottom boundary layers and sediment transport［M］.Singapore：W orld Scientific，1992.

［2］陈杰，刘静，蒋昌波，等.波浪作用下泥沙运动研究综述［J］.泥沙研究，2014（4）：74-80.Chen Jie，Liu Jing，Jiang Changbo，et al.Review of sediment transport under waves［J］.Journal of Sediment Research，2014（4）：74-80.

［3］汪亚平，高抒，贾建军.海底边界层水流结构及底移质搬运研究进展［J］.海洋地质与第四纪地质，2000，20（3）：101-106.W ang Yaping，Gao Shu，Jia Jianjun.Flow structurein the marine boundary layer［J］.M arine Geology & Quaternary Geology，2000，20（3）：101-106.

［4］Hino M，Kashiwayanagi M，Nakayama A，et al.Experiments on the turbulence statistics and the structure of a reciprocating oscillatory flow［J］.Journal of Fluid M echanics，1983，131：363-400.

［5］Jensen B L，Su mer B M，FredsØe J.Turbulent oscillatory boundary layers at high Reynolds nu mbers［J］.Journal of Fluid M echanics，1989，206：265-297.

［6］孙亚斌，张庆河，张金凤.振荡层流边界层运动的格子Boltzmann模拟［J］.水动力学研究与进展：A辑，2006，21（3）：347-353.Sun Yabin，Zhang Qinghe，Zhang Jinfeng.Simulation of oscillatory laminar boundary layer flow based on Lattice Boltzmann M ethod［J］.Chinese Journal of H ydrodynamics，2006，21（3）：347-353.

［7］陈杰，蒋昌波，刘虎英，等.M ellor-Yamada模型在波浪边界层中的运用［J］.海洋通报，2010，29（3）：253-256.Chen Jie，Jiang Changbo，Liu H uying，et al.Study of wave boundary layer based on M ellor-Yamada model［J］.M arine Science Bulletin，2010，29 （3）：253-256.

［8］吴永胜，练继建，张庆河，等.波浪-水流共同作用下的紊动边界层数值分析［J］.水利学报，1999（9）：68-74.W u Yongsheng，Lian Jijian，Zhang Qinghe，et al.Nu merical analysis of turbulent boundary layer under combined action of wave and current［J］.Shuili Xuebao，1999（9）：68-74.

［9］Longuet-Higgins M S.The mechanics ofthe boundary layer near the bottom in a progressive wave［C］//Proceedings of 6th Conference on Coastal Engineering，1958：184-193.

［10］Putrevu U，Svendsen I A.Vertical structure ofthe undertow outside the surf zone［J］.Journal of Geophysical Research，1993，98（C12）：22707-22716.

［11］Lin C，H wung H H.Observation and measurement ofthe bottom boundary layerflow in the prebreaking zone of shoaling waves［J］.Ocean Engineering，2002，29（12）：1479-1502.

［12］H olmedal L E，M yrhaug D.W ave-induced steady streaming，masstransport and net sedimenttransportin rough turbulent ocean bottom boundary layers［J］.Continental Shelf Research，2009，29（7）：911-926.

［13］Kranenburg W M，Ribberink J S，Uittenbogaard R E，et al.Net currentsin the wave bottom boundary layer：on waveshape streaming and progressive wave streaming［J］.Journal of Geophysical Research，2012，117：F03005.

［14］Zhang C，Zheng J H，W ang Y G，et al.M odeling wave-current bottom boundary layers beneath shoaling and breaking waves［J］.Geo-M arine Letters，2011，31（3）：189-201.

［15］Henderson S M，Allen J S，Newberger P A.Nearshore sandbar migration predicted by an eddy-diffusive boundary layer model［J］.Journal of Geophysical Research，2004，109（C6）：C06024.1-C06024.15.

李诚，张弛，隋倜倜.浅化波浪层流边界层流速分布特性的数值分析［J］.海洋学报，2016，38（5）：141-149，doi：10.3969/j.issn.0253-4193.2016.05.013

Li Cheng，Zhang Chi，Sui Titi.Numericalinvestigation on velocity distribution in the shoaling laminar wave bottom boundary layer［J］.Haiyang Xuebao，2016，38（5）：141-149，doi：10.3969/j.issn.0253-4193.2016.05.013

Numericalinvestigation on velocity distribution in the shoaling laminar wave bottom boundary layer

Li Cheng1，2，Zhang Chi1，2，Sui Titi1，2
（1.Key Laboratory of Coastal Disaster and Defence，Ministryof Education，Hohai University，Nanjing 210098，China；2.Collegeof Harbour，Coastaland Offshore Engineering，Hohai University，Nanjing 210098，China）

Abstract：An improved second-order nu merical modelfor wave bottom boundary layeris developed，which includes both effects of wave Reynolds stress and mean horizontal pressure gradient.The simulated instantaneous velocity profiles，oscillatory velocity amplitudes and mean velocity profiles in the laminar boundary layer beneath shoaling waves are in good agreements with the experimental data.Effects of various dynamic processes on the mean velocity distribution are discussed.Results revealthatthe mean velocity is directed onshore and offshorein thelower and upper regions of the bottom boundary layer，respectively，and this pattern becomes increasing obvious as wave shoals over a sloping bed.The near-bed onshore mean velocity is dominated by wave Reynolds stress related to the second-order advective terms，while the offshore mean velocity in the upper region is mostly due to the mean horizontal pressure gradient related to the undertow current.

Key words：wave shoaling；bottom boundary layer；mean velocity；nu merical simulation

*通信作者：张弛（1985—），男，福建省莆田市人，副教授，从事海岸泥沙运动与地貌形态动力学研究。E-mail：zhangchi＠hhu.edu.cn

作者简介：李诚（1989—），男，四川省乐山市人，从事海岸动力学研究。E-mail：lichenghsbc＠163.com

基金项目：国家自然科学基金项目（51209082）；交通运输部应用基础研究计划项目（2014329224330）；江苏省普通高校研究生科研创新计划（＃C XL X11_0450）。

收稿日期：2015-05-10；

修订日期：2015-07-21。

中图分类号：T V139.2

文献标志码：A

文章编号：0253-4193（2016）05-0141-09