数学课堂问题设计的五个度

张波

[摘要]教学过程中，课堂环境会随时发生变化，让课堂提问呈现出灵活性和独特性的特点，教师教学时必须正确认识到课堂提问的作用和价值，精心设计、合理运用课堂提问，将课堂提问的灵活性发挥出来，激发学生的创造性，培养学生的数学思维.

[关键词]数学课堂 问题设计

[中图分类号] G633.6 [文献标识码] A [文章编号] 1674-6058（2016）02-0006

问题是数学的心脏，好的课堂提问能有效地促进学生学习，激发学生的思维，在教学过程中，教师若能精心地设计数学问题，把握好问题设计的五个“度”，对于减轻学生负担，提高教学效率有着非常重要的意义。

一、问题设计的角度

数学问题的设计要选准角度，确定最佳的切入点.

首先，问题的角度要新颖，能引起学生的兴趣和注意.问题是新课开始的设问，教师应该确保问题能够引起学生的注意，努力将学生引导到白己创设的情境中去，活跃学生的思维.比如在进行“角边角”公理学习时，教师可以提出这样的问题：一块三角形的玻璃，若将其一个角打破，将其分成两块，是不是要把两块拼在一起，才能够得到原本的形状？这样的问题很容易激发学生的学习兴趣，能让学生在思考的过程中进入到“角边角”的三角形全等判定公理学习情境中。

其次，设置的问题，应该有一定的启发性，能够激发学生的思维，让其更加积极地思考，从而达到教学目的.例如，观摩教师在教学二次函数这节课时，授课教师先安排学生解方程x?-4x+3=O，然后问学生：如何求抛物线y=X?-4x+3与x轴交，x轴的坐标？很多学生都默不作声.教师提出这个问题的目的是想让学生将抛物线y=x?-4x+3与x轴的交点的横坐标和方程x?-4x+3=0的根联系在一起，让学生从这个问题联想到直线和曲线的交点横坐标，但是学生可能不记得x轴方程，所以解题时不知道怎样解.这也直接说明了教师设计的问题切入点和其期待的效果存在一定的差别.而另一个教师在处理这个问题时，选择的是其他方法，其依次提出了下面几个问题.

师：方程x?-4x+3=O相当于函数y=x?-4x+3=0的函数值等于多少？

生：0.

师：当函数值为O时，其图像上点的坐标中，哪个坐标为0？

生：纵坐标.

师：纵坐标为0的点具有什么位置特征？

生：都在x轴上.

师：那么怎样去求抛物线y=x?-4x+3与x轴的交点的横坐标呢？

生：抛物线y=X?-4x+3与x轴的交点在x轴上，x轴上的点的纵坐标为0.纵坐标力o就是函数值为0.即X?-4x+3=0.这个方程的根就是抛物线y=X?-4x+3与x轴的交点的横坐标，也就是x1=1，x2=3.

在师生解答问题时，第一个问题能够帮助学生全面地理解二次函数和一元二次函数的关系，教师提出这个问题的日的是为了帮助学生了解二次函数和一元二次方程关系.而第二个问题的提出，能够帮助学生理解函数值和图像上点的纵坐标关系.第三个问题的提出可以让学生更好地理解x轴上面点坐标特征，教师提出这个问题的日的是让学生理解并掌握x轴上点纵坐标的特征，也就是纵坐标是0.第四个问题的提出是为了帮助学生综合考虑二次函数和一元二次方程，把问题转变成为一元二次方程的求根问题，教师提出这个问题的日的是帮助学生更好地理解掌握上面两个关系，把抛物线和x轴的交点横坐标求解问题转化成进行相应一元二次方程根的求解问题.问题的提出和教学的日标本身是一致的，这能够让学生更加积极地思考，从而提高提问的有效性，切实做好数学教学.

二、问题设计的难度

思维源于问题.在设计问题时应该有一定的难度，这样才能够将学生的求知欲望和好奇心激发出来，让学生能够通过自己的努力取得学习成果.

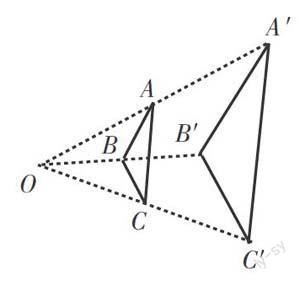
例如，在位似一节课中，教师为了引导学生发现位似图形的性质，提出这样的问题：用刻度尺量一下AO、A'O的长度，求出其比值，与两个三角形的相似比比较；再量BO、B'O的长度，求出其比值与两个三角形的相似比比较.

这个问题设计的不足之处在于问题的梯度太小，操作性太强，思维含量较少.教师提出这个问题后，学生只需依照问题的要求按部就班地进行即可解决.在这个过程中，教师是“设计师”，学生是“执行者”.教师可以采用类比研究的方法提出问题，以提高问题思维的含量.如：在相似图形中，对应线段成比例，那么在位似图形中，这个结论还成立吗？请大家设计方案来检验这个结论是否成立.怎样解决这个问题，可以引导学生采用推理的方法进行严谨的逻辑分析，也可以采用度量的方法进行归纳猜想.这样设计，既体现了知识之间的联系，又符合学生的“最近发展区”.