§1.1回归分析的基本思想及其初步应用（第3课时）教学案例

姜有军

中图分类号：G633.6 文献标识码： A 文章编号：1992-7711（2016）10-036-01

教学目标：

1. 使学生会根据观测数据的特点来选择不同的回归模型。

2. 使学生通过探究体会到有些非线性模型通过变换可以转化为线性回归模型。

教学重点：通过探究使学生体会有些非线性模型通过变换可以转化为线性回归模型，了解在解决实际问题的过程中寻找更好的模型的方法。

教学难点：了解函数的图象特点，选择不同的模型建模。

教学过程：

一、复习提问（多媒体课件展示，学生回顾所学内容5分钟之内回答）

1.回归分析，其步骤；2. 线性回归模型；3. 衡量回归方程的预报精度的方法；（1）残差平方和法 （2）残差图法（3）利用相关指数R2刻画回归效果。

4. 建立回归模型的基本步骤 。

设计目的：通过反复，主要让学生熟练掌握回归分析的基本思想和步骤，以及掌握衡量回归方程的预报精度的方法。

二、引入新课

一只红铃虫的产卵数和温度有关，现收集了7组观测数据列于下表中，试建立与之间的回归方程。

教师：先来分析这道题的解题思路？

学生：先作散点图。后根据图求对应的方程。

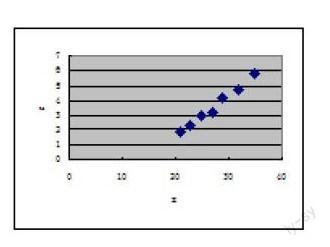
（教师让学生描述求回归方程的步骤，第一步：作散点图，第二步：确定回归方程的类型，第三步：求方程。教师演示用电脑做好的散点图）

教师：观察右图中的散点图，它们是线性相关吗？

学生：发现样本点并没有分布在某个带状区域内，即两个变量不呈线性相关关系，所以不能直接用线性回归方程来建立两个变量之间的关系.

三、讲授新课：（探究非线性回归方程的确定）

教师： 如果散点图中的点分布在一个直线状带形区域，可以选线性回归模型来建模；如果散点图中的点分布在一个曲线状带形区域，就需选择非线性回归模型来建模，本节课就来探讨如何建立它的模型？

（学生合作交流， 根据散点图找近似的函数模型）

学生：根据已有的函数知识，可以发现样本点分布在某一条指数函数曲线的周围（其中是待定的参数），故可用指数函数模型来拟合这两个变量。

学生：也可以看成二次型函数y=c3x2+c4来做。

教师：很好，看来同学们预习的不错！接下来先研究y=c1e ，如何待定方程中c1与c2？

学生： 在上式两边取对数，得lny=c2x+lnc1，再令z=lny，则z=c2x+lnc1，而z与x间的关系如下：

观察与的散点图，可以发现变换后样本点分布在一条直线的附近，因此可以用线性回归方程来拟合。

教师：既然找到了方法同学们自己完成。

（学生利用计算器在10分钟内算得a=-3.843，b=0.272，z与x间的线性回归方程为z=0.272x-3.843，因此红铃虫的产卵数对温度的非线性回归方程为y=e0.272x-3.843.）

教师：根据散点图就一定能得到这是以e为底的指数型函数吗？其它底数的指数型函数可以吗？如果设行吗？（通过不断提问，发散学生的思维）（大多数学生半信半疑，等待教师引导，有个别学生茅塞顿开）

学生甲：可以，同样可以待定c，a.

教师：如何待定c，a？

学生甲：将两边取以a为底的对数？

教师：非常棒！但以a为底的对数方便查表吗？

学生乙：噢，但可以取常用对数呀。

（此时课堂气氛已到了一个小高潮，同学们都在积极思考，感觉才像用数学解决问题。）

教师：很好！那我们来一起完成它。

因为，y=cax，所以，lgy=lg（cax），即，lgy=lgc+xlga，令z=lgy ， lgc=b，lga=d，则z=dx+b，它是线性的，再利用最小二乘法求出d，b，再进一步算出y关于x的方程。看来这样也是可以算出其对应的方程。

教师：我们再来研究同学们前面提到的二次型函数 y=c3x2+c4.如何求解c3与c4 ？ （学生思考后陷入僵局）

教师：其关键在于如何通过适当的变换，将非线性回归问题转化成线性回归问题。

学生丙：直接换元，将x2换成t，则就可将非线性换成线性加以解决。（此时他很激动，其他同学对他刮目相看）

教师：很牛！这位同学说的你们下来解。我现在有这样一个问题：好像散点图不一定是不含一次项的二次函数呀？若设y=ax2+bx+c可以吗？

学生丁：这不跟前面一样吗，直接换x2.

教师： 直接换x2为谁？是x吗？

学生：不对。（异口同声）

教师：那怎样解a，b，c？

（此时教室有一片哗然，同学们又开始讨论了，有一个小组的同学举手示意）

学生：老师，y=ax2+bx+c与y=c3x2+c4不同之处就是多了一次项，我可以将它先配方转化成后面的形式加以解决。

教师：好，这位同学上黑板来解。

四、课堂小结

教师：本节课通过这道例题，我们发现了非线性问题也可以转化成线性问题来解决，下面谁将所学技巧加以总结。

学生：指数型的函数要通过对数变换后在换元，二次函数要通过配方化成不含一次项的后换元。