彩色半透明纸在初中数学课堂中绽放独特魅力

王涛

彩色半透明纸是非常有力的数学实验的工具，利用它的透明性、可移动、多种颜色、易观察等特性可以使抽象问题直观化，静态问题动态化. 在平时教学中，我也摸索着用彩色半透明纸来辅助教学，或多或少地发现了它所展现的独特魅力，下面我将结合几个案例，将彩色半透明纸辅助教学的独特魅力与大家分享.

一、彩色半透明纸既透明又拥有色彩更易引起关注

在苏科版七年级上册4.3用一元一次方程解决问题第一课时，我们进行过月历游戏来探索月历中数字的排列规律. 先让学生在准备的月历上用笔任意框住某一行的相邻3个数、某一列的相邻3个数、一个数以及它的上下左右相邻的4个数等等来分别研究它们的排列规律. 接着又让学生独立设计框图，并探索它们的排列规律（如：平行四边形框图、H型框图、I型框图、X型框图等等）. 多次用笔在月历画框图，会在月历上留下多处痕迹，一旦所画的框图有所重叠，势必会影响观察效果. 如果事先已经用彩色半透明纸制作好的各种框图，那么活动时就不用担心前后框图会有所重合，月歷也可以重复使用，而且每个框图所对应的数的排列规律可以直接记录在框图上. 用彩色半透明纸制作框图不仅仅因为它是半透明的，不遮挡月历上的数字，还有一个重要的原因就是它是彩色的，覆盖在月历上很容易被关注.

二、利用彩色半透明纸好复制、易辨别的特点来化静为动

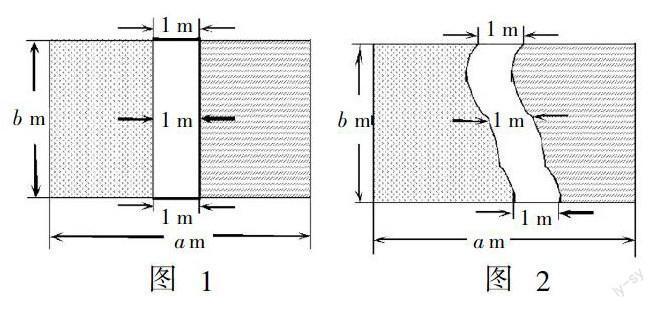
在苏科版七年级上册12.2证明第一课时有这道例题，如图1长方形草坪中间的一条1 m宽的直道改造成如图2的1 m宽的“曲径”.两条小道占用草坪的面积相等吗？如何证实你的结论？

通常我们在分析这道例题时，会在黑板上画左、右两边的草坪拼合好的图，让学生被动地接受两条小道占用草坪的面积相等. 学生并没有经历草坪的移动与拼合的过程，也就无法真正理解真谛，此时如果用彩色半透明纸来辅助教学就能达到事半功倍的效果. 课前教师将图（1）与图（2） 印制在学案上（但草坪区域的阴影已清除），课堂上要求学生分组用彩色半透明纸覆盖在图（1）与图（2） 描出小道左右两边草坪的边框并剪下（两边草坪选用不同颜色），然后组内合作操作，确保左右两边草坪中一边草坪不动，移动另一边草坪，使两边的草坪无缝隙拼合. 在整个操作过程中，由于彩色半透明纸的色彩与透明性，学生可以清楚地看到小道慢慢被半透明纸所覆盖，也可以轻松地辨别两边的草坪在何处拼合. 在小道慢慢被覆盖的同时，图（1）与图（2）中原覆盖的部分慢慢出现了空白区域，这就引发了学生思考并得出结论. 最后让学生在长方形草坪中自己设计一条1 m宽的小道，经历设计、描边、剪纸、移动等一系列的活动后，学生对这道题的理解又上升到另一个高度，再也不是被动记忆了. 用彩色半透明纸来化静为动，可以使学生的思考过程变得具体化、形象化，从而难点也易突破.

三、彩色半透明纸让重叠部分更易观察

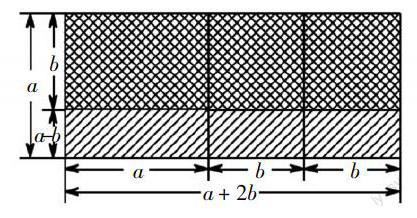
比如苏科版义务教育教科书《数学实验手册》七年级下册“拼图”中有一个活动是分别选取适当数量的A型（边长为a的正方形）、B型（边长为b的正方形）、C型（长为a、宽为b的长方形）三种纸片，如果允许覆盖（视为减去），你能尝试拼出边长分别为a + 2b，a - b的长方形吗？

本实验借助于纸片进行拼图活动，经历操作、探究、解决问题的过程，探索拼图与整式乘法以及因式分解之间的内在联系. 用不透明的纸片进行拼图，不少学生很难感受覆盖，即使用白色透明纸也很难观察与真正理解实质. 这时就要选用两种颜色的彩色半透明纸片来实验，因为两种颜色的彩色半透明纸在重叠时会产生第三种颜色，所以在实验过程中根本不用担心“被减去”的部分会被纸片遮挡而不易观察（如下图）.

四、彩色半透明纸让抽象问题直观化

彩色半透明纸还适用数与形关系的研究，比如二次函数的图像和性质，教材先研究了最简单的二次函数y = ax2（a ≠ 0），然后研究了y = ax2 + k（a ≠ 0），y = a（x - h）2（a ≠ 0），y = a（x - h）2 + k（a ≠ 0）这三个二次函数的图像及性质，而这三个稍复杂的二次函数的图像均是由y = ax2（a ≠ 0）的图像平移得来的. 传统教学常常要求学生前一天晚上先画几个规定二次函数的图像，课堂上就利用这几个图像来研究平移. 但是实际教学中发现，效果差强人意. 图像的平移规律对学生来说始终是一个难点.

如何突破这个难点呢？利用好彩色半透明纸，对于这个问题的解决起了重要的作用. 我们可以要求学生前一天晚上在纸上画一个平面直角坐标系，并在若干张彩色半透明纸描出y = 2x2的图像（不含平面直角坐标系）. 课堂上，让学生将事先画好的抛物线摆放在y = 2x2，y = 2x2 + 2，y = 2x2 - 2的对应的位置上. 直观的发现三者之间的关系，进行猜想，然后移动放在y = 2x2位置上的抛物线，使它依次与y = 2x2 + 2，y = 2x2 - 2对应的位置上的抛物线重合. 这样学生可以更加直观地感受到这三者图像之间存在着上下平移的联系，再要求学生分组将事先画好的抛物线放置y = 2x2 + k（k可以任意变化）的对应的位置上，来研究它们与抛物线y = 2x2的图像的联系并验证. 为什么这些图像之间存在上下平移的联系？目的是引导学生从借用彩色半透明纸的直观猜想到归纳，最后用数学知识去验证猜想和归纳的准确性. 即对于一般的点A（m，2m2）和B（m，2m2 + k），横坐标不变，纵坐标 + k，依照点的平移规律，相当于点A向上或向下平移了|k|个单位变成了点B，所以整个图像呈现上下平移的状态！这样就从数和形两方面验证了平移规律“上加下减”，利用平移更好地研究y = ax2 + k（a ≠ 0）的性质. 有了彩色半透明纸，抽象的二次函数的平移，每名学生都可以实验起来.

利用彩色半透明纸进行辅助教学，直观具有鲜明，生动和真实等特点. 容易引起学生的学习兴趣，增强感知的积极性. 它用几何直观的方式来说明数学的内在道理，深入浅出，可以引导学生达成对学的深度理解，帮助学生有效地转变学习方式，使学生逐步学会数学思维的物质实践方法，掌握数学研究的规律，培养理性思考问题的习惯.