运用一次二阶矩法计算焊接结构可靠性

杨晨 钟武烨

摘 要：与电子产品相比，焊接结构有许多不同点：失效模式复杂；以耗损型故障为主；大多是专用件，标准件少；数据缺乏。因而，机械产品可靠性无法像电子产品那样，通过查询标准数据手册获得。该文基于应力-强度干涉模型，使用一次二阶矩法对焊接结构的可靠性进行计算。

关键词：焊接结构 可靠度 一次二阶矩法

中图分类号：TU312 文献标识码：A 文章编号：1674-098X（2016）01（b）-0048-02

Abstract：Compared with the electronic products，there are many different characteristics of the reliability of welding structures：the failure mode is complex；mainly wear fault；mostly special parts and few standard parts；lack of data.As a result，the reliability of welding structures cannot be obtained by referring to standard data manual.In this paper，based on the stress-strength interference model，we use first order second moment method to calculate the reliability of the welding structures.

Key Words：Welding structures；Reliability；First order second moment method method（FOSM）

在可靠性分析中，基本零件可靠度的计算是重要的一环。对于电子产品来讲，可以查询相关的标准手册，而机械产品由于标准件少，数据缺乏，无法简单查得，必须进行计算。

利用概率设计法定量分析机械产品可靠性的主要步骤如下。

（1）失效模式的确定。

（2）根据失效的原因确定失效的判据。

（3）确定影响强度和应力的因素及相应的计算公式，建立功能函数。

（4）利用一次二阶矩法计算可靠度。

在计算时可以将零件实际受到的应力与材料强度代入求解，这是合乎人们的一般印象的。但在工程实践中，经常发生应力远小于材料强度的断裂事故，这使人们反思，是否还有隐藏的导致材料断裂的机理。

1920年，Griffith提出了裂口理论，认为材料中存在微小裂纹，这些裂纹在应力大于某一临界值时，会发生极速扩展，造成零件断裂失效。

焊接结构由于工艺上的原因，普遍存在热裂纹、再热裂纹、冷裂纹、层状裂纹、应力腐蚀裂纹等微小裂纹，在进行可靠性分析时必须重点分析其发生裂纹扩展的概率。

1 应力-强度干涉模型

从可靠性角度考虑，影响机械产品失效因素可概括为应力和强度两类。当应力小于强度时，不会发生失效；当应力大于强度时，就会发生失效。设应力为X，强度为Y。X与Y都应为服从某分布的随机变量。那么可靠度R就应为Y>X的概率，即R=P（Y>X）=P（Y-X>0）。

应力-强度干涉模型是机械产品可靠性设计的基础，但由于实际应用到的数据往往不是两个，而是包括应力、强度、载荷、尺寸等的n维随机向量。因此需要把应力-强度干涉模型推广到n个随机变量的一般情况。

令Z=Y-X=G（x1，x2，…xn），则R=P（Z>0）=P（G（x1，x2，…xn）>0）。其中G称为功能函数。设第i个变量的均值为μi，标准差为σi，对于G为线性函数的情形，可以推导出R=Φ（β），β=称为可靠度系数，Φ为标准正态函数。而当G不是线性函数时，可以将G在某设计点P（x1*，x2*，…xn*）进行泰勒展开，略去高阶项，化为线性函数，称为一次二阶矩法。可以产出，一次二阶矩法的核心在于确定设计点P。一旦确定了设计点，就可以按R=R=Φ（β）进行计算。

如果将设计点取为均值点，称之为均值点法或中心点法。但由于对非线性函数G，均值点不在失效曲面G=0上，使得误差增大。解决办法是在失效曲面上取离均值点最近的点作为设计点，这种改进的一次二阶矩法叫做验算点法，其主要步骤如下。

（1）给各随机变量赋初值x*=（μ1，μ2，…，μn）。

（2）计算功能函数在各随机变量当前取值点的偏微分。

（3）计算灵敏度系数。

（4）计算功能函数在各随机变量当前取值点的可靠度系数β。

（5）利用求得的β计算x*的新值。

重复步骤（2）至步骤（5），直到所得β值与上一次的β值之差小于容许误差。此时所求得x*=（x1*，x2*，…xn*）即为设计点，可靠度R=Φ（β）。

2 应力场强度因子断裂理论

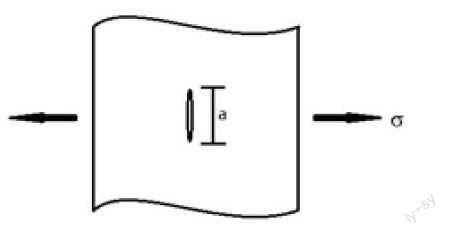
无限大平板上有一长为a的微小裂纹，两边受拉伸载荷，板内分布应力为σ。求结构的失效概率（裂纹发生扩展概率）。

其中断裂韧性KIC均值取2 000 MPa·mm1/2，结构内拉应力σ的均值取300 MPa，裂纹尺寸a的均值取4 mm，各随机变量的变异系数分别取0.1和0.15。计算控制精度ε取0.001。

对随机变量取不同的变异系数组合，其相应的可靠度系数β和失效概率Pf如表1所示。

从表中可以看出，对于含有一表面裂纹的焊接结构，当不考虑焊接残余应力时，断裂韧性、应力、裂纹尺寸3个随机变量的变异系数均为0.1时，结构的失效概率为3.300e-5，表明结构仍然具有较高的可靠性。在3个随机变量中，断裂韧性KIC的变异对结构的可靠性影响最大，其次是应力σ，裂纹尺寸a的变异对结构的可靠性的影响远比KIC和σ小。

在结构含有一定数值的残余应力时，首先应该控制看疯金属KIC的变异系数，即提高焊缝金属的冶金质量，尽量使其波动减小；其次应该控制载荷的变异；就裂纹尺寸而言，在无损检测时适当的误差范围并不会对结构的可靠性引起很大的影响。

4 结论

（1）该文介绍了应力—强度干涉模型，以及基于此的一次二阶矩算法。

（2）自行编写了计算程序，用该程序对含缺陷焊接结构的可靠度系数和失效概率进行了计算。

（3）结果表明，断裂韧性KIC，应力σ和裂纹尺寸a三个随机变量中，KIC的变异对结构可靠性影响最大，σ的变异影响其次，a的变异对可靠性的影响较前两者都小。

（4）该文介绍了基于应力-强度干涉模型的含缺陷焊接结构可靠性的计算方法，为含缺陷焊接结构的可靠性分析开辟了新的途径。

参考文献

[1] 李良巧.可靠性工程师手册[M].北京：中国人民大学出版社，2012.

[2] 何柏林，霍立兴，张玉凤，等.基于三维随机有限元法的含缺陷焊接结果可靠性分析[J].机械强度，2000（22）：291-293.

[3] 傅积和，孙玉林.焊接数据资料手册[M].北京：机械工业出版社，1994.