如何高效利用习题变式
裴树峰 杨国辉
在数学中考复习中,切实提高复习的效率,夯实学生的基础,培养学习数学的方法,提升综合运用知识能力,是我们面临中考前必须具备的各项本领.所以,在中考复习中要注重教材的知识内容,领悟教材的精髓,挖掘典例习题的精华思想,延伸思维,争取收到事半功倍的效果.下面以2013年人教版教材的一道经典习题为例,与同学们一起交流有关中考复习的体会.
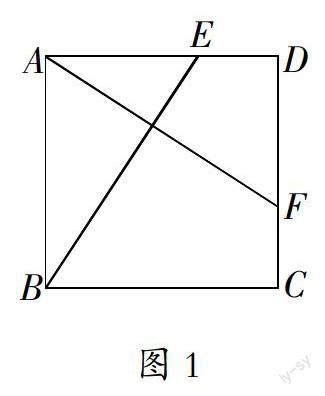
例1:(人教版数学教材八年级下册第68页综合运用中的第8题)如图1,ABCD是一个正方形花园,E、F是它的两个门,且DE=CF,要修建两条路BE和AF,这两条路等长吗?它们有什么数量关系?为什么?
解答:两条路等长,相等.
理由:如图1,因为在正方形ABCD中,所以AB=AD.因为DE=CF,所以AE=DF.又因为正方形ABCD,所以∠ADC=∠BAD=90°.所以△ABE≌△DAF,所以AF=BE.
本题的考点是正方形的性质和全等三角形的性质.这些考点在最近两年的各省市中考命题里应用是比较多的,本道题的关键是将正方形的性质和全等三角形的性质的知识应用于生活实际中.通过解答这道题我们要学会在审题的过程中进行思维转化,快速抓住题目所给的有效信息.具体方法如下:
一、由静态到动态,培养数学的运动变化思维
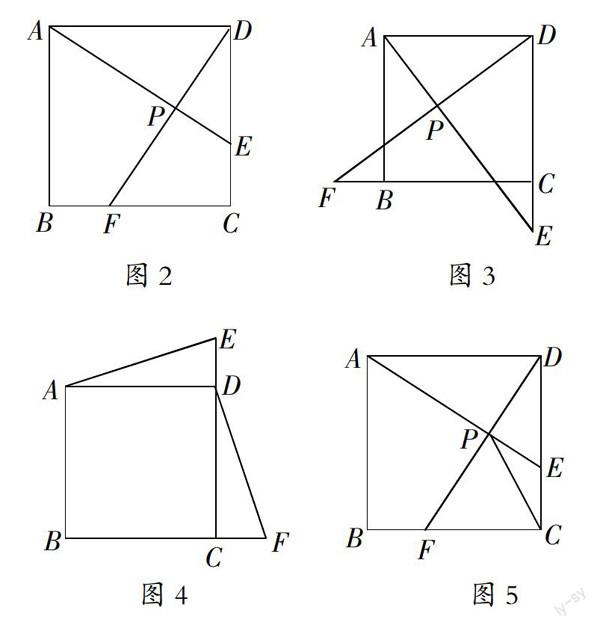
例2:在正方形ABCD中,动点E、F分别从D、C两点同时出发,以相同的速度在直线DC,CB上移动。
(1)如图2,当点E自D向C,点F自C向B移动时,连接AE和DF交于点P,请你写出AE与DF的位置关系,并说明理由;
(2)如图3,当E、F分别移动到边DC、CB的延长线上时,连接AE和DF,(1)中的结论还成立吗?(请你直接回答“是”或“否”,不需证明)
(3)如图4,当E、F分别在边CD、BC的延长线上移动时,连接AE、DF,(1)中的结论还成立吗?请说明理由;
(4)如图5,当E、F分别在边DC、CB上移动时,连接AE和DF交于点P,由于点E、F的移动,使得点P也随之运动,请你画出点P运动路径的草图.若AD=2,试求出线段CP的最小值.
解答:(1)AE=DF,AE⊥DF.先证得△ADE≌△DCF.由全等三角形的性质得AE=DF,∠DAE=∠CDF,再由等角的余角相等可得AE⊥DF.
(2)成立.四边形ABCD是正方形,所以AD=DC,∠ADE=∠DCF=90°,DE=CF,所以△ADE≌△DCF,所以AE=DF,∠DAE=∠CDF,因为∠CDF+∠ADF=90°,∠DAE+∠ADF=90°,即AE⊥DF.
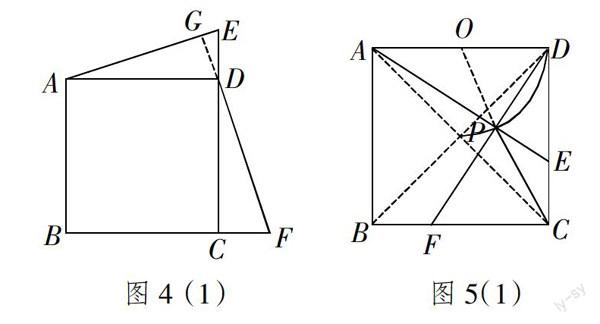
(3)成立.由(1)同理可证AE=DF,∠DAE=∠CDF,延长FD交AE于点G如图4(1),再由等角的余角相等可得AE⊥DF.
(4)由于点P在运动中保持∠APD=90°如图5
(1),所以点P的路径是一段以AD为直径的弧,设AD的中点为O,连接OC交弧于点P,此时CP的长度最小,再由勾股定理可得OC的长,再求CP即可.
本题的关键是将原来教材中重点的题变式演化而命制.属于几何图形变换题型.此类型题的主要解题方法是抓住几何图形的变换特征,学会应用运动变化的角度解决问题,由静态到动态,千万别被“动”吓到,其实它并不难.如题目中的“动点E,F分别从D,C两点同时出发以相同的速度在直线DC,CB上移动”这关键的“题眼”,便明确了动点的运动路径的不同情况,这种题型在近几年的中考命题中考查比例很大.通过本题的训练,重点学会以下几点方法:
1.对教材的典型例题、习题进行多角度地变式,特别是变换图形的条件、位置,进而培养灵活变化的思维.
2.通过探究几何图形的变换过程中的蕴藏的规律,让自己真正体会几何图形的运动变化中的一静一动的内在变化关系,切身经历知识规律的探究过程,感受学习数学的快乐.
二、从特殊到一般,培养猜想探究问题的能力
例3:九年级数学兴趣小组在学校的“数学长廊”中兴奋地展示了他们小组探究发现的结果,内容如下:
(1)如图6,正三角形ABC中,在AB、AC边上分别取点M、N,使BM=AN,连接BN、CM,发现BN=CM,且∠NOC=60°.
请证明:∠NOC=60°.
(2)如图7,正方形ABCD中,在AB、BC边上分别取点M、N,使AM=BN,连接AN、DM,那么AN= ,且∠DON= 度.
(3)如图8,正五边形ABCDE中,在AB、BC边上分别取点M、N,使AM=BN,连接AN、EM,那么AN= ,且∠NOE= 度.
解题过程:
(1)根据已知条件可以证明△ABN≌△BCM,得∠ABN=∠BCM,进而得到∠NOC=60°;
(2)先证明△ABN≌△DAM,得AN=DM,∠ADM=∠BAN,最后得∠DON=90°.
(3)先证明△ABN≌△EAM,得AN=ME,再得∠AEM=∠BAN,最后得∠NOE=∠NAE+∠AEM=∠NAE+∠BAN=∠BAE=108°.
本题的考点是等边三角形的性质、全等三角形的判定和性质、正多边形的性质等知识.这些知识都是近几年中考命题的重点.本题的关键是“正三角形、正方形、正五边形……至正多边形”的特殊到一般的数学思想的体现.增强了对几何图形的特殊到一般的探究猜想的 应用意识和能力.通过本题应该掌握“一个方法、一种思想”:
1.一个方法:变换图形的形状、拓展几何图形的宽度(横向变化、纵向变化),是我们学习数学最常用的变式训练的另一种方法。从中感受到几何图形的“动中有变,变中不变”,提高自己的思维探究意识.
2.一种思想:从特殊到一般的数学思想方法.对公式、定理、法则的学习往往都是从特殊开始,通过总结归纳得出来的,证明后,又使用它们来解决相关的数学问题.分析历年的中考试题,考查特殊与一般的思想的题比比皆是,所以这类题型必然成为今后中考命题改革的方向,希望引起高度重视.
三、变式几何题目背景,培养综合应用能力
例4:正方形ABCD在如图9所示的平面直角坐标系中,A在x轴正半轴上,D在y轴的负半轴上,AB交y轴正半轴于E,BC交x轴负半轴于F,OE=1,抛物线y=ax2+bx-4过A、D、F三点.
(1)求抛物线的解析式;
(3)在射线DB上是否存在动点P,在射线CB上是否存在动点H,使得AP⊥PH且AP=PH,若存在,请给予严格证明,若不存在,请说明理由.
解题过程:
(1)根据△OEA∽△ADO,D(0,-4),E(0,1)可求出A点的坐标,再根据Rt△ADE≌Rt△ABF可求出F点的坐标,把A,F两点的坐标代入二次函数的解析式即可得出未知数的值,进而求出其解析式;
(3)先根据题意画出图形,根据图形可看出,有三种情况符合题目条件:
图①通过证明Rt△PQH≌Rt△ANP得到∠APN+∠HPQ=90°,进一步得到AP⊥PH,
图②通过证明Rt△PMH≌Rt△PAN和PN∥BH得到∠HPA=∠NPA+∠HPN=∠MHP+∠HPM=90°,
图③通过证明Rt△PNH≌Rt△PMA和PN∥AB,得到∠HPA=90°.
本题的考点是三角形相似的性质、全等三角形的性质、二次函数解析式等知识.本题的难点是将教材中的原来的典型习题经过新加工变式,变换了几何图形的新背景,将二次函数与几何图形的有机结合,使原来题目增加了难度和挑战性,这势必将成为将来中考命题的方向和趋势.因此,强烈建议同学们在平时的学习过程中,一定要多从基础知识基本技能着手,以基本的问题为着眼点,夯实基础知识,学会积极探究、发现分析解决问题的方法,进而提升学习的能力,一定会提高我们的数学成绩.
同学们,近几年的中考命题一直推崇“源于课本,回归课本,在教材中能找到中考题目的影子”的命题理念.所以在日常学习中,一定要认真学习教材,从而实现由注重知识过渡到注重能力.学会回归教材,以便使我们在题海中把自己解救出来,在中考复习期间收获颇丰,使中考数学成绩得以提高.

