电缆电气参数不同计算方法及其比较
蒋彦波 史记 蒋彦韬

摘要:电缆电气参数的计算一直都是人们所研究的重要问题。在具体计算过程中,为了能够更加简单、直观、方便地完成对电缆电气参数的计算,针对不同的电缆电气参数算法进行了对比与介绍,通过对比找出最佳的算法供人们使用,从而使工程施工变得更加简单。
关键词:电缆电气;计算方法;参数计算;工程施工;联网;供电 文献标识码:A
中图分类号:TM246 文章编号:1009-2374(2016)20-0072-02 DOI:10.13535/j.cnki.11-4406/n.2016.20.035
进入21世纪后,全球经济和科技都得到了飞速发展,并且随着人们环保意识的提高,新能源的应用得到了进一步推广。目前,联网和供电是人们生活中不可或缺的两部分,而联网与供电二者在具体实施过程中,都需要以电缆作为载体。同时,电缆具有占地面积小、可靠性高、搭设简单、信息传输快等多项优点,因此在许多领域都得到了广泛的应用。在应用电缆过程中,要做好电气参数计算与分析,这对电缆的应用有着重要影响。
1 各种电缆电气参数算法介绍
1.1 方法一
对电缆在应用过程中,利用多导体对构建电缆的电路模型进行科学分析,如果在电缆的实际应用过程中,没有铠装层存在,那么在实际操作中,本应当由3根单芯电缆所构成的输电线路,则会包含6根导体以及与大体进行连接。需要注意的是,这6根导致相互之间要保护平行,同时每根导体要与地面保持平行。阻抗矩阵型的计算原理如下:如果在分析过程中dij≤0.135DcA,在具体计算过程中则可以对Carson-Clem公式进行应用,弯沉对电缆阻抗矩阵的计算,单位为Ω/km。
在式(1)和式(2)中,ri表示的为单位导体内电阻值的大小,在具体计算过程中,需要对邻近效应和集肤效应进行充分考虑,如果再对导体进行分割处理,那么在具体操作过程中,如果对导体进行上漆处理,可以有效地降低各种效应的发生情况。通常来说,在上述公式中的DCA=660,这也被称“Carson深度”,而在这个小公式中,表示土壤的电阻率的,单位为Ω·m;表示频率,单位为Hz;dij表示两个相邻导体之间的距离,单位为m。
1.2 方法二
电缆电气参数的计算也可以通过Matlab中的power cableparam功能完成,通过相关图形用户界输入相应的参数,从而获得电缆的ELC矩阵。下面针对power cableparam电缆参数的计算方法进行重点介绍:
在式(3)中,RC(dc)表示通过导体的直流电阻;RC(E)表示导体的大地的回流电阻值,通过实际测量可知,该数值的大小为π2×104f,单位为Ω/km;
k1=0.0529f/(3.048×60),表示频率因数,单位为Ω/km;De=1650为导体是等效大体回路的距离,单位为m;GMR表示导体的几何半径大小,单位为m。
在计算过程中线芯之间的阻抗计算如式(4)所示:
式(4)中的GMD表示相邻导体之间几何的平均距离,其中n表示所有导体间距的总数,通常来说,并不需要利用此公式完成对GMD的计算,而是作为输入参数直接获取。
护套自阻抗的计算通过式(5)完成:
在式(5)中,Dn表示内绝缘层和相导体平均半径之间的距离大小,单位为m。
护套间与线芯之间的电阻为:CCS=。在上述公式中,假定是XLPE绝缘层,εCS表示内绝缘层的相对介电常数;dia、doa分别表示内绝缘层和外绝缘层半径的大小,单位为m。
1.3 方法三
交流电阻计算,在电缆中导体与护套之间电阻的计算应当依据式(6)进行计算。
在式(6)中,R(ac)以及R(dc)表示的为电缆导体,后者为护套中的交流电或直流电,电阻值的大小,单位为Ω。在具体计算过程中,对于三芯、双芯、单芯不同类型的电缆来说,y值都应当取1。如果电缆属于管道类型,y的取值将会有所变化,通常应当为标准取值的1.5倍,因为常规取值为1,因此在管道电缆中,y的取值应当为1.5。在式(6)中,ks表示集肤效应系数,而kp表示相邻近效应系数。在具体计算过程中,电路中直流电阻的计算如式(7)所示:
在式(7)中,ρ表示整条电力电阻率的大小,单位为Ω·m;A表示电缆导体标截面面积的大小,单位为m2;θ表示电缆运行过程中,电缆的温度,单位为℃。
2 三种方法的计算结果与对比
对电缆电气参数的三种计算方法进行了详细介绍,下面采用不同方法进行计算,获取的电感、电阻、电容部分参数,在具体操作过程中,电缆的排列方式的种类有很多,主要针对带铠装电缆和不带铠装电缆两种情况进行下,1根三芯电缆或3根单芯电缆程等边三角形的排列的情况机型对比分析。
2.1 没有铠装层电缆
没有铠装层电缆呈等边三角形排列时,3根电缆之间距离完全相同,表1为3种不同计算方法下,得到的电阻矩阵中的部分参数;表2中表示的则为电感矩阵中的部分参数,在表中,C表示导体,S表示护套,下脚标表示导体的具体编号,例如S2C1表示为2号电缆的护套与1号电缆导体之间的互电感或互电阻。电缆电容的矩阵参数详细信息如表3所示:
通过表1、表2、表3将各项参数输入,然后依据阻抗推导公式,对没有铠装的等边三角形序列的阻抗进行计算,通过计算结果可知,正序阻抗和负序阻抗两者的数值相等,并且在正序电感和零序电感达到一定频率后,两者的数值趋近相等,但是如果在具体电缆铺设过程中,电缆为平铺,正序电感和零序电感的频率范围将会存在较大差距。
2.2 铠装电缆
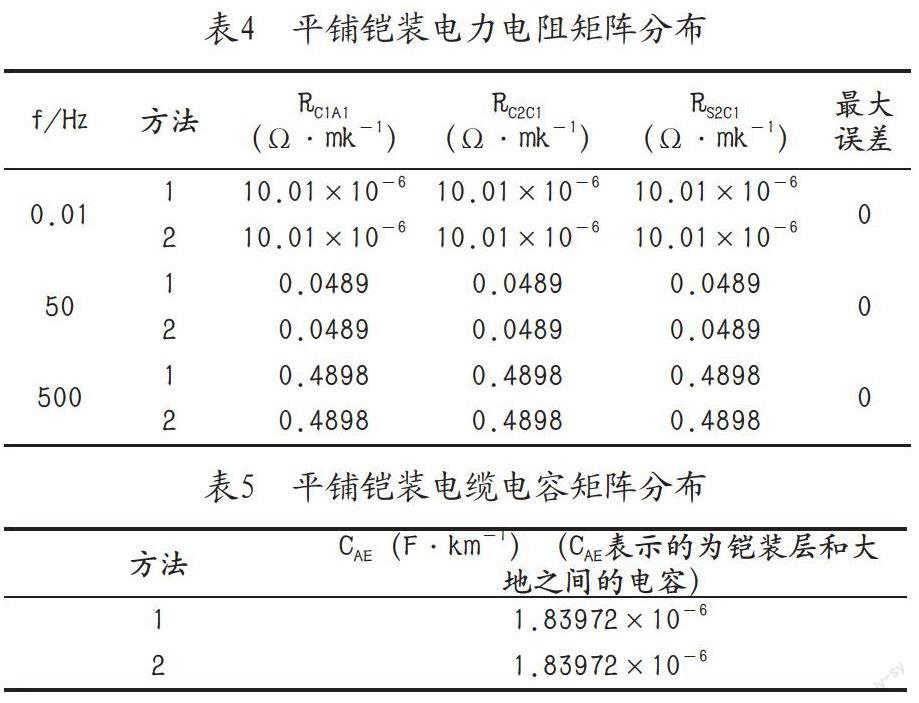
在对铠装电缆进行分析时,假设铠装层的材料为铝,开组层的内径大小为0.0689m,外径的大小为0.07988m,电阻率的大小为3×10-8m,对电缆的横截面积进行量测,通过量测得到电缆横截面积大小为0.0028m2,电缆的相对磁导率大小为1.5,电缆外层的橡胶互层的厚度为0.003m,相对介质常数大小为2.5。其余参数,例如护套、线芯等,都与没有铠装电缆的参数相同。表4、表5分别对比了方法二和方法三两种计算方法所获得的电阻、电容参数,这主要因为power cablepram算法不能用于对没有铠装电缆参数的计算。
3 结语
综上所述,电缆电气参数计算过程中可以采用不同的方法进行,不同的计算方法取得的效果不同。本文主要分析了三种不同的计算方法,从电缆电气参数计算的准确性和便捷性来看,在计算中应用方法一是最佳选择。
参考文献
[1] 甘启才.电力电缆电气参数及电气特性研究[J].中国高新技术企业,2016,(3).
[2] 李婧,郭金明,黄锋.用于电力电缆现场测试的电气参数及接头位置识别装置的研制[J].低碳世界,2015,(31).
[3] 杜伯学,李忠磊,张锴,王立.220kV交联聚乙烯电力电缆接地电流的计算与应用[J].高电压技术,2013,(5).
[4] 郑雁翎,王宁,李洪杰,张冠军.电力电缆载流量计算的方法与发展[J].电气应用,2010,(3).
[5] 成凌飞,王泰华.矿用通信电缆基本电气参数数值模型[J].电工技术学报,2010,(12).
[6] 唐忠,高巍.单芯XLPE电缆分布参数的研究与计算
[J].华东电力,2014,(3).

