小学分数应用题教学之我见

陈元翠

应用题的教学是小学数学教学的重点教学内容之一，也是难点之一，特别是分数应用题，更是小学六年级的重点教学内容。在教学中教师怎样突破难点，解决重点，让学生在轻松愉快的氛围中既学到解决问题的方法，又培养了学生的思维能力。这就要求老师处理好教材，真正把握和应用好教材，让学生真正掌握解答分数应用题的解题规律，那么在小学分数应用题教学中如何培养学生思维能力，发掘其解题奥妙，并能让学生乐在其中，这就成了我们小学数学教师研究的一个重要课题。

一、找准单位“1”分析数量关系

应用题最关键的一步找准单位“1”是解答应用题分数，分数应用题其关系错综复杂，条件千变万化，比如：苹果个数是梨的单位“1”容易找到，梨是单位“1”换一种说法，梨的是苹果的个数，怎么找到单位“1”，犯难了，学生往容易找错，这样做问题解决了，即谁的，梨的，那么，梨就是单位“1”，就不会找成苹果是单位“1”了，再通过反复类似的训练，学生就会很容易的找出题中的单位“1”。又比如：苹果比梨少，找单位“1”也是一个难点，老师的引导很重要：苹果少谁的，少梨的，反复地说、读，学生就会明白，梨是单位“1”。找准单位“1”这是第一步，也非常重要。因为单位“1”找错了，整个解决题思路就全部错了，所以非常关键。另外，找单位“1”快捷方法：找题中的关键词，比、占、关于、相当于是，后面那个量就是单位“1”。

二、使用线段图分析数量关系

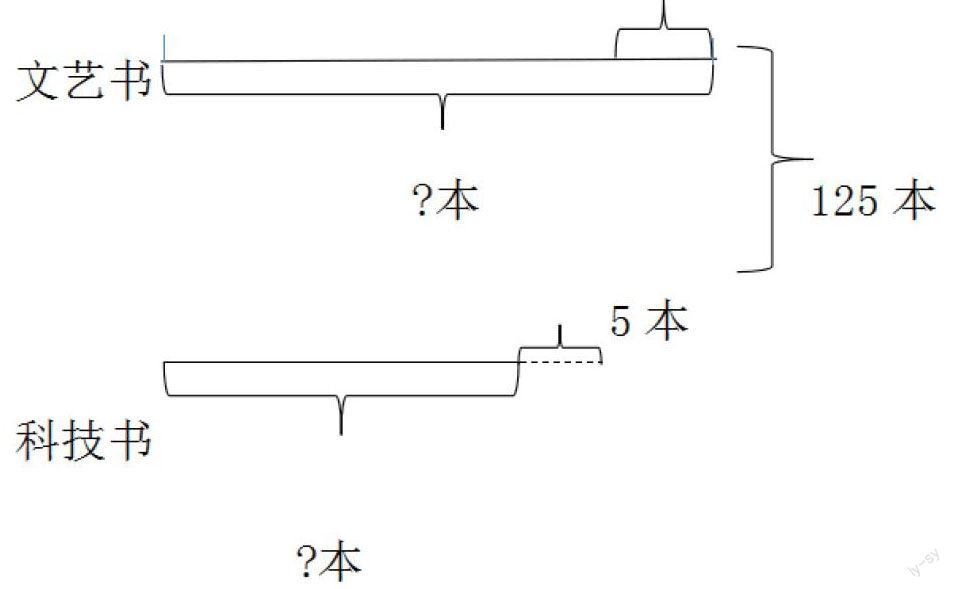
借助线段图，能讲稍复杂抽象难理解的分数应用题问题简单化，就能理解有关数量与单位“1”的对应关系。比如：阅览室有文艺书和科教书共125本，如果文艺书借出，比科技书还多5本。原来文艺书和科技书各有多少本？

思路：假设科技书增加5本，就与文艺书借出后剩下的本数一样多。如下图所示：

观察图后不难理解：科技书增加5本后，科技书的本数是文艺书的，两种书的总本数为125+5=130（本），可得文艺书的本数为130÷（1+）=70（本），科技书的本数为125-70=55（本）。

文艺书的本数：（125+5）÷[1+（1-）]=70（本）

科技书的本数：125-70=55（本）

答：原来文艺书有70本，科技书有55本。

三、转化单位“1”找准量与率

在教学实践中，我注重学生的思维训练，对分数应用题中单位“1”的转换也进行了一些尝试和探索。如：数学课外兴趣小组中，上学期男生占5/9，这学期增加21名女生之后，男生就只占了2/5，这个小组现有女生多少人？此题看起来单位“1”都是兴趣小组总人数男生占5/9，然而总人数发生了变化，因为增加了女生，随之总人数也跟着增加了，所以不能把总人数看做单位“1”来确定量与率，男生人数不变，所以可将男生人数确定为单位“1”，于是，男生占5/9，可转化成原兴趣小组人数占男生的9/5，男生占2/5，可转化成现在兴趣小组人数占男生的5/2，量21对应的分率则是（5/2-9/5），那么男生人数是：21÷（）=21x10/7=30人，现在的女生：30÷2/5-30=45人。再如：有甲、乙两筐梨，乙筐梨的质量是甲筐梨的质量的3/5，从甲筐取出5千克梨放入乙筐后，乙筐的梨的质量是甲筐梨的质量的7/9，甲、乙两筐梨的总质量是多少千克？

思路：由于题中两筐梨的总质量没有变，我们把两筐梨的总质量看作单位“1”则原来甲筐梨的质量占总质量的，后来甲筐梨的质量占总质量的，所以，5千克梨相当于总质量的，即5÷（）=80（千克）。

四、抓不变量，解决问题

逐步变亮，解分数应用题，是常见的解答分数应用题的方法之一，其关键是在众多复杂的描述中怎样才能找出其中的不变量，所以在教学中找差不变、和不变是很常见的。如：某学校原有长跳绳的根数占长、短跳绳的3/8，后来又买了进20根长跳绳，这时长跳绳的根数占长、短跳绳总数的7/12，这个学校现有长、短跳绳的总数是多少根？

思路：

解法一：我们应特别注意题中“3/8”与“7/12”这两个分数的单位“1”不相同。根据短跳绳的根数没有变，我们把短跳绳的根数看作单位“1”，可以得出原来长跳绳根数与短跳绳的，后来的长跳绳根数是短跳绳根数的，这样就找到20根长跳绳相当于短跳绳的，从而求出短跳绳的根数。在用短跳绳的根数除以（1-7/12）就可求出这个学校现有跳绳的总数。即（根）。

解法二：把短跳绳的根数看作单位“1”，原来的总数是短跳绳的，后来的总数是短跳绳的。所以20÷=60（根）。

总之，要想正确解答分数应用题，就必须要掌握分数应用题的规律。熟知分数应用题的数量关系。掌握分数应用题中的对应量和分率的对应规律，熟练进行分率转换。这样就能正确分析和理解千变万化，错综复杂的数量关系从而提高解题能力。在实施素质教育的今天，让学生乐学，学得轻松。如何让学生在应用题这个乐园中露出天真的笑容是我一直努力的方向。我将努力落实课标精神，通过学生自主探索，让学生创造数学，应用数学，从而让学生成为数学学习的主人。

（作者单位：攀枝花市米易县第一小学校）