纤维增强复合材料力学模型研究进展

胡翠平　夏玉峰　张绪涛

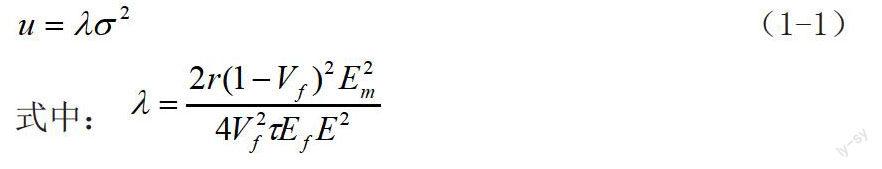
摘 要：本文介绍了多种研究纤维增强复合材料损伤和破坏的力学模型，对各模型从提出到发展进行了介绍和分析，说明了各模型的特点。最后，对其研究意义进行了总结。

关键词：纤维增强复合材料；损伤；破坏；模型

纤维增强复合材料的力学研究起始于本世纪五十年代，伴随着玻璃纤维增强聚脂材料（玻璃钢）以及其他硼纤维，碳纤维和芳纶纤维在工程中的大量应用而迅速发展起来。为了研究复合材料破坏机理及强度，国内外学者提出了很多纤维增强复合材料损伤和破坏模型。

1 纤维增强复合材料力学模型

1.1 剪滞模型

Cox于1952年提出了剪滞模型，该模型是分析纤维增强复合材料强度和损伤最常用方法之一。Hedgepeth首次将剪滞模型应用于多纤维系统。Wagner等曾用剪滞模型研究从一根纤维失效到与其相邻纤维应力重分布问题。

用Monte-Carlo理论和剪滞模型，Beyerlein等研究了纤维强度统计学对断裂过程的影响。Landis等提出了三维剪滞模型，又把它与纤维纬布统计和影响叠加原理结合，应用于分析复合材料强度统计分布和尺寸效应的影响。

Li等影响叠加原理同有限元模型结合起来，模拟了在纤维增强聚合物复合材料中从破坏纤维到未破坏纤维的应力传递。Xia等采用三维有限元微观力学研究了纤维增强复合材料的变形及应力传递。Xia等比较了复合材料中应力传递的剪滞模型和三维有限元微观力学模型，得出剪滞模型适用于纤维/基体的高刚度比和纤维体积含量高的情况，而不适于纤维体积含量低的情况。

1.2 纤维束模型及其变型

最初的纤维束模型是由Daniels（1945）提出的，该模型假定整体承担荷载。Zhou等指出，该模型仅仅适用于没有基体的松散的纤维束模型。Harlow等提出局部承担荷载模型，在此模型中，本来由失效纤维（束）承担的荷载转移到由与其相邻的两纤维（束）承担。Curtin指出，在GLS条件下的独立且连续纤维的断裂问题已经简化为基体中单根纤维的破坏问题。

Kun等提出了蠕变断裂和界面失效的连续损坏纤维束模型，研究了复合材料的定比特性，并观测到脆性纤维的破坏可以使复合材料具有延性特征。

1.3 裂缝桥联模型

对于陶瓷和其他脆性基体复合材料，裂缝桥联纤维使材料韧性提高的问题很重要，纤维和基体的粘结决定了复合材料的抗裂性能。Aveston等提出了典型的基于断裂力学的基体断裂模型，假设纤维只受摩擦力的情况下，分析了由于基体开裂引起陶瓷基体复合材料中能量的转换问题，得到了复合材料中基体的破坏条件。

Budiansky等考虑了复合材料中基体裂缝的稳定扩展，考虑到由于裂缝扩展导致的摩擦能量和势能改变等因素，并根据能量守恒，确定了未粘结（靠摩擦力约束，滑落）和纤维最初粘结后来分离的复合材料中的基体开裂应力。用剪滞模型和连续分布的非线性弹簧模型，Budiansky等确定了完整的和脱粘的纤维桥联的基体中的应力，并推导出一等效的裂缝桥联定律，这个定律考虑了脱粘韧性和摩擦滑动的影响。Zok等研究了有多条基体裂纹的延性基体复合材料的变形。Zok等对一恒定界面抗滑应力，裂缝断距u可由桥接应力的函数被确定：

E—复合材料的杨氏模量，r—纤维半径，下标f和m分别代表纤维和基体。

Gonzalez-Chi等采用了Piggott提出的局部脱粘理论来分析裂缝桥联问题，在这个理论体系中，以剪滞模型为基础，并被发展分析纤维拔拉实验。在变形区域，纤维/基体界面被看作是由一系列的脱粘区域组成，此时应力随纤维长度呈线性变化。

2 总结

综上所述，近五十年来对纤维增强复合材料力学模型的研究经历了很大飞跃，前人作了大量的研究，并不断超越，模型的不断完善和创新推动了纤维增强的破坏机理和强度预测的深入研究，确保了其使用的可靠性和科学性，具有重要研究价值和应用前景。

参考文献

[1]Wagner，H.D.，Eitan，A.，Stress concentration factors in two-dimensional composites - Effects of material and geometrical parameters[J].Composites Science and Technology，1993，46（4）：353-362.

[2]Beyerlein I.J.，and Phoenix S.L.，Sastry A.M.，Comparison of shear-lag theory and continuum fracture mechanics for modeling fiber and matrix stresses in an elastic cracked composite lamina[J].Int J Solids and Structures，1996，33（18）：2543-2574.

[3]Landis C.M.，Beyerlein I.J.and McMeeking R.M.，Micromechanical simulation of the failure of fiber reinforced composites[J].J Mechanics and Physics of Solids，2000，48（3）：621-648.

[4]Li H.，Jia J.X.，Geni M，Wei J and An L.J.，Stress transfer and damage evolution simulations of fiberreinforced polymer-matrix composites[J].Materials Science and Engineering：A，2006，（425）：1-2，178-184.

[5]Xia Z.H.and Curtin W.A.，Multiscale modeling of damage and failure in aluminum-matrix composite[J].Composites Science and Technology，2001，61，15，2247-2257.

[6]Xia Z.，Curtin W.A.and Okabe T.，Greens function vs.shear-lag models of damage and failure in fiber composites[J].Composites Science and Technology，2002，（62）：10-11，1279-1288.

[7]Daniels，H.E.，The statistical theory of the strength of bundles of threads，Proc[J].Royal Society London，1945，（A183）：405.

[8]Zhou X.-F.，Wagner H.D.Stress concentrations caused by fiber failure in two-dimensional composites[J].Composites Science and Technology，1999，（59）：1063-1071.

[9]Harlow，D.G.，and Phoenix，S.L.，Chain-of-Bundles Probability Model for Strength of Fibrous Materials [J].1.Analysis and Conjectures，J.Compos.Mater.，1978，（12）：195-214.

[10]Curtin W.A.，Theory of Mechanical Properties of Ceramic-Matrix Composites[J].Journal of the American Ceramic Society，1991，74（11）：2837-2845.

[11]Budiansky，J.W.Hutchinson and A.G.Evans，Matrix fracture in fiber-reinforced ceramics.，Journal of Mechanics and Physics of Solids，1986，34（2）：167-189.

[12]Budiansky B.，Evans A.G.，Hutchinson J.W.Fiber-matrix debonding effects on cracking in aligned fiber ceramic composites[J].International Journal of Solids and Structures，1995，32（3）：315-328.

[13]F.W.Zok，M.R.Begley，T.E.Steyer and D.P.，Walls Inelastic deformation of fiber composites containing bridged cracks[J].Mechanics of Materials，1997，26（2）：81-92.

[14]González-Chi P.I.and R.J.Young，Crack bridging and fibre pull-out in polyethylene fibre reinforced epoxy resins[J].Materials Science，1998，33（24）：5715-5729.

（作者单位：青岛工学院）