基于不同前角的航空铝合金切削过程分析*

秦 宇，沙智华，刘 宇

（大连交通大学机械工程学院，大连 116028）

铝合金7050-T7451（以下简称7050）为Al-Zn-Mg- Cu系合金，属于7系列铝合金的一种，具有高强度、高韧性以及高的抗应力腐蚀性能，是航空航天器轻量化广泛采用的一种结构材料[1]。7050的塑性相对较低，多采用高速切削加工，刀具前角是影响其切削过程的重要参数。前角过大可能导致切削刃处产生弯曲应力造成崩刀，前角过小会增大前刀面与切屑间的摩擦力，加快刀具磨损。由此可知，深入了解前角变化对切削过程的影响，对提高生产率、降低生产成本、保证加工质量等方面具有指导意义。许多学者在这方面的研究主要考虑前角对切削力和切削温度的影响[2-4]，却很少重视前角对切屑形态的影响。切屑形态的好坏不仅影响已加工表面的质量，严重时还会危害操作者的人身安全和机床设备的正常运行。因此，本文以航空铝合金7050的切屑为研究对象，借助有限元软件ABAQUS/Explict，在研究切削力和切削温度的同时，着重于探究不同刀具前角条件下切屑形态的变化规律，为提高加工质量和生产率，降低生产成本，提供科学的依据和技术支撑。

1 前角对切削过程影响的理论分析

1.1 切削变形

切削变形程度可以用变形系数ξ和剪切角φ的大小来衡量，文献[5]给出了其理论计算公式

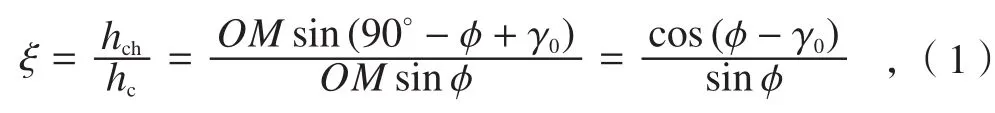
式中，ξ为变形系数，hch为切屑厚度，hc为切削层的厚度，OM为终滑移线，φ为剪切角，γ0为刀具前角。

从式1可以看出，前角γ0和剪切角φ是影响切削变形的两个主要因素，γ0和φ增大时，变形系数ξ减小，切削变形程度减小。

1.2 切削温度

切削温度一般指刀具前刀面与切屑接触面上的平均温度。车削加工时，切屑带走的切削热为50%～86%，刀具传出10%～40%，工件传出3%～9%，因此可从切屑方面考虑刀-屑接触面的平均温度，其表达式为[6]

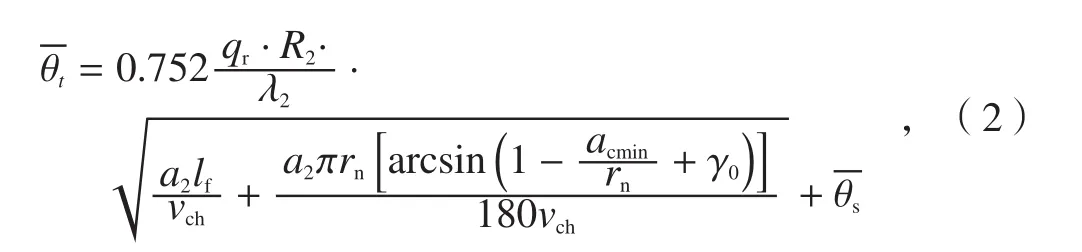
式中，qr为前刀面摩擦热源单位时间、单位面积产生的热量，R2为前刀面热量传入切屑的比例，λ2为导热系数，a2为导温系数，lf为前刀面和切屑的接触长度，vch为切屑速度，rn为刃口钝圆半径，acmin为极限切削厚度为剪切面的平均温度。

根据文献[6]，前角γ0增大时，切削宽度aw也随之增加，切削面积增大，切削温度降低。

1.3 切削力

在直角自由切削的条件下，作用在刀具上的力和作用在切屑上的力是一对作用力与反作用力。因此，可以将切屑上的力分解成沿着切削运动方向的主切削力Fc和垂直切削运动方向的切深抗力Fp，记作[5]

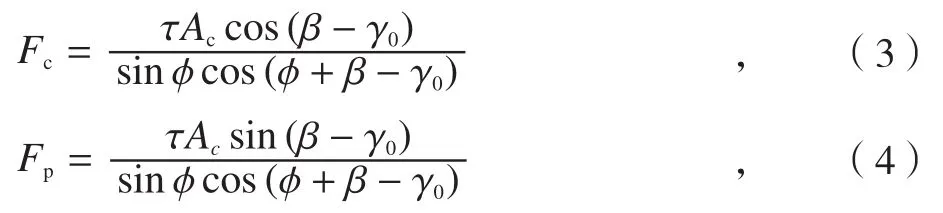
式中，τ是材料的剪切强度，Ac是切削层的截面积，β是摩擦角。

由式（3）、式（4）以及最大剪切应力理论可知，前角γ0增大，剪切角φ也随之增大，摩擦角β减小，主切削力Fc和切深抗力Fp均减小。

2 切削过程有限元模型的建立

2.1 几何模型和边界条件

在切削加工中，大多数切削属于三维切削，考虑到切削过程中切屑层的厚度远小于宽度，切屑在垂直切削刃各个截面上的应变状态、流经方向大致相同，可假设处于平面应变状态，因此可将复杂的三维切削简化为二维直角切削。所建立的正交切削有限元模型如图1所示，工件网格采用四节点平面应变热力耦合减缩积分单元（CPE4RT），在不降低仿真精度的同时，网格局部密划能缩短仿真时间。工件的底部和侧面施加全约束，刀具假定为刚体，限制y方向的自由度，以一定的切削速度从右向左运动。考虑到温度对整个切削过程的影响，工件和刀具的初始温度设为20℃。

图1 正交切削有限元模型Fig.1 Finite element model of orthogonal cutting

2.2 材料本构模型

金属切削过程是一个高度非线性的热-力耦合过程，材料在高温、大应变及高应变率的条件下发生弹塑性变形。材料本构关系反映了材料物质本性的变化,会对切削加工仿真结果的准确性产生根本影响。本文使用应用比较广泛、效果比较好的Johnson-Cook本构模型模拟工件的材料特性，该模型认为材料在大应变、高应变速率下表现为应变硬化、应变率硬化以及热软化效应[7]，能很好地描述材料的热粘塑性变形行为，其表达式为

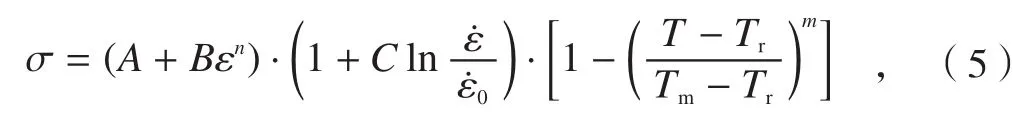
式中，A、B、n、C和m为材料参数，σ为等效应力，ε为等效塑性应变，为等效塑性应变率为参考应变率，Tr为参考温度，Tm为材料熔点。等号右边的3项分别反映了材料的应变强化效应、应变率敏感效应和温度敏感效应。通过分离式霍普金森压杆实验（SHPB）可以在实验数据相对较少的条件下获得Johnson-Cook模型的相关参数，文献[8]采用有限元迭代法优化本构方程参数，获得较高精度的7050材料参数如表1所示。

表1 7050 的Johnson-Cook本构方程参数

2.3 材料失效准则

ABAQUS/Explict中的Johnson-Cook模型提供了一个动态断裂失效模型来实现切屑与工件的分离[9]，该模型是基于单元积分点的等效塑性应变，适用于模拟高应变、高应变率的切削过程。Johnson-Cook模型定义的失效参数如下

式中为等效塑性应变增量，εpf为失效应变。当失效参数大于1时，则假定材料开始失效，若材料在所有积分点都失效，则网格中对应的单元会被删除。Johnson-Cook模型定义的失效应变为

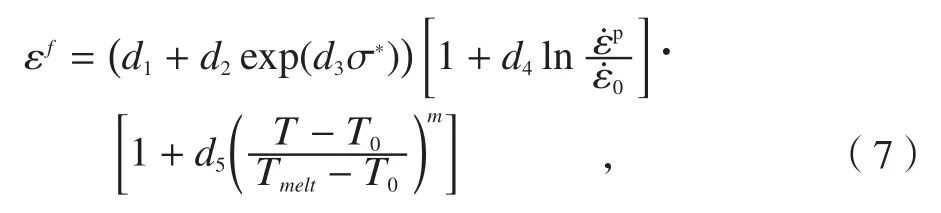
式中，d1～d5为失效参数，σ*为静水压应力与等效应力的比值， 为塑性应变率， 为参考应变率，T为当前温度，T0为参考温度，Tmelt为材料熔点。等号右边第一项表示断裂应变随着静水应力张量的增加而减小，第二项表示增加的应变率对失效应变的影响效应，第三项表示材料延性的热软化效应。d1～d5是在转变温度或低于转变温度的条件下，通过试件的高温拉压扭转实验获得的参数，文献[8]采用有限元迭代法对其进行修正，获得较高精度的7050失效参数如表2所示。

表2 7050的失效参数

3 前角对切削过程影响的有限元分析

在刀具后角为10°，切削速度为960m/min，切削深度为 0.2mm 的条件下，分别比较 -8°、0°、8°、16°前角对切屑形态、切削温度和切削力的影响。

3.1 刀具前角对切屑形态的影响

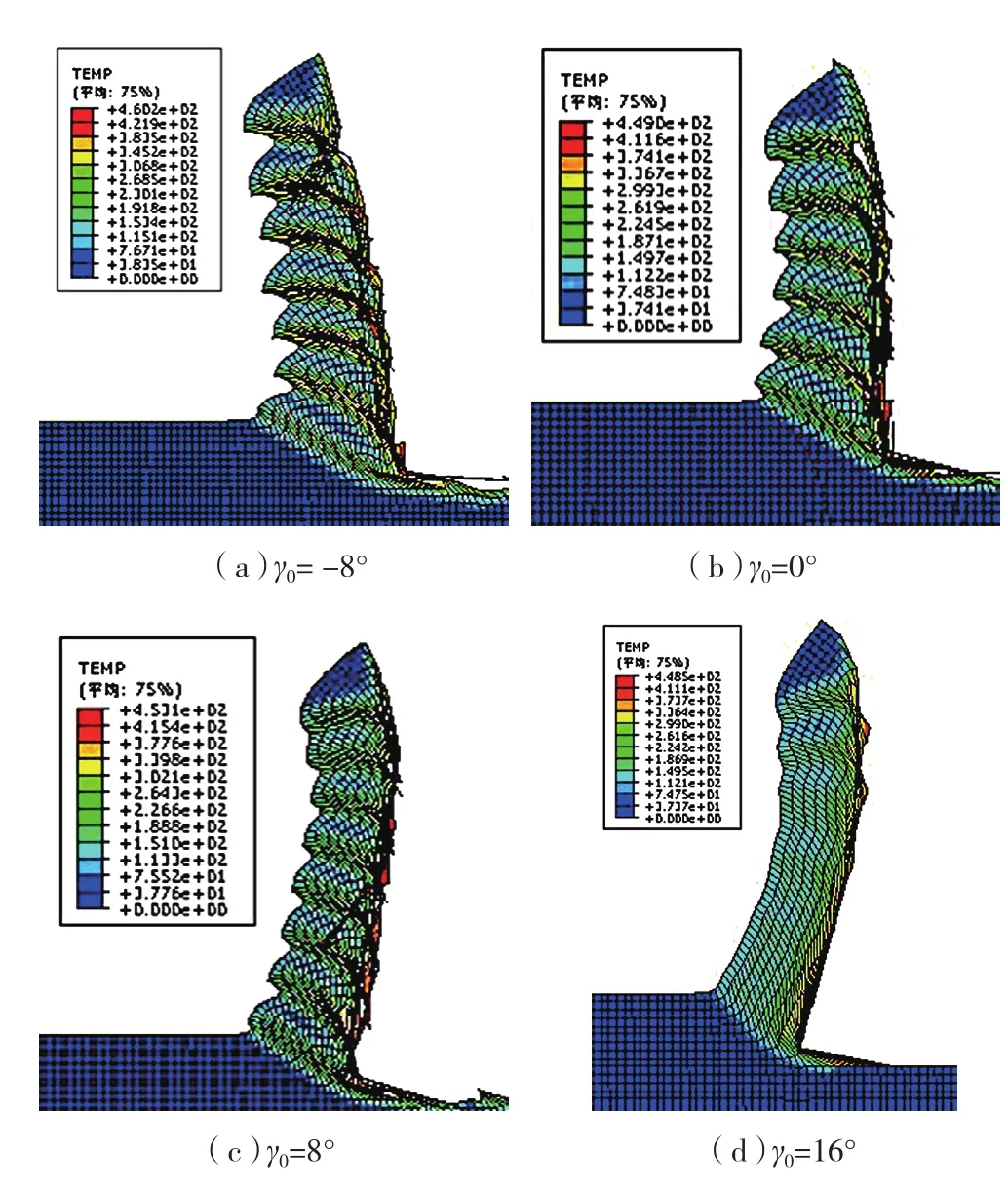
图2 不同前角时的切屑形态Fig.2 Chip morphology of different rake angle

图2为不同前角条件下得到的切屑。γ0为-8°～8°时，形成锯齿状切屑，如图2（a）～（c）所示。因为随着刀具的切入，工件受到挤压和剪切，切削刃前方的金属发生极大的塑性变形，切屑逐渐成形并处于热传导、热对流和热产生速率三者的动态平衡状态。当切削速度增加到某一临界值时就会打破这种平衡状态[10]，导致突变性的局部剪切，进而使切削层网格拉伸严重，形成一个锯齿。随后，刀具继续前进，切屑沿前刀面向上滑移，刚形成的锯齿形切屑单元在向外滑移的过程中，伴随着能量的释放又使刀具与切削层之间重新处于动平衡状态。由于塑性变形使应力和应变急剧增大，平衡状态再次遭到破坏，如此循环往复形成锯齿状切屑[11]。前角为16°时，开始形成连续的带状切屑，已加工表面的粗糙度变小，如图2（d）所示。这是因为7050属于塑性材料，切屑流出时同前刀面接触区的长度较长且摩擦较大，增大刀具前角可以减小摩擦，使切屑前切滑移过程中的滑移量较小，没有达到材料的破坏程度，从而形成带状切屑。带状切屑内表面光滑，使已加工表面质量较好，但容易缠绕工件和刀具，所以选择刀具前角时应考虑切屑形态的影响。

在图2（a）～（d）中沿剪切面方向和水平方向做剪切角φ，则可以看出：随着刀具前角γ0增大，剪切角φ也随之增大，主剪切区内的剪切应变减小，导致切削变形程度减小，即ξ减小，变化规律同式（1）。

3.2 刀具前角对切削温度的影响

从图2还可以看出，切削温度只有一小部分分布在工件内，其余大部分分布在切屑上，说明切削过程中产生的切削热大部分被切屑带走。垂直剪切面方向上的温度梯度很大，离切屑底层越近，温度越高，这是由于底层材料的变形最大，且与前刀面之间有摩擦的缘故。最高温度并没有出现在切屑与刀尖接触的部位，而是在切屑底层离刀尖有一定距离的地方。这是因为切屑沿前刀面流出时，摩擦热不断增加，使得切屑底层的温度来不及冷却便再次达到最大值。

图3 7050不同前角对应的切削温度Fig.3 Cutting temperature under different rake angles of 7050

将图2（a）～（d）中切削温度的平均值进行采集，得到的变化规律同文献[6]中切削温度的变化规律具有较好的一致性，如图3所示。前角为-8°时形成的锯齿状切屑温度最高，为249.3℃，前角增至16°时，形成带状切屑，温度降至233.7℃。这是因为前角增大，切屑受前刀面的挤压和摩擦作用减小，导致单位切削力下降，因而产生的切削热减少，切削温度降低。所以，使用大前角刀具可以降低前刀面的温度。

3.3 刀具前角对切削力的影响

表 3、表 4、表 5、表 6 分别为刀具前角为 -8°、0°、8°、16°时的主切削力Fc和切深抗力Fp。前角为-8°～8°时，切削力随时间的变化是一个“减小-增大-减小-增大”的波动过程。这是因为在锯齿状切屑形成的过程中，刀具的切入使得工件单元受到挤压和剪切而发生塑性变形，随着变形程度加剧，变形抗力增大，切削力增大；当切屑被排出到前刀面时，单元变形达到材料的变形极限，产生失效单元，变形抗力随之下降导致切削力减小。刀具前刀面和切屑的接触节点随着切削的进行一直在变，使得失效单元的数目和位置都不确定，由此便产生了切削力的上下波动。前角为16°时，切削力波动变化小，且稳定在一个数值附近。这是因为形成带状切屑时，工作单元的失效是有规律进行的，即各个时刻失效单元的数目和位置固定，切削过程平稳。

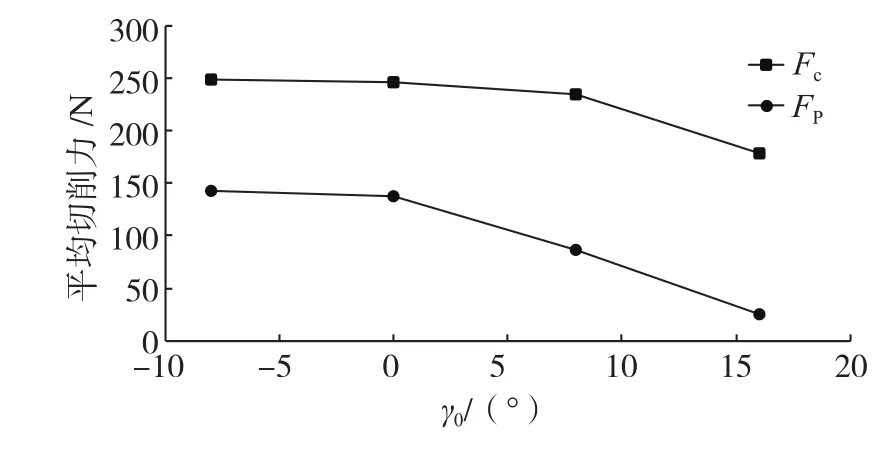
图4 刀具前角对切削力的影响Fig.4 Influence of rake angle on cutting force

图5 试验和模拟切屑形态对比Fig.5 Comparison between experimental and simulated chip morphologies

表3 γ0= -8°时的切削力

表4 γ0=0°时的切削力

表5 γ0=8°时的切削力

表6 γ0=16°时的切削力

将表3、表4、表5、表6中主切削力Fc和切深抗力Fp的平均值进行采集，如图4所示，得到的变化规律同式（3）、式（4）一致。这是因为前角增大，刀具与工件接触的区域变大，切削面积和切削层金属的塑性变形量减小，切屑容易流出，所以切削力降低。随着刀具由负前角向正前角变化，主切削力和切深抗力仍呈下降趋势，但主切削力从0°到16°只下降了68N，而切深抗力的下降梯度很大。故前角对切深抗力的影响比主切削力明显，实际加工中在保证刀具强度的前提下，应尽可能选择大前角刀具。

4 切削试验与仿真结果比较

周军[12]在DAEWOO ACE-V500加工中心上进行了直角切削试验，试件材料为7050，刀具材料为硬质合金，刀具前角为0°，后角为7°，切削速度为 500m/min，切削深度为22μm。对加工后产生的切屑进行镶样、打磨、抛光和腐蚀，在光学显微镜下观测到的切屑微观形貌如图5（a）所示。利用本文建立的有限元模型，在与切削试验相同的条件下模拟预测的切屑形态如图5 （b）所示。通过比较可以看出，切削试验和有限元模拟的切屑形态非常接近，证明了所建模型可以较为准确地预测切削过程中的切屑形态。

5 结论

（1）在一定范围内，切削力和切削温度均随刀具前角的增大而减小。因此，加工7050时，应主要以前角的变化来控制切削力和切削温度，刀具选用大的前角对改善切削过程有利。

（2）刀具前角直接影响切削过程中的切屑形态。前角小于0°时，最容易形成锯齿状切屑，随着前角增大，切屑变形减小，逐渐形成带状切屑。所以，加工7050时，考虑到切屑形态的影响，合理的前角范围为8°～16°。

（3）由于考虑了大应变、高应变率以及温度等因素的影响，切削试验与仿真结果具有较好的一致性，由此可知，本文使用的有限元模型能准确模拟7050的切削过程。

[1]付秀丽, 艾兴, 万熠,等.铝合金7050高温流变应力特征及本构方程[J].武汉理工大学学报, 2006(12):113-116．

FU Xiuli, AI Xing, WAN Yi, et al. Flow stress characteristics and constitutive equation at high temperature for 7050 aluminum alloy[J].Journal of Wuhan University of Technology, 2006(12):113-116．

[2]咸成吉,朴成道,尹凤哲.刀具前后角对切削力和切削温度的影响[J].延边大学学报:自然科学版, 2013, 39(4):289-293.

XIAN Chengji, PIAO Chengdao, YIN Fengzhe. The effect of cutting tool angles on cutting forces and temperatures[J]. Journal of Yanbian University(Natural Science),2013,39(4):289-293.

[3]MUSTAFA G, İHSAN K, ERSAN A, et al. Experimental investigation of the effect of cutting tool rake angle on main cutting force[J].Journal of Materials Processing Technology, 2004, 166(1):44-49.

[4]HACI S, FARUK U, SULEYMAN Y. Investigation of the effect of rake angle and approaching angle on main cutting force and tool tip temperature[J]. International Journal of Machine Tools and Manufacture,2005, 46(2):132-141.

[5]武文革,辛志杰.金属切削原理及刀具[M].北京:国防工业出版社, 2009:45-46,71-72.

WU Wenge, XIN Zhijie. Principles and tools of netal cutting[M].Beijing:National Defense Industry Press, 2009:45-46,71-72.

[6]杨树财.精密切削钛合金Ti6Al4V刀具刃口作用机理及应用研究[D].哈尔滨:哈尔滨理工大学,2011.

YANG Shucai. Action mechanism of cutting tool edge and application in precision machining Ti6Al4V[D]. Harbin:Harbin University of Science and Technology,2011.

[7]孔虎星,郭拉凤,尹晓霞.基于ABAQUS的钛合金切削有限元分析[J].机电技术, 2011, 09:22-23.

KONG Huxing, GUO Lafeng, YIN Xiaoxia. Finite element analysis of titanium cutting based on ABAQUS[J]. Electrical Technology, 2011, 09:22-23.

[8]徐志平.基于有限元方法的切削加工过程动态物理仿真关键技术研究[D].济南:山东大学, 2008.

XU Zhiping. Study on the key technologies of dynamic physical simulation for machining process based on finite element method[D].Jinan:Shandong University, 2008.

[9]冯志喜.基于有限元法的淬硬45钢切削刀具参数研究[D].昆明:昆明理工大学, 2011.

FENG Zhixi. The Research of hardened 45 steel cutting parameters based on finite element method[D]. Kunming: Kunming University of Science and Technology,2011.

[10]王亮德,赵军,郭胜光.锯齿形切屑的计算机仿真[J].机械工程师, 2005, 02:30-32.

WANG Liangde, ZHAO Jun, GUO Shengguan, et al. Computer simulaition for serrated chip formation[J]. Mechanical Engineers,2005,02:30-32.

[11]孟辉.高速切削温度动态有限元建模与数值模拟[D].济南:山东大学, 2005.

MENG Hui. Dynamic finite element modeling and numerical simulation of cutting temperature field in high speed machining[D].Jinan:Shandong University,2005.

[12]周军.铝合金7050-T7451微切加工机理及表面完整性研究[D].济南:山东大学, 2010.

ZHOU Jun. Research on mechanism and surface integrity for micro cutting Al7050-T7451 alloy[D]. Jinan:Shandong University, 2010.