铝7075介观尺度切削过程的仿真研究*

（北京理工大学，北京 100081）

近年来，生产具有军事、医疗用途的微型发动机、血管清道夫以及尺寸微小、功能复杂的微型机电产品正在成为一种趋势，这种产品小型化的趋势使介观制造技术成为研究的热点。介观切削不仅仅是宏观切削在尺寸上的减小，而且存在诸如尺度效应、最小切削厚度等与宏观切削截然不同的特点和机理。由于经典塑性理论不能表现材料在不同尺度层次上的不同力学响应行为，因此不能很好地解释尺度效应。为了解释介观切削中的尺度效应，描述当切削量与材料特征长度相当时的材料变形特征，研究人员引入了基于微观机制的应变梯度（Mechanism-based Strain Gradient，MSG）塑性理论；在MSG理论中，为了平衡应变和应变梯度的量纲引入了材料内禀长度l(长度量纲)，成功揭示了金属材料的尺度效应，即材料强度随特征尺寸的降低而增加的现象。Jin[1]等扩展传统的切削理论，分析了微切削过程中刀具切削刃钝圆半径对尺度效应的影响；Lai[2]、Liu[3]、Ding[4]等将MSG理论运用于材料铜、Al5083、H13模具钢的有限元仿真建模研究之中。

一般微型产品都对产品的轻量化有一定的要求，在铝合金材料中，Al7075具有很高的强度，非常适合用于制造轻量化要求高的飞机承载结构件，如飞机零部件、齿轮和轴等，尤其是微型飞机发动机的零部件[5]。针对Al7075的微切削加工开展基于MSG理论的有限元建模技术研究，首先建立Al7075的介观尺度力学性能的本构关系，然后结合ALE算法建立切削过程有限元仿真模型，最后通过Al7075微切削的有限元仿真，研究介观尺度下Al7075材料的最小切削厚度、单位切削力以及尺度效应。

1 基于应变梯度本构关系的建模

基于MSG的JC修正模型是在基于位错密度的Taylor流变塑性本构方程的基础上推导获得的，如图1所示。公式（1）为基于MSG的JC修正模型表达式：

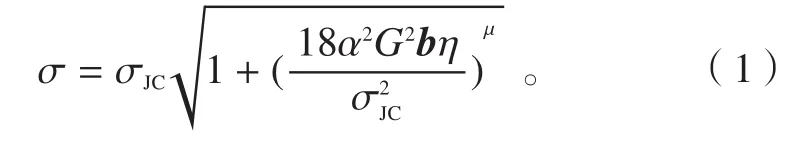
Melkote[6]通过对微切削主变形区位错的分析，获得了主变形区的应变梯度η与切削主剪切变形区长度L之间的关系，其表达式为：

Kim[7]采用分子动力学的方法研究并提出了形成切屑和不形成切屑两种不同介观尺度切削情况的主剪切变形区长度L的计算方法：

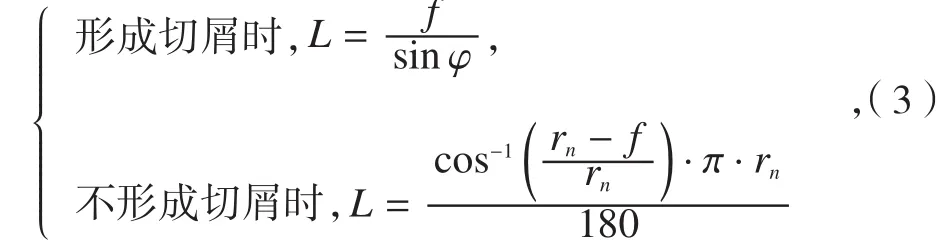
式中：，f为进给量；为剪切角；ae为铣刀周向前角；β为摩擦角；rn为切削刃钝圆半径；对于材料为铝合金，刀具为金刚石刀具来说ζ的常数值为90。

图2为根据式（1）中基于MSG的JC修正模型开发ABAQUS材料本构vumat子程序的流程图。图中：O为状态变量；D为刚度矩阵；σ为应力；ε为应变。

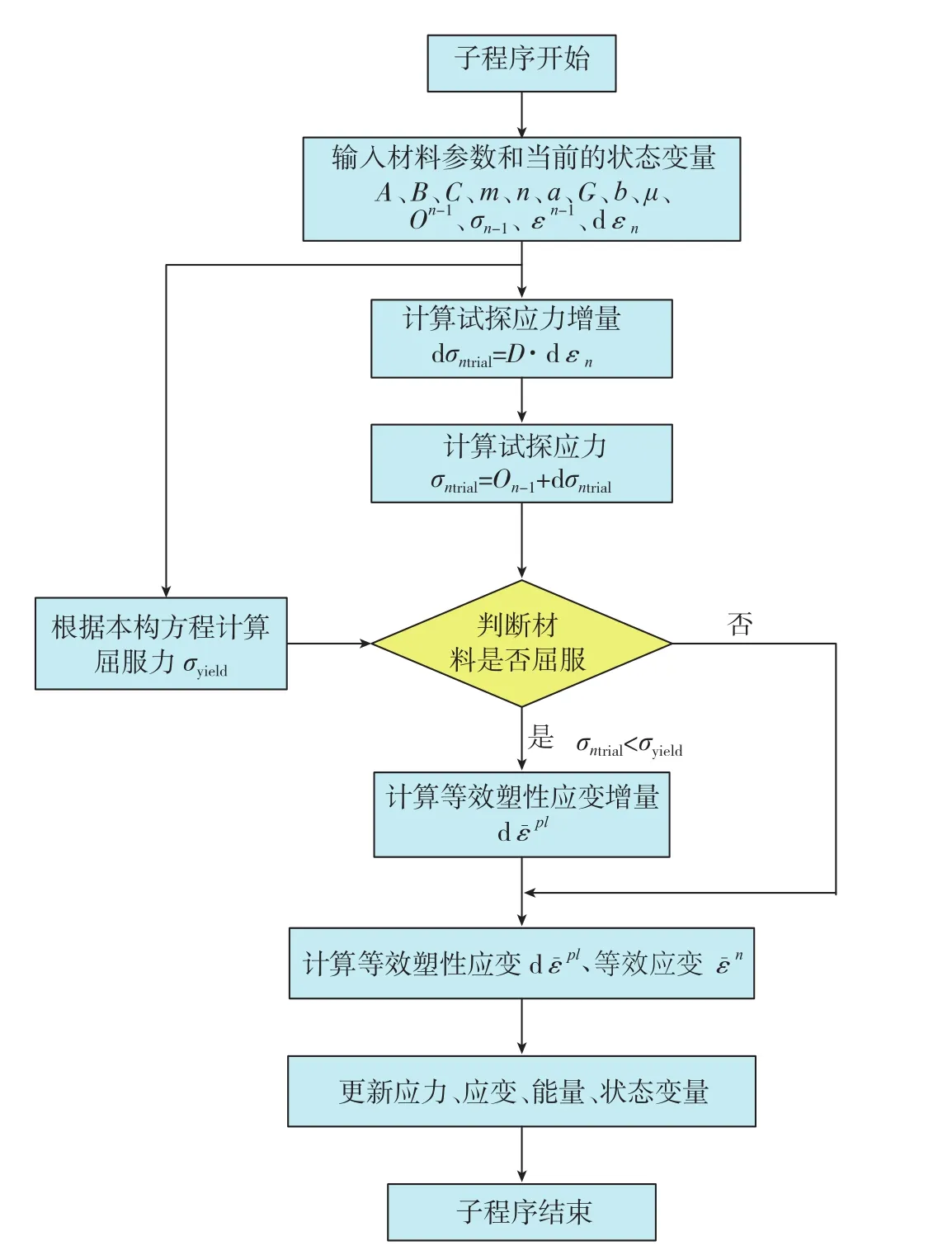
图2 材料本构vumat子程序的流程图Fig.2 Flow chart of the VUMAT program

表1为后续介观切削仿真中所用到的Al7075的材料参数[8-9]，是在经典JC本构模型的材料参数基础上增添了反映材料尺度效应的微观材料参数。

2 基于ALE算法的有限元仿真技术

对于介观尺度切削中切削层的厚度与刀具的刃口钝圆半径同属于一个数量级的情况，不合适的材料分离准则参数设置将会导致切削层内网格单元过多的失效和删除，从而造成仿真预测的切屑厚度远小于实际的切屑厚度，并且预测的其他参数也会产生较大的误差，而材料分离准则参数的正确设置难度较大； ALE算法能够绕开这一问题，无需设置材料失效准则，其切屑的形成是通过工件网格随着刀具不断切入工件而逐渐迁移到刃区前端的切屑分离区以提高这一区域的网格适应性，精确模拟出刃区前端工件材料的变形情况而形成切屑，因此ALE算法非常适合用于介观尺度切削仿真。

图3中工件上表面的网格将会随着刀具不断切入工件而逐渐迁移到刀具刃区的前端，增加表面网格种子的数量有利于增加切削分离区的网格适应性，更加精确地模拟出切削分离的材料变形情况，但是初始网格密度太大将会大幅降低仿真计算的速度。为了既增加网格种子的播撒数量同时又不使初始网格密度过大，将刀具切入工件的部分预先设计出如图3中所示的凹角，从而增加了网格划分时播撒种子的面积。

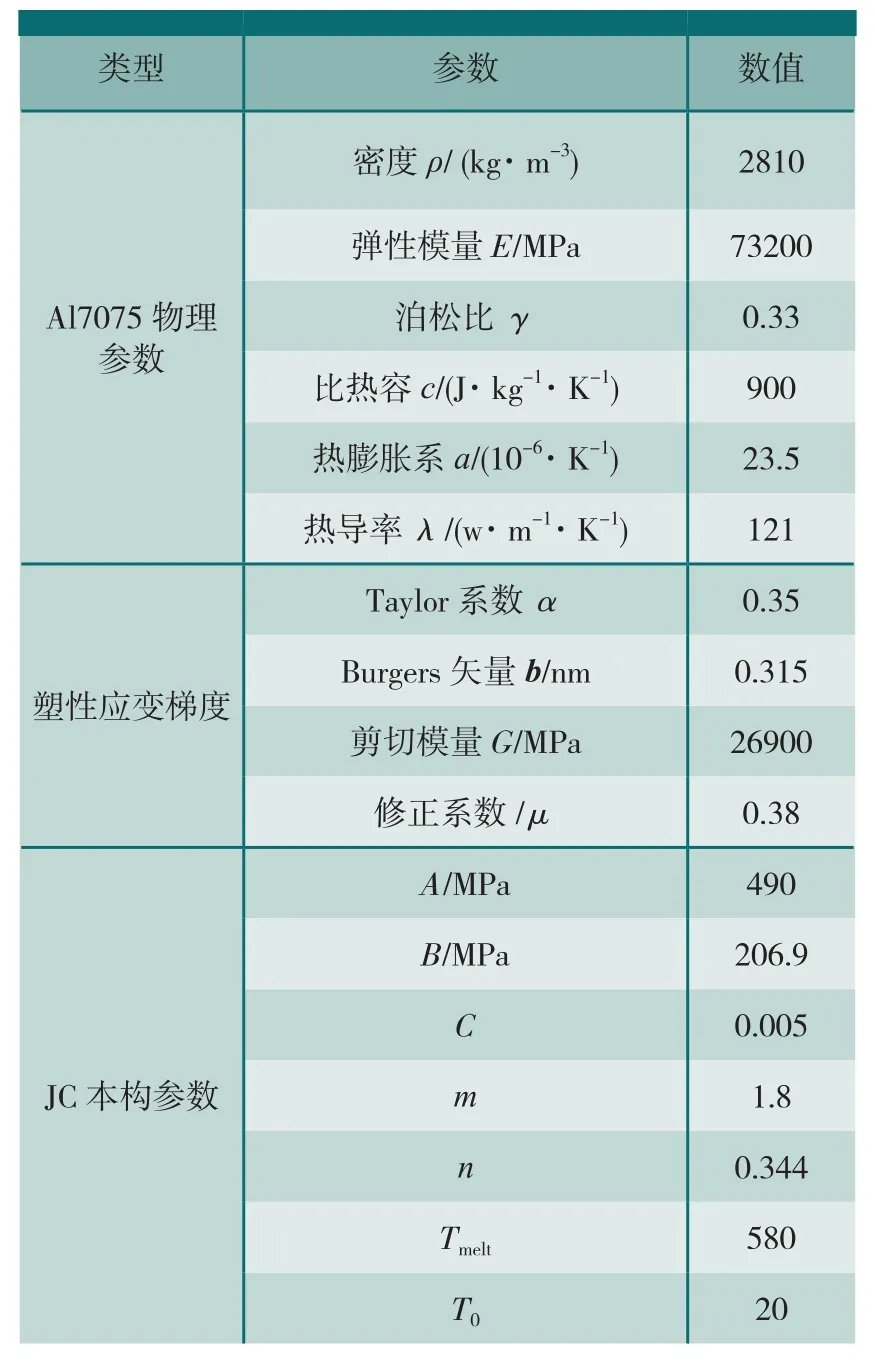
表1 Al7075的材料参数

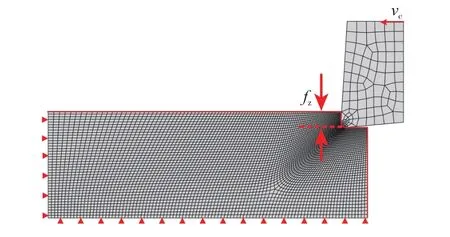
图3 基于ALE算法的切削仿真过程的几何建模和网格划分Fig.3 Geometric modeling and meshing of process of cutting simulation process based on ALE

由于金刚石刀具的硬度远远高于铝合金材料，因此把刀具设定为刚体；整个刀具随着其上选定的一个参考点以切削速度做从右往左的刚体直线运动，逐渐切入工件。在工件的底部和左侧设置约束使其固定不动，工件上表面和右侧表面为拉格朗日边界，其上的网格将会随着材料点移动而形成切屑，同时由于采用了ALE适应性网格重划技术，网格又会进行定期调整以增加切屑分离区的网格适应性。其中，ALE控制参数设置中初始几何特征角度的设置非常重要，一个合适的参数设置能够保证工件上表面的节点不会迁移到工件的左右表面，而又能够在整个上表面上都能流畅地移动[10]。

3 准直角自由铣削试验的设计

试验所用试样材料为Al7075，所用PCD立铣刀的轴向前角为0°，周向前角为3.5°，周向后角为5°，钝圆半径为5μm；安装在Kistler测力仪上的5mm厚平板形的工件中部预先加工出了宽6mm、深4mm的通槽，如图4所示，其目的是为了减小铣削深度至1mm，同时又能尽量保证工件的整体刚度。为实现准直角自由铣削，试验中仅仅使用立铣刀的侧刃铣削掉槽部的材料，即端刃不参与切削，因此铣削深度等于槽部工件材料的厚度，即1mm；铣削试验设备为DMG monoblock DMU80镗铣加工中心（X和Y方向的定位精度为8μm）；铣削力的测量仪器为Kistler9257B型测力仪，量程采用50N，其灵敏度为-7.92pC/N，线性度为0.1%F.S.。

为了研究介观尺度铣削的尺度效应中进给量与刃口半径之比对切削力等介观尺度切削过程变量的影响规律，本文进行了如表2所示的多组变进给单因素试验。

图4 工件和刀具相对位置及安装Fig.4 Installation and the relative position of the workpiece and machine tool

表2 试验参数

4 试验与仿真结果分析

4.1 两种仿真模型的对比与试验验证

从图5中可以看出，铣削力随着每齿进给量的增加而不断增大，并且Fy大于Fx；另外，基于MSG的JC修正模型仿真得到的切削力更接近试验值，而用经典JC模型预测的切削力则比实验值小很多。通过切削力的对比可以证明在微观切削中由于几何必需位错的存在对材料造成了硬化作用，使材料产生了尺度效应，导致使用经典JC本构模型计算得出的塑性屈服应力以及材料流动应力值比真实材料屈服应力小了许多，所以仿真得到的切削力明显小于试验测量值。

图6中的3条曲线都表明：单位切削力随着进给量的减小而增加，材料呈现出了“越小越强”的尺度效应；其中基于MSG的JC修正仿真模型比经典JC仿真模型预测的单位切削力更接近试验值，而且经典JC模型预测的误差会随着进给量减小不断增加。采用经典JC模型预测的单位切削力也会随着进给量减小而增加，其原因在于：进给量减小，刀屑接触区域下移导致刀具工作前角为负值；进给量越小，负值越大，切削变形系数增加，因此单位切削力增加。

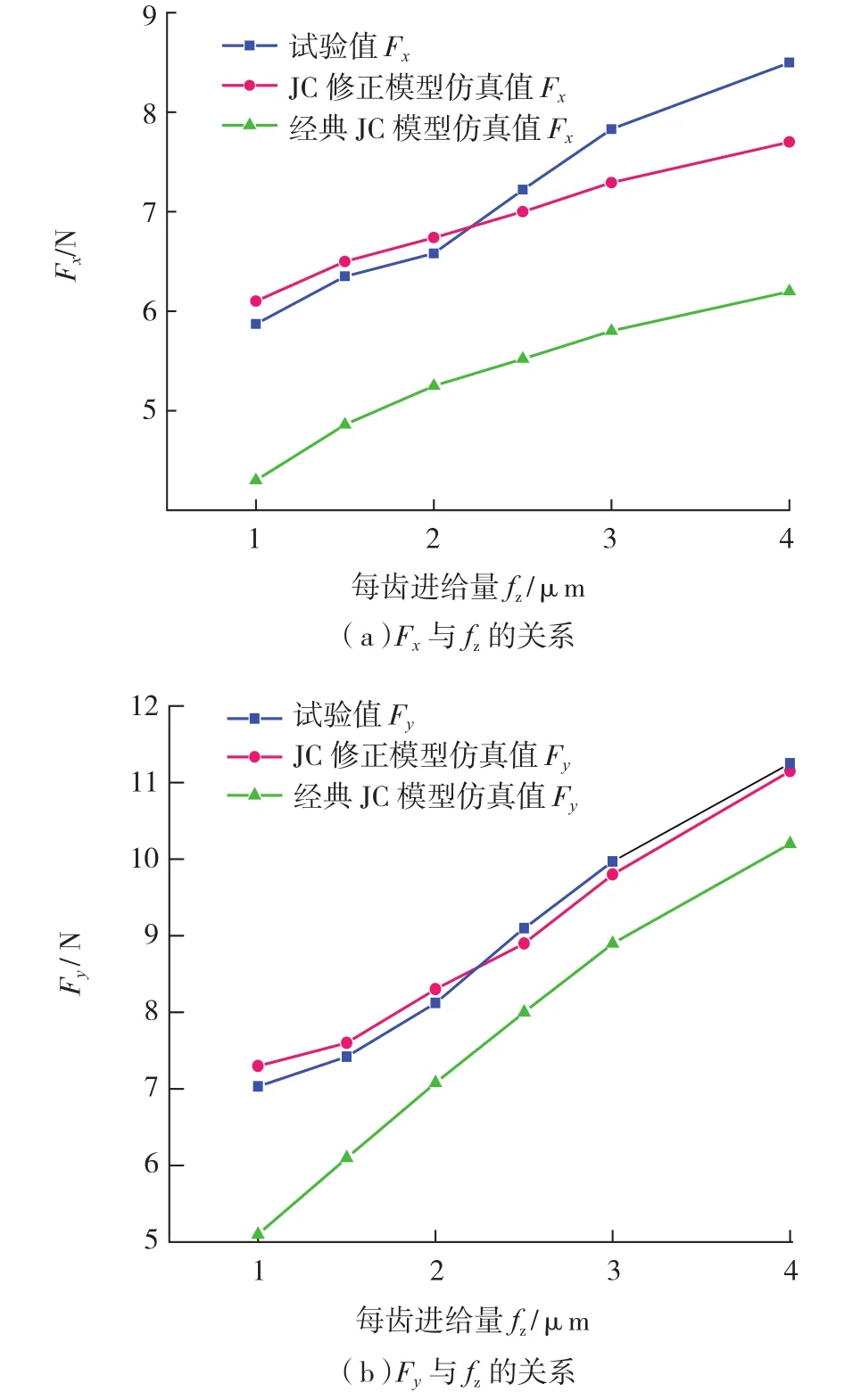
图5 实验和仿真铣削力对比Fig.5 Comparisons of milling forces between the experimental and predicted results

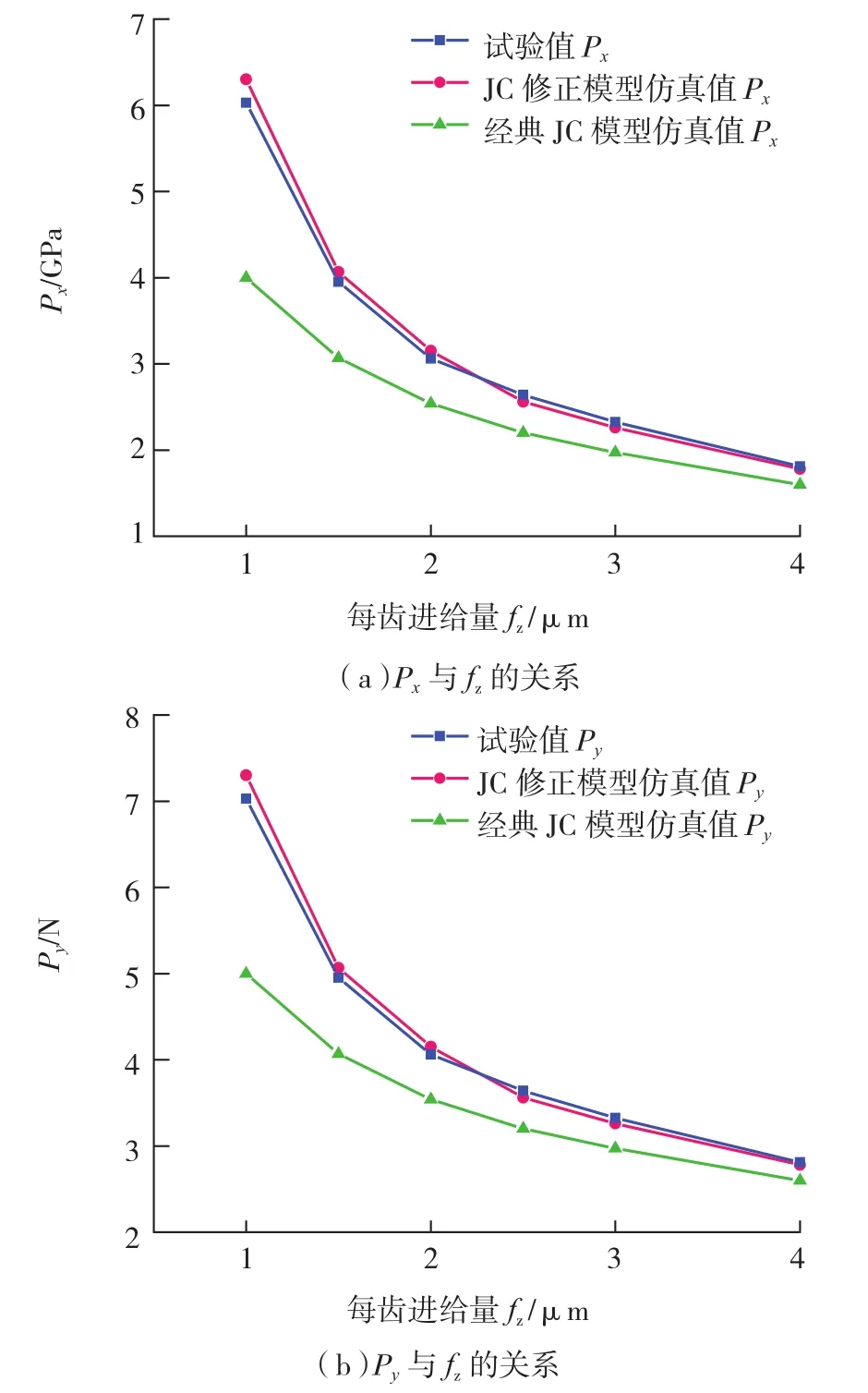
图6 单位切削力随进给量的变化规律Fig.6 Unit cutting force at different feed per tooth

4.2 最小切削厚度的分析

最小切削厚度是指由切削到完全耕犁转变的一个临界值，是介观切削中非常重要的一个参数。它与刀具刃口的钝圆半径R有关。图7针对切削厚度（对应于铣削的每齿进给量）为 0.2R(1μm)、0.25R(1.25μm)、0.3R(1.5μm)3种情况进行了二维切削仿真。从图中可以明显地看出，当切削厚度为0.2R时不能产生切屑，0.25R时是即将形成切屑的临界情况，但材料在前刀面发生了累计效应，0.3R时产生了明显的切屑。因此，刃口钝圆半径为5μm的PCD刀具切削AL7075时，最小切削厚度应该在 0.25R(1.25μm)～0.3R(1.5μm)之间。

4.3 尺度效应对等效应力的影响

以每齿进给量为2.8μm时为例，研究相同切削条件下基于MSG的JC修正模型与经典JC模型两种材料本构模型对切削区的等效应力分布的影响。通过图8中（a）和（c）、（b）和（d）应力分布图的比较可以发现，两种仿真模型预测的切削区的应力分布的相似之处在于：最大应力的区域位于紧密围绕着刀具刃口半径的切削层部分；但是基于MSG的JC修正模型预测的最大应力值比经典JC模型预测的最大应力值要高出很多。在介观尺度切削中除了存在宏观尺度切削中的统计存储位错，还存在着尺度效应引起的几何必须位错，由此造成的位错密度增值必定导致介观尺度相应切削区域中应力值的增加，基于MSG的JC修正模型很好地反映了这种现象。

采用基于MSG的JC修正模型针对进给量分别为2μm、8μm的切削过程进行了分析，以研究随着切削厚度的变化，尺度效应对等效应力分布的影响。由图8中（a）和（b）可见，随着进给量的减小，切削区的最大应力值在增加，分别为 1177MPa、1028MPa，而由图 8中（c）和（d）可知，经典JC模型预测的切削区最大应力保持稳定，数值变化不大，说明随着进给量减小而最大应力值增加基本是由几何必需位错密度增值产生的。

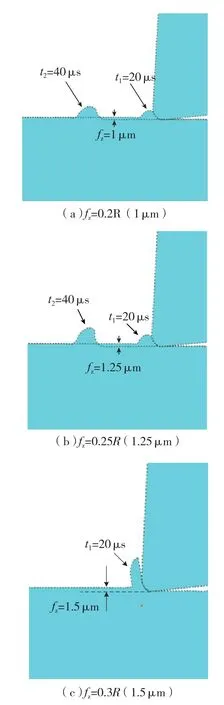
图7 根据仿真结果确定形成切屑的最小进给量Fig.7 Minimum chip thickness based on the simulation results of chip formation

图8 仿真模型对切削区应力分布情况的预测对比Fig.8 Comparison of the stress distribution based on the simulation results

5 结论

（1）基于MSG的JC修正模型能够正确反映切削厚度减小引起的几何必需位错密度的增值现象，即尺度效应，比经典的JC模型更适合于介观尺度切削的仿真，所预测的切削力和单位切削力更接近试验值。

（2）采用基于MSG的JC修正模型得到了PCD刀具切削铝合金Al7075的最小切削厚度，其值大概为刀具钝圆半径的0.25～0.3倍。

（3）基于MSG的JC修正模型的仿真研究表明：随着切削厚度的减小，切削区的最大应力值大幅增加，这种最大应力值的增加基本是由几何必需位错密度增值产生的。

[1]JIN X L, ALTINTAS Y. Slip-line field model of micro-cutting processwith round tool edge effect[J]. Journal of Materials Processing Technology (S0924-0136), 2011, 221(3): 335-359.

[2]LAI X M, LI H T, LI C F, et al. Modeling and analysis of micro scalemilling considering size effect, micro cutter edge radius andminimum chip thickness[J]. International Journal of Machine Toolsand Manufacture(S0890-6955), 2008, 48(1): 1-14.

[3]LIU K. Process modeling of micro-cutting including strain gradient effects[D]. Gerorgion: Georgia Institute of Technology, 2005.

[4]DING H T, SHEN N G, SHIN Y C. Experimental evaluation andmodeling analysis of micro-milling of hardened H13 tool steels. Journal of Manufacturing Science and Engineering (S1087-1357), 2011, 133(4):1-11.

[5]赵丽丽，张以都，邬 亮. 7075薄壁件二维单刃切削的有限元仿真 [J]. 航空制造技术，2005(8)：74-77.ZHAO Lili, ZHANG Yidu, WU Liang. Finite element simulation of 2D single blade cutting for 7075 thin-wallworkpice[J]. Aeronautical Manufacturing Technology,2007(8):74-77.

[6]JOSHI S S, MELKOTE S N. An explanation for the size effect inmachining using strain gradient plasticity[J]. ASME Journal of Manufacturing Science and Engineering, 2004(126): 679-684.

[7]KIM C J. Mechanism of the chip formation and cutting dynamic of the micro scale milling process[D]. Dissertation of the University of Michigan, 2004.

[8]周军. 铝合金7075-T745微切削加工机理及表面完整性研究[D]. 山东：山东大学，2010.ZHOU Jun. Reseach on mechanism and surface integrity for micro cutting AL 7050-T745 alloy[D]. Shandong : Shandong University, 2010.

[9]SUBBIAH S. Effect of finite edge radius on ductile fracture ahead ofthe cutting tool edge in micro-cutting of Al2024-T3[J]. Materials Science and Engineering: A (S0921-5093), 2008, 474(1): 283-300.

[10]XIE L J. Estimation of two-dimension tool wear based on finite element method[D]. Germeny: University of karlsruhe (TH), 2004.