外翼上壁板根部连接形式对飞机承载能力的影响研究

赵 翔 ，张妮娜 ，张俊龙

（1.西北工业大学工程力学系,西安 710129；2.中国航天科工集团第六研究院四十一所，呼和浩特 010010；3.中航飞机股份有限公司西安飞机分公司，西安 710089）

在飞机的结构设计中，搭接接头常用来连接和组装飞机的各重要受力结构，实现各部件之间的载荷传递和分配，飞机结构的破坏多源于这种连接细节[1]。飞机机翼壁板根部连接处的结构形式对飞机的传力和承载能力具有重要的影响，而且这些连接通常采用多钉的连接方式，正确分析接头的整体受力特性以及钉孔孔边应力分布特征是减小其应力集中的基础与关键[2-3]。

虽然可以通过试验的方法得到结构在外载下的受力分布，但是由于测量应变的数量有限，并且载荷的传递效率随结构形式的变化规律需要通过大量试验进行测试，需要耗费大量的人力物力和时间。随着型号研制任务的日益繁重，完全通过试验来探索结构的最优传力形式是不现实的[4-5]。有限元方法作为一种数值计算手段，结合试验验证的方法，在目前的研发性试验中具有广泛的应用，例如高扬等[6]使用有限元法对某机翼连接接头的应力进行了分析，并对界面的构型进行了优化设计，可有效减少飞机的设计周期。陈磊等[7]采用有限元方法对飞机结构设计中的传力路径进行了量化，得到了最佳的传力路径，对传统的优化方法具有较大的指导作用。邱春图等[8]研究了有限元模型符合试验结果的条件，提出对有限元模型根据试验数据进行调整，才能得到可靠的有限元模型。

关于多钉连接结构的分析，目前有解析法、试验研究以及有限元计算分析法。由于紧固件与孔边的变形和应力状态相当复杂，难以用数学表达式进行描述，且各钉之间相互影响导致旁路载荷与钉载的测定非常困难，有限元方法成为该领域应用最为广泛的研究手段。陈海欢等[9]用4种简化螺钉单元计算分析了单搭接多排连接结构的钉载分配，并对其进行了对比研究，发现组合单元可更准确地计算紧固件的钉载。刘向东等[10]通过应变电测技术获得连接件典型截面应变分布，再间接估算钉载分配比例，建立了试验件二维、三维有限元模型，发现虽然应变的计算与实测值吻合，但是钉载的分配计算结果与实测结果存在较大偏差。

本文通过对某飞机机翼上壁板不同形式的根部连接进行压缩试验，并加载至破坏，以评定各类型的承载能力及传力效率。通过有限元方法，建立考虑螺钉的三维有限元模型，对连接形式进行优化并分析破坏的原因，研究各螺钉的钉载分配，优选出适合某飞机的根部连接形式，为机翼壁板根部连接结构的优化设计提供依据。

1 外翼上壁板的压缩对比试验

上壁板根部的连接形式为3种方案：A类1型、A类2型和B类。通过静力压缩试验研究壁板根部连接处的传力、变形、承载能力，将载荷加载至破坏，对破坏结果的原因进行分析，对3种类型进行对比分析，形成优选结果。

应变片分布如图1～2所示，根据有限元理论计算得到上壁板的估计极限载荷值，然后根据该极限载荷值制定初步试验加载方案。试验过程中，首先按照极限载荷值的5%进行预加载，逐级加至15%（每级5%），保持30s，卸载至零载荷，检查试验件、夹具和仪器，最终确定后面所有试验件的最后加载方案，根据理论计算上壁板的极限载荷值为650kN。

图1 A类1型、A类2型侧面和正面根部连接形式应变片分布Fig.1 Frontal and profile view images the strain qaqes distribution of the strain gages distribution of type A-1 and A-2

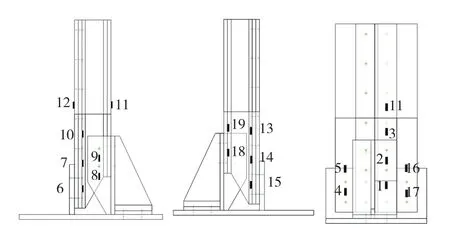
图2 B类的侧面和正面根部连接形式应变片分布Fig.2 Frontal and profile view images of the strain gages distribution of type B

2 试验结果

由于试件的长宽之比较小，因此可以忽略附加弯矩的影响。3种类型的载荷-位移曲线如图3所示。从图3中可以得到各型试验件平均破坏载荷数据：压缩A类1型平均破坏载荷为600.75kN；压缩A类2型平均破坏载荷为640.35kN；压缩B类平均破坏载荷为563.86kN。

A类1型在初始压缩加载阶段（1～3mm）载荷较高，但是最后破坏载荷最高的是A类2型，其破坏载荷为640.35kN。由于结构主要在弹性范围内工作，因此单凭破坏载荷，并不能代表其承载能力就高，还需要研究结构的应力集中、螺钉载荷甚至是屈服载荷来衡量方案的优劣。

从测试结果来看，结构的应力集中均发生在长桁与壁板根部的连接位置，也就是3号、10号应变片的位置，破坏载荷时应力水平可达到370MPa。压缩试验中，试验件失效都是由于螺栓受剪断裂导致，根据应变测试结果可以得到A类1型铆钉之间的载荷分配更均匀。相比A类1型试件，虽然A类2型试件的破坏载荷较高，但是在同一载荷水平下，其变形更大。在飞机结构中，考虑强度因素的同时，还需要考虑结构刚度的因素。因此，A类1型试件的结构更趋合理。

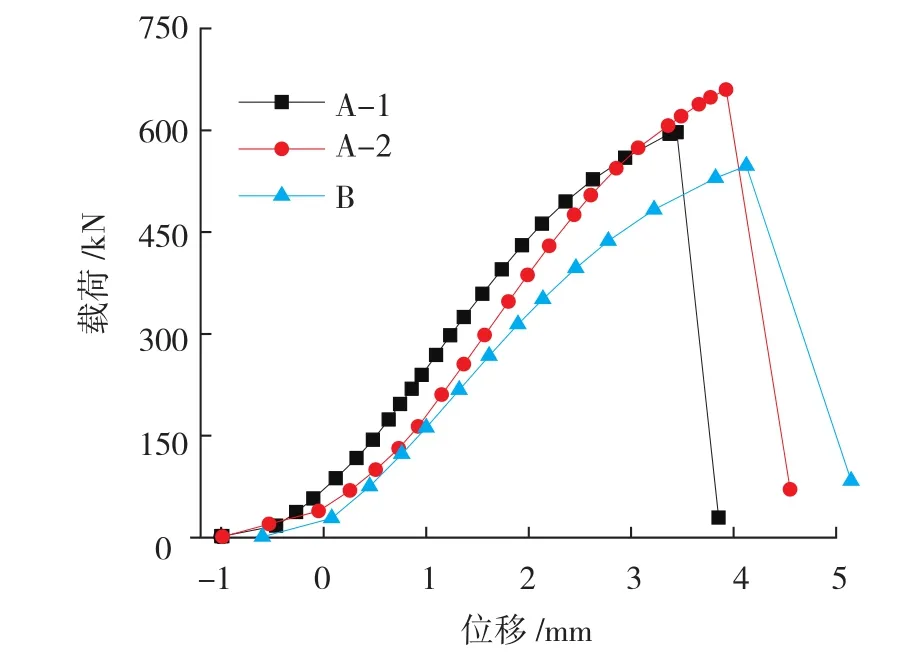
图3 上壁板压缩试验载荷-位移曲线Fig.3 Load-displacement curve of the outboard wing panels in compressive tests

3 外翼上壁板的有限元模拟

3.1 模型参数

采用Abaqus有限元软件进行模拟，上壁板3种选型方案CAE模型，固支底面，上面通过耦合方法施加向下的位移边界条件（压缩），如图4所示，最大位移为6mm。长桁根部与连接处采用螺栓连接，蒙皮和长桁螺栓半径为4mm，螺栓的剪切力为41.386kN；其余螺栓半径为4.5mm，其剪切力为64.944kN；结构各个零部件的材料性能如表1所示。

图4 上壁板压缩有限元模型示意Fig.4 FEM of the top panel

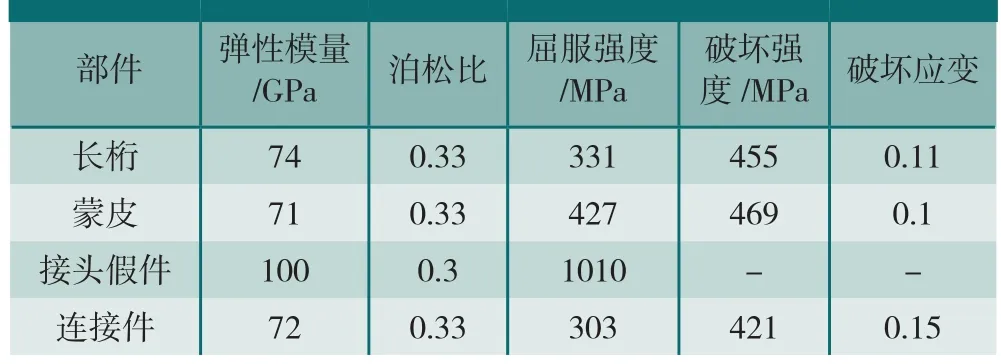
表1 各部件的力学性能

3.2 计算结果

计算得到3种方案结构的载荷-位移曲线如图5所示，在最开始加载阶段（1～3mm）时，A类1型方案的载荷较高；当超过3mm时，A类2型方案的载荷超过1号方案成为最高，B类方案始终载荷较小。根据载荷-位移曲线可以预估结构的破坏载荷，A类1型方案破坏载荷约在600kN左右，A类2型方案破坏载荷约在700kN左右，B类方案破坏载荷约在600kN左右。由于在结构中不能允许材料发生塑性变形，所以只看破坏载荷的大小是不够的，需要衡量它们屈服载荷的大小，如表2所示。在上壁板A类1型方案的MISES应力云如图6所示，可以看出，螺栓对上壁板结构的承载有较大的影响。

由于上壁板破坏方式为螺栓剪断，因此提取压缩载荷对应的螺栓载荷如果达到螺栓的剪切载荷，则说明试件破坏断裂。螺钉编号A类2型方案的压缩载荷达到600kN 左右时，6、7、10、11号螺钉其剪切载荷达到破坏值64.944kN，说明这4个螺栓的承载比较大。A类1型与B类、A类2型方案类似，都是6、7、10、11号螺钉首先达到破坏载荷，当达到屈服载荷时各方案的螺钉载荷数据如表3所示，计算得到的螺钉载荷之和约等于施加的屈服载荷。

针对3种方案，比较每种方案各个螺栓之间最小剪切力与最大剪切力之比（设计时尽可能满足最小值与最大值的比接近1，以使各个螺栓之间的剪切力分布更均匀）。3种方案各自螺栓所受剪力的最小值与最大值之比分别为0.831（26.399kN/31.789kN）、0.826（23.442kN/28.387kN）、0.707（20.415kN/28.878kN），从比值的大小可以说明为什么上壁板A类1型方案的承载能力最好。

图5 有限元计算得到结构的载荷-位移曲线Fig.5 Load-displacement curve of the top panel calculated by FE

3.3 长桁根部形状的影响

表2 有限元计算得到各方案的屈服载荷大小

表3 3种方案的螺钉载荷

通过计算和试验均得到A类1型方案的承载能力较强，由于本试验目的主要是考察根部搭接的形式对结果的影响。A类1型的原始方案中的斜角角度为30°，这里考察斜角为20°、25°、35°时（相应的，接头长度、螺钉位置都会有变化），A类1型方案结构的屈服载荷和应力分布。

对于A类1型方案，考虑长桁根部斜角的变化，原始斜角为30°，这里考察斜角为20°、25°、35°时（相应的接头长度、螺钉位置都会有变化），结构的屈服载荷和应力分布通过计算得到，20°斜角结构的屈服载荷为236kN，相应的位移为1mm；斜角为25°、30°、35°时结构的屈服载荷分别为294kN、354kN、306kN，屈服载荷随斜角角度变化如图7所示，说明试验中选择的30°斜角是最好的。

图6 A类1型达到屈服载荷时的等效应力云Fig.6 Cloud of equivalent stress of A-1 while the panel is led to the yielded state

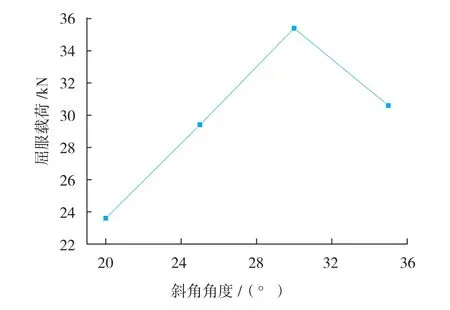
图7 屈服载荷随斜角角度的变化Fig.7 Yield load changes with angle

4 结论

本文通过试验测试和有限元计算的方法，对某飞机机翼根部典型长桁与蒙皮壁板根部连接的承载能力、钉载、失效模式进行了分析。通过试验发现，上壁板A类1型方案的综合承载能力最好，其主要破坏方式为螺栓的剪切断裂。根据有限元计算结果发现，A类1型方案的屈服载荷为354kN，在3种方案中最高，并且各螺栓的受力更为均匀。通过对长桁根部不同斜角的计算发现，当斜角为30°时，A类1型方案的屈服载荷最高。

[1]杨海波,孙秦.某机翼复杂接头的经济性和耐久性设计研究[J].航空计算技术, 2006,36(6):73-75.

YANG Haibo, SUN Qin.Design on economization and endurance of complex joint on x-plane wing[J].Aeronautical Computing Technique,2006, 36(6):73-75.

[2]徐建新，陈文俊，李顶河.有限厚板中并排钉载孔边应力集中分析[J].机械强度, 2013(3):386-390.

XU Jianxin, CHEN Wenjun, LI Dinghe.Analysis of stress concentration around two pin-loaded holes arranged in parallel in finite thickness plate[J].Journal of Mechanical Strength, 2013(3):386-390.

[3]马振云, 何景武, 梁猛.机翼/主起落架连接结构传力路线分析[J].长沙航空职业技术学院学报, 2010,10(4):28-31.

MA Zhenyun, HE Jingwu, LIANG Meng.Analysis of load transmission line on the joint structure between the wing and landing gear[J].Journal of Changsha Aeronautical Vocational and Technical College, 2010,10(4):28-31.

[4]王远达, 梁永胜, 王宏伟.飞机结构的耐久性与损伤容限设计[J].飞机设计, 2009, 29(1):37-43.

WANG Yuanda, LIANG Yongsheng, WANG Hongwei.Design of durability and damage tolerance for aircraft structure[J].Aerocraft Design,2009, 29(1):37-43.

[5]刘勇俊, 岳珠峰, 邵小军,等.含多个穿透裂纹的多孔紧固件传载结构裂尖应力强度因子研究[J].机械强度, 2009, 31(6):986-991.

LIU Yongjun, YUE Zhufeng, SHAO Xiaojun, et al.Stress intensity factors for multi-fastener-hole structures with multi-through-cracks[J].Journal of Mechanical Strength, 2009, 31(6):986-991.

[6]高扬，孙秦.多排钉金属连接接头有限元分析方法研究[J].航空工程进展, 2012,3(1):60-63.

GAO Yang, SUN Qin.Research on finite element analysis of multirivet lap metallic joints[J].Advances in Aeronautical Acience and Engineering, 2012,3(1):60-63.

[7]陈磊， 金海波.基于传力路径的飞机加强框结构优化方法研究[J].航空工程进展, 2011, 2(2):199-204.

CHEN Lei, JIN Haibo.Research on structural optimization method for aircraft bulkhead based on the path of force transfer[J].Advances in Aeronautical Acience and Engineering, 2011, 2(2):199-204.

[8]邱春图，成万植.借助静力试验实测值修正和确认全机有限元模型[J], 飞机设计, 2004(2):37-41.

QIU Chuntu, CHENG Wanzhi.Corrected and validated finite element model of an aircraft according to static testing data[J].Aerocraft Design,2004(2):37-41.

[9]陈海欢, 刘汉旭, 李泽江.飞机结构多钉连接有限元计算分析[J].航空工程进展, 2012, 3(4): 457-462.

CHEN Haihuan, LIU Hanxu, LI Zejiang.Finite element analysis of multi-fastened aircraft structural joints[J].Advances in Aeronautical Acience and Engineering, 2012, 3(4): 457-462.

[10]刘向东, 李亚智, 舒怀, 等.多钉连接钉载分配特性研究方法[J].复合材料学报, 2013, 30(1): 210-217.

LIU Xiangdong, LI Yazhi, SHU Huai, et al, Experimental and numerical study on the pin-load distribution of multiple-bolted joints[J].Acta Materiae Compositae Sinica, 2013, 30(1): 210-217.