A computational analysis of the impact of mass transport and shear on three-dimensional stem cell cultures in perfused micro-bioreactors

Himanshu Kaul ,Yiannis Ventikos ,Zhanfeng Cui

1 Institute of Biomedical Engineering,Department of Engineering Science,University of Oxford,Old Road Campus Research Building,Headington,Oxford OX3 7DQ,UK

2 Department of Computer Science,University of Shef field,Regent Court,Shef field S1 4DP,UK

3 Department of Mechanical Engineering,University College London,Torrington Place,London WC1E 7JE,UK

1.Introduction

The principles of tissue engineering can be employed to develop,ex vivo,clinically viable,autologous substitutes with remarkably similar properties and functionality as those of the host tissues in order to replace or regenerate human cells,tissues,or organs[1-5].This,however,requires recapitulation of certain key developmental events ex vivo thereby necessitating tight control over the artificial grow th environment,as w ell as robust and cost-effective manufacturing processes compliant with the evolving regulatory framework[6,7].Bioreactors,based on the premise that certain aspects of the dynamic three-dimensional(3D)environment influence the development of native tissues,are devices that have been successfully utilised towards this end[6,8,9],especially considering the fact that their use makes the entire procedure of cell expansion and development of biologically functional synthetic substitutes less-labour intensive,automated and tractable[6,10].

Despite the technological advances made in the sector of cell therapy and bioreactor technology,bioreactors remain mostly functional‘black boxes’w here trial and error eventually leads to the desired outcome.Assuch,typical bioreactor yields(in terms of desired cellular phenotypes or microbial contamination)are qualitatively poor and theprocessof cell expansion almost non-reproducible[11].This stems from the fact that the impact of factors such as transport phenomena, fluid flow,and shear stresses on the expansion,differentiation and grow th of cells within a bioreactor,both qualitatively and quantitatively,is poorly understood.Computational Fluid Dynamics(CFD)is a mathematical tool that investigators have recently started utilising to analyse the effect of fluidic forces and stresses on cells[12-16].The numerical solution of relevant conservation equations results in the evaluation of field quantities of interest,such ashydrodynamic,mechanical,concentration pro files etc.;usually defined within a desirable physical con figuration of arbitrary shape.In most cases,these equations do not lend themselves to analytical solution;thus numerical techniques become the only non-experimental w ay to acquire insight on relevant dynamics.While numerical solutions are of course approximations to the real physical system processes,CFDcan be employed to characterise the dynamic environment of the native tissue or other synthetic environments,as Song et al.[17]reported,with high fidelity.Such techniques can therefore be used to optimise bioreactor design or flow conditions with the aim to obtain desirable cell grow th,differentiation,or expansion,as they enable full characterisation of 3D flow fields,concentration gradients,and loads in arbitrary geometries.

The application of CFD to characterise local fluid dynamics in a variety of bioreactor systems(concentric cylinder,direct-perfusion,rotating hollow- fibre,rotating-w all perfused,wavy-walled)can already be found in the literature[13,18-22].Song et al.[17]used CFD to predict 3D flow fields at the length scale of stem cells.They employed the Microscale Particle Image Velocimetry technique to experimentally measure flow values,and thereby validate the CFD model.Their investigation concluded that CFD predicts flow regimes within 12%of experimentally measured values in the absence of cells(i.e.12%difference between computationally predicted and experimentally measured shear rate values).CFD was also used to model perfusion and the influence of perfusion generated shear stress on 3D cultures[23].Boschetti et al.[24]investigated shear stress generation as a function of parameters,such as scaffold porosity and pore size,medium flow rate,and diameter of the perfused scaffold section.A 3D CFD model[22]was created to investigate mass transfer interactions between the culture medium and micro-carrier attached aggregated hepatocytes seeded within a hollow-fibre bioreactor.In particular,distribution of oxygen within the cellular compartment and cellular consumption of oxygen as an index of cell metabolic activity were analysed.The overall performance of the numerical model in predicting optimal conditions for culturing viable microcarrier-attached aggregated hepatocytes,despite certain limitations that were a by-product of unavoidable simpli fications,was reported to be satisfactory.

Yu et al.[25]created a numerical model to simulate fluid- flow and oxygen transport in a rotating magnetic bar mixer micro-bioreactor,aiming to determine the operating parameters for animal cell culture.A comparative analysis between a bi-axial bioreactor vessel and its uni-axial counterpart using CFD simulations revealed significant increase in velocity w hen the bi-axial con figuration was used,thereby recommending bi-axial rotation of the vessel as a solution to the problem of inadequate fluid and metabolite transport to and from the cells[26].CFDsmulations were also used to test the hypo thesis that geometrical design of micro-pillars in a micro fluidic channel will affect fluid flow pro files and,therefore,cell immobilisation efficiency of the micropillar array[27].According to the CFD analysis,parallelogram shaped micropillars were found to be superior compared with their semi-circular counterparts as the former delivered more optimal flow pro files that minimised the risk of clogging.The results were verified experimentally.

In this study,a multi-physics CFD platform was employed to analyse and compare the impact of bioreactor variables(such as its geometry,medium flow-rate,choice of scaffold encapsulating cells,number of cells encapsulated in the scaffold)on mass transport and fluid flow in the bioreactor and,therefore,on the expansion and grow th of metabolising mesenchymal stem cells,encapsulated in a slab-shaped scaffold and in a spherical alginate bead under perfused conditions.This entailed modelling,in silico,of the perfusion of cells in a microbioreactor platform,similar to Tissue Flex®(Zyoxel Ltd,Oxford,UK),which was developed to conduct cell and tissue culture under almost uniform(in terms of distribution of metabolite/non-metabolite concentrations and shear,as w e demonstrate in our results)and precisely controlled environment in a midthroughput and parallel manner[10].Model variables included bioreactor con figuration,scaffold morphology,media inlet velocity,glucose concentration in culture media,mesenchymal stem cell metabolism(in terms of glucose consumption),cell density,and apoptotic threshold.Human mesenchymal stem cells(h MSCs)were particularly modelled due to their ease of culture,sourcing from patients,plasticity,and potential for autologous therapy.The importance of 3D cell cultures in providing the growing cellular population with a pseudo-native environment has become clearer over the last few years and was,therefore,included in this study.The model provides insight into glucose transport occurring within the bioreactor.The different variables are listed in Table 1 and the two bioreactor con figurations tested are show n in Fig.1.

Table 1 Variables utilised in the model

2.Material and Methods

2.1.Bioreactor dimensions and con figuration

In order to design the geometry of the model bioreactor,dimensions of Tissue Flex®(Zyoxel Limited,Oxford,UK)microbioreactor were considered.The microbioreactor,constructed with polydimethylsiloxane(PDMS),has the format of a standard 96-w ell cell culture plate and is perfused using silicone tubing via a multi-channel peristaltic pump or multiple syringe pumps[10].The bioreactor geometry can be modi fied so that the silicone tubing serving as the inlet and outlet ports can be arranged in different styles—two of which are explored in this study.Fig.2 show s a schematic diagram,as w ell as a photograph,of Tissue Flex®with 12 microbioreactors.Each microbioreactor has a dimension of 6.6 mm×11 mm.For the purposes of this study, fluid flow and mass transport in only one microbioreactor was considered.

2.2.Scaffold and cells

In thisinvestigation,wesimulated masstransport within two 3Dcell culture constructs,modelled as a 1 mm thick porous slab structure and as a porous bead of diameter 1 mm,both synthesised using alginate.Scaffold porosity and permeability are regulated by a multitude of factors,which include concentration of alginate and cross-linking solutions,method of synthesis,and,eventually,the pore size.As such,there is a w hole array of case specific porosity and permeability values that can be introduced in the model.Scaffold porosity in excess of 90%can be easily achieved.Furthermore,glucose diffusivity in alginate,proportional to its porosity,can be as high as 90%[28].As such,both slab and spherical scaffolds were assigned isotropic porosity of 85%.As permeability is rather difficult to characterise there was lack of reasonably consistent values.After carefully review ing the work conducted by Julian et al.w e assigned the tw o scaffolds permeability of 10-10m2[29].

Alginate was considered in this analysis due to its wide application[30]in synthesis of micro-carriers employed to immobilise cells due to its inertness,biocompatibility,high porosity,and amenability to various preparation methodologies[28,30-33].Slab and sphere morphologies were modelled due to their ease of preparation and,as such,pervasive application.Scaffold dimensions were based on ease of synthesis and,therefore,widespread utility.The simplest way to create the spherical shape entails transferring alginatesolution through a syringe,which results in beads roughly equal to or greater than 1 mm.As this technique involving syringes is inexpensive,simple,commonly used in cellculture laboratories,the diameter of the spherical scaffold was set to 1 mm.The height of the slab was limited to 1 mm as the resulting volume provides optimum growing space enabling cell expansion without presenting,in itself,diffusional limitations.

Fig.1.Bioreactor and scaffold con figurations employed in this investigation.The figure shows the two bioreactor as well as scaffold con figurations used in this study.The geometry on the left is referred as top-in out whereas the one on the right as symmetrical.Bioreactor dimensions are also listed in the figure.Solid arrow s(near the ports)indicate the direction of medium flow.The two scaffold morphologies,along with their dimensions,are also shown:slab(left)and bead(right).Each scaffold was assigned porosity of 85%.

Fig.2.Tissue Flex®Microbioreactos.The photograph and schematic diagram of Tissue Flex®micro biore actors is shown.The schematic represents the microbioreactors being operated in a parallel set-up.In the figure,twelve bioreactors are being supplied with culture medium(employing a multi-channel peristaltic pump),and the effluent being collected individually.The schematic was reprinted from Ref.[10](c)(2007)Elsevier.Photograph courtesy:Zyoxel Ltd.

The metabolic behaviour of human mesenchymal stem cells(hMSCs)was simulated in this study,with glucose modelled as the nutrient being transported to the cells,which were encapsulated within the two scaffolds.As w e w anted to investigate the maximal load under which the bioreactor can deliver optimally,two static cell densities were considered in the model:1 million·ml-1and 10 million·ml-1of the cell suspension.The two cell densities represented the typical and extreme cell densities for cell therapy and tissue engineering applications.As such,cell grow th was not considered in the model.Therefore,cells were assumed to have been encapsulated homogeneously throughout the two scaffolds.This is equivalent to the initial culture conditions and the nutrient transport would decide the survivability of the encapsulated cells.

Each cell was assumed to consume glucoseat azero-order consumption rate of 270 fmol·L-1·h-1·cell-1[34].Glucose diffusivity in alginate and water at 37 °C were considered to be 6.59 × 10-10m2·s-1[35]and 9.3 × 10-10m2·s-1[35,36],respectively.h MSCs were modelled as sinks within the slab and the bead,consuming glucose at a set rate,based on the values of glucose consumption and volumetric cell count mentioned above.The variables investigated are listed in Table 1.

2.3.Nutrient medium

Glucose concentrations of 4.5 g·L-1and 1 g·L-1were considered for analysis.This was done for practical purposes as a nutrient medium most commonly used for cell culture,Dulbecco's Modified Eagle Medium(DMEM),contains4.5 g·L-1glucose(high concentration).For practical reasons,as recommended by the manufacturer of Tissue Flex®,Zyoxel Ltd,media inlet rate of 25 μl·h-1was utilised.To compare its efficacy and efficiency,an inlet rate of 100 μl·h-1wasalso investigated.A common practice while culturing cells is the use of Foetal Bovine Serum(FBS)as a supplement to aid cell survival,grow th,and proliferation.While the addition of FBS in DMEM may result in the fluid behaving in a non-New tonian manner,the overall concentration of serum generally added is not concentrated enough to alter the flow characteristics of DMEM.Therefore,the fluid phase was assumed to be Newtonian.

2.4.Modelling framework and governing equation

In silico bioreactor geometries were constructed using a CAD/meshing software platform,CFD-GEOM(ESI GROUP,Paris,France).The bioreactor geometry was then meshed to create finite volumes(or control volumes),where fluxes are calculated,along with discrete locations w here the variables are defined.In this formulation of the finite volume method,all variables(velocities,pressure and concentrations)are defined on the same location on the grid(cell centre),resulting thus in a collocated mesh formulation.Unstructured tetrahedral meshes were used for this study,since they allow for great flexibility and automation in mesh generation,especially in complex geometries.Unstructured meshes introduce ease in mesh generation but imply a requirement for a larger number of elements,w hen compared to structured hexahedral meshes for example,to achieve the same level of accuracy.This requirement was indeed met by the resolutions examined and employed,as w e shall discuss in the Grid Independence Section of this paper.

CFD-ACE+(ESI GROUP,Paris,France)was used to formulate the model representing the bioreactor system and to solve the discretised governing equations.Flow within the bioreactor was represented by the continuity and Navier-Stokes equations:

The following modified continuity and momentum equations were used to handle flow inside the porous scaffolds:

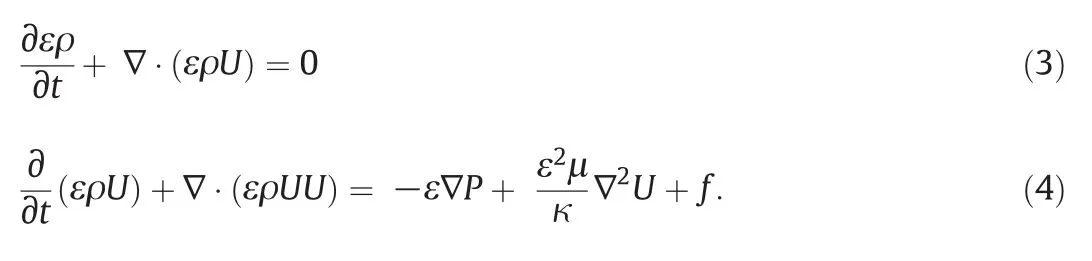
The spatial distribution of glucose,represented by C in Eq.(5),inside the bioreactor was described by:

CFD-ACE+primarily solves the general transport equation,Eq.(6),which captures the basic conservation law s of interest.Additional parameters needed(diffusivities,viscosity,density)are all set to constants,as is the case with the common DMEM medium used in cell cultures(Newtonian incompressible fluid).Therefore,the generalised transport equation for a conserved quantity Φ is given by:

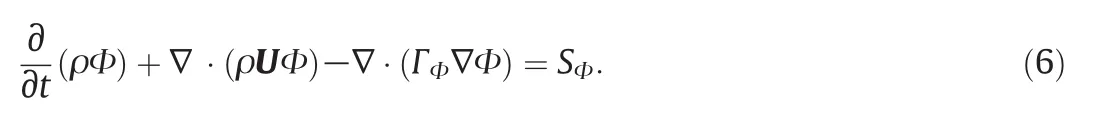
In this equation,ρ represents the fluid density and U the velocity vector.This equation is integrated over the control volumes described above;subsequently the divergence theorem is applied,converting volume quantities to surface fluxes and ensuring a conservative formulation of the discretised equations,as show n in Eq.(7):

In Eq.(7),Srepresentsany of the faces of the control volume,whereas nSis the unit vector normal to that surface.

As w e were interested in evaluating bioreactor performance while operating at full capacity,a zero-order overall cell consumption rate was assumed,which can be expressed as s×d,w here s is the consumption rate for a single cell and d is the cell density.As a result the cell grow th rate,practically zero,did not depend upon glucose concentration.Furthermore,the model did not rely on any chemical reactions involving glucose or any other chemical substrate.The model,therefore,did not consider any additional kinetic model;the consumption of glucose by cells was accounted for by assigning appropriate spatially distributed sink terms in the transport equations,thus accounting for consumption,as w e quantify in the sequel.

The values of relevant quantities(e.g.Φ)inside the control volumes were determined by employing a central,second order,differencing scheme.The transport equations were solved in their full transient form.A variant of the Crank-Nicolson scheme,again second order,was employed to march the discretised equations in time and ensure temporal accuracy.The segregated solver we employed(i.e.solving for the different variables one after the other and iterating to convergence)necessitates special handling of the continuity and pressure(we remind the reader that pressure does not appear in the conservation of mass equation).To achieve the simultaneous evaluation of the pressure field,w e employed the inherently iterative Semi-Implicit for Pressure-Linked Equations Consistent(SIMPLEC)scheme[37],an adaptation of the Semi-Implicit for Pressure-Linked Equations(SIMPLE)method[38],to couple the pressure and velocity fields by introducing anew variable,the pressure correction,and solving for that variable to improve upon an initial pressure field,till convergence.

The aforementioned sets of equations result in pseudo-linear sparse systems of equations that have to be solved,at least to partial convergence,within each iteration.We chose to use the Algebraic Multi Grid(AMG)scheme for this,a method that offers rapid convergence by creating a succession of coarser and finer grids and injecting or interpolating solutions from onegrid refinement level to the other,thus achieving the reduction of multiple wavelengths of error(proportional to average cell size)simultaneously[39].

Domains with different properties(like,for example,the porous cell-seeded regions)were accounted for by creating a multi-block mesh structure;each block with its own topology and connectivity.In the case of this study,two blocks were always used.A higher order interpolation arbitrary interface method was used on the common surface of the two blocks,ensuring continuity of the solution variables across this interface.

Dirichlet(in flow and w alls)and Neumann boundary conditions were applied as required.The time step used in the simulations was 450 s,but other, finer,time step values of 50s,150 s,300 s were used to con firm time step independence.Each time step required between 200-500 iterations to reach satisfactory convergence.In this set of simulations a drop of eight to ten orders of magnitude of residuals was show n to be adequate.Finally,the code was executed in parallel on 8 cores(Intel Xeon,clocked at 2.66 GHz),using the MPI protocol and domain decomposition.

2.5.Grid independence analysis

A detailed grid sensitivity analysis was conducted on one of the test cases to ensure convergence and independence of the results obtained from numerical parameters.The test cases examined involved structured(50000;100000;200000 and 400000 elements)as well as unstructured(100000 and 400000 elements)meshes.The mesh independence study show ed excellent convergence,with the finest grids(200000 and 400000 elements structured and 400000 elements unstructured)yielding practically indistinguishable results.We opted to use unstructured tetrahedral meshes with 400000 elements,for the reasons mentioned above( flexibility and automation).This came at a cost of approximately×2.5 in computational time,w hen compared to the coarsest fully resolved structured mesh(200000 elements),a cost that we believe was justified by the rapid turnaround time in mesh generation that the unstructured option offers.The importance of the unstructured mesh flexibility in this model warrants an additional comment:The geometry employed in this investigation consisted of multiple sub-components(the bioreactor,the port(s),and the scaffold).As streamlines and transport gradients vary the most near component interfaces and construct surfaces,these regions were assigned very fine grid structure.Unstructured meshes have the advantage that no implicit structure of co-ordinate lines is imposed by the grid.As such,the mesh can be easily concentrated only w here necessary,without was ting computer storage and introducing unnecessary elements.Away from the regions mentioned above,cell size was increased without loss of accuracy.Unless otherwise noted,unstructured tetrahedral meshes with 400000 elements were used.

3.Results

3.1.Impact of alginate morphologies

Given that the slab con figuration of thickness 1 mm contained(about two orders of magnitude)more cells compared with the spherical scaffold of diameter 1 mm,nutrient demand was higher in the former.This is evident from Figs.3 and 4 that show the glucose distribution at a distance of 10 μm from the bottom in the slab and in the middle of the alginate sphere,respectively.This is made particularly apparent if glucose concentration is compared after the system has achieved steady state.In Fig.5,noticethe steady state glucose concentrations in the alginate slab and bead;while both are sufficiently high to ensure adequate nutrition,the drop in the alginate slab is higher.The default boundary conditions recommended for the microbioreactor,listed in Table 2 as case I,seem to be sufficient to carry out glucose transport to the innermost layer of cells seeded in both the slab,as w ell as the spherical scaffold.The data indicate that when steady state is achieved,the system remains capable of supporting cell expansion and maintaining cell viability.This is achieved by ensuring that at least 10%of the initial glucose concentration(2.5×10-6kM)is still avail able to the innermost regions of a cell culture.

Fig.3.Time evolution of glucose concentration at the bottom of the alginate slab.A comparison of glucose concentrations computed at a distance of 10 μm from the bottom in the slab con figuration perfused under the different boundary conditions.The figure show s glucose concentration as measured on a transverse section of the scaffold made 10μm from the bottom of the slab.The two biore actor con figurations shown on the right end of the figured is play the boundary conditions as well as the site of glucose measurement.Arrow sindicate the direction of medium flow.All other cases,apart from III and(partially)V(for reasonsd is cussed),meet the criteri are quired to ensure cellviability for any duration of time.Glucose concentration was measured in kM.

Fig.4.Time evolution of glucose concentration in bioreactors containing the spherical scaffold.A comparison of glucose concentrations computed at the centre of the alginate bead perfused under the various boundary conditions.The figure shows glucose concentration as measured on a frontal section made at the centre of the bioreactor.The two bioreactor configurations show n on the right end of the figure display the boundary conditions as well as the site of glucose measurement.Arrow s indicate the direction of medium flow.All test cases seem to meet the criteria to ensure cell viability for any duration of time,as the glucose consumption requirements,compared to the slab,are quite low.Glucose concentration was measured in kM.

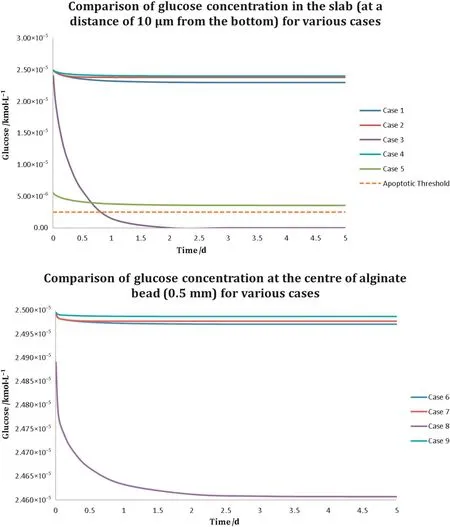
Fig.5.Comparison of glucose concentration in the slab vs.spherical scaffold.(Top)The figure compares glucose concentration at a distance of 10 μm(from the bottom)in the slab as the system achieves steady state.(Bottom)The figure compares glucose concentration at the centre of the alginate bead as the system achieves steady state.The figure at the bottom doesnot indicate the apoptotic threshold as all con figurations with alginate bead performed substantially above that threshold.

Table 2 Various test cases and relevant boundary conditions utilised in this investigation.

3.2.Impact of flow-rate

Asreported above,the default flow-rate of 25μl·h-1was found suitable to sustain h MSCculturesoperating at full capacity by ensuring supply of adequate amount of glucose to the innermost scaffold regions in both morphologies.Cases II and VII represent computations w here the nutrient media inlet velocity was increased by a factor of four,to 100 μl·h-1.Unsurprisingly,the increased flow-rate,as can be observed in Figs.3,4,and 5,led to a far improved distribution and supply of glucose within the slab and bead morphologies.

3.3.Impact of cell density

While w e found the standard recommended flow-rate optimal for cell grow th for the recommended 1 million·ml-1cell suspension density,it,however,fails if cell density of 10 million cells·ml-1suspension(case III)is used,as evident by a rapid decline in glucose concentration within the slab.Here,glucose concentration plummeted w ell below the critical concentration(10%of the initial value)within the first 24 h,indicating that necrosis will set in soon after,in case the flow rate is not altered.The drop in glucose concentration within the spherical scaffold encapsulating the higher cell density was observed to be the largest across cases involving the alginate bead.How ever,with the total cell count within the bead still quite low,transport across the bead was found adequate to sustain the expansion and viability of the encapsulated cells.

3.4.Impact of bioreactor con figuration

Similarly,data obtained for the alternative bioreactor con figuration(top-inout,cases IV and IX)indicated that the boundary conditions are sufficient to ensurethat even the innermost cellscontinue to receive at least the critical concentration of glucose at all times;refer to Figs.3 and 4.How ever,rather surprisingly,the performance of the top-inout con figuration with media inlet velocity of 25 μl·h-1,outperformed the default boundary conditions(cases I and VI)as well as cases III and VII w here the symmetrically organised ports were perfused with mediainlet velocity of 100 μl·h-1.This is best evident in Fig.5,especially for alginate bead,w here the drop in glucose concentration within the top-inout con figuration was recorded to be the smallest.This observation underpins the importance of analysing transport phenomena and flow in such reactors rigorously and using detailed first-principles methodologies to quantify the bioreactor's fluid mechanics.

3.5.Impact of nutrient media

When low concentration glucose media(1 g·L-1,case V)was utilised,although the overall glucose concentration in the bioreactor stayed above the critical concentration(as can be seen in Fig.5),the analysis suggests that the standard recommended flow rate may lead to sub-optimal distribution of glucose(at least in the physical scenario w here proliferation of cells and the act of matrix deposition by them will alter the permeability of their immediate microenvironment).The use of low concentration glucose medium had no negative impact on the spherical scaffold.

3.6.Shear distribution

As show n in Figs.6 and 7,the resulting shear stresses in all the test cases were on the low er end of the scale and physiologically neutral,with the maximum stress being 10-6Pa(cases IV and IX)follow ed by 10-7Pa(cases III and VIII).Shear stress was calculated at the stop surface of both scaffolds,which is 1 mm from the bottom end of the bioreactor(refer to Figs.6 and 7),along an imaginary line/plane running across the two scaffolds.Shear stress for all the cases evaluated was found to be highest at the top w here the alginate scaffold was fully exposed to the perfusion medium,with shear being almost the same in the middle and close to the bottom for the slab.This,how ever,was not true for cases with the spherical scaffold w here the low est stress was observed in the middle.For cases involving the slab construct,shear stress dropped by three orders of magnitude bet ween the middle and top.Furthermore,as can be observed in Fig.7,shear stress in the top-inout configurations was observed to be higher than their symmetrical counterparts for the same media inlet velocity(25 μl·h-1).

4.Discussion

In an investigation by Carrier et al.[40],it was observed that in a culture of cardiac cells the region beyond alayer of 100μm thick cellscould not be supported via diffusion under static conditions.In vivo,cells are generally located no more than approximately 100 μm[41]from capillaries that supply them with oxygen and nutrients,such as glucose.A feature central to the functionality of bioreactors is their ability to carry out mass transport so as to maintain cell viability within 3D cultures[41].Similarly,shear stress has been implicated in influencing mammalian cell differentiation,as well as pattern and quality of growth.For example,endothelial cells tend to orient themselves in the flow direction[42];shears of approximately 0.01 Pa have been found to be ideal for cell grow th[43];and application of shear stress can influence MSC fate[44-46].Unlike unicellular organisms,animal cells tend to have low tolerance to fluid forces which rule out high nutrient flow rates that,despite achieving sufficient mass transport,may create fluid flow patterns leading to high shear stresses[47].With the exception of cells present in tissues that are exposed to significant haemodynamic loading,such as endothelial(direct loading)or smooth muscle cells(indirect loading),the majority of cells in the human body do not experience high shears[41,47].As a result,they react differently to shear stresses in vitro.Dow n-regulation of endothelial cell proliferation under laminar flow(steady shear stress conditions)and up-regulation of survival factors,such as Kruppel-like factor-2,while the cells experience both pulsatile and reciprocating oscillating flow[48];development of a fibrous capsule in chondrogenic cell-matrix constructs w hen exposed to turbulent flow conditions[49];and increased mineralised deposition in osteoblasts due to enforced differentiation as a result of long-term exposure to shear stress[50-53]are but a few examples.Therefore,if designed properly, fluid dynamics inside a bioreactor can be exploited to either initiate desired cellular differentiation processes or enhance cell proliferation,expansion,and attachment[41,47,54,55].A bioreactor that utilises pulsatile flow to fabricate cardiovascular patch tissues is a perfect example w here this concept was successfully utilised[56].

Fig.6.Comparison of shear stress observed in bioreactors with different con figurations and flow regimes.Acomparison of shear stress observed at a distance of 1 mm from the bottom(the top of the cellular slab and the alginate bead),in the symmetrical bioreactor for three different boundary conditions:inlet rate of 25 μl·h-1,inlet rate of 100 μl·h-1,and the top-inout con figuration.Figure at the top captures the shear stress observed at the top of the slab con figuration.The horizontal axis represents the length/diameter of the slab/bead.Although shear stress for all three boundary conditions observed was physiologically ineffective,shear stress observed for the “top-inout”con figuration,achieved at a flow rate of 25 μl·h-1,was the highest.

The results obtained are consistent with the expected behaviour of Tissue Flex®,along with alginate,high-glucose DMEM,as w ell as the media flow-rate in terms of supporting perfused expansion of h MSCs.In addition to efficient glucose transport,laminar flow within the bioreactor resulted in low,physiologically neutral,shear environment for encapsulated cells.This constitutes a very useful piece of information,for low shear environments can play an augmentative role in tissue formation by inducing and facilitating cell-cell contact and cell aggregation,as well as cell-matrix associations[57].High shear stresses,though,can disrupt the process of cell expansion creating micro-pockets that may result in gradients or gaps within the growing cell colonies compromising the homogeneity of resulting cell population.These boundary conditions,how ever,cannot be used when employing the slab morphology to either seed the higher cell density(10 million cells·ml-1of cell suspension)or deliver low-glucose DMEM(1 g·L-1).In both cases,especially the former,a rapid decline in glucose concentration was observed that could potentially result in cell death or differentiation due to glucose depletion.Glucose distribution in the spherical morphology,how ever,due to low transport requirements,wasnot affected by any of the tested parameters.

Fig.7.Visualisation of shear stress in the three cases discussed in Fig.6.Shear Stress observed on the top(approximately 1 mm from the bottom)of slab and alginate sphere for three cases.

The most interesting result to emerge from this investigation was the performance of the top-inout con figuration in terms of both glucose transport as w ell as shear.Perfused with media inlet rate of 25 μl·h-1,the top-inout con figuration resulted in a more efficient transport of glucose,in comparison with the symmetrical con figuration perfused with media inlet rate of 100 μl·h-1.Additionally,an increase in shear stress by two orders of magnitude for the bioreactors containing the slab,and by an order of magnitude for the bioreactors containing the bead(for the same media inlet rate)was also observed.This piece of data has significant design implications,for it suggests that shear dependent differentiation can be induced by modifying bioreactor design to generate physiologically relevant shear stressat a laminar media inlet rate.As such,a variety of designs can be tested using CFD prior to the construction.This reinforces the significance of CFD as an investigative tool in general,and is a testament to CFD's strength as a concept selection and design optimisation tool.

5.Conclusions

The default recommended con figuration and operational parameter ranges of the Tissue Flex®microbioreactor are shown to maintain glucose transport and shear stress levels that are suitable for cell survival and proliferation.The microbioreactor can,therefore,provide the cells with a micro environment conducive to their grow th and expansion.Mass transport analysis on other nutrients,grow th factors,and metabolites can be conducted similarly.The parameters considered in this analysis were based on their practical utility.For example:the shape and dimensions of the bioreactor were based on the wells of a 96-well cell culture plate,concentration of glucose based on a commonly available nutrient medium,the choice of scaffold material,morphology,and dimensions were based on ease of preparation,and cell phenotype on the more widely employed cell types because of their robustness,plasticity,and ease of availability.Furthermore,the evidence that low media inlet rates can lead to higher shear by varying bioreactor con figuration proves how CFD can be employed to design bioreactors to expose cells to physiologically relevant shear at laminar flow rates.

Nomenclature

Conflict of Interest Disclosure

Prof Zhanfeng Cui,the corresponding author on this article,is the academic founder and a non-executive director of Zyoxel Ltd,a spin off company of the University of Oxford.Zyoxel commercialises Tissue Flex®microbioreactors as part of its business.The computations in this investigation are based on the dimensions of Tissue Flex®microbioreactor.

Acknowledgements

The authors are grateful to Dr M.Megahed and the ESI Group for allowing the use of the CFD-ACE multiphysics platform.Himanshu Kaul gratefully acknow ledges financial support through a Department of Engineering Science,University of Oxford,Scholarship.

[1]R.Langer,J.P.Vacanti,Tissue Engineering,Science 260(1993)920-926.

[2]J.R.Fuchs,B.A.Nasseri,J.P.Vacanti,Tissue engineering:A 21st century solution to surgical reconstruction,Ann.Thorac.Surg.72(2001)577-591.

[3]A.Khademhosseini,R.Langer,Microengineered hydrogels for tissue engineering,Biomaterials 28(2007)5087-5092.

[4]H.Mertsching,J.Hansmann,Bioreactor Technology in Cardiovascular Tissue Engineering,in:C.Kasper,M.van Griensven,R.Portner(Eds.),Bioreactor Systems for Tissue Engineering,Springer,Berlin 2009,pp.29-37.

[5]E.S.Place,N.D.Evans,M.M.Stevens,Complexity in biomaterials for tissue engineering,Nat.Mater.8(2009)457-470.

[6]D.Wendt,S.Riboldi,M.Cioffi,I.Martin,Bioreactors in Tissue Engineering:Scientific Challenges and Clinical Perspectives,in:C.Kasper,M.van Griensven,R.Portner(Eds.),Bioreactor Systems for Tissue Engineering,Springer,Berlin 2009,pp.1-27.

[7]S.Visw anathan,P.W.Zandstra,Tow ards predictive models of stem cell fate,Cytotechnology 41(2003)75-92.

[8]J.A.Burdick,G.Vunjak-Novakovic,Engineered microenvironments for controlled stem cell differentiation,Tissue Eng.Part A 15(2009)205-219.

[9]I.Freshney,B.Obradovic,W.Grayson,C.Cannizzaro,G.Vunjak-Novakovic,Principles of tissue culture and bioreactor design,in:R.Lanza,R.Langer,J.Vacanti(Eds.),Principles of Tissue Engineering,Academic Press,San Diego 2007,pp.155-184.

[10]Z.F.Cui,X.Xu,N.Trainor,J.T.Triffitt,J.P.G.Urban,U.K.Tirlapur,Application of multiple parallel perfused microbioreactors and three-dimensional stem cell culture for toxicity testing,Toxicol.In Vitro 21(2007)1318-1324.

[11]I.Martin,T.Smith,D.Wendt,Bioreactor-based roadmap for the translation of tissue engineering strategies into clinical products,Trends Biotechnol.27(2009)495-502.

[12]H.Singh,D.Hutmacher,Bioreactor studies and Computational Fluid Dynamics,in:C.Kasper,M.van Griensven,R.Portner(Eds.),Bioreactor Systems for Tissue Engineering,Springer,Berlin 2009,pp.231-249.

[13]M.N.Cinbiz,R.S.Tigli,I.G.Beskardes,M.Gumusderelioglu,U.Colak,Computational fluid dynamics modeling of momentum transport in rotating w all perfused bioreactor for cartilage tissue engineering,J.Biotechnol.150(2010)389-395.

[14]L.Freed,G.Vujnak-Novakovic,Tissue Engineering Bioreactors,in:R.Lanza,R.Langer,J.Vacanti(Eds.),Principles of Tissue Engineering,Academic Press,San Diego 2000,pp.143-156.

[15]A.R.Patrachari,J.T.Podichetty,S.V.Madihally,Application of computational fluid dynamics in tissue engineering,J.Biosci.Bioeng.114(2012)123-132.

[16]H.Kaul,Z.Cui,Y.Ventikos,A multi-paradigm modeling framework to simulate dynamic reciprocity in a bioreactor,PLoS One 8(2013)e59671,http://dx.doi.org/10.1371/journal.pone.0059671.

[17]M.J.Song,D.Dean,M.L.K.Tate,In situ spatiotemporal mapping of flow fields around seeded stem cells at the subcellular length scale,PLoS One 5(2010)e12796,http://dx.doi.org/10.1371/journal.pone.0012796.

[18]M.Ciof fi,F.Boschetti,M.T.Raimondi,G.Dubini,Modeling evaluation of the fluid-dynamic microenvironment in tissue-engineered constructs:A micro-CT based model,Biotechnol.Bioeng.93(2006)500-510.

[19]F.Maes,P.van Ransbeeck,H.van Oosterw yck,P.Verdonck,Modeling Fluid Flow Through Irregular Scaffolds for Perfusion Bioreactors,Biotechnol.Bioeng.103(2009)621-630.

[20]B.Bilgen,G.A.Barabino,Location of scaffolds in bioreactors modulates the hydrodynamic environment experienced by engineered tissues,Biotechnol.Bioeng.98(2007)282-294.

[21]K.A.Williams,S.Saini,T.M.Wick,Computational fluid dynamics modeling of steadystate momentum and mass transport in a bioreactor for cartilage tissue engineering,Biotechnol.Prog.18(2002)951-963.

[22]F.Consolo,G.B.Fiore,S.Truscello,M.Caronna,U.Morbiducci,F.M.Montevecchi,A.Redaelli,A computational model for the optimization of transport phenomena in a rotating hollow- fiber bioreactor for arti ficial liver,Tissue Eng.Part C 15(2009)41-55.

[23]M.T.Raimondi,F.Boschetti,L.Falcone,F.Migliavacca,A.Remuzzi,G.Dubini,The effect of mediaperfusion on three-dimensional cultures of human chondrocytes:Integration of experimental and computational approaches,Biorheology 41(2004)401-410.

[24]F.Boschetti,M.T.Raimondi,F.Migliavacca,G.Dubini,Prediction of the micro- fluid dynamic environment imposed to three-dimensional engineered cell systems in bioreactors,J.Biomech.39(2006)418-425.

[25]P.Yu,T.Lee,Y.Zeng,H.T.Low,A 3D analysis of oxygen transfer in a low-cost microbioreactor for animal celll suspension culture,Comput.Methods Prog.Biomed.85(2007)59-68.

[26]H.Singh,S.H.Teoh,H.T.Low,D.W.Hutmacher,Flow modelling w ithin a scaffold under the in fluence of uni-axial and bi-axial bioreactor rotation,J.Biotechnol.119(2005)181-196.

[27]T.Yi-Chin,Z.Chi,Z.Jing,K.Yuet Mei,C.Shi,V.D.Samper,D.van Noort,D.W.Hutmacher,H.Yu,A novel 3D mammalian cell perfusion-culture system in micro fluidic channels,Lab Chip 7(2007)302-309.

[28]J.J.Casciari,S.V.Sotirchos,R.M.Sutherland,Glucose diffusivity in multicellular tumor spheroids,Cancer Res.48(1988)3905-3909.

[29]J.A.Teixeira,M.Mota,A.Venancio,Model identi fication and diffusion coef ficients determination of glucose and malic acid in calcium alginate membranes,Chem.Eng.J.56(1994)B9-B14.

[30]O.Smidsrod,G.Skjakbraek,Alginate as immobilization matrix for cells,Trends Biotechnol.8(1990)71-78.

[31]T.N.Julian,G.W.Radebaugh,S.J.Wisniewski,Permeability characteristics of calcium alginate films,J.Control.Release 7(1988)165-169.

[32]J.E.Melvik,M.Dornish,Alginate as a carrier for cell immobilisation,in:V.Nedovic,R.Willaert(Eds.),Fundamentals of Cell Immobilisation Biotechnology,8A,Springer,Dordrecht 2004,pp.33-51.

[33]M.Khalil,A.Shariat-Panahi,R.Tootle,T.Ryder,P.McCloskey,E.Roberts,H.Hodgson,C.Selden,Human hepatocyte cell lines proliferating as cohesive spheroid colonies in alginate markedly upregulate both synthetic and detoxi ficatory liver function,J.Hepatol.34(2001)68-77.

[34]W.R.Gombotz,S.F.Wee,Protein release from alginate matrices,Adv.Drug Deliv.Rev.31(1998)267-285.

[35]C.H.Goh,P.W.S.Heng,L.W.Chan,Alginates as a useful natural polymer for microencapsulation and therapeutic applications,Carbohydr.Polym.88(2012)1-12.

[36]G.Pattappa,H.K.Heyw ood,J.D.de Bruijn,D.A.Lee,The metabolism of human mesenchymal stem cells during proliferation and differentiation,J.Cell.Physiol.226(2011)2562-2570.

[37]J.P.van Doormaal,G.D.Raithby,Enhancements of the simple method for predicting incompressible fluid- flows,Numer.Heat Transfer 7(1984)147-163.

[38]S.V.Patankar,D.B.Spalding,Calculation procedure for heat,mass and momentumtransfer in 3-dimensional parabolic flow s,Int.J.Heat Mass Transfer 15(1972)1787-1806.

[39]B.R.Hutchinson,P.F.Galpin,G.D.Raithby,Application of additive correction multigrid to the coupled fluid flow equations,Numer.Heat Transfer 13(1988)133-147.

[40]R.L.Carrier,M.Rupnick,R.Langer,F.J.Schoen,L.E.Freed,G.Vunjak-Novakovic,Perfusion improves tissue architecture of engineered cardiac muscle,Tissue Eng.8(2002)175-188.

[41]P.Vermette,Y.Martin,Bioreactors for tissue mass culture:Design,characterization,and recent advances,Biomaterials 26(2005)481-503.

[42]B.Imberti,D.Seliktar,R.M.Nerem,A.Remuzzi,The response of endothelial cells to fluid shear stress using a co-culture model of the arterial w all,Endothelium 9(2002)11-23.

[43]S.H.Mardikar,K.Niranjan,Observations on the shear damage to different animal cells in a concentric cylinder viscometer,Biotechnol.Bioeng.68(2000)697-704.

[44]T.M.Maul,D.W.Chew,A.Nieponice,D.A.Vorp,Mechanical stimuli differentially control stem cell behavior:morphology,proliferation,and differentiation,Biomech.Model.Mechanobiol.10(2011)939-953.

[45]K.Yamamoto,T.Takahashi,T.Asahara,N.Ohura,T.Sokabe,A.Kamiya,J.Ando,Proliferation,differentiation,and tube formation by endothelial progenitor cells in response to shear stress,J.Appl.Physiol.95(2003)2081-2088.

[46]G.Yourek,S.M.McCormick,J.J.Mao,G.C.Reilly,Shear stress induces osteogenic differentiation of human mesenchymal stem cells,Regen.Med.5(2010)713-724.

[47]B.Weyand,M.Israelowitz,H.von Schroeder,P.Vogt,Fluid Dynamics in Bioreactor Design:Considerations for the Theoretical and Practical Approach,in:C.Kasper,M.van Griensven,R.Portner(Eds.),Bioreactor Systems for Tissue Engineering,Springer,Berlin 2009,pp.251-268.

[48]S.Chien,Mechanotransduction and endothelial cell homeostasis:the wisdom of the cell,Am.J.Physiol.Heart Circ.Physiol.292(2007)H1209-H1224.

[49]G.Vunjak-Novakovic,L.Meinel,G.Altman,D.Kaplan,Bioreactor cultivation of osteochondral grafts,Orthod.Craniofacial Res.8(2005)209-218.

[50]M.R.Kreke,W.R.Huckle,A.S.Goldstein,Fluid flow stimulates expression of osteopontin and bone sialoprotein by bone marrow stromal cells in a temporally dependent manner,Bone 36(2005)1047-1055.

[51]V.I.Sikavitsas,G.N.Bancroft,H.L.Holtorf,J.A.Jansen,A.G.Mikos,Mineralized matrix deposition by marrow stromal osteoblasts in 3D perfusion culture increases with increasing fluid shear forces,Proc.Natl.Acad.Sci.U.S.A.100(2003)14683-14688.

[52]Y.C.Wang,T.Uemura,R.Dong,H.Kojima,J.Tanaka,T.Tateishi,Application of perfusion culture system improves in vitro and in vivo osteogenesis of bone marrowderived osteoblastic cells in porous ceramic materials,Tissue Eng.9(2003)1205-1214.

[53]X.J.Yu,E.A.Botchw ey,E.M.Levine,S.R.Pollack,C.T.Laurencin,Bioreactor-based bone tissue engineering:The in fluence of dynamic flow on osteoblast phenotypic expression and matrix mineralization,Proc.Natl.Acad.Sci.U.S.A.101(2004)11203-11208.

[54]C.Y.J.Ma,R.Kumar,X.Y.Xu,A.Mantalaris,A combined fluid dynamics,mass transport and cell growth model for a three-dimensional perfused biorector for tissue engineering of haematopoietic cells,Biochem.Eng.J.35(2007)1-11.

[55]L.D.Garza-Garcia,L.M.Carrillo-Cocom,D.Araiz-Hernandez,P.Soto-Vazquez,J.Lopez-Meza,E.J.Tapia-Mejia,S.Camacho-Leon,E.Garcia-Lopez,C.A.Rodriguez-Gonzalez,M.M.Alvarez,A biopharmaceutical plant on a chip:continuous micro-devices for the production of monoclonal antibodies,Lab Chip 13(2013)1243-1246.

[56]R.Sodian,T.Lemke,M.Loebe,S.P.Hoerstrup,E.V.Potapov,H.Hausmann,R.Meyer,R.Hetzer,New pulsatile bioreactor for fabrication of tissue-engineered patches,J.Biomed.Mater.Res.58(2001)401-405.

[57]B.R.Unsw orth,P.I.Lelkes,Grow ing tissues in microgravity,Nat.Med.4(1998)901-907.