Asymmetric breakup of a droplet in an axisymmetric extensional flow☆

Dongming Yu ,Manman Zheng ,Taoming Jin ,Jingtao Wang ,*

1.Introduction

In the dispersion process of immiscible liquids,the breakup of drops plays a critical role to determine the size distribution of drops.This issue is of major importance in heterogeneous reactions,liquid-liquid extractions,oil-water separation,emulsion polymerization and other applications that require multiphase mixing[1-3].Thus,a better understanding of the physical mechanisms of drops breakup would be very important for these unit operations in chemical industries.It will be helpful to solve the problems involving mass transfer and heat transfer between different phases,especially,it is critical to predict the drop size distribution.

Since the pioneer work by Taylor[4]w ho invented the four-roll mill to generate flow fields to study the rheology of a single droplet,extensive researches have been done to investigate,theoretically,experimentally and numerically,the deformation and breakup of droplets under the shears of external flow s both in in finite media and in con fined geometries[5-10].Among these works,in finite extensional flow s[5-7]and hyperbolic flow s in cross hydrodynamic traps[8]are employed to study the effects of viscosity ratios,inter facial tensions and capillary numbers Ca on the deformation and breakup since droplets trapped at the stagnant points are naturally deformed by the flow shears.When Ca is below a critical value Cac,the droplet will finally reach an equilibrium shape;when Ca＞Cac,the droplet will break up into two daughter droplets.

How ever,most of the works concentrate on symmetric deformation and breakup[5,6,11].Actually,asymmetric deformation and breakup always occur naturally in the macroscopic dispersion of immiscible liquids in a stirred tank.Even in an experiment which particularly studies the rheology of a single droplet in a symmetric flow field,it is very hard to locate(keep)the droplet at the exact balance point[4,12].Recently,droplet-based micro fluidics(also called digital micro fluidics)technology has been developed rapidly,w hose major advantage is to generate droplets with monodispersity[13].Based on these droplets,diverse precise manipulations could be done in order to achieve various purposes,such as the fabrication of nonspherical polymer particles,microcapsules,spherical photonic crystals,and so on[14,15].In 2004,Link and co-workers[9]successfully broke the droplet into two daughter droplets with unequal sizes through T-junctions with two side arms of unequal lengths,which verified very w ell that the asymmetric geometry of microchannels could generate an asymmetric flow field and result in the asymmetric deformation and breakup of droplets.After that,various devices have been designed to study the asymmetric rheology behaviors of droplets in con fined geometries,such as bifurcating channel[16],asymmetric T junction[17],Y junctions[16],obstacles[18,19]etc.In 2013,Salkin and co-w orkers[20]investigated the fragmentation of isolated slugs against rectangular obstacles and asymmetric loops.They found that a critical capillary number(Cac)was needed to break a slug.Only above Cac,the slug could be broken into two small daughter slugs.A mean- field approximation was introduced to predict the volume ratio of the two daughter slugs.

Along with the rapid development of computer technology,numerical simulation has become a powerful tool to study the complex fluid dynamics of droplet-based micro fluidics over the last few decades[21-25].Among various numerical methods,volume of fluid(VOF)model has been widely employed to simulate the generation and breakup of droplets in microchannels due to the simple but accurate way for dealing with topological changes of the interface in the calculation of three-dimensional flows[26,27].Sang and co-workers[26]developed a numerical(VOF)and an analytical model to study the viscosity effect of the continuous phase on drop formation in a T junction in 2008.The prediction of drop sizes by using the analytical method shows a satisfactory agreement to the numerical result.In 2011,Bedram and Moosavi[28]successfully employed VOF model to investigate the breakup of mother drops to generate unequal daughter droplets in an asymmetric T junction with arms of different cross-sections.The numerical results were verified by comparing with an analytical theory in the limit of thin- film approximation.

Up to now,the asymmetric breakup of a droplet has not been studied systematically,especially the deep understanding of physical mechanisms.Recently,Wang and Yu[29]proposed a power law model to predict the volume ratio of the two unequal daughter droplets.Thus,based on their works,the volume of fluid(VOF)model in the commercial software FLUENT is used to investigate the asymmetric breakup of a droplet suspended in an asymmetric and axisymmetric flow field generated in a 3-dimensional(3D)cross-like micro-device in this paper.The asymmetry of the flow system is produced by putting the droplet at a position deviating from the balance point or by controlling the volume flow rate of the left and right exits.

2.Mathematical Formulations

2.1.Numerical model

The governing equations that include the equation of continuity,the equation of motion and the volume fraction equation for two-phase flows are written as follow:

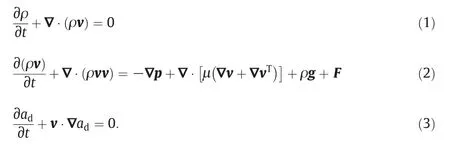
In these equations,ρ is the volume averaged density defined by Eq.(4),v is the velocity,μ is the volume averaged viscosity defined by Eq.(5),and Fis the continuum surface force(CSF)[30]which is adopted to include the surface tension in the momentum equation and defined by Eq.(6).

w here ρdand ρcare densities of the dispersed and continuous phase,adis the volume fraction of the dispersed phase,μdand μcare viscosity of the dispersed and continuous phase,σ is the interfacial tension and kdis curvature calculated from the divergence of the unit surface normal(Eq.(7)).

A transient,three-dimensional multiphase model in the commercial software FLUENT is employed.The PISO(Pressure-Implicit with Splitting of Operations)algorithm is used for pressure-velocity coupling.Spatial discretization terms were set as follow s:the PRESTO!method for the pressure term,second order upwind for the momentum equation,and the Geo-Reconstruction scheme for the volume fraction.

2.2.Validation of the numerical method

The numerical model is first verified for New tonian fluids by comparing the predicted results about the deformation of an initially spherical droplet in an axisymmetric extensional flow to those obtained by Stone and Leal[31].

The axisymmetric extensional flow is de fined by

w here the capillary number Ca=Gaμc/σ.G is the shear rate,a is the radius of the initially droplet,and σ is the stress tensor.Deformation parameter D=(L-S)/(L+S)is employed to describe the deformation of a droplet,w here L and S are the half-length and half width of the droplet,respectively.In addition,viscosity ratio:λ=μd/μc,was defined.

As shown in Fig.1,the predicted results(circles and stars)are very consistent to those obtained by Stone and Leal[31]for both λ=1 and λ=0.1,which verified the validity of the numerical model.

Fig.1.Drop deformation in a steady axisymmetric extensional flow:D versus Ca.The open circle symbols and solid line represent our results through VOF method and those of Stone[31]for viscosity ratio λ=1,respectively.The stars and dashed line represent our results through VOF method and those of Stone for viscosity ratio λ=0.1,respectively.

2.3.Parameters setup

In order to generate an axisymmetric extensional flow and to investigate the asymmetric breakup of a droplet trapped near the stagnant point,the micro-device show n in Fig.2 is designed.As show n in Fig.2(b),the continuous phase is injected into the device through the gap of two parallel circle plates,and flows out through the left and right exits.Thus,near the center between two parallel plates,an axisymmetric extensional flow is generated and the droplet will be put at or near the stagnant point of the flow.Fig.2(a)show s the details of the geometry from the front view,in which the unit is μm.

In order to improve the mesh quality,w e drew the mesh through O-grid method in ICEM CFD.Fig.2(c)is the illustration of the mesh,in which hexahedral elements are employed.The grid size around the axis of the device from the left to the right exit is about 2 μm,w here the grid is densest.In order to testify the accuracy of the chosen grid,a finer grid with the interval size of 1μm has been employed to calculate the asymmetric breakup of a droplet.It is found that the difference of the results from the two different grids is less than 2%.

The droplet(oil)is initially located at the center or near the center of the device,and the continuous phase(CP,water)is injected into the device through the circular inlet between two parallel plates.The velocity pro file at the inlet is

w here G is the shear rate at the wall of inlet,and A is the half width of the inlet.The velocity pro file of the outlet is Poiseuille flow and is calculated based on the mass conservation

w here Umaxis the maximum velocity,and R is the radius of the circular outlet.For simplification,w e set the densities of the droplet and CP equal in order to neglect the influence of the buoyancy-driven velocity in a typical oil-water micro fluidic system[32].The surface tension is 1 m N·m-1.The droplet and CP are both New tonian fluids,w hose viscosities are 0.0005 and 0.001 Pa·s,respectively.

3.Numerical Results and Discussions

Asymmetric breakup of a droplet could be achieved due to the asymmetry of its surrounding flow fields or due to the unevenness of its interfacial properties such as non-uniform interface tensions caused by uneven distribution of surfactants.The symmetric flow is show n in Fig.3(a),based on which the asymmetry of flow fields could be generated by many ways such as the asymmetric geometry of the channels,the uneven adjustment of the pressuresat different exits,the asymmetric effect of external force fields like the magnetic field,and the control of the initial location of the droplet.In this paper,w e will focus on the asymmetric breakup of a droplet in asymmetric flow fields generated by the deviation of the initial location of the droplet from the balance point of the flow field(case I,Fig.3(b)),and by changing the ratio of the volume flow rates at two exits(case II,Fig.3(c)).

During the past decades,the symmetric breakup of a droplet has been studied extensively.In the published work,the droplet is located exactly at the balance point of the symmetric flow field.Deformation parameter(D)and capillary number have been widely used in order to characterize the rheology behaviors of the droplet due to the shear of external flow s[4,6].How ever,in the investigation of an asymmetric breakup,a new parameter which defines the asymmetry of the flow field,must be introduced.In this paper,AS,which is a general symbol to describe asymmetry of the flow system and could have many expressions according to various causes of the asymmetry origination,has been employed.For instance,the asymmetry parameter ASis proportional to the location deviation and can be expressed as location asymmetry AS=(l-s)/(l+s)=xcen/a for case I(Fig.3(b)),and proportional to the volume flow rates at two exits and can be expressed as flow rate asymmetry AS=(QR-QL)/(QR+QL)for case II(Fig.3(c)).QRand QLare the volume flow rates of the right and left outlets,respectively.xcenis the distance between the initial location of the droplet center and the center of the flow field.a is the radius of the initial spherical droplet.In order to describe more asymmetric situations,the definition of AScould be generalized to AS=(XB-XS)/(XB+XS),where X indicates the physical quantity w hose unevenness leads to the asymmetry of the flow field,the subscripts B and S stand for the bigger and smaller values of the quantity,respectively.The range of ASvaries from 0 to 1.When AS=0,it means the physical quantity is even and the flow system is symmetric.The extreme value 1 of ASmeans that XS=0 and the droplet could not be broken at all and will move out of the flow field from one side due to the huge asymmetry.Capillary number Ca is important for both symmetric and asymmetric rheology behaviors of a droplet,especially for the critical capillary number Cac.C acis the parameter to determine whether the droplet will break up or not.ASfor the symmetric case,its value is mainly dependent on the properties of the droplet such as the viscosity.How ever,for asymmetric case,it is severely influenced by the asymmetry of the flow system.

Fig.2.The geometry of the channel from the front view(a).Sketch for the 3D channel(b).Illustration of the mesh of the cross-like channel from the left and front view(c).

Fig.3.Illustrations of a droplet suspended in symmetric and asymmetric flow fields.SP is the stagnation point,O and O′is the center of the flow field and droplet,respectively.l and s are the distances of the longest and the shortest point from the center of the device,respectively.Q L and Q R are the volume flow rates at the left and right exits,respectively.

3.1.Effects of location deviations from the balance point

In this section,droplets will initially be placed along the axis direction at the distance of 1,2,4,6,8 and 10 μm from stagnation point of the flow field(center of the device),respectively.For each location deviation,the capillary number is varied over a broad range by changing the inlet flow rate so that the different deformations and breakups could be observed.

3.1.1.Droplet breakup regimes

As for the symmetric deformation and breakup of a droplet,w hen Ca＜Cac,the droplet will finally reach an equilibrium shape;w hen Ca＞Cac,the droplet will breakup into two equal daughter droplets.How ever,as for asymmetric case,hydrodynamic regimes are more complicated as shown in Figs.4 and 5.

The rheological behaviors of a droplet for various C a in the axisymmetric extensional flow with AS=0.3 are show n in Fig.4.When Ca is very small(Ca=0.158)and ASis fixed to 0.3,mother droplet can't breakup and will move out from one side of the cross-like device(Fig.4(a),NB).With the increase of the Ca(Ca=0.164),as the elongated tail of the mother droplet is too thin to retract,the mother droplet will split from the drop similar to end-pitching fragmentation.This phenomenon is called one-side breakup(Fig.4(b),OB)because all of the breakup droplet will move into the same side of the device.A special kind of breakup so-called retraction breakup(Fig.4(c),RB)is observed w hen Ca is increased a little continually(Ca=0.166).When Ca is increased to 0.180,the droplet will be extended continuously until it breaks into two daughter droplets moving in the opposite direction(Fig.4(d),DB),which is similar to the breakup process of the symmetric case.The difference between RB and DB is that the left end of the elongated droplet will retract a little during the process of the RB.

Fig.4.Four different hydrodynamic patterns.(a)NB(no breakup),(b)OB(one-sidebreakup),(c)RB(retraction breakup),(d)DB(direct breakup).A S=0.3,Ca=0.158,0.164,0.166,and 0.180,respectively.

Fig.5.Droplet breakup regimes as a function of capillary number Ca and A S(□:NB,○:OB,◇:RB and△:DB).The dash line and the solid curve are employed to distinguish the different regimes.The solid curve is the critical capillary number(Ca c)as a function of the asymmetry.The horizontal solid line at A S=0 shows the symmetric breakup of a droplet and the solid circle(●)is the critical capillary number in symmetric case.

The four regimes of the asymmetric breakup of a droplet as function of Ca and ASare show n in Fig.5,in there the radius of the initial droplet placed in the device is 20 μm.Different regimes are marked by different symbols.In this figure,for a fixed A s,the transitions from NB to OB,RB and DB are observed when Ca is increased gradually.When Ca is fixed,the process of the w hole transition from NB to OB,RB and DB occurs along with the decrease of the asymmetry.Thus,in the regime(NB zone marked by squares)with low Ca or high AS,the droplet is squeezed firstly near the balance point,then moves into the right arms of the device and relaxes there.In this process,the droplet could not be broken up due to the relatively strong surface tension or due to the quick movement of the droplet caused by the high asymmetry of the flow.Along with the increase of C a or the decrease of AS,the regime transits into the OB zone(marked by open circles)and the boundary is draw n by the dash line.In this regime,as the shear action of the flow becomes a little stronger or the time taken by the droplet moving into one side of the arms gets a bit longer,the tail of the droplet is cut down and becomes a very small daughter droplet which follow s the main droplet and moves out of the device from one side of the arms.From the above description,it could say,whether the droplet could be broken asymmetrically or not is the result of the competition between the cutting action of flow and the oriented displacement of the droplet due to the asymmetry.After the breakup,the small daughter droplet and the main droplet move forward together in the right side of two arms and finally merge into one because of the parabolic velocity pro file of Poiseuille flow.As show n in Fig.5,the width of this regime increases gradually along with the increment of the asymmetry.The third regime(RB zone marked by diamonds)is very narrow.It is also a special process in which a retraction occurs during the droplet breakup.Along with the increase of Ca or decrease of AS,the shear action gets a bit stronger and the displacement of the droplet gets correspondingly.The mother droplet is broken into two daughter droplets which finally move out of the device from two different sides of the arms.The way to differentiate RB from DB zone is that there is a small retraction at the left end of the elongated droplet during the process of RB.This zone is so thin that it could be treated as the starting point at which the direct breakup regime begins.DB occurs when the capillary number Ca is big enough or ASis very small.In this process,the mother droplet breaks up directly into two daughter droplets moving in the opposite direction.The droplet break up soc curring in this regime are mainly affected by the strong shear force of the extensional flows in the device.When AS=0,it is a symmetric flow system and the regime is simply divided into two zones,NB and DB,by the critical point Cac.Here,Cacis defined as the capillary number above which the droplet will breakup into two daughter droplets moving in the opposite direction and is depicted by the solid curve in Fig.5.The width of RB regime is very narrow,which means that RB is a critical phenomenon.As the ASdecreases,the value of the critical capillary number decreases.

3.1.2.The power law model

As the main purpose to break a droplet asymmetrically is to collect droplets with different volumes,the prediction of the volume ratio rS=VB/VSof daughter droplets will be focused on the regime of DB.As for the symmetric breakup,the droplet never moves.The value of Ca does not change rSwhich is always unit,but will change the time taken to break the droplet.The larger Ca is,the larger the cutting speed of the flow should be.While,the situation will be different for an asymmetric breakup as the droplet will shift due to the asymmetry in the direction perpendicular to that of the cutting.The translation speed should be proportional to AS,and the translation distance is proportional to the product of the speed and the time needed to break the droplet,i.e.,AS=(a/Ca).Thus,rSmust be inversely proportional to Ca,but proportional to AS.When C a is extremely large,the droplet will be broken instantly,which means that the droplet has no time to shift.Thus,rSof the final droplets should be very close to the initial volume ratio r0.As show n in Fig.3(b),SPs are the stagnation point and regarded as the initial cutting point.The solid line connecting two SPs divides the droplet sin to two parts.r0is the volume ratio of the right to the left part.Thus,three major factors,which are critical to the process of asymmetric breakups w hen the initial droplet size is fixed,are the capillary number Ca determining the cutting speed,the asymmetry ASof flow fields which causes translation of the droplet,and the initial volume ratio r0.

Based on above analyses,a formula to calculate rSas a function of Ca and ASis given

where e,α and β are parameters fitted from data of numerical calculations.Cacare 0.122,0.128 0.145,0.165,0.192 and 0.226 for different asymmetries,respectively,which are obtained from Fig.5.r0is a function of ASand could be calculated by

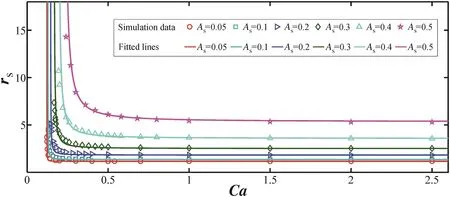
Fig.6.The volume ratios of two unequal daughter droplets versus Ca.

The data and their corresponding fitted lines[by Eqs.(11)and(12)]are show n in Fig.6.When Ca approaches Cac,rSwill go to infinity,and rSapproaches a constant along with the increment of Ca.This is consistent to our qualitative analysis in the first paragraph of this section.The fitted parameters e,α and β are 2.346,3.920,and 1.188,respectively.Substituting them into Eq.(11)and truncating Taylor expansion of r0to the term of third order,w e have an approximate equation

Eq.(13)could be employed to describe the breakup data with negligible errors when the asymmetry is small.

3.1.3.The effect of the droplet volume

In the previous section,the volume of the droplet was fixed.How ever,the effect of the droplet volume is also important in rheological behaviors of droplets.Thus,w e investigated the asymmetric breakup of droplets with different sizes including a=15,20,and 25 μm in this section.As the asymmetry AS=0.05 is fixed,the droplets are initially placed in this device with xcen=AS×.a=0.75,1,and 1.25 μm,respectively.The final results including the simulation data and their fitted lines are show n in Fig.7.As the initial volume ratio r0is only a function of the asymmetry AS,all these three curves eventually merge into one.The only difference for the three cases is the different critical capillary numbers.The bigger the droplet is,the smaller the critical capillary number is,which means that the larger droplet breaks more easily.The corresponding Cacare 0.124,0.122 and 0.109 for a=15,20,and 25 μm,respectively,which could be read from Fig.7.

3.2.Effects of the different volume flow rates at the two outlets

Besides the location deviation,the asymmetry can also be obtained by varying the volume flow rates at two exits.The difference of flow rates at exits will form an asymmetric flow field show n in Fig.3(c).The droplet is initially placed in the center of the device,i.e.the mass center of the droplet is the geometry center of the device.As shown in Fig.3(c),the connection line of the two stagnation points does not pass the mass center of the droplet,which causes the asymmetric breakup of the droplet in this part.

Compared to the asymmetric breakup of a droplet caused by location deviation,that caused by the different volume flow rates at two exits is much more complex.For instance,the streamlines become irregular near the center part of the device w hen AS=(QR-QL)/(QR+QL)is over 0.3 due to the constraint of the device w all.Thus,our analysis might not be appropriate w hen AS＞0.3.How ever,w hen ASis lower than 0.3,the streamlines are regular and the results show a quite good agreement to the power law model(Eq.(11)).

3.2.1.Droplet breakup regimes

Similar to those show n in Fig.4,four typical breakup hydrodynamic patterns also occur at different ASand Ca for this case.Fig.8 displays the four regimes of the droplet breakup and the transitions from one regime to another.The results are also similar to those show n in Fig.5.The width of the OB regime decreases with the decrease of AS.Also,the curve of the critical capillary number,across which the transitions from OB to RB and DB occur,decreases with the decrease of AS.When ASis equal to zero,the asymmetric flow field becomes the symmetric case,and the dash line and the solid curve converge into one point.This means that there are only NB and DB zones in the symmetric breakup of a droplet.Comparing Figs.8 to 5,the map for the case whose asymmetry is generated by two different volume flow rates at the two outlets(case II)has a wider OB zone than that for the case whose asymmetry is generated by location deviations from the balance point(case I).For case I,the flow rates at left and right exits are equal,and for case II,the flow rate at the right exit is larger than the left one.Thus,the flow rate at right exit for case II is larger than that for case I w hen the total flow rates are the same for both two cases.Furthermore,the stronger flow at the right side of device makes the one-side breakup occur at smaller Ca and makes DB occur at larger Ca.Therefore,case II has a wider OB zone.

Fig.7.The volume ratios of the two daughter droplets versus Ca at A S=0.05.

Fig.8.Droplet breakup regimes as a function of capillary number Ca and A S(□:NB,○:OB,◇:RB and△:DB).The dash line and the solid curve are employed to distinguish the different regimes.The solid curve is the critical capillary number(Ca c)as a function of the asymmetry.The horizontal solid line at A S=0 shows the symmetric breakup of a droplet and the solid circle(●)is the critical capillary number in symmetric case.

3.2.2.The influence of Ca and AS

Eq.(11)based on the power law could also be employed to predict the volume ratio of the two daughter droplets in this section.In order to calculate r0in Eq.(11),the asymmetry generated by the difference of the volume flow rates at exits should be converted to xcenin the location deviation case.After a careful analysis,the relation between the asymmetry employed in this section and xcenis given in Eq.(14)

Thus,the initial volume ratio r0could be calculated by combining Eqs.(12)and(14),

Fig.9 show s the data and the fitted lines[by Eqs.(11)and(15)]of rSas a function of Ca at AS=1/21(○),3/23(□),1/5(◇),7/27(△),and 9/29(☆),respectively.Cacare 0.121,0.133,0.145,0.156 and 0.167 for different asymmetries,respectively,which are obtained from Fig.8.These results show a quite good agreement between the data and the model.The fitted parameters e,α and β are 0.1794,1.505,and 1.098,respectively.Substituting the fitted parameters e,α and β into Eq.(11)and truncating Taylor expansion of r0in Eq.(15)to the terms of second order,we have

The approximate equation[Eq.(17)]could be employed to describe the breakup with negligible errors w hen the asymmetry is small.

As show n in Figs.6 and 9,rSdecreases rapidly and approaches the constant r0along with the increase of Ca.This means that the effect of Ca is only significant near the critical point.Beyond that,the volume ratio of the two unequal daughter droplets is only a function of the asymmetry AS.

4.Conclusions

By investigating the asymmetric breakup of a droplet in two different ways to generate asymmetries through a 3-dimensional VOF numerical model,it is observed that there are four typical regimes of the droplet rheological behaviors as a function of the capillary number Ca and the asymmetric parameter AS.There gimemap is plotted to describe the transition from no breakup(NB),to one-side breakup(OB),to retraction breakup(RB),and to direct breakup(DB).When the asymmetry of the flow system increases,the width of OB zone enlarges continuously.Also,the critical capillary number of the direct breakup increases along with the increase of the asymmetry.The effects of the capillary number and the asymmetry parameter are studied in details in the DB regime.Three major factors critical to the asymmetric breakups in DB regime,which are the capillary number Ca determining the cutting speed,the asymmetry ASof flow fields which causes translation of the droplet,and the initial volume ratio r0,are pointed out in this paper.Based on these qualitative analyses,a power law model is employed to predict the volume ratios of the tw o unequal daughter droplets for both two cases.The volume ratio rSis dependent on Ca

Fig.9.The volume ratios of two unequal daughter droplets versus Ca.

only in the region very near the critical capillary number.When Ca is large,rSis not a function of Ca,but only depends on the asymmetry

AS.As for the critical capillary numbers Cac,they vary with the different asymmetries and could be obtained in the droplet breakup regimes.When the radius of the initial spherical droplet is20μm,the critical capillary numbers are 0.122,0.128,0.145,0.165,0.192 and 0.226 for AS=0.05,0.1,0.2,0.3,0.4 and 0.5,respectively,in the flow system w hose asymmetry is generated by location deviations from the balance point(case I).Similarly,in the flow system w hose asymmetry is generated by two different volume flow rates at the two outlets(case II),the critical capillary numbers also increase along with the increment of AS,and are 0.121,0.133,0.145,0.156 and 0.167 for AS=1/21,3/23,1/5,7/27 and 9/29,respectively.In addition,it is found that the larger droplet has a smaller critical capillary number and breaks more easily.When the radii of the droplet are 15,20 and 25 μm,the corresponding Cacare 0.124,0.122 and 0.109,respectively,for case I and AS=0.05.Comparing the maps for case I and case II,the width of OB zone for case II is wider as the flow at the right side of the device is stronger in case II than that in case I.The information provided in this paper might be useful to understand the physics of droplet breakups and might be helpful in the design of droplet-based microfluidic devices.

Nomenclature

Subscripts

[1]M.Zerfa,B.W.Brooks,Prediction of vinyl chloride drop sizes in stabilised liquidliquid agitated dispersion,Chem.Eng.Sci.51(12)(1996)3223-3233.

[2]P.Wioletta,Modelling of high viscosity oil drop breakage process in intermittent turbulence,Chem.Eng.Sci.61(9)(2006)2986-2993.

[3]W.Podgórska,Influence of dispersed phase viscosity on drop coalescence in turbulent flow,Chem.Eng.Res.Des.85(5)(2007)721-729.

[4]G.I.Taylor,The formation of emulsions in definable fields of flow,Proc.R.Soc.Lond.A 146(858)(1934)501-523.

[5]B.Bentley,L.Leal,An experimental investigation of drop deformation and breakup in steady,two-dimensional linear flow s,J.Fluid Mech.167(1986)241-283.

[6]H.A.Stone,Dynamics of drop deformation and breakup in viscous fluids,Annu.Rev.Fluid Mech.26(1)(1994)65-102.

[7]V.Cristini,S.Guido,A.Alfani,J.Bławzdziewicz,M.Loewenberg,Drop breakup and fragment size distribution in shear flow,J.Rheol.47(2003)1283-1298.

[8]J.Janssen,A.Boon,W.Agterof,Influence of dynamic interfacial properties on droplet breakup in plane hyperbolic flow,AICHE J.43(6)(1997)1436-1447.

[9]D.Link,S.Anna,D.Weitz,H.Stone,Geometrically mediated breakup of drops in micro fluidic devices,Phys.Rev.Lett.92(5)(2004)054503-054506.

[10]T.Cubaud,Deformation and breakup of high-viscosity droplets with symmetric micro fluidic cross flows,Phys.Rev.E 80(2)(2009)026307-026310.

[11]Y.Navot,Critical behavior of drop breakup in axisymmetric viscous flow,Phys.Fluids 11(5)(1999)990-996.

[12]F.Rumscheidt,S.Mason,Break-up of stationary liquid threads,J.Colloid Sci.17(3)(1962)260-269.

[13]R.Fair,Digital micro fluidics:is a true lab-on-a-chip possible?Micro fluid.Nano fluid.3(3)(2007)245-281.

[14]S.-Y.Teh,R.Lin,L.-H.Hung,A.P.Lee,Droplet micro fluidics,Lab Chip 8(2)(2008)198-220.

[15]J.-T.Wang,J.Wang,J.-J.Han,Fabrication of advanced particles and particle-based materials assisted by droplet based micro fluidics,Small 7(13)(2011)1728-1754.

[16]L.Ménétrier-Deremble,P.Tabeling,Droplet breakup in micro fluidic junctions of arbitrary angles,Phys.Rev.E 74(3)(2006)035303-035306.

[17]M.Samie,A.Salari,M.B.Sha fii,Breakup of microdroplets in asymmetric T junctions,Phys.Rev.E 87(5)(2013)053003-053010.

[18]C.Chung,M.Lee,K.Char,K.H.Ahn,S.J.Lee,Droplet dynamics passing through obstructions in con fined microchannel flow,Micro fluid.Nano fluid.9(6)(2010)1151-1163.

[19]S.Protière,M.Z.Bazant,D.A.Weitz,H.A.Stone,Droplet breakup in flow past an obstacle:a capillary instability due to permeability variations,Europhys.Lett.92(5)(2010)54002-54007.

[20]L.Salkin,A.Schmit,L.Courbin,P.Panizza,Passive breakups of isolated drops and one-dimensional assemblies of drops in micro fluidic geometries:experiments and models,Lab Chip 13(15)(2013)3022-3032.

[21]J.Liu,N.-T.Nguyen,Numerical simulation of droplet-based micro fluidics,Micro Nanosystes 2(3)(2010)1-8.

[22]M.Wörner,Numerical modeling of multiphase flow s in micro fluidics and micro process engineering:A review of methods and applications,Micro fluid.Nano fluid.12(6)(2012)841-886.

[23]J.Wang,J.Liu,J.Han,J.Guan,Effects of complex internal structures on rheology of multiple emulsions particles in 2D from a boundary integral method,Phys.Rev.Lett.110(6)(2013)066001-066005.

[24]J.Tao,X.Song,J.Liu,J.Wang,Micro fluidic rheology of the multiple-emulsion globule transiting in a contraction tube through a boundary element method,Chem.Eng.Sci.97(2013)328-336.

[25]J.Wang,J.Liu,J.Han,J.Guan,Rheology investigation of the globule of multiple emulsions with complex internal structures through a boundary element method,Chem.Eng.Sci.96(2013)87-97.

[26]L.Sang,Y.Hong,F.Wang,Investigation of viscosity effect on droplet formation in T-shaped microchannels by numerical and analytical methods,Micro fluid.Nano fluid.6(5)(2008)621-635.

[27]S.Afkhami,A.M.Leshansky,Y.Renardy,Numerical investigation of elongated drops in a micro fluidic T-junction,Phys.Fluids 23(2)(2011)022002-022015.

[28]A.Bedram,A.Moosavi,Droplet breakup in an asymmetric micro fluidic T junction,Eur.Phys.J.E 34(8)(2011)34-45.

[29]J.Wang,D.Yu,Asymmetry of flow fields and asymmetric breakup of a droplet,Micro fluid.Nano fluid.18(2015)709-715.

[30]J.U.Brackbill,D.B.Kothe,C.Zemach,A continuum method for modeling surface tension,J.Comput.Phys.100(1992)335-354.

[31]H.A.Stone,L.G.Leal,Relaxation and breakup of an initially extended drop in an otherwise quiescent fluid,J.Fluid Mech.198(1989)399-427.

[32]M.De Menech,P.Garstecki,F.Jousse,H.Stone,Transition from squeezing to drip ping in a micro fluidic T-shap ed junction,J.Fluid Mech.595(2008)141-161.