基于1-bit压缩采样的快速频谱检测方法

［吴迪 李智］

基于1-bit压缩采样的快速频谱检测方法

［吴迪 李智］

摘要为解决已知的认知无线电感知算法对硬件依赖过高，或者实时性不好的问题，提出了将时下热门的1-bit压缩采样方法引入到频谱检测中，该方法通过对采样值进行极限量化，在融合中心恢复频点位置而不是幅度信息来实现频谱感知，极大地简化硬件结构，提高信号存储和传输速率。经数值仿真实验显示，在对信号进行1-bit量化以后，系统能在较短时间检测出频谱占用情况，大大提高了检测对实时系统的要求。新方案与基于传统的压缩感知（CS）算法相比，能获得远小于后者的检测时耗，同时获得更好的噪声鲁棒性。

关键词：认知无线电 1-bit压缩采样 快速检测

吴迪

硕士研究生，四川大学电子信息学院，主要研究方向：物联网与压缩感知技术。

李智

四川大学电子信息学院副教授，主要研究方向：压缩感知。

引言

当今，随着通信技术的快速发展，频谱资源越来越稀缺，这就需要我们对有限的频谱资源进行有效利用。高效的频谱感知技术需达到如下两点：第一，判断某一频段是否空闲可用；第二，为不对主用户（Primary User，PU）造成不良影响，次级用户（Secondary User，SU）在接入后要持续监听，达到在第一时间感知到主用户接入并让出信道。频谱感知需要对信号及时处理，一般要求能达到在毫秒间完成感知。已有的 CR 频谱感知技术可分为发射源检测(非协作检测)、协作检测和干扰温度检测等三大类。这里主要介绍发射源检测方法，我们综合这些算法的特性、性能优缺点，如表1。

表1　四种常见发射源检测算法性能优缺点比较

但是，随着带宽的逐渐展宽，这些技术都有一个共同的理论约束——奈奎斯特采样定理：在模数转换过程中若采样频率不小于信号中最高频率的两倍，则采样信号能完整保留原始信息。对高达GHz的宽带信号进行采样，超高的采样速率及庞大数据传输量将会对现有A/D转换器，DSP芯片处理带来极大挑战。这促使人们转而寻找能够实现低速率采样的新技术。压缩感知(Compressed Sensing, CS)正是在这种条件下应运而生，它打破了奈奎斯特采样定理的限制，利用了稀疏信号的自相关特性，仅通过少量检测点数便能实现信号的重建与检测，大幅降低系统对硬件的要求，极大推动频谱感知技术的发展与应用。因此，压缩感知技术成为了解决频谱感知的一个热门手段。

然而，在传统压缩感知中，测量值被当作实值，没有考虑量化，即有无限比特量化精度。在实际应用中，测量值必须量化到有限精度，为了进一步处理和储存，每个测量值被映射到有限比特范围。最近几年，陆续有学者展开了对量化的压缩感知理论的研究[1]-[4]，Boufounos和Baraniuk提出了一种极限量化思想[2]，通过一个比较器，与一个门限值进行比较，产生±1的测量值，即只保留信号的符号信息，只需少量测量值就能准确的恢复信号支撑集（在频谱感知中表示的就是频点的位置），如果增加测量值，还可以完美的恢复信号。在实际应用中，它有如下几个方面的优势：

（1）量化器是一个比较器，能够以较低的功率和较高的速率进行采样量化；

（2）1-bit量化对多种形式的噪声和非线性失真是鲁棒的；

（3）在确定条件下，1-bit压缩感知性能优于传统的多bit压缩感知。

这些优势说明了1-bit压缩采样比传统的感知算法和经典的压缩感知算法更适合做频谱感知。接下来第一节和第二节说明压缩感知模型和优秀的1-bit重构算法，第三节是数值仿真，最后一节是结束语。

1　1-bit压缩采样模型

1.1传统压缩感知模型

压缩感知模型信号的稀疏性是压缩感知理论应用的前提。假设实值离散时间信号X∈RN是N×1维列向量。其中RN空间的任何信号都可以用N×N维的规范正交基向量的线性组合表示。则X在一组正交基下进行展开成式（1）

我们知道，在压缩感知理论中，可压缩信号X∈ RN经过投影矩阵Φ的观测之后，如果其满足约束等距性条件(Restricted Isometry Property，RIP)则可以仅由M= O( K lg( N / K ))=N个线性观测值恢复出来，观测方程为式（3）

其中Φ为M×N(M N)维投影矩阵。利用M维观测值Y恢复信号X的过程称为信号重构，重构模型可写为式（4）:

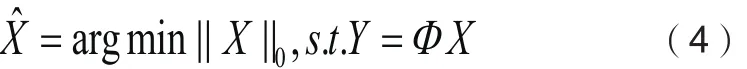
其中求解式第一个式子是L0范数最小化求解问题，是非凸的，无法直接求解。从压缩感知算法提出至今，学者们提出了很多不同的解法，其中贪婪迭代算法因算法结构简单、运算量小而颇受关注，应用比较广泛的算法有匹配追踪(MatchingPursuit, MP)、正交匹配追踪 (Orthogonal Matching Pursuit，OMP)及子空间追踪(Subspace Pursuit, SP)等。

1.21-Bit压缩感知模型

在现实环境中，观测值y必须经过量化处理后，才能进行数字处理，进而恢复信号。量化模型可写为式（5）：

其中QB表示B-bit量化，即将通过压缩采样每一个采样值量化到Bbit。当 B 取值为 1 时，表示1-Bit量化。1-bit量化是对观测值进行量化处理的一种极限情况，即仅保留观测值的符号信息。通常情况下，量化过程电压比较器的比较电压取为零[2]，则1-bit压缩感知量化模型可写为式（6）：

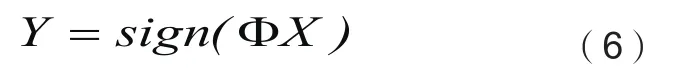
其中，sign(.)为符号函数，只取±1。观测值向量Y可构成M×M的对角矩阵Y= di ag( Y )。根据符号一致性原理，可得YΦ X≥0。由于1-Bit压缩感知仅保留观测值的符号，信号的幅度信息丢失，重构模型用L1范数作为衡量信号稀疏性标准。为了确保得到非零解，并克服幅度不确定性问题，在单位L2球面，如式（7）

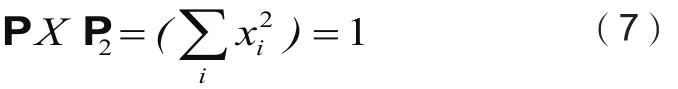
上重构信号。 1-Bit 压缩感知重构模型为式（8）

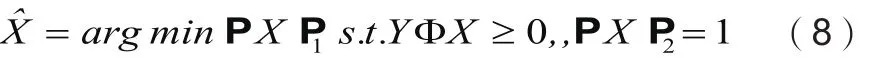
式中，最小L1确保得到稀疏解，第一个约束条件增强观测值与解之间的一致性，第二个约束确保得到有效解。解的准确性依赖于观测值的Bit位数。

2　1-Bit压缩采样重构算法

2.11-bit应用于快速频谱检测的可行性

在频谱感知网络中，感知节点把对宽带频谱的感知信息发送给融合节点，对于动态变化的频谱来说，当感知网络中包含较多感知节点时，感知节点向融合节点频繁的传送更新信息将极大地消耗感知网络中的通信带宽，甚至可能导致网络无法运转。如果能对感知信息进行有效的量化，简化传送的信息，那么网络带宽压力将得到缓解。1-bit 压缩感知能对压缩感知采样得到的数据进行 1-bit 量化，得到一系列值为±1 的数据，将采样和量化过程结合在一起，大大简化了前端硬件压力和带宽压力。每次频谱感知之后，各感知节点只需把量化后的符号信息发送给融合节点，那么将使融合节点中信号的接收设备得到简化，发送数据可采用信道编码理论对其进行纠错编码，确保融合节点接收到高质量的可靠信息。由1-bit压缩理论可知，1-bit 量化之后重构的原始信号是在单位能量约束下的信号，在频谱感知中只需判断某个频段是否存在主用户进行通信，无需对信道的能量信息进行判决，因此只需得到信号在频域的稀疏解，无需对信号进行精确重构，这表明 1-bit 量化对于频谱感知系统是适用的。

2.21-Bit感知算法

1-Bit 压缩感知的重构算法可分为两大类：凸算法与非凸贪心算法。文献[2]在固定点连续(Fixed PointContinuation, FPC)算法的基础上，增加梯度投影和球面约束思想，提出 BFPC(Binary FPC)算法，该算法为凸正则化算法。匹配符号追踪算法(Matching Sign Puisuit，MSP)[11]是在CoSaMP算法的基础上提出的一种贪心算法。文献[9]介绍了类似于非凸优化中的信赖域算法——限制步长收敛算法(Restricted Step Shrinkage, RSS)，该算法具有较好的收敛性，计算速度快，重构信噪比较高。文献[7]提出二进制迭代硬阈值算法(Binary Iterative Hard Thresholding，BIHT)，文献[8]提出一种快速精确的两级 (Fast and Accurate Two-Stage,FATS)信号重构算法，在上述算法中最突出的算法是BIHT 算法，该算法较其它重构算法的重够效果更好，表现为较高的重构信噪比和一致性，且计算过程简单，复杂度低。

BIHT算法最初是在迭代硬阈值(Iterative HardThresholding，IHT)算法[10]的基础上改进的。IHT算法是处理压缩感知问题的一种常用算法，该算法是求解满足约束条件的优化问题，IHT算法十分简洁，采用迭代式（9）：

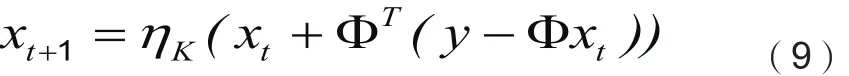
其中xt为第 t 次迭代值，ηK( β )是一个非线性算子，它将矢量β中幅度最大的前K个元素以外的所有元素设置为零。IHT 算法的迭代式(8)可分解为两步：

BIHT算法结合了1-Bit压缩感知特点，用最小一致目标代替IHT算法的第一步，其算法步骤如下：

（1）初始化：x0=， 0残差的初始值r0= y；

（3）硬阈值投影xt= ηK(βt)，其中为非线性算子，保留βt的前L个最大元素，其余元素置零，计算残差rt−1= y− si gn(Φxt)；

（4）若rt−1中非零元素个数为零，或者t=maxiter，迭代停止。否则t=t+1;

3　实验结果及分析

本文假设，SU需要对频谱宽度为[0,50MHz]的频谱信号进行感知，频带被划分为25个信道，则每个信道带宽为2MHz,信道之间彼此互不重叠，其中活跃信道数为5，信号维度N=256，采用1-bit压缩采样维度为M=200为检测1-bit重构算法的抗噪性，在传输过程中加入随机高斯白噪声，传输信噪比为7dB,单次实验结果如下：

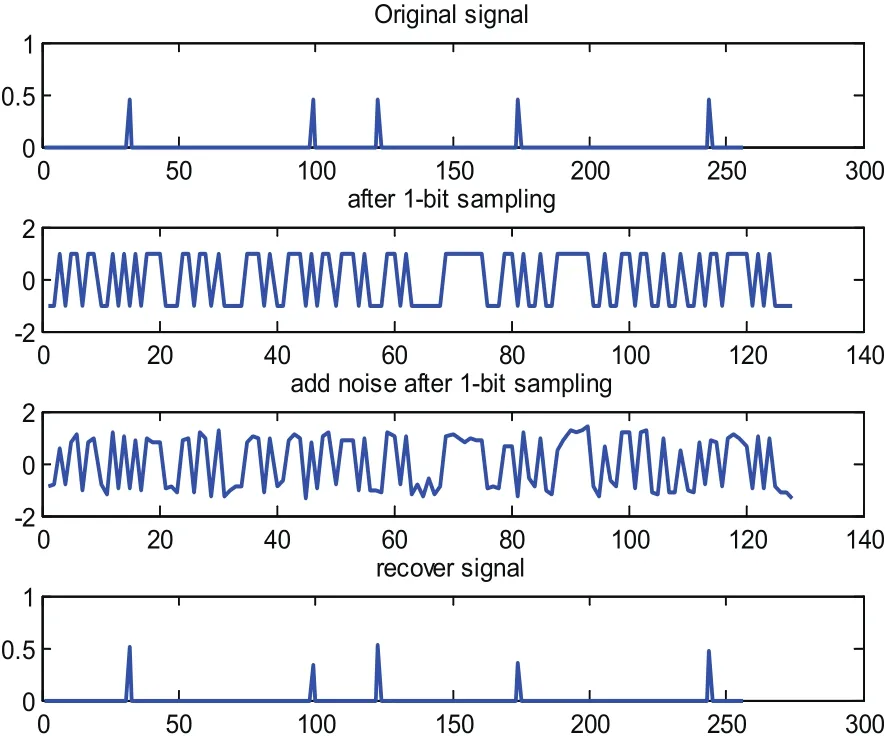
图1　频点位置随机的信号传输过程中加入7dB噪声后的重构信号

从图1可以看出，当取采样点数M=128,仅为奈奎斯特采样点数N的一半，且在1-bit量化后加入噪声后，虽然恢复信号幅度有所改变，但算法仍然能够准确感知信号频点的位置，充分证明了1-bit压缩采样重构算法在频谱感知中的可行性。为了证明算法的有效性和稳定性，我们以频谱感知中的检测概率Pd作为衡量标准，通过不通信噪比下，该算法的检测概率，设定每种信噪比下检测次数T=1000,其中检测概率的定义如式（10）：

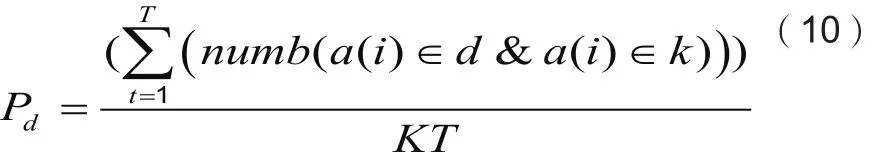
其中K表示活跃信道数，分子表示随机活跃信道数与估计活跃信道数的交集。

这里以经典的压缩感知算法—OMP（Orthogonal Matching Pursuit，正交匹配追踪）算法作为比较对象，采用8-bit量化，采样维度为M2=50,则总传输数据量为tol2=400bits，1-bit压缩采样重构算法采样维度为M1=200，总的传输值为tol1=200bits。经MATLAB仿真，实验结果如图2：

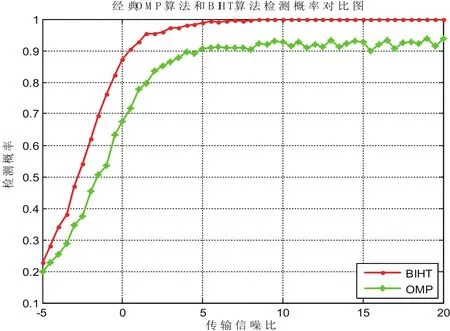
图2　经典OMP算法和1-bit重构算法算法检测概率比较

由图2可知，当信噪比为0dB时，即噪声强度与信号强度相当的情况下，BIHT算法检测概率为80.5%，而OMP算法的检测概率为68.3%。当信噪比为8dB时，1-bit算法正确检测概率高达95.5%，而总的数据传输量仅相当于传统压缩感知算法的一半，大大的降低了传输时间和效率，是一种有效的频谱感知方法。在需要传输大量数据的网络中，这种优势将更为明显。

4　结束语

本文介绍了认知无线电网络常用的感知方法，这些方法有其优点，但是在当今频谱资源越来越稀缺，带宽需求不断扩展的情况下，1-bit压缩采样有着无可比拟的优势，在采样端用比较器代替高速ADC转换器，极大地降低了硬件压力，适合低功耗的场景。传输端减少了数据传输量，极大地缓解了带宽压力，随着技术发展的成熟，相信在不久的将来，我们将体验到其带来的便利。

参考文献

1Laska J N, Boufounos P T, Davenport M. A, et al. Democracy in action: Quantization, saturation compressive sensing[J]. Applied and Computational Harmonic Analysis,2011, 31(3): 429-443

2Boufounos P and Baraniuk R. 1-Bit compressive sensing[J]. Sciences and Systems, 2008: 16-21

3Donoho D L. Compressed sensing[J]. IEEE Transactions onInformation Theory, 2006, 52(4): 1289-1306

4张京超,付宁,杨柳. 1-Bit压缩感知盲重构算法[J]. 电子与信息学报,2015,03:567-573

5Boufounos P. Greedy sparse signal reconstruction from signmeasurements[C].Prceedings of the Asilomar Conference onSignals Systes and Computers, Asilomar, California, 2009:1305-1309

6Laska J, Wen Z W, Yin W, et al.. Trust, but verify: fast andaccurate signal recovery from 1-bit compressive measurements[J]. IEEE Transactions on Signal Processing,2011, 59(11): 5289-5301

7Jacquesy L, Laska J N, Boufounos P T, et al.. Robust 1-Bitcompressive sensing binary stable embeddings of sparsevectors[J]. IEEE Transactions on Information Theory, 2013,59(3): 2082-2102

8孙彪. 基于压缩感知的信号频谱测量方法研究[D]. [博士论文],华中科技大学, 2013

9Plan Y and Vershynin R. One-bit compressed sensing bylinear programming[J]. Communication on Pure and AppliedMathematics, 2013, 66(8): 1275-1297

10Blumensath T and Davies M. Iterative hard thresholding forcompressed sensing[J]. Applied Computational HarmonicsAnalysis, 2009, 27(3): 265-274

收稿日期：（2015-12-11）