一种加性色噪声下的DOA估计新算法

［汪弟杰　王敏］

一种加性色噪声下的DOA估计新算法

［汪弟杰王敏］

摘要针对现有的高分辨的DOA估计算法在加性色噪声下会失效的情况，文章提出了一种加性色噪声下DOA估计的方法。通过对接收数据的相关矩阵进行预处理，减小了加性色噪声对DOA估计的影响。利用一种新的求根算法代替特征分解，增加了准确度，减小了计算量。计算机的仿真结果证实了算法的有效性。

关键词：加性色噪声 空间非平稳噪声 DOA估计 相关矩阵 求根算法

汪弟杰

女，重庆邮电大学研究生，研究方向为加性色噪声下的DOA估计。

王敏

重庆邮电大学重庆市移动通信技术重点实验室。

引言

空间波达方向估计是空间谱估计研究的一个重要研究方向，目前的研究中，大多数算法都只在天线阵元噪声为高斯白噪声的理想场景下有效，然而，实际生活环境中却很难达到这一理想情况，因此色噪声情况下的阵列信号处理研究已经成为了研究的热点[3-10]。

在实际应用中，各个阵元之间噪声不相关，噪声只对阵列数据相关矩阵主对角线上的项有贡献，但各个阵元噪声功率不相等，且各通道的噪声特性也难以完全一致。对于这种空间空间非平稳噪声的情况，文献[3]提出了改进的幂迭代算法的差分平滑方法，但其估计精度依赖于变换矩阵参数的影响；文献[7]将噪声协方差矩阵模拟为已知权矩阵的参数化线性组合，再利用极大似然方法联合估计参数和信号方向，但这需要高维搜索，计算复杂；文献[5]在利用广义协方差差分方法排除掉平稳噪声信息后，根据斜投影算子的性质排除独立信源，对剩余的相干信源则可采用修正空间平滑算法恢复为满秩，进而用传统MUSIC算法进行DOA估计,但是计算较为复杂；文献[4]通过利用估计的噪声相关矩阵对接受数据相关矩阵进行预处理，消除了空间非平稳噪声方位估计的影响，本文在文献[4]的基础上，将改进的求根MUSIC算法引用到了算法中，从而减小了计算量，提高了信号估计的准确度，计算机仿真结果验证了扩展的有效性。

1　信号模型

本文考虑远场信号情况，M个传感器阵元阵接收L个信源，阵元间距为d，入射波长为λ，信源方向分别为θ1,…,θn，阵列信号矢量可以表示为：

其中，X(t)为接收机接收到的信号，A(θ)为接收信号的方向矩阵，S(t)为接收信号的复包络矢量，N(t)为噪声矢量，且方向矩阵其中为信号矢量，为第i个窄波的振幅，且噪声矢量为N(t)=[N1(t)N2(t)…NM(t)]T。

由式（1）可得协方差矩阵为

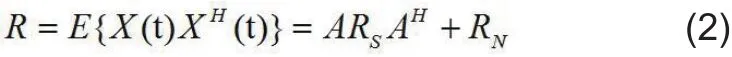
其中RS为信号相关矩阵,{}H表示共轭转置,由于假定接收L个信号源情况，RS为可逆矩阵，RN为噪声协方差矩阵，假定信源数目L已知，且M≥3L，由于阵元噪声为加性色噪声，先估计Q3，将R的行、列按[L, L, M-L]进行分块，得到如下式子：

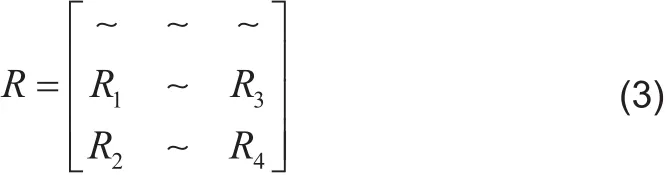
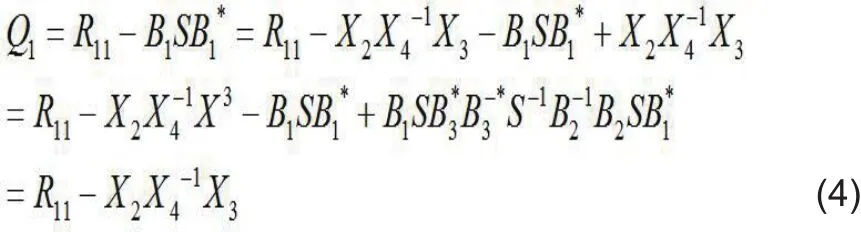
2　改进的求根MUSIC算法

求根MUSIC算法(Rooting-MUSIC)是改进的MUSIC算法多项式求根形式，是用多项式求根的方法来替代MUSIC算法中的谱搜索。其原理与MUSIC算法原理是一样的,只是需要用的矢量来代替导向矢量,从而用求根过程代替搜索过程,由于该式中存在的共轭项,修正得求根MUSIC 多项式

然后按照下式

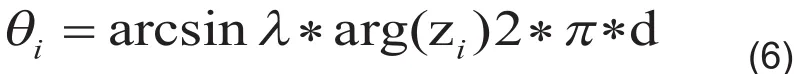
本文对求根MUSIC算法进行改进，由式（5）得

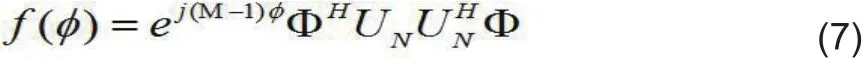
对式（6）进行求导，得

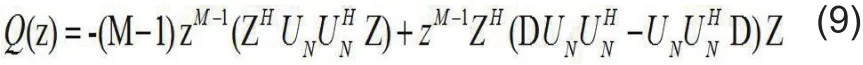
其中D=diag{0,1,2,K M-1}。

由于Q(Z)是2(M-1)次多项式，它的根相对于单位圆为镜像对。其中，取单位圆内具有最大幅值的K个根的相位给出DOA估计，可得信号源的DOA方向。

改进算法步骤：

（3）由公式（8）和公式（9）估计出信号的来波方向。

3　仿真分析

为了验证本文方法的有效性，作下面的仿真实验。实验中，假定M=10，L=2，阵元间距d=λ/2，且两个窄带空间不相干信号到达方向分别为10°、15°，背景噪声为空间非平稳噪声。快拍数为1024，实验结果取500次Monte Carlo实验的平均数据，信噪比定义为：其中输出噪声的功率噪声平均功率为4.87，为信号的功率，其中噪声功率是根据空间非平稳噪声情况下，噪声之间不相干，即噪声的协方差矩阵具有对角结构的特点来选取的，具有典型性。

图1是在SNR=[-4,-2,0,2,4,6,8]的情况下，文献[4]中算法和本文算法均方根误差随信噪比变化曲线的比较，其中虚线是文献[4]的数据，实线是本文改进算法的数据，从图中可以看出，随着信噪比的增加，两种算法的均方根误差都随着减小，但是本文算法的均方根误差值更小，所以可得本文算法的误差更小，性能更好。

图2是在SNR=0dB的场景下均方根误差随快拍数变化曲线的实验结果，其中虚线是文献[4]的数据，实线是本文改进算法的数据，从图中可以看出，随着快拍数的增加，两种算法的均方根误差都随着减小，但是本文算法的均方根误差值更小，所以可得本文算法的性能更好。

图3中，M=5，阵元间距为半个波长，远场窄波到达方向为2°，SNR=0dB，噪声相关矩阵为

图1　均方根误差随快拍数变化曲线

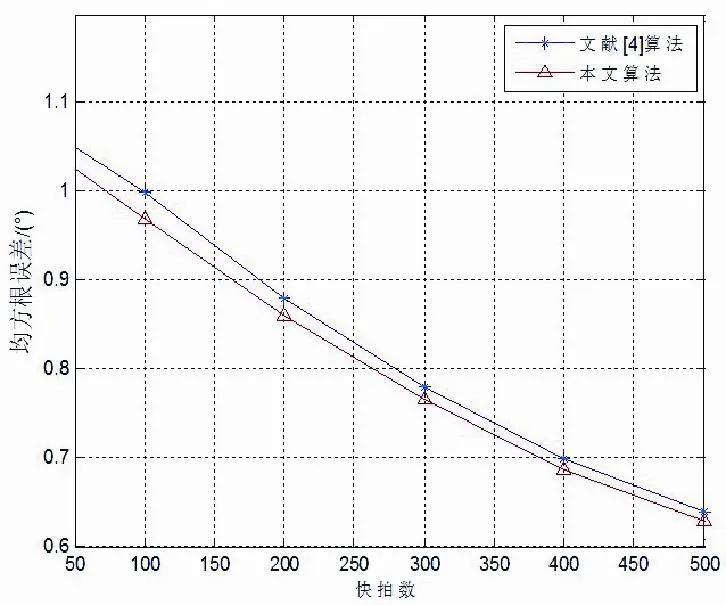
图2　均方根误差随快拍数变化曲线

图3　均方根误差随特征值数变化曲线

4　结束语

本文提出了一种加性色噪声下的DOA估计新算法，它可以有效的估计出加性色噪声的相关矩阵，并且通过利用改进的求根MUSIC算法减小了计算量，方法简单，性能稳健，且改进的求根算法不需要进行特征值分解，提高了计算速度和估计精度，具有很强的实用性。理论分析和仿真结果证明了算法的有效性。

参考文献

1张小飞, 汪飞, 陈伟华. 阵列信号处理的理论与应用[M]. 北京:国防工业学出版社, 2013: 71-83

2Gao F, Nallanathan A. Blind maximum likelihood CFO estimation for OFDM systems via polynomial rooting[J]. Signal Processing Letters, IEEE, 2006, 13(2): 73-76

3李哲, 张永顺, 王布宏. 非平稳噪声背景下相干信源DOA估计研究[J]. 现代防御技术, 2010,28(4): 132-136

4曾耀平, 刘毓. 空间非平稳噪声下的DOA快速估计新算法[J].数字信号处理, 2008,31(8): 68-71

5童宁宁, 郭艺夺, 门健. 非平稳噪声背景下多径信号的DOA估计方法[J]. 空军工程大学学报（自然科学版）, 2008,9(6): 38-41

6陈明建, 罗景青, 刘春生. 空间非平稳高斯噪声背景下混合信号的DOA估计[J]. Fire Control &Command Control, 2012, 37(1): 168-171

7Li M, Lu Y. Maximum likelihood DOA estimation in unknown colored noise fields[J]. Aerospace and Electronic Systems, IEEE Transactions on, 2008, 44(3): 1079-1090

8Werner K, Jansson M. On DOA estimation in unknown colored noise-fields using an imperfect estimate of the noise covariance[C]//Statistical Signal Processing, 2005 IEEE/SP 13th Workshop on. IEEE, 2005: 956-961

9Jianguo L, Bingcheng Y, Xing M. The CRB on wideband direction of arrival estimation under the background of colored noises[C]//Power Electronics and Intelligent Transportation System (PEITS), 2009 2nd International Conference on. IEEE, 2009, 1: 416-419

10Werner K, Jansson M. Efficient use of signal-free samples for DOA estimation and detection in colored noise[C]// Signal Processing and Information Technology, 2006 IEEE International Symposium on. IEEE, 2006: 666-671

11Chendeb M, Plantier G, Sourice A. Parameters and DOA estimation based on wavelet packets selection for transient signals in colored noise[C]//Signal Processing Conference, 2007 15th European, 2007,9(3-7): 2469-2473

收稿日期：（2015-11-03）