未来5G通信系统中低复杂度预编码算法研究
[董志明]
未来5G通信系统中低复杂度预编码算法研究
[董志明]
摘要作为未来5G通信系统关键技术技术之一的大规模MIMO技术能够明显的提高频谱利用率,预编码技术是MIMO系统的重要研究方向之一,因此得到广泛的研究。然而,在大规模MIMO系统中随着系统天线数量增加其预编码的计算复杂度非常大,因为其预编码计算包括多维矩阵的求逆,成为5G通信中大规模MIMO系统的应用一个难题。文章通过对RZF预编码中的矩阵进行改进,提出了一种复杂度相对较低的TPE预编码算法。仿真结果表明TPE算法相对RZF预编码计算复杂度有很大的改善,而且性能接近RZF预编码。
关键词:RZF预编码 系统容量 参数优化 多入多出
董志明
男,重庆邮电大学通信新技术及应用研究中心,信息与通信工程专业,硕士研究生,研究方向为无线通信系统MIMO算法研究。
1 引 言
现在的通信技术无法满足日益增长的数据传输速率需求,因此5G技术的发展将是不可避免的,大规模MIMO系统将成为5G通信系统的关键技术之一。传统MIMO系统基站天线数目往往少于10个,然而在大规模MIMO系统中基站有几十或几百以上的天线数目,大规模MIMO比传统MIMO获得更高的数据速率,因此得到广泛的研究。
在大规模MIMO系统中主要以线性预编码为主,因为非线性预编码复杂度高很难在大规模MIMO中应用。线性正规化迫零(RZF)预编码的计算复杂度相对较低,更适合大规模MIMO系统。由文献[3]知,当天线数目N和用户数K很大时,RZF预编码成为大规模MIMO系统中最优预编码方案。然而RZF预编码计算时需要求矩阵的逆,所以其计算复杂度相对较高很难实际应用。本文介绍了一种大规模MIMO下行链路系统中低复杂度预编码算法并进行参数优化以及仿真分析。
2 系统模型和问题分析

图1 下行链路系统模型
本文采用大规模MIMO单小区下行链路作为系统模型,基站有M根天线,服务K个单个天线的用户终端,K 和M都很大,而且比率β=K/ M 是常数;信道矩阵G= Q1/2H包含实对角阵Q的平方根,Q表示路径损耗,随机复数阵G代表慢衰落代表预编码矩阵,X∈{ RZF, TPE},分别代表TPE和RZF预编码,d=[d1... dK]T表示发射信号。
接收信号的叠加后的向量为:

其中y=[y1,... yk]T,yk表示第k用户接收到的符号,n=[n,..., n]T~CN(0,σ2I )表示复高斯白噪声向1k nK量,其元素均值为零,方差为
RZF预编码矩阵表示为:
其中ρ表是正则化因子参数,归一化因子ζRZF需要满足一下能量约束公式:
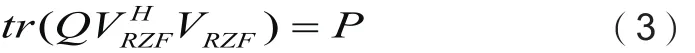
在(3)式中P表示总传输功率,可以利用文献[4]中矩阵处理算法对RZF预编码矩阵VRZF进行矩阵多项式扩展得到RZF预编码的近似逆矩阵,进而推导出TPE预编码算法表示为:

在(4)式中ωl, l∈{0,..., L }是矩阵多项式参数,ζTPE和(2)式一样是归一化因子满足:
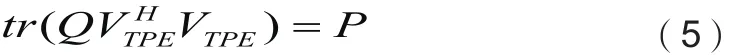
当K, N→∞时,系数ωl并不依赖于信道状态信息(CSI)的瞬时值,可以利用随机矩阵的相关理论计算出来并可以优化。
3 复杂度分析
在本节中,我们通过理论比较RZF和TPE预编码的复杂度。复杂度的计算等价于对于给定的四则运算进行加法和乘法运算的运算次数[10]。
在每个相干时间内RZF预编码矩阵总共需要进行四则运算操作次数为:
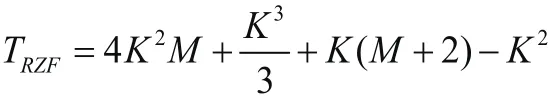
在每个相干时间内TPE预编码矩阵总共需要进行四则运算操作次数为:
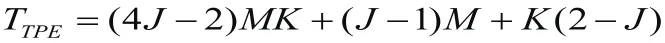
在大规模MIMO系统中,随着M、K的无限增大,RZF预编码算法的计算复杂度为o( K2M ),TPE预编码算法的计算复杂度为o( KM ),因此TPE预编码算法相对于RZF预编码算法计算复杂度降低很多。
4 TPE预编码算法优化
基于文献[7]中定理8,可以得到近似的功率限制表达式为:
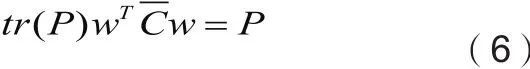
现在最大化用户k的近似SINR表达式:
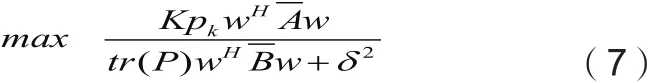
(7)式满足(6)式的功率限制关系。
设λmax是(8)表示矩阵的最大特征值,a是λmax对应的一个单位规范特征向量;
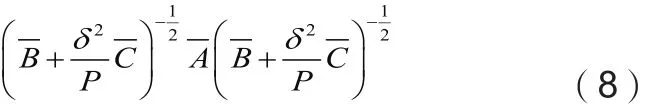
(8)式中的最优值为:
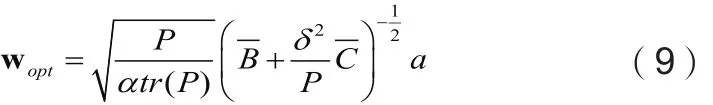
当w取最优值wopt时,用户k的SINR的近似值为:
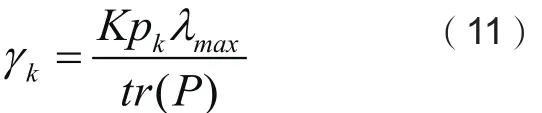
证明:利用wHCw= P,(7)式的问题就可以重写为:
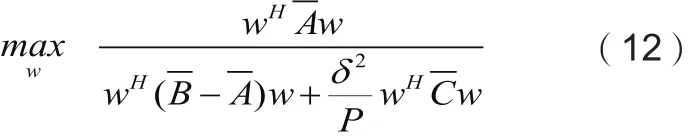
(12)式满足wHCw= P。

即(12)式的表达式可以等价表示为:
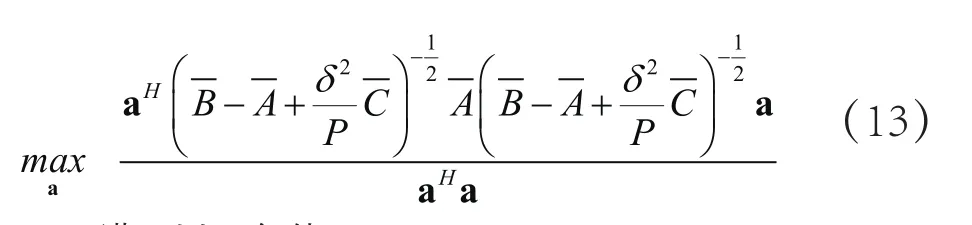
满足以下条件:

(13)式可以看成是关于向量a的函数,因此向量a的某个值可以使得(12)式取得最大值。不考虑常量参数,可以利用文献[9]中凸优化理论中典型的瑞利商最大化定理求解,当a是(13)式取得最大特征值时对应的特征向量,则(13)式可以取得最大值。

5 仿真分析
本部分通过模拟仿真,比较RZF和TPE预编码的性能。目的是为了验证所提出的预编码方案性能,以及说明一些主要的特性。本文采用的性能评定标准就是用户可以获得平均传输速率[11],如下式:
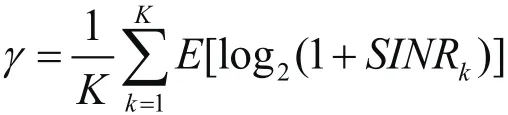
在大规模MIMO下行链路系统中,基站天线数目M=128,用户数目K=32,σ2=1,α=0.1,仿真结果如下:
仿真图2表明:当τ = 0.7,即当信道估计差时,RZF和TPE预编码几乎获得相同的用户传输速率;SNR较小时RZF和TPE预编码几乎获得相同的用户平均传输速率;但是当SNR较大时或者τ较小时,RZF和TPE预编码获得用户平均传输速率相差较大:
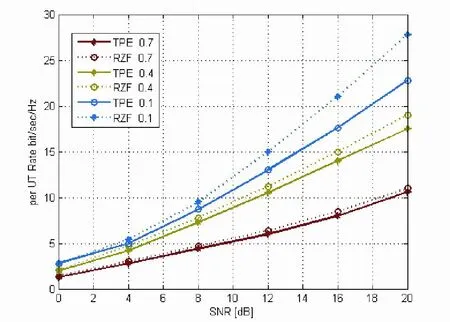
图2 不同信道估计下RZF和TPE算法
仿真图3表明:描述了用户获得的传输速率和TPE预编码参数J的关系。仿真表明当J越大时TPE预编码性能越接近RZF预编码性能。然而TPE的性能没有超过RZF的性能,但是TPE的J较小时就可以逼近RZF预编码的性能,即运用有限的矩阵多项式就可以接近RZF性能。
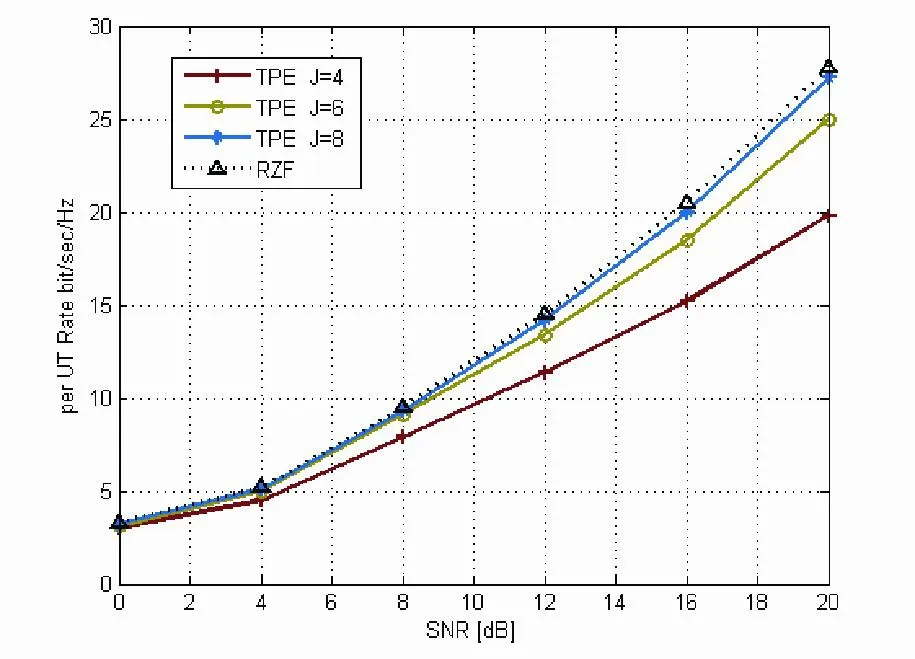
图3 不同展开项数J的性能比较
仿真图4表明:TPE预编码采用最优参数和完全已知信道状态信息下的性能仿真;低SNR时,三种情况的性能没有差距,但是当SNR较大时,三者性能有所差距但不是差距太大。经过参数优化的TPE预编码算法的性能更加接近RZF预编码算法。但是优化后的TPE预编码算法依然不能超过RZF预编码的性能,可以达到RZF预编码95%的性能,已经很接近RZF预编码算法的性能,满足性能要求,因此可以作为RZF预编码算法的替代算法在大规模MIMO系统中运用。

图4 TPE算法参数优化后性能比较
6 总结
在本文中,我们提出了一个在5G网络中大规模MIMO系统的下行传输中基于低复杂性矩阵多项式的预编码方案。仿真表明,TPE预编码矩阵取最优参数时,利用少数矩阵多项式项也可以逼近RZF 预编码的用户平均传输速率,提出的TPE预编码方案相对于RZF预编码器显著降低了计算复杂度,而且性能接近RZF预编码,因此本文所提预编码算法可以在5G通信大规模MIMO系统中作为RZF预编码的替代算法,来实现低复杂度预编码。
参考文献
1T. L. Marzetta. Noncooperative cellular wireless with unlimited numbers of base station antennas. IEEE Transactions on Wireless Communications, 2010, 11(6): 3590–3600
2H. Ngo, E. Larsson, T. Marzetta. Energy and spectral efficiency of very large multiuser MIMO systems. IEEE Transactions on Communications, 2013, 4(7): 1436–1449
3R.Zakhour,S.V.Hanly. Base station cooperation on the downlink: Large system analysis. IEEE Transactions on Information Theory, 2012, 4(2): 2079–2106
4F. Rusek, D. Persson, B. K. Lau, etc. Scaling up MIMO opportunities and challenges with very large arrays. IEEE Signal Processing Magazine, 2013, 1(6):40–60
5R. R. Müller, S. Verdu. Design and analysis of lowcomplexity interference mitigation on vector channels. IEEE Journal on Selected Areas in Communications, 2001, 8:
61429–1441
S.Zarei, W.Gerstacker, R. Müller, and R. Schober. Lowcomplexity linear precoding for downlink large-scale MIMO systems. IEEE International Symposium on Personal and Mobile Radio Communications (PIMRC), 2013,6(3): 1102-
71108
S. Wagner, R.Couillet, M. Debbah, etc. Large system analysis of linear precoding in correlated MISO broadcast channels under limited feedback. IEEE Transactions on
8Information Theory,2012,7(9): 4509–4537
R. Muharar and J. vans. Optimal power allocation for multiuser transmit beamforming via regularized Channel Inversion. inConference Record of the Forty Fifth Asilomar Conference on Signals Systems and Computers
9(ASILOMAR), 2011,5(3): 402-407
V.Nguyen and J.Evans. Multiuser transmit beamforming via regularized channel inversion, A large system analysis. IEEE Global Telecommunications Conference (GLOBECOM),
102008,7: 550-559
J.Evans and D.N.C.Tse. Large system performance of linear multiuser receivers in multipath fading channels. IEEE
11Transactions on Information Theory,2000, 6: 2059–2078
J.C.Bezdek and R.J.Hathaway. Convergence of alternating optimization. Neural, Parallel and Scientific Computations, 2003, 4: 351–368
DOI:10.3969/j.issn.1006-6403.2016.01.003

