不朽的名字属于纳什(NASH)

丁　利



不朽的名字属于纳什(NASH)

丁利

【摘要】约翰·纳什对博弈论的伟大贡献主要体现在以下四个方面：给出策略均衡的形式定义，并证明其存在性；对二人讨价还价问题进行公理刻画并得到纳什谈判解；提出探寻非合作博弈与合作博弈之间关系的纳什规划；最早提出关于博弈论理性与进化基础的两种解释。

【关键词】约翰·纳什策略均衡谈判解纳什规划博弈论基础

2015年5月23日，著名的博弈论大师和天才数学家约翰·纳什(John Nash)“刚从挪威领取阿贝尔奖(Abel Prize)，返抵美国后由机场乘出租车返家，谁料因此不幸遇难”。相比二十几岁早逝的伟大数学家阿贝尔，纳什的一生经历尤为曲折跌宕。但他与阿贝尔一样，“斯人已逝，英名不朽”。

博弈论作为关于“理性人的互动行为”的理论，已经发展成为分析理性决策者在策略互动局势下的行为选择模式的标准工具。可以说，博弈论在今天的社会科学体系中起着社会物理学的作用，成为几乎所有社会科学的语言。而纳什所提出的策略均衡解的概念和思想，是博弈论的核心与基础。他对博弈论的伟大贡献至少包括如下四个方面：给出纳什均衡的形式定义，并证明其存在性；对二人讨价还价(bargaining)问题进行公理刻画并得到纳什谈判解；提出探寻非合作博弈与合作博弈之间关系的纳什规划(Nash Program) ；开启关于博弈论基础的研究的大门，最早提出关于博弈论理性与进化基础的两种解释。

一、纳什均衡

在《20世纪数学的五大指导理论》(Five Golden Rules: Great Theories of 20th-Century Mathematics)中，卡斯蒂(John L. Casti)把冯·诺伊曼(John von Neumann)的最小最大定理列为其中的第一个，而在第一章的中间引入了作为其推广的纳什均衡存在性定理。这两个定理在博弈论发展史上起着里程碑式的作用，尤其是纳什的定理被视为博弈论的基本定理，这也是他1994年与豪尔绍尼(John Harsanyi)、泽尔腾(Reinhard Selten)同获诺贝尔经济学奖的主要原因。

一个博弈就是策略互动情形的描述(包括博弈者四个方面)：他们可选择的行动集合和行动的先后顺序，他们在博弈进行到不同阶段所掌握的信息及所持信念，他们的各种行动组合导致的结果以及每个人对结果的评价。而博弈的解就是对一类博弈能够如何进行并产生何种结果的刻画，包括每个参与人的行动方案(即行为策略)与信念系统，二者互相支持(静态情形下，一个人的策略同时也代表了对手关于他如何行动的信念)。

冯·诺伊曼1928年(恰巧就是纳什的出生年)关于二人零和博弈的“最小最大定理”(Minimax Theorem)是博弈论的第一个基础性贡献。该定理认为，如果两个人进行一项零和博弈(即常和博弈，你之所得为我之所失)，那么双方都存在一个可能是混合策略的行动方案，使得：你针对我的每一个策略选择恰当的应对从而产生我的一组最小支付，然后由我选择相应的对策而得到其中的最大值，这个值就等于：我针对你的每一个策略而选择恰当的应对而产生的一组最大支付，然后由你选择相应的对策而得到其中的最小值。用冯·诺伊曼自己的话说，如果没有最小最大定理，也许就没有博弈论。但是，对于范围更大的非零和博弈，这个定理并不成立。在冯·诺伊曼和摩根斯顿(Oskar Morgenstein)合著的巨作《博弈论与经济行为》(Theory of Games and Economic Behavior)中，对任何非零和博弈，通过引入虚拟的参与者——自然，把N人非零和博弈转化为N+1人的零和博弈，但这种变换的社会科学含义并不清晰，因而问题依然存在。这样纳什的工作就登堂入室了。

在普林斯顿大学的博士学位论文(其中，附录的大部分1951年发表于《数学年刊》中，纳什引入了以其名字命名的策略均衡并运用布劳威尔不动点定理(Brouwer Fixed-point Theorem)，证明其在任何有限博弈(参与者集合与每个参与者的行动集合都是有限的)中的存在性。纳什均衡的原始思想和概念可以追溯到法国经济学家古诺(Augustin Cournaut) 1838年对双寡头竞争的分析，但是纳什给出了一般情形下的定义。即，一个行动组合(严格来说是策略组合)在其他人不改变行动的情况下，每个人都没有激励单方面偏离而选择其他行动(定义中隐含地假设博弈者们独立选择行动，如果允许他们之间存在某种相关性，则可得到奥曼提出的相关均衡)。换句话说，所有参与人的行动策略互为最优的应对。爱好武侠小说的读者可以想象一下，两个武功高手以内力比拼的僵局，他们谁也不能撤回自己的掌力，这就形成一个纳什均衡。*这也提示我们，如果没有一个机制协调大家以形成集体行动或改变博弈的结构，所谓打破一个作为均衡的僵局，几乎难比登天。

纳什均衡的思想非常简单又美妙。几乎所有的博弈都涉及一个推理的循环。无论我选择一种什么行动，对手都会选择一种对付我的行动的最好招数，那么我就要选择一个对付他的对付我的行动的招数的最好行动，从而他就要选择一个对付我的对付他的对付我的行动的招数的行动的最好招数，如此以往。反过来，我选择一个行动，是因为我认为他会选择某个招数，而他选择这个招数是因为他相信我会选择某个行动，我选择某个行动是因为我认为他会选择某一个招数，也就是说“我认为他相信我认为他相信我认为他会选择某一个招数”，由此形成的信念阶梯可以无穷地进行下去。这个似乎解不开的哥尔丹之结(Gordian Knot)，就是豪尔绍尼当年也曾面对的“博弈者方面的相互预期的无穷回归”。而纳什均衡则是砍断此难结的亚历山大之剑。

如博弈论的经典之一《博弈和决策》(Games and Decisions)的作者卢斯(R. Duncan Luce)和莱法(Howard Raiffa)所指出的，“如果我们的非合作理论导致一个策略选择的组合，并且它具有这样的性质，即关于理论的知识不会导致一个人做出一个不同于理论预见到的选择，那么理论剥离出来的策略一定是均衡点”。Van Damme也指出，“博弈的解，作为一个建议集合，告诉每个博弈者在可能出现的场合如何行动。这样的解应该是协调的，没有博弈者有激励偏离他所得到的建议。由此，这个解是自我实施(self-enforcing)的……用博弈论的术语，解应该是纳什均衡”*Eric Van Damme. Stability and Perfection of Nash Equilibrium, Second and Enlarged Edition. Berlin Heidelberg: Springer-Verlag, 1991：2.。传统博弈论还提供了一些关于纳什均衡的直觉看法，典型的如“事前交流”(pre-play communication)、“自我实现的预言”(self-fulfilling prophecy)和“焦点”(focal point)解释。*George J. Mailath. Introduction: Symposium on Evolutionary Game Theory. Journal of Economic Theory, 1992, 57: 259—277.事前交流解释是说，如果博弈者事前讨论(或听一个博弈论学者给出建议)如何玩这个游戏，那么它一定是纳什均衡，要不就会至少有一个人有动力偏离这种玩法；自我实现的预言是指如果大家都知道一个理论预言游戏应该怎么玩，那它一定预言的是纳什均衡；焦点解释则认为，“如果一个博弈有一种明显的玩法(从博弈结构本身或它的设定得出)，那么博弈者们会知道其他博弈者正在干什么”。所谓均衡，就是大家都知道的明显的玩法。

当然，这并不意味着纳什均衡是博弈论的终结。实际上，与纳什同时获奖的豪尔绍尼就把它推广到处理信息不完全情形的贝叶斯博弈(Bayesian Game)；而泽尔腾则表明一个(动态)博弈中并不是所有的纳什均衡都有道理。博弈进行中参与人选择某个行为的可信性，就是我在某个特定局面下关于对手(过去或将来)会如何行动的信念，其中的过程特别复杂微妙，由此引发了均衡的精炼与筛选的研究蔚为大观。

我们也可以用一个囚徒困境(Prisoners’ Dilemma)博弈的翻版来说明纳什均衡。假想在一个法治不是特别健全的社会里，原被告打一场100万的官司，每个人都可以选择以30万金额贿赂法官或不贿赂(简单起见，我们假设只有这两种行动)。如果两个人都不贿赂，那么他会给出一个基本公正的裁定，原告60万，被告40万；但如果有一个人贿赂而对方没有，自然是没有贿赂的人倒了大霉，一分也拿不到；当然如果两个人都贿赂了法官，那么两下里扯平，他该怎么判就怎么判。(如图1)

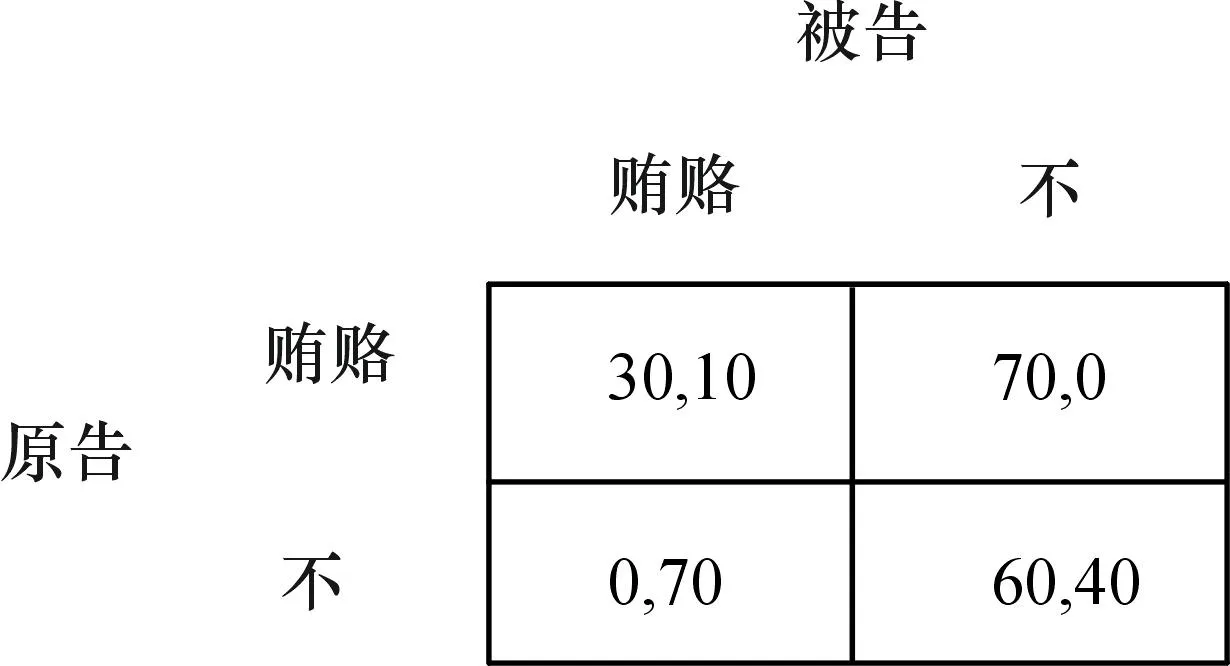
图1

这个博弈中的原告和被告，都有一个占优策略，即不管其对手如何选择，他选择贿赂带来的结果要更好*在《射雕英雄传》中，郭靖用刚学到的“亢龙有悔”这一招对付梁子翁即是如此。。所以，博弈的结局就是，他们两个都会理性地选择贿赂法官(这个行动组合也构成纳什均衡)，然后出现前些年民谣里的结果：“大盖帽，两头翘，吃了原告吃被告。”这个博弈也提示我们，理性的人玩出的结果也许是集体“非理性”，因为(不，不)的结果帕雷托优超(Pareto Dominate)于(贿赂，贿赂)。一个结果帕雷托优超另一个结果，是说从后者到前者没有人受损，但至少有一个人受益，所以我们很难从直觉上否认前者好过后者。

博弈论和纳什均衡可以用来说明一些复杂的社会互动现象。譬如，行动越多结果是否一定越好？图2的博弈中，甲只能选择上和下，其均衡是甲选择上，乙选择右，结果是(50，50)。

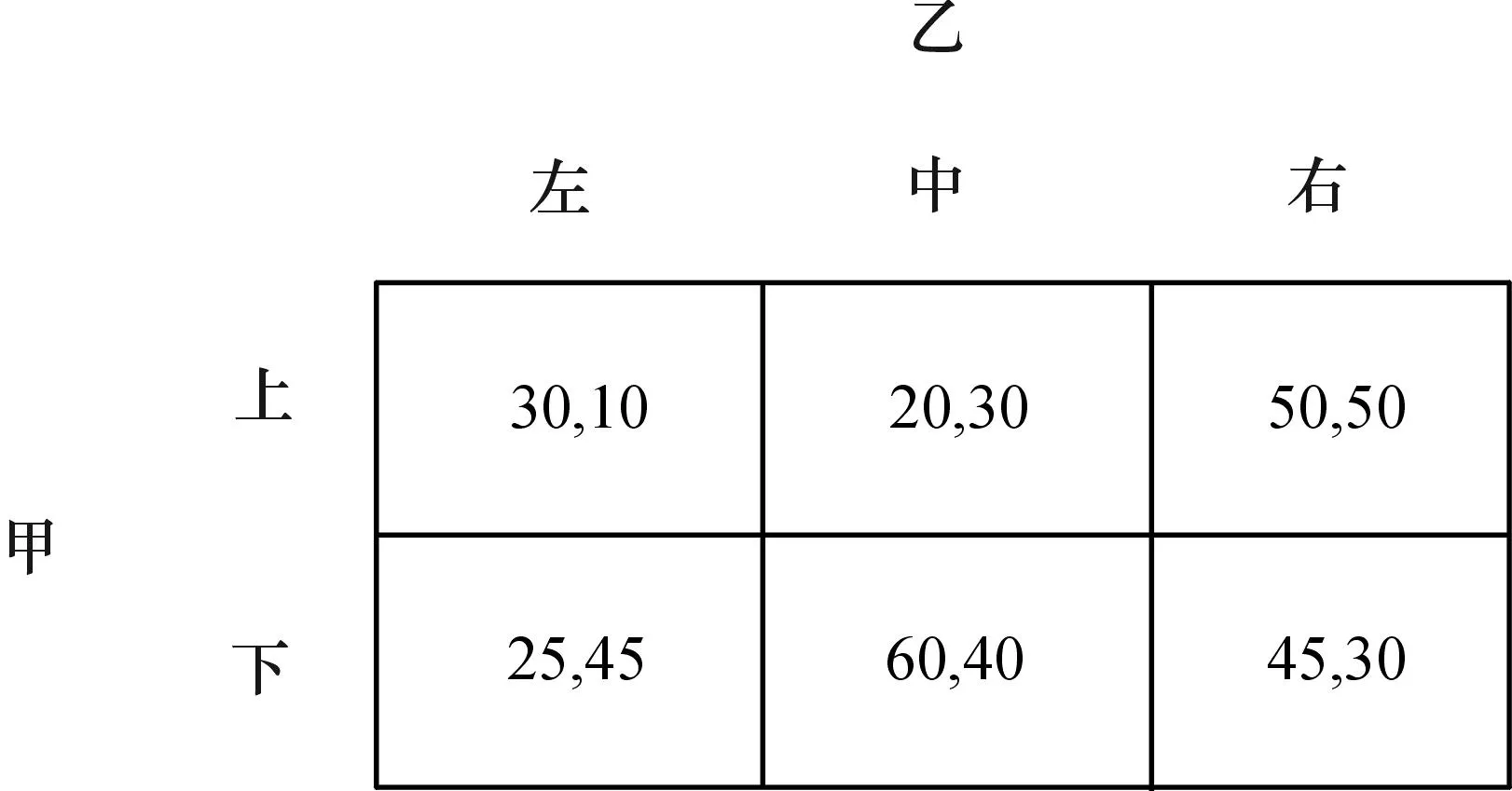
图2

如果甲的行动多(图3)，那么均衡就变成甲选下，乙选左，结果是(40，55)。甲多了一种行动，他的支付却由50缩小到40。

图3

图4的博弈，其均衡是(上，右)，结果是(20，20)。如果甲选择上行动的支付都减少10个单位，博弈就变成图5，其均衡为(下，左)，结果变为(25，15)。甲的“破釜沉舟”反而令其处境改进了。

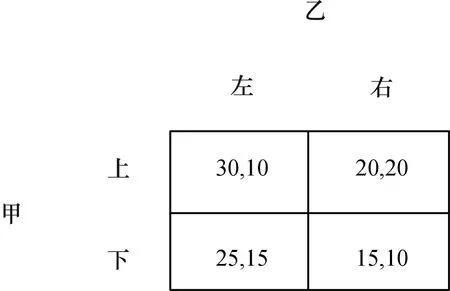
图4

图5

图6的博弈，乙的信息是不完美的，他看不到甲的行动，这实际上是一个同时行动的博弈。它的纳什均衡是(上，右)，结果是(4，4)。

图7的博弈与前面的区别在于，乙能够观察到甲的行动，所以他的信息更充分。但是，更多的信息能否带来更多的支付？

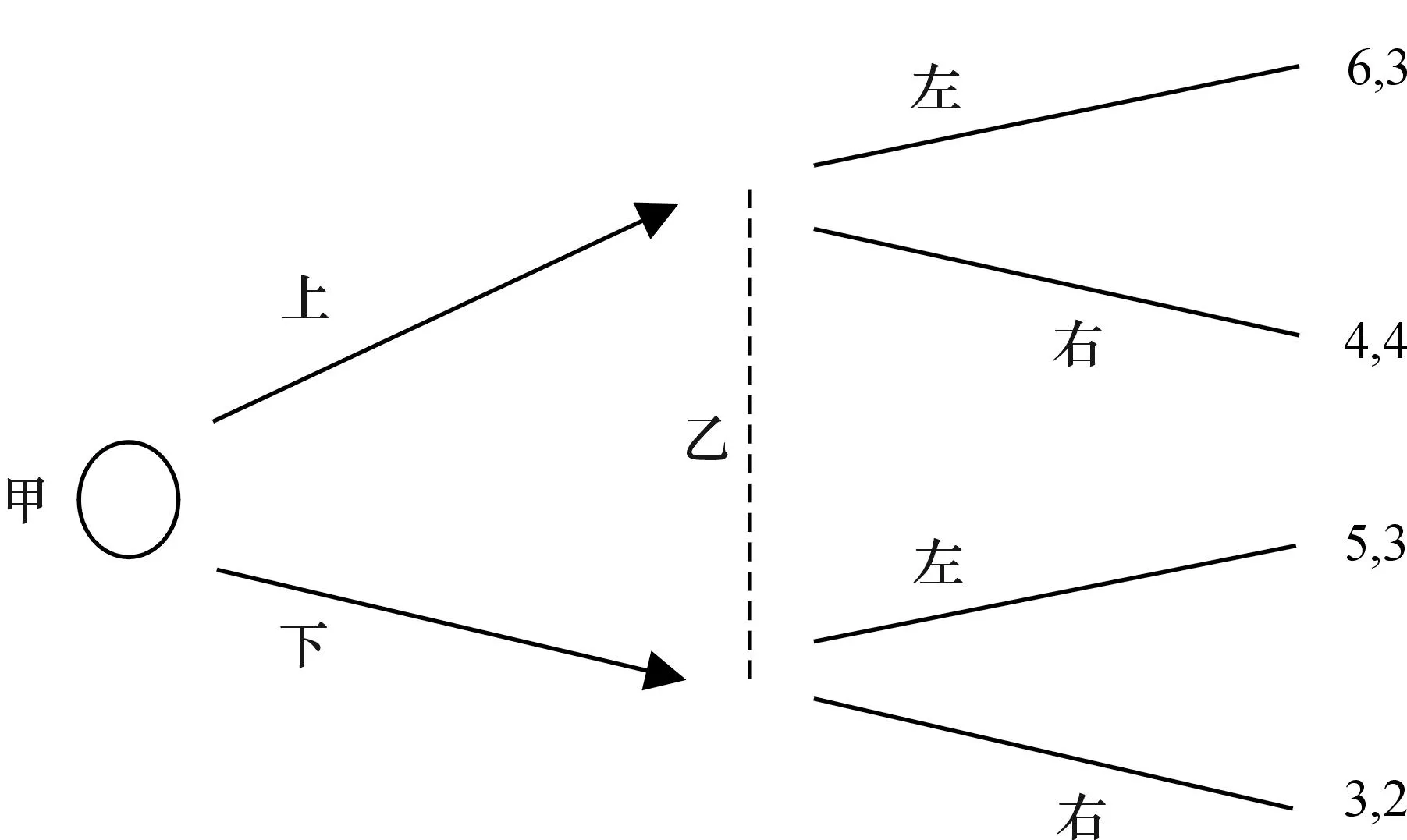
图6

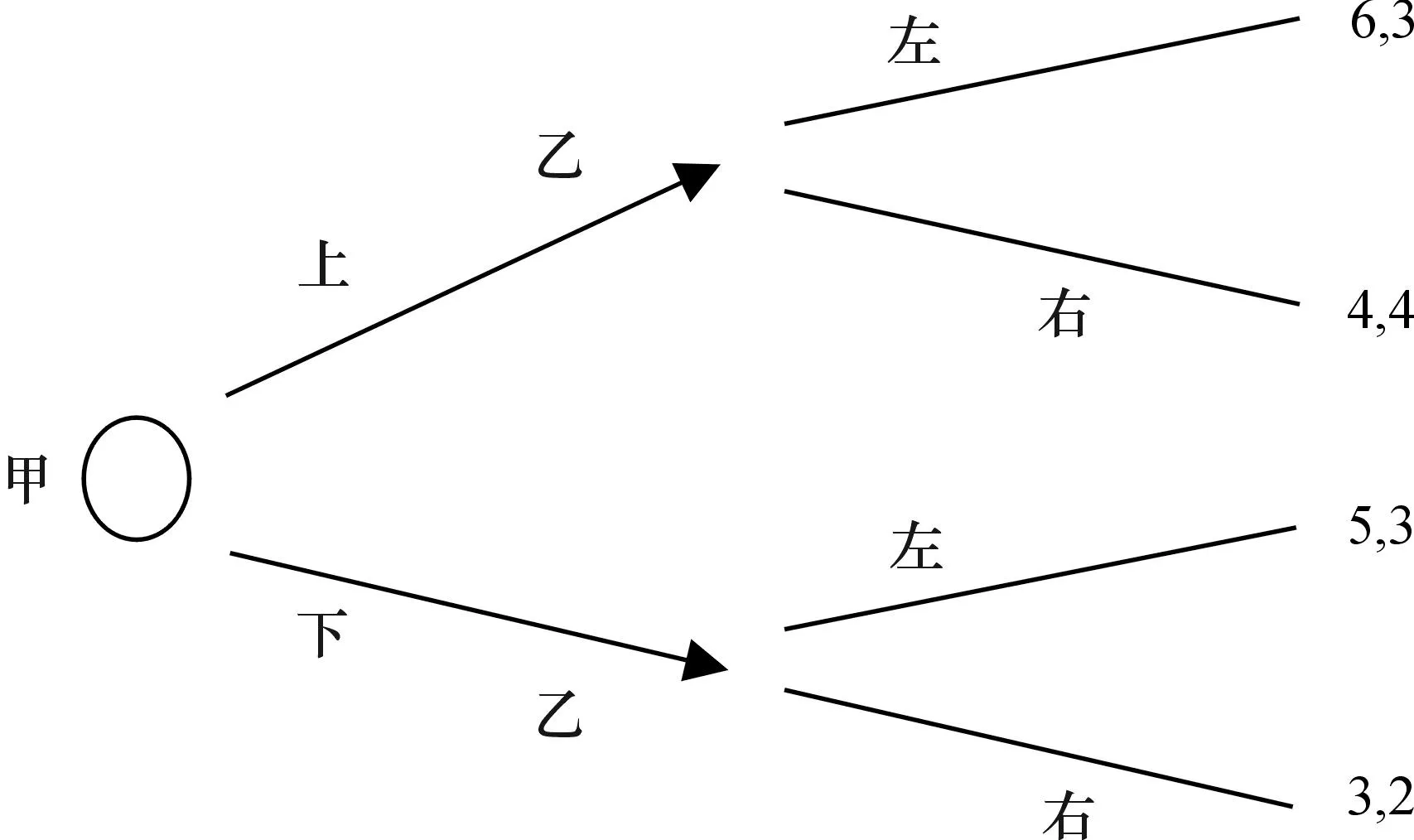
图7

根据逆向递推可知，如果甲选择上，乙会选择右，给甲带来4；如果甲选择下，乙会选择左，给甲带来5。所以甲会选择下，这样结果是(5，3)。两相比较，乙知道的越多得到的越少。

图8是一个绑架博弈，甲绑架了乙，乙劝说甲不要撕票，他保证被放后不会去告发甲。那么甲是否会释放乙呢？根据逆向递推的思想，如果甲放人，那么乙告发比沉默带来更高的效用，所以他会选择告发，从而使甲得到牢狱之灾的-10，这就使其决定撕票。

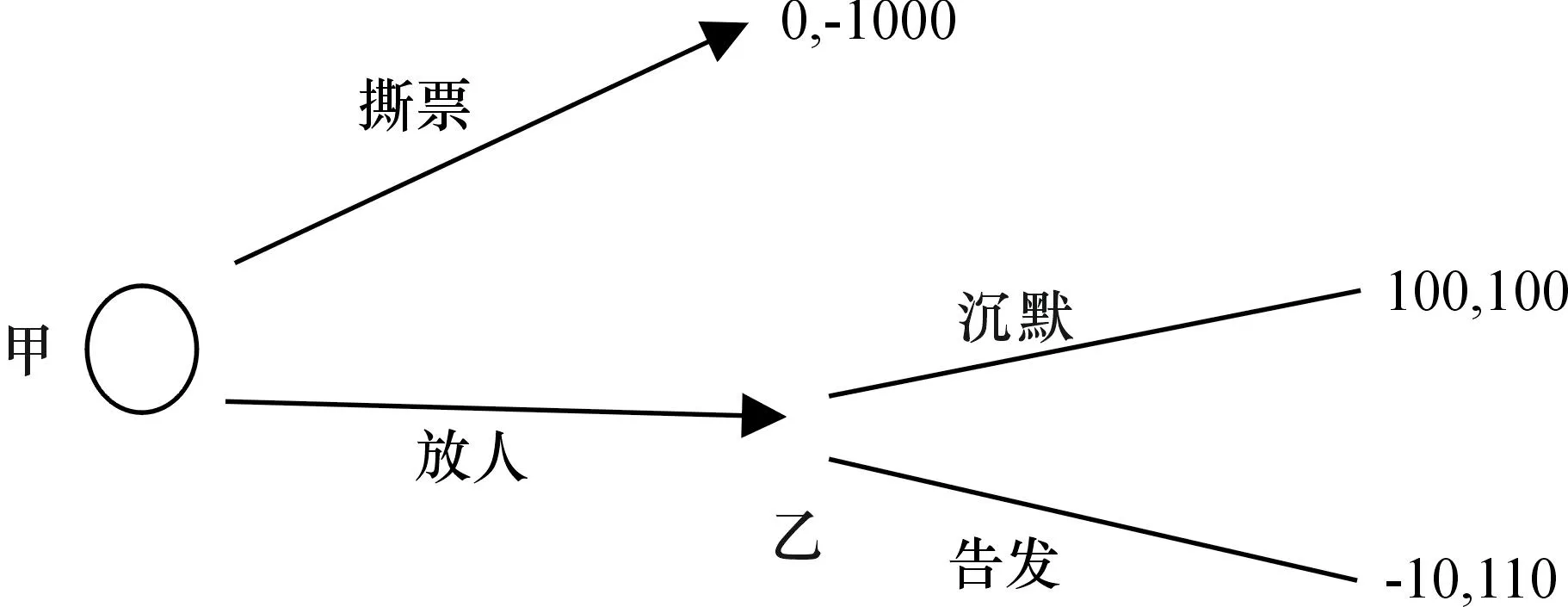
图8

这个博弈中，如果乙告发后由于自己不遵守承诺而忏悔，会使自己的效用降为90，那么博弈的结果就会皆大欢喜了。所以类似的局面，往往因为一个因素发生变化，结局就大相径庭了。当然，其中的博弈之道是不变的。

当然，有的博弈会出现好几个纳什均衡，这就涉及纳什均衡的精炼与筛选问题。如下面的性别战博弈(图9)。女孩子上午逛街回来的路上打电话告诉男友要在哪儿会合，不巧话说一半手机没电了。如果两个人都来到同一个地方，心有灵犀的感觉非常美好，否则就要怀疑是否有缘无分了。那么男孩应该到哪儿等她呢？

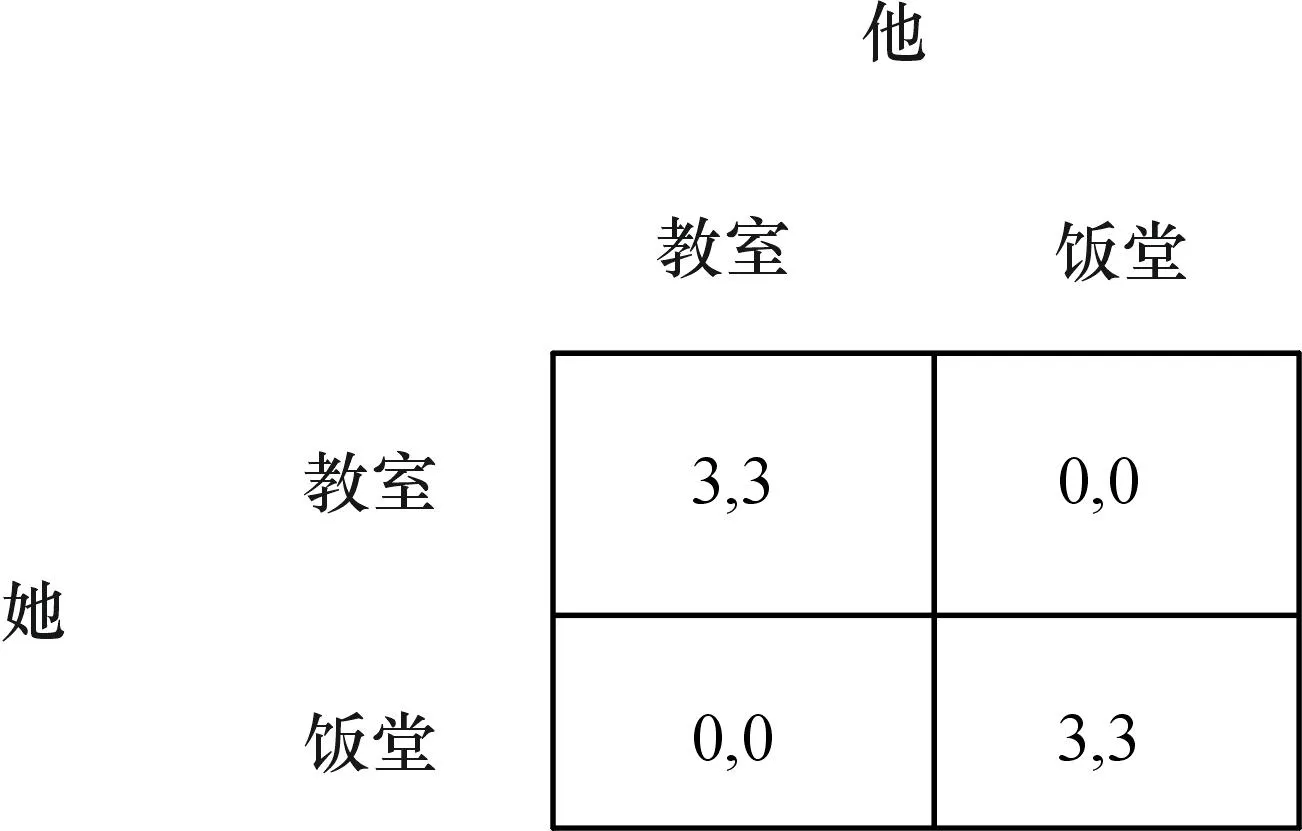
图9

这个博弈有两个纯策略纳什均衡，分别是都去教室或饭堂，和一个混合策略均衡(我们这里不讨论它)。问题不是有没有均衡，而是均衡太多会导致欧亨利(O. Henry)的小说《麦琪的礼物》(The Gift of the Magi)中协调失败的局面(博弈论学者有时就是如此无趣)。谢林(Thomas C. Schelling)的焦点效应理论会告诉我们，一些不影响博弈支付的信息会使得某个均衡更显眼。如果今天是他们在教室认识一周年的纪念日，那么男孩去饭堂就太不解风情了；假如是普通的日子，又快到午餐时间了，等在教室可要被女孩笑骂“爱情不能当饭吃”。

圣经中的所罗门王的故事*以下相关内容主要取自摩尔的综述文章：John Moore. Implementation, Contracts, and Renegotiation in Environment with Complete Information. In Jean-Jacques Laffont (ed.). Advances in Economic Theory: Invited Papers for the Sixth World Congress of the Econometric Society, vol. I. Cambridge University Press, 1992: 182—282.是大家耳熟能详的。但吹毛求疵地说，故事中的假母亲是不够聪明的，如果她和真母亲说同样的话，那所罗门王该怎么办呢？这可以通过一个类似竞标的机制来几乎完美地解决*如果这两个女人是同卵双胞胎姐妹，现代DNA检测技术也无能为力。博弈论学者用此例是为了说明机制设计理论的思想。(图10)。显然，所罗门王不知道谁是真母亲(制度设计者不知道博弈者的个人信息，这是几乎所有机制设计问题都坚持的一个假设，否则问题退化为一个简单的优化问题，他可以强迫执行)，但他知道真母亲比假母亲赋予孩子更高的价值，真假母亲也都知道这点，并且这是一个普遍知识(common knowledge)，即她们都知道每个人都知道这点，她们都知道每个人都知道每个人都知道这点，以至无穷。换言之，她们进行的是完全信息博弈。

所罗门王可以向其中任一母亲(姑且称其为安娜)提问孩子是不是她的。如果安娜说不是她的，那么孩子给另一个女人(可称其为贝莎)，博弈结束。如果安娜说孩子是她的，那么所罗门王可以接着问贝莎是否反对。如果贝莎不反对，则孩子归安娜，博弈结束。如果贝莎反对，则所罗门就要她提出一个赌注v，并向安娜收取罚金。然后，让安娜选择是否愿意与贝莎竞争。如果愿意竞争，那么她要交给所罗门王赌注v那么多钱，孩子给她，同时贝莎也要缴纳罚金F；如果不竞争，那么孩子给贝莎，她给所罗门王赌注的钱v。

图10

因此，我们可以很容易地推出，在安娜是真母亲的情形下，她的策略是说孩子是她的，然后贝莎不反对。因为她反对的结果只会导致她白白缴纳罚金，因为安娜为了得到孩子，必然会真实地根据孩子对她的价值选择竞争；在安娜是假母亲的情形下，她的策略是承认孩子不是她的，因为如果她说孩子是她的，贝莎必然会反对，并且贝莎为了得到孩子一定会选择竞争，而安娜只有报出高于孩子对她的真正价值的赌注才会得到孩子，可这就不合乎她的偏好了。

有人可能会提出疑问，如果假母亲比真母亲更有钱，真母亲却出不起孩子对她所值的钱，这个机制难以起作用。注意到出钱意味着得到孩子付出成本，真母亲可以用愿意“挨多少大板”这样的方式替代出钱，而假母亲依然难以匹配。当然，在假母亲具有妒忌型效用函数时，上述机制就无效了。她可以出很多钱得到一个并不物有所值的东西，只因为这样损害了别人。这种损人不利己的行为，相信大家都知道是很让人头痛的(这是为什么我前面说机制设计可以几乎完美解决这个问题的原因)。相反，如果她再有钱，只要是一个正常的利己主义者，而机制设计者又是依法办事的，那么问题依然好办。

二、博弈论基础

纳什均衡是否一定给出一个博弈合理进行的建议或预见呢？Kreps曾给出一个例子，其中纳什均衡所指派的策略太不合理。两个人同时选择X或Y。若同时选择X，则各得支付1；若一人选X，另一人选Y，则前者得1，后者得0；若同时选择Y，则进入一个报整数比赛。大者得250，小者得100。如果所报数字相同，则各得25。显然，此博弈的子博弈完美均衡是两人同时选择X，各得支付1。但是，他们为什么不同时选择Y而进入报整数比赛呢？其中最差的结果也是远远好于1的25。原因只是，这个报整数的子博弈由于纯策略是无限多的而导致没有纳什均衡存在。如果加上有限性的限制，问题会自然解决。

有哲学趣味的人也许会关心，纳什均衡及其精炼作为博弈的解在何种意义上是合理的?这也正是纳什在他的博士论文附录里所指出的：“在所讨论的博弈中，对理性地进行博弈的可预期的行为的一个合理预测是什么？通过运用一些原则，如一个合理的预测应该是唯一的，参与人应能充分推理和利用知识，并且对于每一个参与人，关于其他参与人行动的知识将不会导致他的行动偏离这个合理的预期。这样我们就得到上面我们定义的解的概念。在这种解释下，我们需要假定参与人了解整个博弈的结构，从而能各自推导出这个预期。这是一个理性和理想化要求很强的解释。”*Harold W. Kuhn and Sylvia Nasar (eds.). The Essential John Nash. New Jersey: Princeton University Press, 2002: 80.

故此，纳什又提出“大众行为”(mass action)的解释：“在经济或国际政治的一些场合，利益集团不自觉地被卷入到一个非合作的博弈之中，这种不自觉使得这个场合变成了一个非合作博弈。在这种解释下，假定参与人对整个博弈的结构有完全的知识或者有能力进行复杂的推理不是必需的。但是我们假定参与人能对他们的各种纯策略的相对益处积累经验性的信息。我们假定存在一定的参与人群并且这些参与人的‘中间分子’运用纯策略有一个稳定的平均频率。”*Harold W. Kuhn and Sylvia Nasar (eds.). The Essential John Nash.New Jersey: Princeton University Press,2002:78.

纳什的洞察预示着20世纪后期关于博弈论基础的研究，即宾莫尔所强调的演绎(eductive)的与进化(evolutive)的均衡化过程。知识论与进化论关于博弈论解概念的解释与论证是互补的。前者对应着纳什均衡在规范意义上是任何一种理性决策理论的合理内核；后者对应着纳什均衡在实证意义上只能看作是对一种在进化过程中稳定下来的行为模式的近似刻画。

知识论基础的要求，如博弈结构、解理论是博弈者之间的共同知识，不受限制的计算能力等是如此之强,以致于我们很难认为它是现实的。但是，正如韦布尔(Jörgen W. Weibull)所指出，如果我们能够表明博弈者“好像是(as if)”具有很好的理性和知识一样行为的，那么这就为研究者采取这样一种描述世界的方式提供了合理性辩护。从长期(long-run)或大范围来看，进化博弈理论(包括学习理论)的博弈者通过学习和进化，他们的行为模式在统计或极限意义上是什么，以此为各种解概念下的理性行为提供合理化论证。特别地，针对纳什均衡及其各种精炼，有众多结果刻画了在什么条件下，均衡解可以看作是进化和学习的收敛或统计意义上的近似，即佩顿·杨(Peyton Yong)所谓:“高理性的解概念能够从低理性的环境中涌现，如果我们赋予这个过程足够的时间进化。换句话说，社会反馈机制可以取代在个体方面的知识和推理能力的高水平。”此外，通过进化博弈及其应用社会生物学，我们发现博弈论和纳什均衡的思想与方法可以有更广阔的应用天地。

三、纳什谈判解与纳什规划

现在，我们转向纳什的另一项贡献——谈判或讨价还价理论。在纳什的基本定理之前，他在1949年已经有了一项了不起的经济学成果。作为读大学时选修的一门国际贸易课程的产物，他讨论了交易中分配合作利益的讨价还价问题，并给出了有关的纳什谈判解的公理刻画。如果二人进行一个谈判，有一组备选方案，也有一个协议未成点或现状是大家的退路。达成的分配方案应该具有这样几个好的性质(我们这里的表述本质上与纳什当年没有差异)：谈判是有效率的，即不存在另一个备选方案帕雷托优超于达成共识的；谈判是非强迫性的，每个人都应不差于协议未成点；不相关方案的独立性，如果某方案是一个谈判问题的解，现在缩小方案范围但它仍在其中，则它依然是新谈判问题的解；对称性，如果有倾向于甲的方案就有同样对乙有利的方案，并且二人的退路相同，那么结果应该是二人所得相同。加上其他一些数学上的适当条件，纳什证明，合理的解应该最大化二人的净支付的乘积。

在三年后的文章中，纳什还提出了现在所谓的纳什规划，以打通非合作博弈与合作博弈之间的关系。如奥斯本(Martin J. Osborne)与鲁宾斯坦(Ariel Rubinstein)所指出的：“结盟模型区别于非合作模型本质上是因为，它把重点放在博弈者团体能实现什么而不是单个博弈者能做什么上，并且它不考虑博弈者团体内部是如何作用的。如果我们希望在一个非合作博弈中模拟结盟形成的可能性，那么我们必须叙述结盟是如何形成的以及他们的成员是如何选择加入的。一个结盟博弈没有这些细节，这样一个博弈的结果也不依赖于它们。”*Martin J. Osborne and Ariel Rubinstein. A Course in Game Theory. Massachusetts: MIT Press, 1994: 255—256.这样，囚徒困境博弈所谓的困境在合作博弈中就不可能出现。但合作博弈却不存在像非合作博弈中的纳什均衡及其精炼等具有统一性的解理论。纳什提出，合作博弈的解，可以归结为谈判解，而谈判问题又可以转换成一个动态的非合作博弈，这样就可以用非合作博弈的解概念来重新阐释合作博弈的各种解概念。纳什规划的后续研究包括了鲁宾斯坦的重要工作，他表明纳什谈判解可以由一个无限期动态讨价还价博弈的子博弈完美均衡来得到。在这个意义上，非合作博弈比合作博弈更为基本。当然，现在大部分学者会公允地认为，合作博弈与非合作博弈是一枚硬币不可分割的两面。而纳什规划实质上还蕴涵着，几乎所有冲突与合作的局面都可以经由纳什均衡的思想得到合理的描述与解释。

巧合的是，宾默尔的教科书《游戏与博弈》(Fun and Games)中提到，纳什名字的拼写NASH代表了博弈论的英雄榜。*Ken Binmore. Fun and Games: A Text on Game Theory. Lexington Massachuesetts：D. C. Heath and Company, 1992: 13.其中最杰出的贡献者有：N指博弈论的创始人冯诺依曼和纳什，A是奥曼(Robert J. Aumann)，S代表了沙普利(Lloyd S. Shapley)、泽尔腾和谢林，H则是豪尔绍尼。如果说，纳什的名字由于偶然被用于构成博弈论圣殿建造者的谱系(实际上杰出的博弈论学者的名单非常长)，那么我们可以毫无疑问地说，纳什均衡是非合作博弈论最重要的解概念大厦的基石。迄今为止，几乎所有因博弈论获得诺贝尔经济学奖的理论贡献都与纳什的工作有一定的关联。其中，豪尔绍尼、纳什与泽尔腾1994年一起获奖；此外，2005年奥曼和谢林，2007年赫维茨(Leonid Hurwicz)、马斯金(Eric Maskin)和迈尔森(Roger B. Myerson)，2012年沙普利和罗斯(Al Roth),1996年米尔利斯(J. A. Mirrlees)和威克瑞(William Vickery)，2001年阿克洛夫(George A. Akerlof)、斯宾塞(A. Michael Spence)和斯蒂格里茨(Joseph E. Stiglitz)，2009年奥斯特罗姆(Elinor Ostrom)，2014年梯若尔(Jean Tirole)，他们的获奖工作都运用了博弈论。实际上，2002年的行为与实验经济学，2010、2011年的宏观经济理论，2013年的证券理论，也都或多或少地与博弈论有关。

四、不朽的思想

协助纳什发表那个运用了角谷静夫不动点定理(Kakutani Fixed-point Theorem)的简单证明版本(1950年发表于《美国国家科学院院刊》)的盖尔(David Gale)，曾经赞叹纳什成果的优美和普遍性(elegance and generality)，而且所有伟大的智力成果，都具有这两个特征。爱因斯坦曾经说过，如果一个理论不美，它就不会是真的。从数学和自然科学，以及从牛顿、达尔文、爱因斯坦、哥德尔和无数先贤的经典作品中，我们都能感受到这种简单、纯净而深刻的美感。而普遍性，或者说普适性和统一性，是好的理论最重要的品质。

可以说，作为一个体现了形式简洁性与内容丰富性的折中的解概念，纳什均衡是整个博弈论的核心。因机制设计理论获奖的迈尔森将纳什均衡比之为生物学中的DNA双螺旋结构。正如1998年诺奖得主森(Amartya Sen)所言，博弈论和社会选择理论(二者的结合产生了机制设计理论)是二次世界大战以后社会科学领域最重要的成果。纳什均衡和帕雷托优超，作为博弈论和社会选择理论中两个最重要的概念，则构成了现代社会科学大厦的拱柱。我相信，只要人类社会中的冲突和合作现象继续存在，社会科学继续存在，这两个概念及其思想将会是不朽的。

按照迈尔森的说法，今天我们可以更宽泛地把经济学定义为“对所有社会制度中的激励(incentive)的分析”，从而“社会科学的功能性目标并非仅仅在抽象意义上预见人类行为，而是分析社会制度和评价关于制度革新的建议”。那么，一个制度目标要得以实现，必须使其所对应的行动成为社会博弈的纳什均衡。由于纳什“表明任何其他博弈理论都可以被化归到均衡分析”，因此，他“把社会科学带入到一个新世界，那里可以发现一个研究所有冲突与合作局面的统一分析框架”。*Roger B. Myerson. Nash Equilibrium and the History of Economic Theory. Journal of Economic Literature, 1999, 37: 1068,1069,1074.

参考文献：

[1]KEN BINMORE. Fun and Games: A Text on Game Theory. Lexington Massachuesetts：D. C. Heath and Company, 1992.

[2]ERIC VAN DAMME. Stability and Perfection of Nash Equilibrium, Second and Enlarged Edition. Berlin Heidelberg: Springer-Verlag, 1991.

[3]ROGER B. MYERSON.NashEquilibriumandtheHistoryofEconomicTheory. Journal of Economic Literature, 1999, 37: 1067—1082.

[4]JOHN F. NASH.EquilibriumPointsinN-personGames. Proceedings of the National Academic of Science, 1950, 36: 48—49.

[5]JOHN F. NASH.TheBargainingProblem. Econometrica, 1950, 18: 155—162.

[6]JOHN F. NASH.Non-cooperativeGames. Annals of Mathematics, 1951, 54(2): 286—295. Also in Harold W. Kuhn and Sylvia Nasar (eds.). The Essential John Nash, with Appendix: Motivation and Interpretation. New Jersey： Princeton University Press, 2002.

[7]JOHN F. NASH.Two-personCooperativeGames. Econometrica, 1953, 21: 128—140.

【责任编辑：王建平、肖时花】

(作者简介:丁利，山东莱西人，法学博士、经济学博士后,中山大学法学院副教授。)

【中图分类号】O225

【文献标识码】A

【文章编号】1000-5455(2016)02-0005-07

【收稿日期】2016-02-20

【基金项目】国家社会科学基金重点项目“全面推进依法治国的逻辑理性根基研究”(13AZX017)；2013年广东省“法治化进程中的制度设计与冲突解决”项目(1314006-12000-4225021)

编者按：约翰·纳什(John Nash，1928—2015)，美国著名经济学家、博弈论创始人，前麻省理工学院助教，后任普林斯顿大学数学系教授，主要研究博弈论、微分几何学和偏微分方程。1950年，纳什以非合作博弈(Non-cooperative Games)为题获得美国普林斯顿高等研究院的博士学位。他在这篇仅仅27页的博士论文中提出了一个重要概念，也就是后来被称为“纳什均衡”的博弈理论。1994年，由于纳什在非合作博弈均衡分析理论方面做出的开创性贡献，及其对博弈论和经济学产生的重大影响，他和其他两位博弈论学家共同获得了当年的诺贝尔经济学奖。2015年5月23日，约翰·纳什在美国新泽西州不幸逝世，终年86岁。为纪念纳什逝世一周年，本刊特推出此文，以飨读者。