舰船机动中拖曳系统建模与定深控制研究

郑智林，苑志江，金良安，谢田华

(海军大连舰艇学院 航海系,辽宁 大连　116018)



舰船机动中拖曳系统建模与定深控制研究

郑智林，苑志江，金良安，谢田华

(海军大连舰艇学院 航海系,辽宁 大连116018)

摘要：针对拖曳系统在舰船机动过程中拖体深度产生复杂变化的问题，考虑拖曳系统运动和舰船操纵之间相互作用，建立了相应的耦合数学模型。舰船采用经典的MMG模型，拖缆和拖体的动力学模型分别采用有限差分法和水下运载器的六自由度运动方程。采用数值计算方法，获得了系统在舰船机动过程中的响应，并运用经典PID算法，通过控制拖体水翼的攻角，实现了拖体在舰船机动过程中的目标深度控制。仿真结果表明这一方法正确有效，具有一定的理论意义和工程应用价值。

关键词：拖曳系统；舰船机动；定深控制；数值仿真

随着水下拖曳系统在军事和海洋研究等领域应用的日渐广泛，尽快丰富完善其相关基础性研究尤为紧迫，特别是舰船机动中拖曳系统控制理论的研究。水下拖曳系统因其拖缆长度有限而致拖体距舰船很近，拖体工作在复杂的船尾湍流中，尤其当舰船机动时，拖体、拖缆、舰船三者之间相互影响更为复杂，使拖体深度与姿态的控制更难保证。

国内外学者目前对水下拖曳系统在舰船机动中的运动响应和水下拖曳系统运动中拖体的定深问题，分别做过大量的研究[1-3]。但是，考虑舰船机动过程对拖体深度的影响，在三维空间中实现拖体定深的相关研究很少。

本文研究的水下拖曳系统在舰船机动中的定深控制，以削弱舰船航速变化和回转运动等对拖体深度影响作为目标，通过控制拖体水翼攻角实现目标深度的定深功能。考虑拖曳系统运动和舰船操纵之间的相互作用[4]，建立将舰船的操纵方程和拖曳系统的运动方程耦合的数学模型。采用经典的MMG模型和有限差分法描述舰船和水下拖缆的动态运动，同时基于水翼理论构建配置控制水翼的拖体六自由度运动模型。在此基础上结合三者的耦合运动和动力边界条件[5-6]，建立完整的数学模型。通过数值仿真模拟分析整个系统在舰船各种机动条件下的运动响应特性，并运用经典PID控制算法控制拖体水翼攻角，实现在舰船机动中对拖体的目标深度定深控制。

1系统运动数学模型

1.1坐标系

为描述水下拖曳系统的运动特性，引入4个右手坐标系，即惯性坐标系(i,j,k)，i方向与舰船初始航行方向相同，k方向为垂直向下；舰船随体坐标系(is,js,ks)，is方向为舰船重心指向舰船首部，js平行于基面指向舰船右舷，ks指向舰船底部；拖缆局部坐标系(t,n,b)，位于缆索的每个点上，t为拖缆的切线方向，n和b为两个法向向量且b在i和j的平面内；拖体随体坐标系(iv,jv,kv)，三个轴向的方向定义与舰体随体坐标系一致。四个坐标系的方向如图1所示。

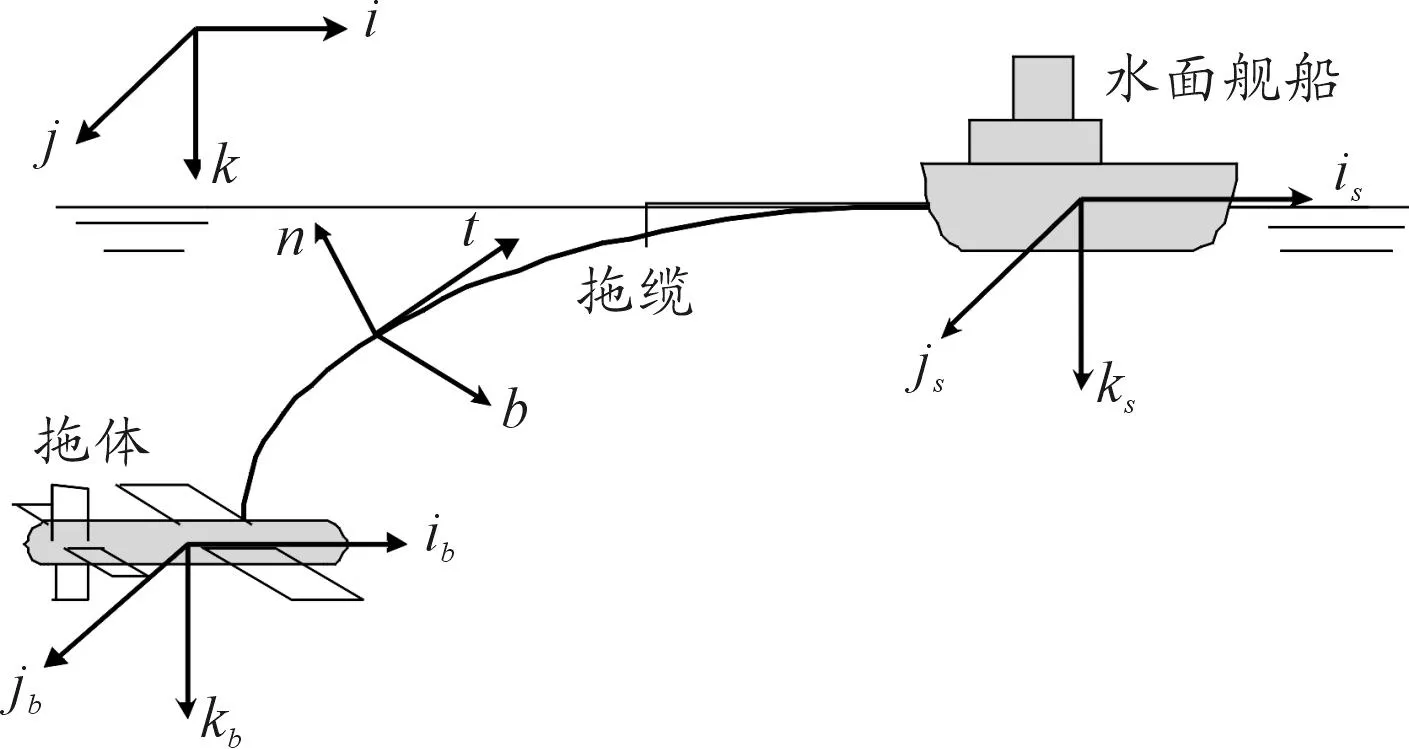
图1　水下拖曳系统

1.2舰船操纵运动控制方程

舰船运动控制方程借鉴分离式MMG操纵运动数学模型[7]，即舰船在桨、舵操纵下的四自由度(纵向、横向、横倾、艏向)的运动控制方程

(1)

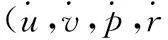
舰体、螺旋桨、舵的水动力详见文献[7]，这里不再详述。拖缆顶端的张力在拖缆局部坐标系下的表达式为TC=[TC0 0]T，则作用在舰船的拖缆顶端张力和力矩在舰船随体坐标系下的表达式为

(2)

式中：R(φ,θ,ψ)为船体坐标系与惯性坐标系之间的旋转矩阵；D为拖缆局部坐标系与惯性坐标系之间的转换矩阵；rC为拖缆顶端点在舰船坐标系下的位置。

1.3拖缆运动数学模型

拖缆的运动方程[8]参考Ablow模型。假设拖缆是细长、柔软和圆柱形状，缆上任意点所受拉力随时间变化。拖缆上受重力、水动力和惯性力作用，其任意点的力平衡方程可表达如下

(3)

式中：S为拉伸后拖缆的弧长；W为单位长度拖缆在水中的重力和浮力之差；F为单位揽长受到的流体水动力；B为单位长度缆绳受到的惯性水动力。

经过推导，拖缆系统的动力学方程写成如下矩阵形式[6]

(4)

式中：y(s,t)=[TVtVnVbαβ]T，其中t表示时间，s表示拖缆未拉伸时的弧长，T为张力，Vt、Vn和Vb为拖缆局部坐标系下的三个速度分量；α和β为拖缆局部坐标相对于惯性坐标之间的方向角。

拖缆局部坐标系(t,n,b)与惯性坐标系(i,j,k)与之间的转换关系为

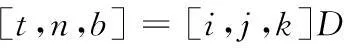
(5)

式中D为拖缆的局部坐标与惯性坐标之间的转换矩阵[3]。

将拖缆上任一点的位置对缆长求导

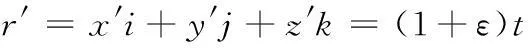
(6)

即可得拖缆上任意一点惯性坐标(x,y,z)的微分表达

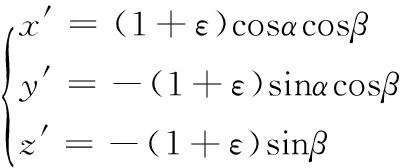
(7)

当应变ε和角度α和β已知时，可对揽长s积分求(x,y,z)。

1.4拖体运动数学模型

拖体的运动主要是垂向运动和纵向运动的合成，表现为六个自由度的运动，分别为轴向、横向、垂向、横滚、俯仰和偏航。根据拖体受力分析和平面运动方程，水下拖体空间六自由度的一般方程如下[9]：

(8)

式中：m为拖体质量；Ix、Iy和Iz为拖体质量惯性矩；Ixy、Iyz和Ixz为拖体交叉惯性矩； (xG,yG,zG)为定义在拖体随体坐标系上的拖体重心坐标。方程右边项F=(X,Y,Z)和M=(K,M,N)为作用于拖体上的外力和外力矩，包括回复力(重力和浮力合力)Fw、惯性附加力FI、黏性力FV、拖缆的末端张力FT以及水翼控制力FC和各力相对应的力矩

(9)

上述除水翼控制力FC外的各力的计算方法与Jiaming Wu[10]中算法大致相同，下面主要确定水翼控制力FC和其对应的力矩MC在拖体随体坐标系下的表达式。

拖体的水翼控制力主要表现为改变水翼攻角时产生的升力和阻力，其表达式如下

(10)

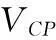
在系统运动过程中，当控制水翼开始工作时，假设水平翼和垂直翼给定的控制攻角分别为δr和δs，则两者的有效攻角为

(11)

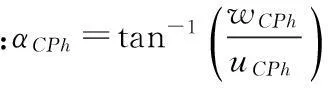
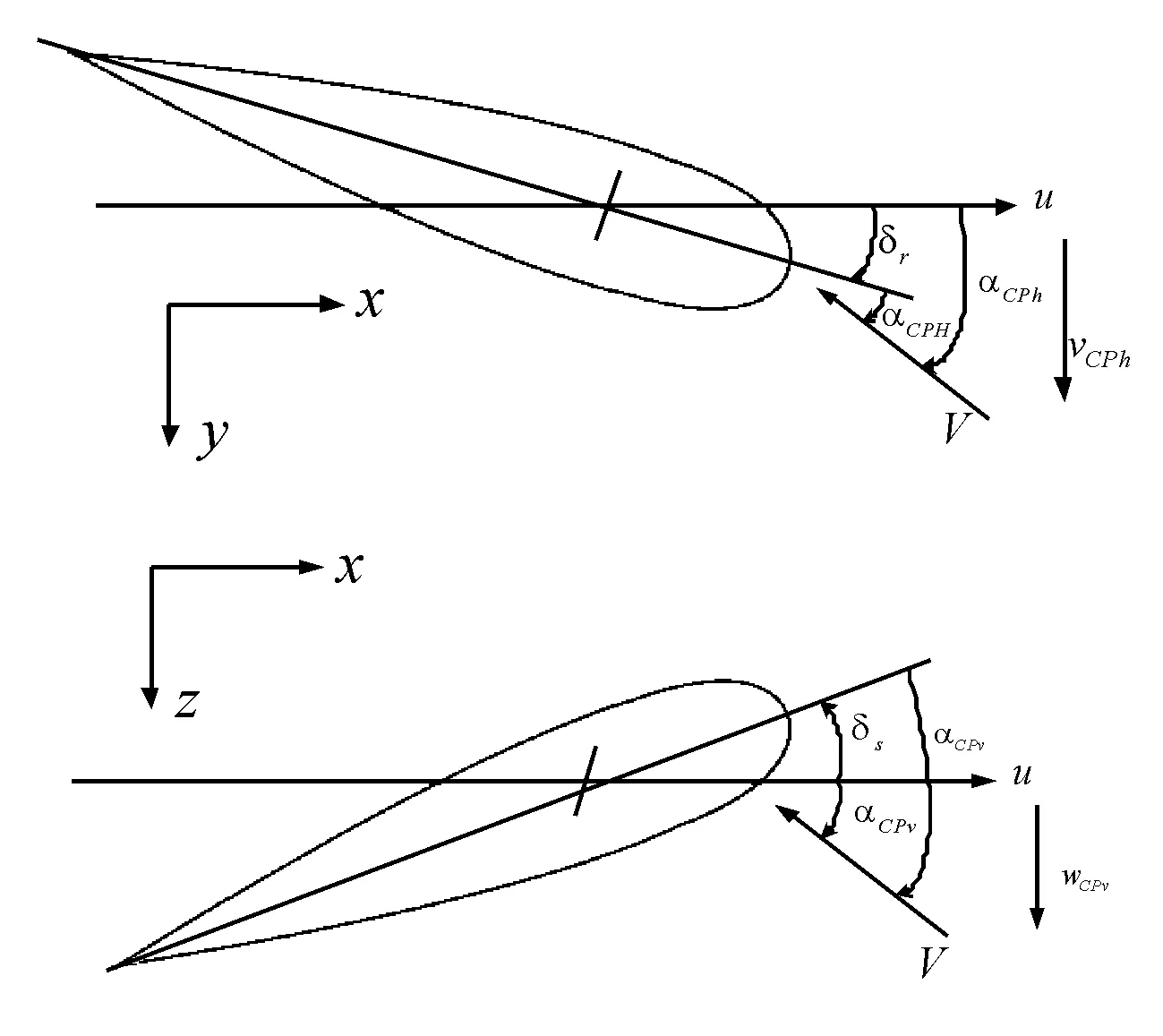
图2　控制翼有效攻角示意图

经过推导，可得水平翼产生的控制力和力矩在拖体随体坐标系下表达式为

(12)

垂直翼产生的控制力和力矩在拖体随体坐标系下表达式为

(13)

由式(12)、式(13)，可得拖体在控制水翼的作用下所受的控制力和力矩为：

(14)

1.5系统耦合边界条件

在水下拖曳系统运动过程中，舰船、拖缆和拖体之间是相互作用、相互影响的。建立数学模型时，本研究以舰船拖点处和拖体拖曳点的速度分别和拖缆首末端的速度相同作为运动耦合边界条件，建立边界条件方程。首先，舰船拖点处的航行速度和拖缆首端节点的速度相同，即

(15)

式中：Vs、ωs分别为舰船原点在舰船运动坐标系下的速度和角速度；rsc为拖缆首端节点在舰船运动坐标系中的位置；Vst为拖缆首端节点在拖缆局部坐标系下的速度。

其次，拖体上拖曳点的速度与拖缆末端节点的速度相同，即

(16)

式中：Vv、ωv分别为拖体原点在拖体运动坐标系下的速度和角速度；rvc为拖缆首端节点在拖体运动坐标系中的位置；Vvt为拖缆末端节点在拖缆局部坐标系下的速度。

1.6系统运动模型的数值求解方法

由舰船运动方程(1)联立拖缆运动方程(4)、拖体运动方程(8)及边界条件(15)、边界条件(16)可组成整个系统完整的偏微分运动控制方程组。针对这一非线性数学方程组，无法直接求得其解析解，可采用数值求解的方法进行求解。

本研究在拖缆有限差分法的基础上，将舰船和拖体运动方程在时间域上也进行中心差分，将整个系统模型中的偏微分方程和微分方程均变为差分方程的形式，形成非线性方程组，进而使用Newton迭代法求解。

2拖体定深PID控制策略

拖体主要的升力来自其主体和控制水翼，通过改变控制水翼的攻角可以提供变化的升力，使拖体在水中上升或者下降。假设拖体各个方向的运动只与本方向所受的力和力矩有关，与其他方向的力和力矩无关，将拖体的运动控制简化为多个单输入单输出的类型，即可以采用经典PID控制。

拖体定深PID控制模型框图如图3。PID控制系统的输入为上一时刻拖体深度与目标深度之差zd，输出为应该给拖体垂向施加的外力Fz。水翼攻角控制系统输入为Fz，输出为控制水翼这一时刻的攻角θ。PID控制系统离散方程为

(17)

式中：T为采样周期；ze(n-1)和ze(n)为第n-1次和第n次采样所取得的深度差；Kp、Ki、Kd分别是比例系数、积分系数、微分系数。

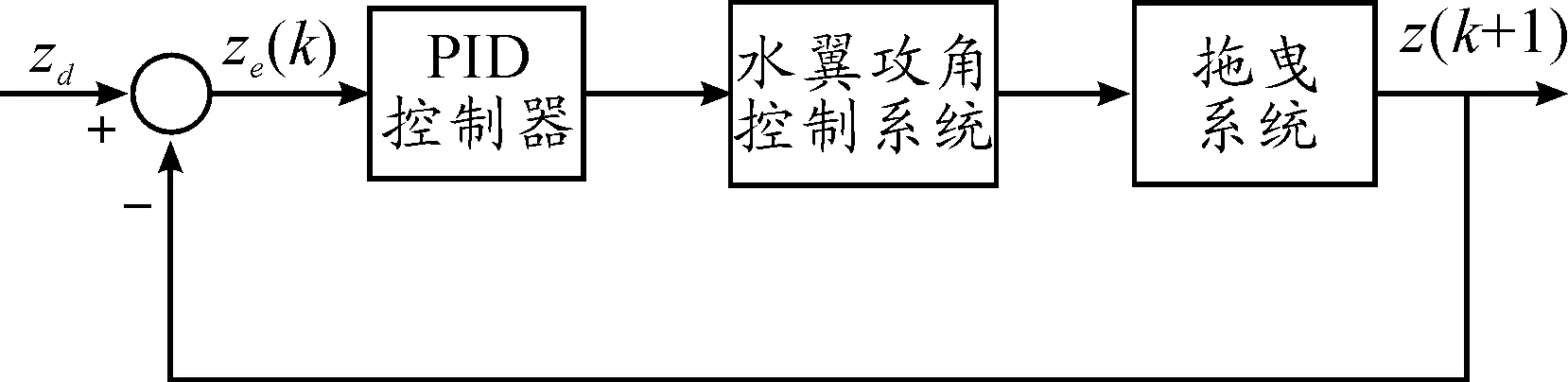
图3　PID控制模型框图

由式(17)计算出某时刻应该给拖体垂向施加的外力Fz后，由式(10)～式(13)可得算出该时刻水翼加的控制攻角δ。

拖体在接收到舰船发出的控制指令后控制系统开始工作，由拖体上的测量装置实时测得拖体的位置和姿态信息，通过不断改变水翼的攻角改变拖体的升力，从而改变拖体的垂向速度，使拖体向目标深度接近。在拖体目标深度的距离减小时，垂向速度也随之减小，并在达到目标深度时速度为零。整个控制过程在舰船发出控制指令后由拖体上计算机完成。

3仿真结果

为实现在舰船机动中对拖体进行目标深度的定深控制，本研究建立了耦合舰船运动的水下拖曳系统三维仿真系统，进行了一系列的仿真计算。计算程序所用的一些主要参数如表1所示。

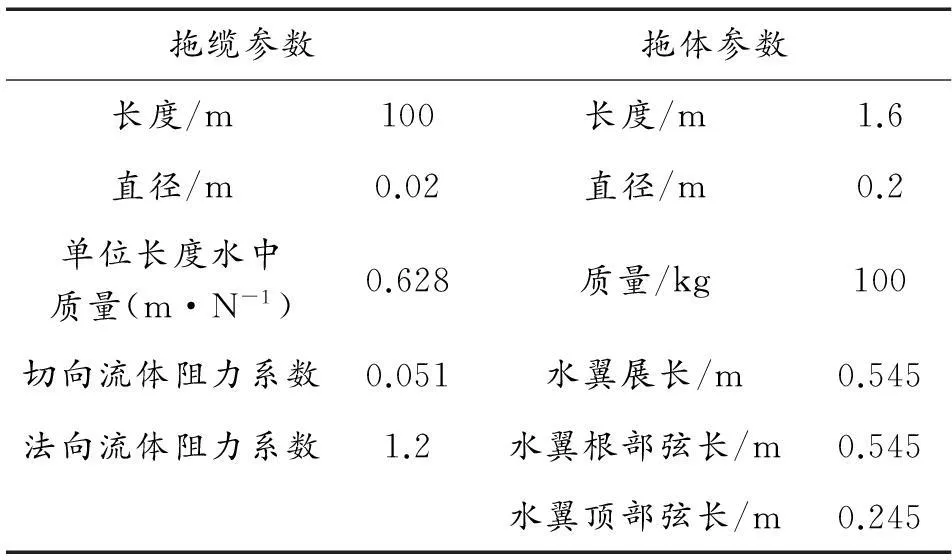
表1　水下拖曳系统参数

3.1直线航行稳定状态与控制

假设整个水下拖曳系统处在静水中，系统在舰船的拖带下匀速直线运动，则舰船的螺旋桨转速分别为40 r/min、60 r/min 和80 r/min时的稳态运动速度如表2所示。

表2　不同螺旋桨转速时水下拖曳系统的速度

不同螺旋桨转速下，拖缆的稳态缆形姿态变化情况如图4所示。结果显示，舰船拖曳速度越快，拖曳系统的拖曳倾角和拖体稳定深度越小，这与实际情况相符。同样的条件下，通过PID控制水翼(PID参数Kp=1.03，Ki=3，Kd=0.01)，水翼开始工作以后，目标深度为20 m时拖体深度随时间的变化如图5所示。

图4　不同拖曳速度下系统的稳态缆形

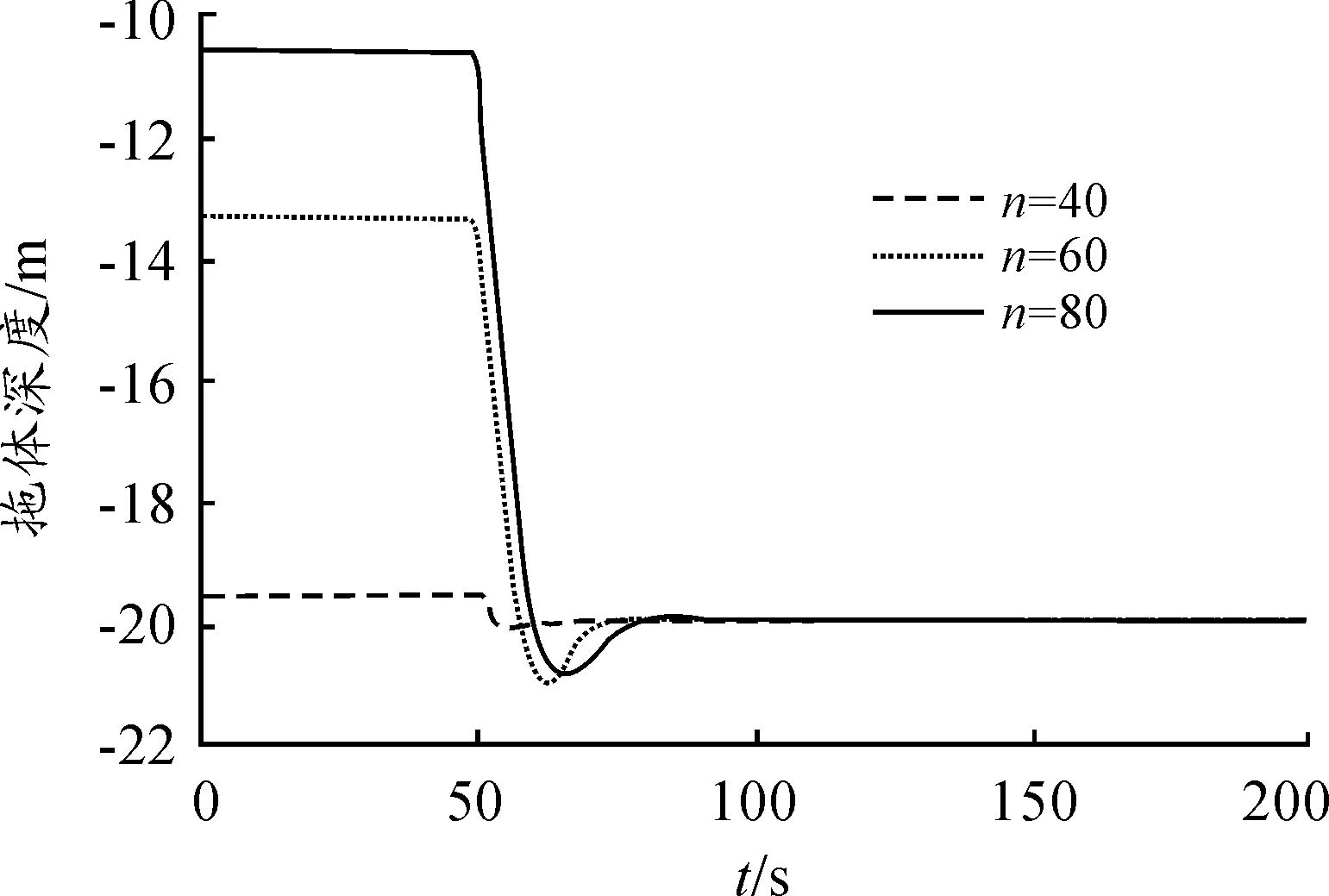
图5　控制过程中拖体深度变化

图4、图5表明，舰船拖曳速度的变化，对拖曳系统稳定时拖缆的姿态和拖体的稳定深度有较大的影响。但在控制水翼的调节下，拖体能在较短时间内达到目标深度，并稳定运动。

3.2直线航行加速运动与控制

舰船螺旋桨先以40 r/min转速直线航行，待拖曳系统稳定后，将转速调为60 r/min，加速过程中舰船速度变化过程如图6所示。而无水翼控制时，拖体深度变化过程如图7所示，其变化趋势与图6中舰船加速中速度的变化趋势保持一致，此结果表明，舰船的加速过程会引起拖体深度的变化。

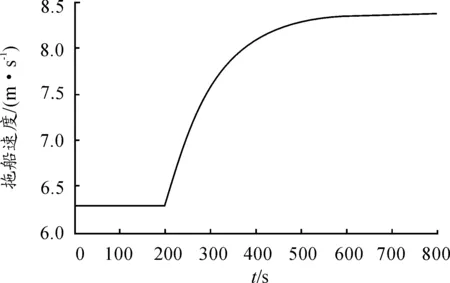
图6　舰船速度

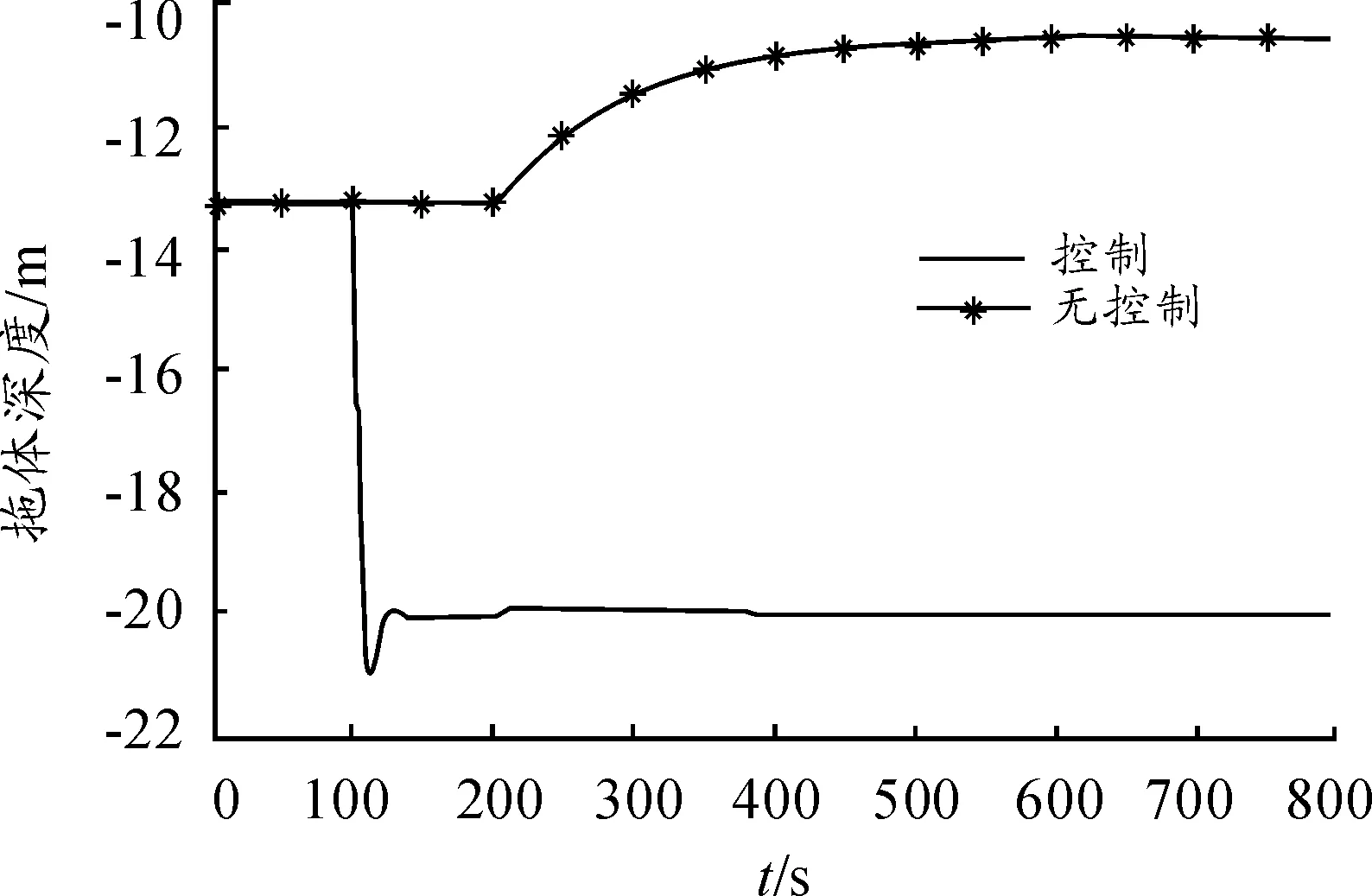
图7　拖体深度变化

图7的结果显示，在水翼控制下(PID参数Kp=0.72，Ki=1.8，Kd=0.05)，可使拖体的深度稳定在目标深度20 m。当水翼不工作时，拖体深度变化幅度大(数值计算结果为2.7 m)；而水翼工作时，其幅度仅为0.15 m。因此，通过控制拖体水翼的攻角能有效地削弱舰船加速过程对拖体深度的影响，使拖体在目标深度稳定地工作。

3.3回转运动与控制

图8为舰船进行回转运动时，通过控制水翼实现拖体的定深控制(目标深度为20 m)。舰船以40 r/min的转速直线航行，在200 s的稳定运动后，以舵角为0.3 rad开始回转运动，在1 310 s 结束回转运动，继续沿末端切线方向直线航行。

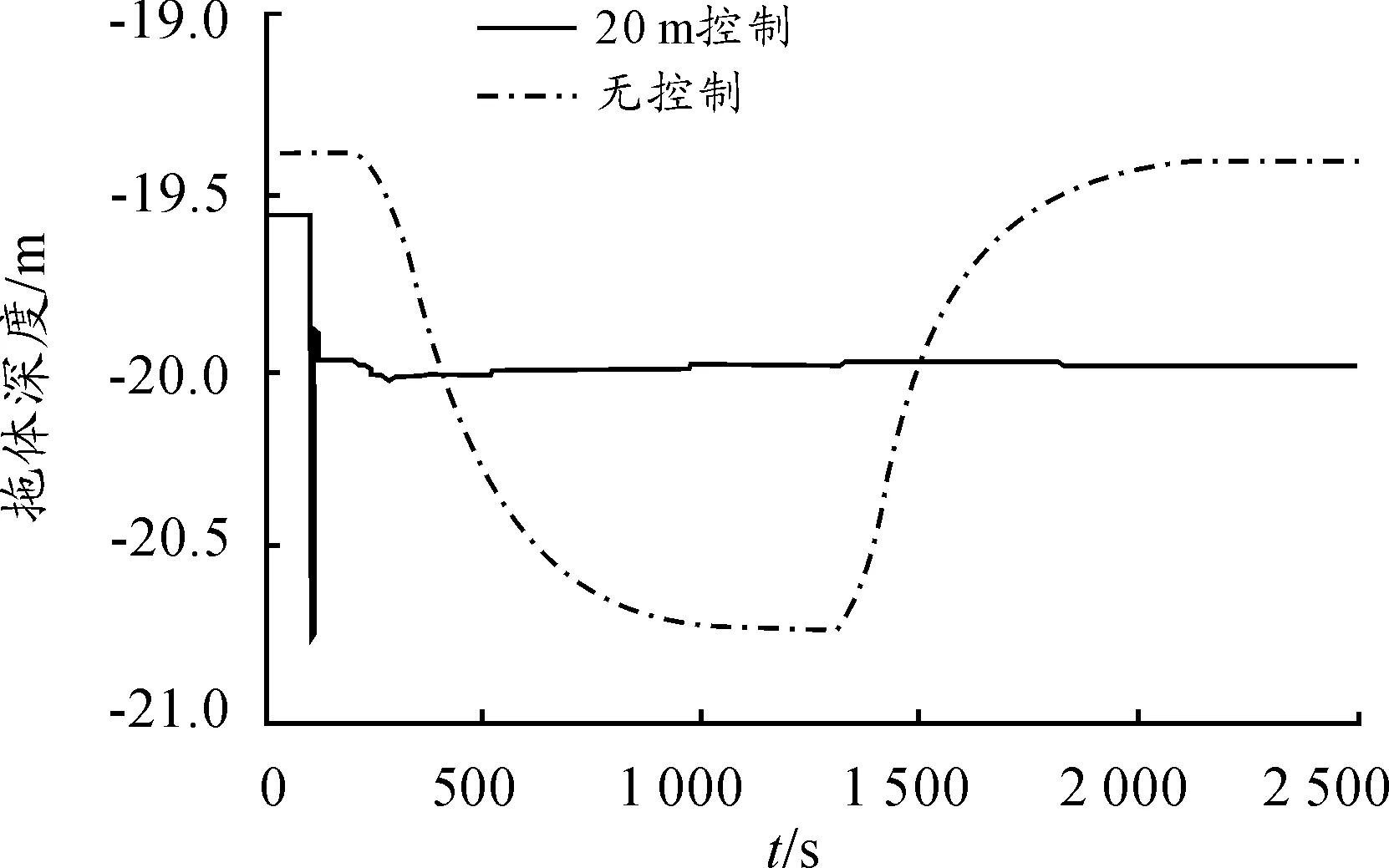
图8　拖体深度变化

图9所示为回转过程中控制水翼不工作和工作状态下拖体的三维轨迹。仿真结果表明，控制水翼工作时(PID参数Kp=0.18，Ki=18，Kd=0.02)，可以大幅度减小因为舰船回转运动过程引起的拖体深度变化。在回转运动过程中，控制水翼不工作时，拖体深度变化范围为5.3 m；而控制水翼工作时，此变化范围仅为0.03 m。因此，通过控制拖体水翼的攻角能有效地削弱舰船回转运动对拖体深度的影响，使拖体在目标深度稳定地工作。

4结论

本文在拖缆和拖体数学模型基础上，耦合了舰船的数学模型，建立了通过改变拖体水翼攻角进行定深的拖曳系统数学模型。分析了舰船机动过程对拖体深度的影响；对比了不同拖曳速度下，拖曳系统的稳定状态和拖体稳定深度；研究了在加速与回转运动过程中控制水翼不工作和工作时拖体深度的变化过程；实现了拖体在不同拖曳速度、加速运动、回转运动三种情况下的目标深度定深功能。数值仿真结果表明，通过改变拖体控制水翼攻角以实现舰船机动中拖曳系统定深这一方法的正确性和有效性，具有一定的理论意义和工程应用价值。

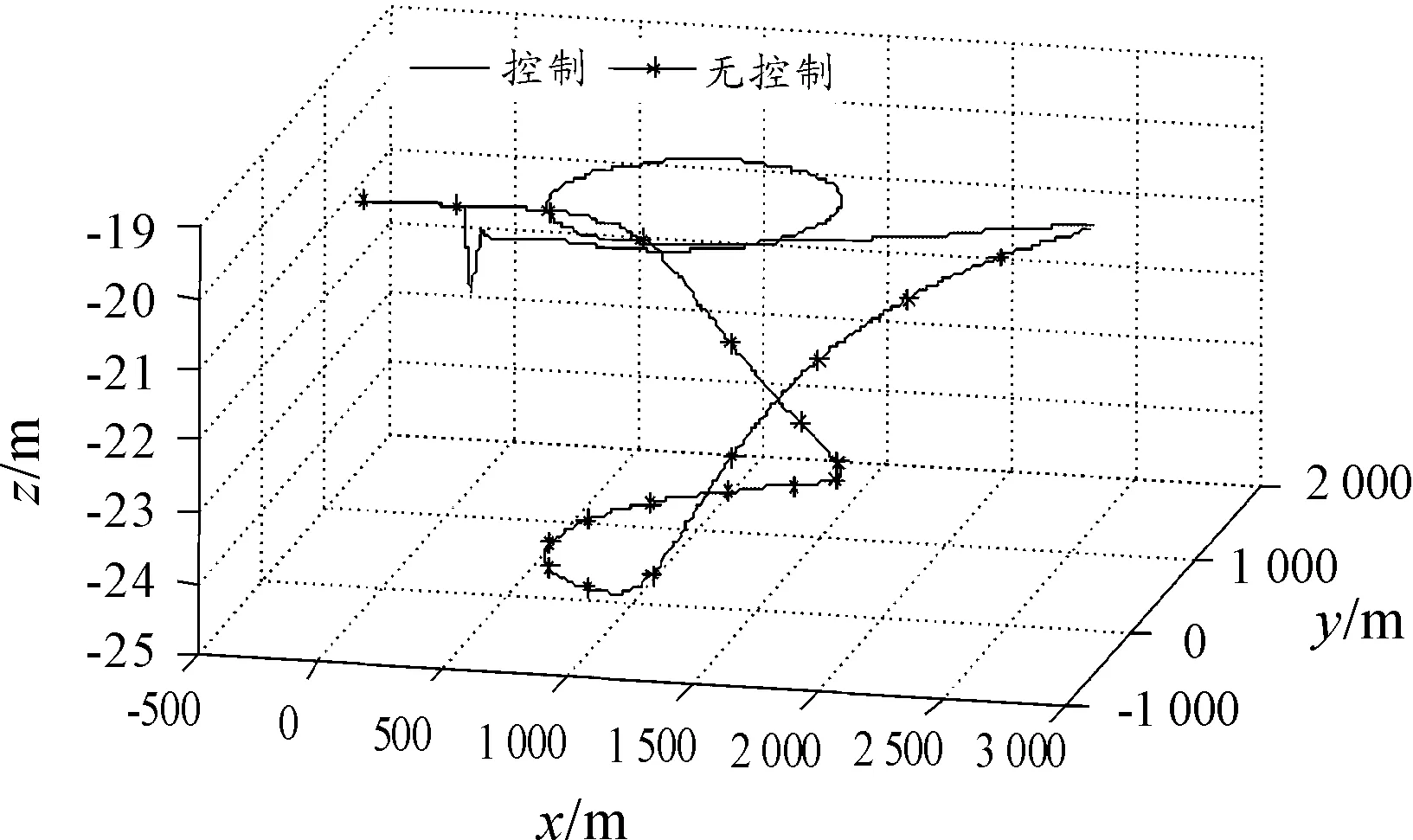
图9　拖体三维轨迹

参考文献：

[1]CHAPMAN D A.Towed Cable Behavior During Ship Turning Maneuvers[J].Ocean Engineering,1984,11(4):327-361.

[2]邓德衡,黄国,楼连根.拖曳线列阵阵形与姿态数值计算[J].海洋工程,1999,17(1):17-26.

[3]王海波,王庆丰.水下拖曳升沉补偿系统的非参数模型自适应控制[J].控制理论与应用,2010,27(4):513-516.

[4]朱军,黄若波,胡忠平.拖曳系统对舰船操纵性影响计算[J].船海工程,2002,145(2):5-10.

[5]李英辉,李喜斌,戴杰,等.拖曳系统计算中拖缆与拖体的耦合计算[J].海洋工程,2002,20(4):37-42.

[6]李志印,吴家鸣.水下拖曳系统水动力特性的计算流体力学分析[J].中国造船,2007,48(2):9-19.

[7]范尚雍.船舶操纵性[M].北京:国防工业出版社,1988.

[8]ABLOW C M,SCHECHTER S.Numerical simulation of undersea cable dynamics[J].Ocean Engineering,1983,10(6):443-457.

[9]施生达.潜艇操纵性[M].北京:国防工业出版社,1995.

[10]WU J M,ALLEN T.Chwang.Investigation on a two-part underwater manoeuvrable towed system[J].Ocean Engineering,2001,28:1079-1096.

(责任编辑杨继森)

本文引用格式：郑智林，苑志江，金良安，等.舰船机动中拖曳系统建模与定深控制研究[J].兵器装备工程学报，2016(4):106-110.

Citation format:ZHENG Zhi-lin, YUAN Zhi-jiang, JIN Liang-an, et al.Mathematic Model and Depth Control of Special Underwater Towed System During Warship Maneuvers[J].Journal of Ordnance Equipment Engineering,2016(4):106-110.

Mathematic Model and Depth Control of Special Underwater Towed System During Warship Maneuvers

ZHENG Zhi-lin, YUAN Zhi-jiang, JIN Liang-an, XIE Tian-hua

(Department of Navigation, Dalian Naval Academy, Dalian 116018, China)

Abstract:The depth of underwater towed system varies during the warship turning maneuvers. Moreover, on the basis of considering the nonlinear interaction relationship between the warship and underwater towed system, the corresponding coupling mathematical model was established. The classical MMG model was adopted by ships and warships, and the finite difference method and 6 DOFs of underwater vehicle were adopted by towing cable and towed vehicle respectively. Using numerical calculation method, the response in the process of system in ship maneuvering was obtained. Using the classical PID algorithm, target depth control of towed body in the process of ship maneuvering was implemented by controlling the body water wing attack angle. Simulation results show the correctness and effectiveness of this method, which has certain theoretical significance and engineering application value.

Key words:underwater towed system; warship turning maneuver; depth control; numerical simulation

文章编号：1006-0707(2016)04-0106-05

中图分类号：P752；TJ8

文献标识码：A

doi:10.11809/scbgxb2016.04.026

作者简介：郑智林(1990—)，男，硕士研究生,主要从事军事航海安全保障与防护技术研究。

收稿日期：2015-10-13；修回日期：2015-11-15

【信息科学与控制工程】