基于三维造型的复杂形状零部件质心位置测量

倪庆乐，王雨时，闻　泉，蔡泓杰，李作华

(1.南京理工大学机械工程学院，南京　210094； 2.辽宁华兴机电有限公司，辽宁 锦州　121017)



基于三维造型的复杂形状零部件质心位置测量

倪庆乐1，王雨时1，闻泉1，蔡泓杰1，李作华2

(1.南京理工大学机械工程学院，南京210094； 2.辽宁华兴机电有限公司，辽宁 锦州121017)

摘要：针对微小型复杂形状零部件质心位置难以测量的问题，采用计算机辅助三维造型技术，通过对零件尺寸的变换，提出了极限质心位置和平均质心位置的测量方法。该方法可极大地降低质心位置测量成本。但该方法未考虑形位误差的影响。经简单算例验算，该方法所得结果与理论计算结果一致。

关键词：测量；三维造型；力学参数；质心位置

引信是精密复杂结构的组合体。为了完成特定功能，引信中有些零件的几何外形被设计成较为复杂的非回转体。这样的非回转体类零件在旋转弹丸引信中，其质心相对于弹丸旋转轴线偏离，会产生较大的离心惯性力，进而因侧壁约束而产生轴向摩擦力，最终会影响引信解除保险和触发等预定功能，甚至引起弹道炸。理论计算很难准确得出这样的复杂几何体的质心位置，而针对引信微小零件质心位置的精密测量仪器目前还未见到。基于三维造型的质心计算机辅助测量方法能够解决此问题，由此获得的质心位置数据可为引信设计和引信动态特性分析提供参考。

文献[1]中应用三点法、四点法测量了水雷的质心，通过原理分析及不确定度评定，表明偏心距测量不确定度小于直径的0.3%，轴向质心位置测量不确定度小于总长的0.1%。文献[2]中对四点法测试弹丸质量、质心(包括偏心距)的原理进行了介绍，基于此原理设计出的试验台可对一般中大口径弹丸进行测量，其轴向质心位置测量误差小于0.2 mm，偏心距测量误差小于0.05 mm。文献[3]中提出了提高弹丸质心位置测量精度的改进方法，其轴向质心位置测量误差小于0.1 mm，而偏心距测量误差小于0.05 mm。文献[4]中概述了复杂回转体零件质心简易测量装置设计，通过改变工装中支块的支撑面形状可满足众多复杂回转体产品的质心测量需求。文献[5]中基于三点法测试原理，设计了一款测试弹丸质心位置的仪器，该仪器的轴向质心位置测量误差小于0.1 mm，偏心距测量误差小于0.01 mm。文献[6]中应用双丝张紧式扭摆测量了回转体的质量偏心，由于该装置不需要称重，所以避免了称重带来的测量误差，它能解决37 mm口径以下弹丸偏心距测量误差较大的问题。文献[7]中提出了适应于发动机批生产过程中质心测量特点的测量方法，并建立了基于计算机测控技术的测试系统。该系统轴向质心测量误差为0.7 mm，径向质心测量误差为0.4 mm。文献[8]中基于三点支撑平台反力原理，提出了一种测量复杂机械产品质心的方法，分析了质心测量系统的误差来源，得出系统的误差主要取决于测力传感器的测量误差和升降推杆的位移误差。文献[9]中使用一种静态平台测量了拖拉机的质心高度，经100次测量得出质心位置测量误差在3 mm以内。文献[10]中采用平台侧倾试验法测量拖拉机质心高度，将拖拉机放在摆动平台上，依靠平台侧面的钢丝滑轮机构，使平台与拖拉机一起旋转一定角度，测量钢丝绳的拉力，通过静态平衡原理计算出拖拉机的质心高度。目前已发表的文献主要是对于回转体弹丸质量偏心的测量方法以及测试仪器的介绍，尚未见有文献涉及微小型复杂非回转体类零件质心位置的测量问题。

本文针对微小型复杂形状零部件质心位置的测量问题，采用计算机辅助三维造型技术，通过对零件尺寸的变换，得出零部件的极限质心位置。

1基于三维造型的复杂形状零件极限质心位置解算

SOLIDWORKS软件可以依据设计图纸很方便地进行三维建模，通过其质量属性功能可以快速查看零件的质心位置。在假设零件材质密度均匀一致的前提下，依据此原理，通过改变零件各尺寸，即可求得零件的极限质心位置。

以某引信活机体零件为例说明此求解过程。

活机体零件各尺寸如图1所示，根据设计图纸，以该零件的平均尺寸建模，在不考虑形位误差的前提下建立三维模型如图2所示。查阅相关文献输入材料密度，通过模型质量与实际零件质量的比较可以确定建模是否正确。活机体零件样品测量质量为25.2 g，三维模型在平均尺寸下质量为27.6 g，误差为8.7%，可认为建模正确。

通过查看质量属性可知，平均尺寸下零件质心偏离外圆柱面轮廓轴线0.955 mm。再考虑其尺寸公差，通过取各尺寸的极大值和极小值来求取零件的极限质心位置数值：

1) 过活机体零件质心O′作垂直于其外圆柱面轮廓轴线的垂直平面。设该平面与外圆柱面轮廓轴线的交点为O。再过O′做OO′的垂面。该垂面将零件分为左右两部分，如图2所示。

2) 分析活机体结构和尺寸，将能使右侧质量增大或左侧质量减小的归于一类，反之归于另一类。

3) 对于不能直接判断其变化如何影响质心位置的某一尺寸可采取如下方法判断：只改变该尺寸，查看质心位置的数值变化，依此来判断其对质心位置的影响。

依次调整可使质心位置数值增大的各尺寸，可得具有最大质心位置(偏心距)的极限尺寸三维模型；同样，也可得具有最小质心位置(偏心距)的极限尺寸三维模型。由此得零件的最大质心位置(偏心距)为1.036 mm，最小质心位置(偏心距)为0.857 mm。

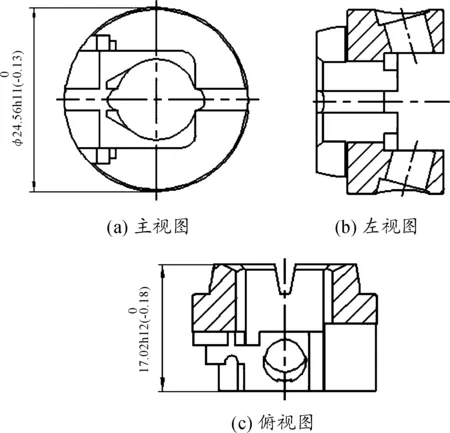
图1　活机体零件结构和尺寸

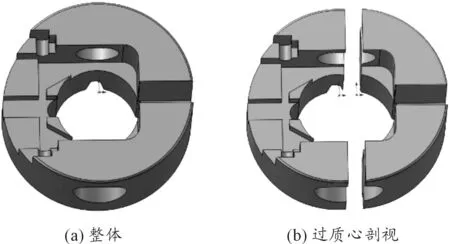
图2　以平均尺寸建立的活机体三维模型

2基于三维造型的部件极限质心位置解算

通过SOLIDWORKS装配功能，将各零件依据相应的约束关系(包括同轴等)装配，可在质量属性中查看装配体的质心位置坐标。依此原理，可分别建立各零件的最大质心位置模型和最小质心位置模型。

以某引信活机体部件为例说明上述求解过程。

该部件包括活机体、锁片、锁片轴、离心子、离心子簧、离心子盖。装配体三维模型如图3所示。

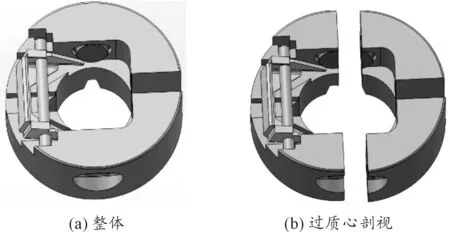
图3　装配体三维模型

装配体各零件的组合方法：

1) 按与上述类似的方法将部件分为左、右两部分，如图3所示。

2) 将能使右侧质量增大或左侧质量减小的零件模型归于一类，反之归于另一类。

3) 对于不能直接判断是取最大质心位置模型或最小质心位置模型的零部件可采取如下方法判断：分别取该零件的最大质心位置模型或最小质心位置模型，查看部件质心位置的变化，依此来判断其对质心位置的影响。

各零件的最大质心位置和最小质心位置如表1所列。

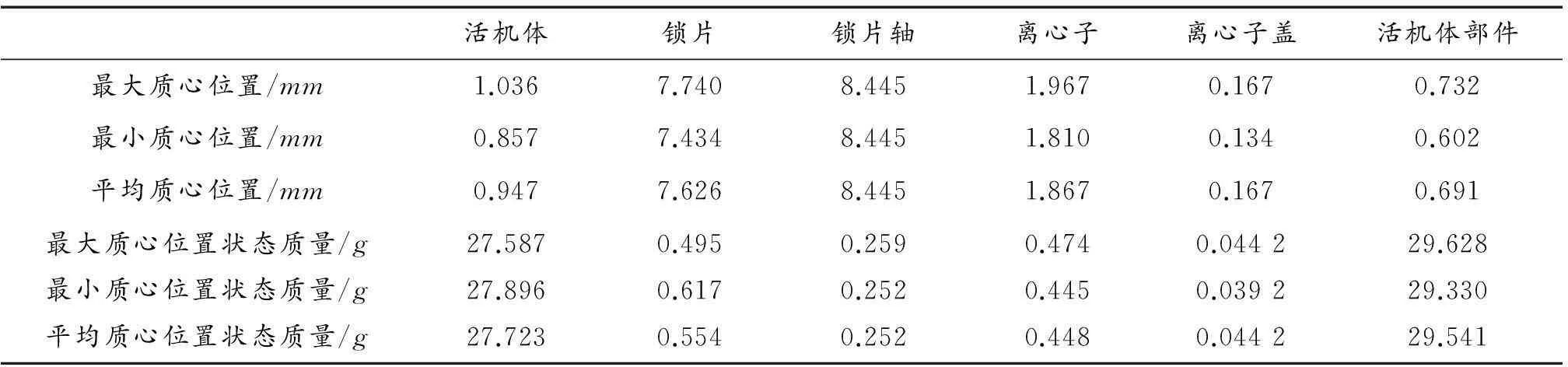
表1　部件中各零件的极限质量偏心值

3方法可信性验算

以一简单零件为例验证此方法的可信性。该零件结构和尺寸如图4所示。

图4　验算用简单零件结构和尺寸

设该零件大圆柱半径为R，高为L；上方小圆柱孔半径为r1，高为l1，其中心线与大圆柱中心线距离为x1；下方圆柱孔半径为r2，高为l2，其中心线与大圆柱中心线距离为x2。则该零件平均质心位置(偏心距)的理论值为

(1)

最大质心位置(偏心距)为

(2)

最小质心位置(偏心距)为

(3)

其中：Xv为质心位置(偏心距)的平均值；Xmax为质心位置(偏心距)的最大值；Xmin为质心位置(偏心距)的最小值；其余符号有类似定义，所有尺寸单位为mm。

按前述方法经三维建模得平均质心位置(偏心距)为0.502mm，最大质心位置(偏心距)为0.529mm，最小质心位置(偏心距)为0.473mm，与理论计算值一致。

4结束语

本文针对微小型复杂形状零部件质心位置的测量问题，采用计算机辅助三维造型技术，通过对零件尺寸的变换，得出零部件的极限质心位置。该方法可极大地降低质心位置测量成本。但该方法未能考虑由于零件形位公差引起的质量偏心。

参考文献：

[1]郑宾，侯文，杨瑞峰.大尺寸柱状结构质量质心测量方法[J].测试技术学报，2002，16(2)：108-111.

[2]顾强，张亚，孙运强.弹体的质量质心及质量偏心测试系统[J].弹箭与制导学报，2003，23(3)：36-38.

[3]骞永博，吴斌.弹丸质量质心测量方法研究[J].弹箭与制导学报，2006，26(3)：126-128.

[4]张可强.复杂回转体零件简易质心测量装置的设计[J].机械工程师，2008(12)：157-159.

[5]姚国年，卫军胡，赵希林，等.高精度弹丸质量偏心测试系统及其误差分析[J].仪器仪表学报，2009，30(4)：862-866.

[6]陈贤隆，丁彩云.用扭摆法测量弹丸的偏心距[J].兵工学报，1993(1)：70-72.

[7]王超.测控技术在固体火箭发动机质心测量中的应用[M].西安：西安电子科技大学，2010.

[8]钟江，赵章风，乔欣，等.基于三点支撑的质心测量系统及误差分析[J].中国机械工程，2010，21(12)：1469-1476.

[9]FABBRIA,MOLARIG.StaticMeasurementoftheCentreofGravityHeightonNarrow-trackAgriculturalTractors[J].BiosystemsEngineering,2004,87(3):299-304.

[10]MOLARIG,RONDELLIV.OntheDefinitionofNarrow-trackWheeledAgriculturalTractors[J].BiosystemsEngineering,2004,88(1):75-80.

(责任编辑唐定国)

本文引用格式：倪庆乐，王雨时，闻泉，等.基于三维造型的复杂形状零部件质心位置测量[J].兵器装备工程学报，2016(4):66-68.

Citation format:NI Qing-le，WANG Yu-shi，WEN Quan,et al.Measurement of Centroid Position for Parts with Complex Shape Based on Three-Dimensional Modeling Techniques[J].Journal of Ordnance Equipment Engineering,2016(4):66-68.

Measurement of Centroid Position for Parts with Complex Shape Based on Three-Dimensional Modeling Techniques

NI Qing-le1，WANG Yu-shi1，WEN Quan1，CAI Hong-jie1，LI Zuo-hua2

(1.School of Mechanical Engineering, Nanjing University of Science & Technology, Nanjing 210094, China；2. Liaoning Huaxing Electromechanical Co., Ltd., Jinzhou 121017, China)

Abstract:Centroid position of micro and small parts with complex shape is difficult to measure, and limit and average centroid positions were got by using computer-aided three-dimensional modeling technology and the converting of part sizes. This method can greatly reduce the costs of measuring centroid position. But this approach fails in considering the influence of geometric error. After checking simple example, the result is consistent with the theoretical value.

Key words:measurement; three-dimensional modeling; mechanical parameter; centroid position

文章编号：1006-0707(2016)04-0066-03

中图分类号：TJ4;TH12

文献标识码：A

doi:10.11809/scbgxb2016.04.017

作者简介：倪庆乐(1991—)，男，硕士研究生，主要从事引信设计及其动态特性研究。

收稿日期：2015-11-13；修回日期：2015-12-05

【机械制造与检测技术】