基于TRMM 3B43数据的川西高原月降水量空间降尺度模拟*

郑　杰，闾　利，冯文兰，涂　坤（成都信息工程大学资源环境学院，成都 610225）



基于TRMM 3B43数据的川西高原月降水量空间降尺度模拟*

郑杰，闾利，冯文兰**，涂坤
（成都信息工程大学资源环境学院，成都 610225）

摘要：利用2001-2013年TRMM 3B43、MODIS-NDVI、DEM、气象观测等数据，在分析植被对降水响应滞后性的基础上，构建了TRMM 3B43数据中月降水量与经纬度、海拔、坡向和NDVI因子间的多元线性回归方程式，作为川西高原月降水量资料的降尺度计算模型，采用“回归方程+残差”的插值方法获取研究区2001-2013年1km空间分辨率的月降水量空间数据，并利用区内16个气象站点的观测数据与模拟结果进行了相关分析和误差检验。结果表明：（1）各气象观测站点基于TRMM 3B43资料的降尺度模拟降水量的数据均具有很高的精度，其中，精度最高的稻城站模拟结果与站点观测值的相关系数高达0.9839，精度最低的小金站相关系数亦高达0.8781；（2）在月、年尺度上，降尺度模拟降水量的数据亦具有很高的精度，其中，5-10月的精度明显高于其它月份，湿润年份精度总体高于干旱年份；（3）降尺度模拟降水量与站点实测降水量整体上相关系数为0.9499，偏差为0.0866，两者吻合度较高，但降尺度模拟降水量值略偏高；（4）降尺度在月尺度上能基本保证TRMM 3B43原始数据的精度，而在年尺度上能有效提高原始数据的精度，加之对空间分辨率的提高，可为获得更加全面、精细的降水分布数据提供有效方法。

关键词：TRMM3B43数据；降水数据；空间降尺度；滞后性；多元线性回归

郑杰,闾利,冯文兰,等.基于TRMM 3B43数据的川西高原月降水量空间降尺度模拟[J].中国农业气象,2016,37(2):245-254

降水是全球水循环的基本组成物质，具有显著的时空变异性，影响一个区域的水分和热量分布，因此，获取精确度较高的降水数据对了解降水量的时空变化特征和掌握区域能量平衡起着重要作用[1-3]。

传统的降水资料主要由地面气象站直接观测获取，并通过实测点插值计算出研究区的空间降水数据，然而，站点观测数据仅能反映站点周边一定范围内地区的降水量，很难有效反映整个区域的空间降水信息[4]。近年来，随着RS和GIS技术的快速发展，通过卫星遥感数据对降水进行探测、反演，覆盖范围广、空间分辨率较高且受气候和地形限制较小的卫星降水观测数据得以实现[5-6]。热带降水测量卫星（Tropical Rainfall Measuring Mission，TRMM）于1997年成功发射，是由美国宇航局（NASA）和日本国家空间发展局（JAXA）共同研制的第一颗专门用于定量测量热带和亚热带地区降水的气象卫星，由于融合了多个卫星的数据以及地面观测数据，该数据空间分辨率和数据质量均较高，且能保证降水数据的均一性[7-8]。然而，尽管TRMM降水数据的空间分辨率在同类卫星降水数据中最高，但仍难以满足流域的水文和气候模型等研究对较高空间分辨率降水数据的需求，因此，进一步提高TRMM数据的空间分辨率及其精度非常必要。

目前，国内外已有学者开展了气象观测站点数据的多元回归统计插值研究以及TRMM 3B43数据的空间降尺度研究。周锁铨等[9]表明，可用多元线性回归方程表示降水量和高程、坡度、坡向等地形信息之间的关系，并在此基础上建立了降水量和地形因子关系的模型，获取了长江中上游地区4km分辨率的空间降水信息；马金辉等[10]通过建立高程、坡度、坡向等地形因子和TRMM降水之间的多元线性回归方程，将TRMM 3B43数据的空间分辨率由原来的0.25°提高至1km。然而，降水是一个复杂的天气过程，且近年来，人类活动对地表过程的影响显著，影响气候的不确定因素增多[11]。植被是连结气候和人文因素的重要纽带[12]，因而，Jia等[13-15]将降水量与归一化植被指数（NDVI）的相关性引入降水数据的空间插值以及降尺度研究中，既不完全依赖于地形因子与降水数据的相关性，又对降水数据的空间变异信息进行了补充，可减小空间插值和降尺度的误差。嵇涛等[16]综合考虑了地形和植被因子，分别从不同空间尺度（0.25°、0.5°、0.75°和1°）对TRMM 3B43数据进行回归模拟，结果指出，川渝地区0.25°分辨率下降水数据的空间降尺度效果最好，且能进一步提高降水估算的精度。然而，目前已有的成果多针对TRMM 3B43的年降水数据进行空间降尺度研究，对月尺度降水数据的空间降尺度研究相对较少。

川西高原地区是长江上游重要的生态屏障，是地理、气象学者研究的重点区域。鉴于该区域气象站点稀少且分布不均匀，本研究充分借鉴已有研究成果的思路，进一步考虑植被生长对降水响应的滞后性特征，结合地形和植被因子构建TRMM 3B43降水数据与经纬度、高程、坡向和NDVI的多元线性回归模型，开展TRMM 3B43月降水数据在地形复杂地区的空间降尺度研究，以期为地形复杂的山区获取高时空分辨率的降水数据提供有效方法。

1　资料与方法

1.1研究区概况

川西高原地区（97 °26′-104°27′E，27°57′-34°21′N）处于横断山脉东段，青藏高原的东部边缘，包括甘孜藏族自治州和阿坝藏族羌族自治州，面积约20万km2。平均海拔3900m，地势高差悬殊，是四川省海拔最高的地区，总体上呈现西部高东部低的态势（图1a）。

川西高原属高山高原高寒气候区，以寒温带气候为主，全区气候垂直变化显著，从河谷到山脊依次可分为亚热带、暖温带、中温带、寒温带、亚寒带、寒带和永冻带。区内气候特征的水平差异也很显著，河谷干暖，山地冷湿。全区冬寒夏凉，太阳辐射强烈，光能资源丰富，年均温4～12℃，极端最低气温-20℃以下，年降水量500～900mm，多集中在5-10月[17]。研究区地形地貌复杂，山脉纵横，地形起伏大（图1b），坡向等地形因子对植被覆盖和降水等的空间分布有较大影响。

图1　研究区高程和气象站点分布(a)及坡向(b)Fig. 1　Elevation and distribution of meteorological stations(a),aspect(b) in study area

1.2数据来源及预处理

研究使用的TRMM 3B43数据为TRMM第6版3级产品（V6-3B43）的月降水资料（http://precip. gsfc.nasa.gov/），空间分辨率为0.25°×0.25°，时间分辨率为1个月。利用IDL程序读取HDF格式的2001-2013年的TRMM 3B43数据，并将其转化为矢量格式的点数据。

MODIS NDVI数据来源于NASA Terra卫星提供的MODIS 13A2 级产品中16d最大值合成NDVI数据集（http://www.gscloud.cn/），数据空间分辨率为1km×1km，时间覆盖范围为2001年1月-2014年1月，该数据在制备过程中经过辐射校正、大气校正、几何校正等预处理。为反映植被变化对降水的响应，对该数据进行投影转换和拼接等处理，并采用最大值合成法（MVC）获取月NDVI值。

SRTM-DEM数据来源于地理空间数据云平台（http://www.gscloud.cn/），该数据由美国宇航局（NASA）和国防部国家测绘局（NIMA）联合测量，空间分辨率为90m×90m。经检查，研究区内没有数据空洞。为建立地形因子与降水的相关关系，首先对DEM数据进行投影转换和裁剪，再采用最临近插值法将其重采样至空间分辨率为1km×1km。

气象资料来源于中国地面气候资料月值数据集（http://cdc.nmic.cn/home.do），包括甘孜藏族自治州和阿坝藏族羌族自治州境内的16个气象站点（图1a）2001-2013年的月降水量数据。为检验研究结果的精度，利用ArcGIS软件生成气象站点降水量的矢量点图层。

1.3研究方法

1.3.1植被对降水的滞后性分析

为了说明植被NDVI因子在降尺度模型构建中的可行性，本文引入植被NDVI的局部Moran’s I指数，该指数用来反映NDVI分布的空间自相关性，即揭示当前像元与其邻近的空间像元NDVI值的相似性，其计算式为

式中，Ii为局部Moran’s I指数，xi和xj分别为空间像元i和j的NDVI值，wij为权重矩阵，n为像元总数；若Moran’s I指数负值太大，说明植被NDVI会影响降尺度模型的精度，需排除这些点的NDVI值。本文运用OpenGeoDa软件计算局部Moran’s I指数。

植被生长受降水的影响较大，本文在降尺度模型中考虑了植被因子，但降水从到地表被植被吸收并反映到植被的生长状况需要一定的时间[18]，即当前月份的植被NDVI值与当月降水的关系并不很密切，在当月降水量降尺度模型中选择当月NDVI值作为植被因子其模拟效果并不理想，因此，本研究通过对比当月、前一月和前两月降水变化与植被NDVI的相关关系，揭示植被NDVI对降水响应的滞后性。

1.3.2降水数据的空间统计降尺度方法

1.3.2.1降尺度原理

统计降尺度方法是指采用统计经验方法确立不同空间尺度影像之间某一特征量的线性和非线性函数关系，从而针对栅格影像进行空间尺度的转换，是低分辨率气候资料转换为高分辨率气候资料的重要手段之一[19]。本文在统计降尺度方法的基础上，结合经纬度、高程、坡向和植被因子，构建适于该地区的TRMM月降水量多元线性回归模型，然后加上回归预测的残差值，得到降尺度后的降水空间分布数据，其模型为

P= F(X,Y,H,V,A)+D TRMMHR（2）

式中，F(X，Y，H，V，A)表示由地形和地理因子线性回归得到的降水预测值，X为经度（º），Y为纬度（º），H为高程（m），V为植被因子，A为坡向因子，ΔTRMMHR为由地形、地理和植被因子引起的降水分布的残差（mm）。马金辉等[10]在建立降水量与地形因子之间的回归方程时，采用坡向的余弦值来计算降水量，取得了较理想的结果，因此，本文在月降水量降尺度模型的建立时也采用坡向的余弦值来量化坡向因子。

1.3.2.2降尺度步骤

（1）对研究区边界向外做25km的缓冲区（约向外增加一个TRMM像元），以缓冲区边界裁取研究区内2001-2013年TRMM 3B43月降水量格点数据。

（2）在0.25°分辨率下提取每一个对应位置上TRMM像元的逐月降水量值，以及该点对应的经纬度信息（X、Y）、海拔值（H）、坡向的余弦值（A）、植被因子的值（V），构建多元线性回归模型F（X，Y，H，V，A）0.25°。

（3）在0.25°分辨率下，计算模拟预测值与TRMM原始降水量数据的残差ΔTRMMLR，并运用样条函数法插值到1km空间分辨率残差影像，即

ΔTRMMLR= TRMM3B43-F(X,Y,H,V,A)0.25o（3）

（4）将1km分辨率的经纬度、DEM、坡向因子和植被因子等影像代入多元线性回归模型F（X，Y，H，V，A）0.25°中计算1km分辨率的预测降水量F（X，Y，H，V，A）。再利用式（2）通过预测降水量数据和残差数据叠加得到1km分辨率的降尺度模拟降水量。

1.3.3模拟结果检验方法

分别计算降尺度模型模拟的降水量数据、TRMM 3B43原始降水量数据与地面站点实测降水量数据的相关系数（R）、偏差（Bias）和均方根误差（RMSE），对两组数据的一致性和误差进行检验分析，计算式为

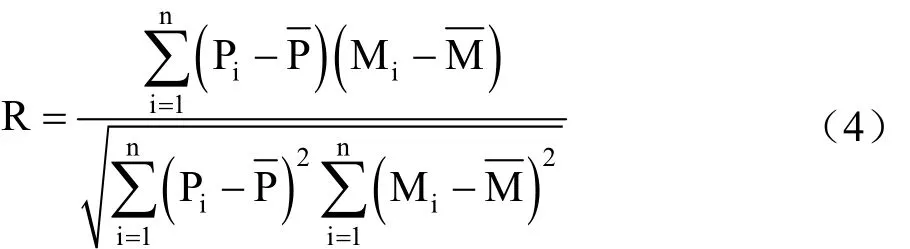
其中

式中，iP和Mi分别表示站点实测降水量和降尺度模拟降水量或TRMM 3B43降水量数据，n为样本容量；相关系数R用来反映两组数据的密切程度，R的取值范围为[0,1]，数值越接近1，表示数据的一致性越好；偏差反映站点实测数据与降尺度模拟数据或TRMM 3B43原始数据的偏离程度，其中Bias>0，说明估算值大于实测值，Bias越接近0，两组数据的吻合度越高，本研究以|Bias|表示相对误差；均方根误差也用来表示降尺度模拟降水量与站点实测降水量之间的偏差，数值越小，表示两组数据误差越小。

2　结果与分析

2.1月降水量降尺度模型的建立

2.1.1植被指数对月降水量响应的时间滞后性

像元NDVI的Moran’s I指数为负，主要是由河流、湖泊和人类活动干扰等因素造成的，NDVI值的空间变异性较大，会影响降尺度模型的构建。考虑到不同地物NDVI的大小有所差异，本研究将Moran’s I指数<-1的区域认为是水体的干扰。计算研究区多年年最大NDVI的Moran’s I指数发现，研究区平均Moran’s I指数为0.17，其中，65%像元的NDVI值的Moran’s I指数>0，Moran’s I指数<-1（空间变异较大）的仅占0.04%，综合考虑Moran’s I指数，故引入植被NDVI作为因子之一进行TRMM 3B43数据的降尺度研究是可行的。同时，为了排除水体NDVI值对降尺度模型精度的影响，本研究在构建降尺度模型时，未将水体的NDVI值参与方程的构建。

川西高原逐月NDVI与当月、前一月和前两月降水量的相关系数见表1。由表可见，（1）从年内的对比来看，多数月份的月NDVI值与前一月降水量有更高的相关系数，尤其在4、5、6和10月，两者相关性均通过显著性检验；（2）无论是在植被生长期（5-10月）还是全年平均，植被月NDVI与前一月降水量的相关系数（R前一月）>当月（R当月）>前两月（R前两月）。综上可知，研究区植被对降水的响应具有一定的滞后性，整体来看滞后期约为1个月，这与相关研究成果一致[20-21]。因此，本研究选取下一个月的植被NDVI值作为当月降水的降尺度模型的植被因子。

表 1　川西高原逐月NDVI与当月、前一月及前两月降水量的相关系数Table 1　Correlation coefficients between NDVI of current month and precipitation of current month, previous month, month before previous one in the Western Sichuan Plateau

2.1.2月降水量数据的降尺度模型

考虑到川西高原地区植被对降水响应的滞后性，同时考虑山区存在最大或最小降水高程带[22]，将式（2）展开为一次多项式，并进一步对高程和NDVI进行三次多项式的展开，得到最终的降尺度模型为

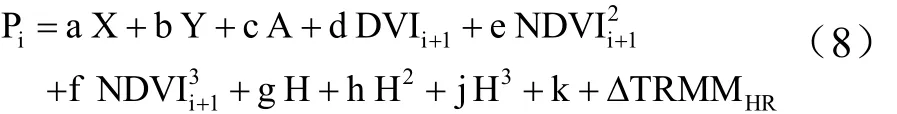
式中，Pi为第i月的降尺度模拟降水量(mm)；X为经度(°)；Y为纬度(°)；A为坡向的余弦值；NDVIi+1为第i+1月的NDVI值，当i=12时，NDVIi+1为下一年1月的NDVI值；H为海拔(m)；ΔTRMMHR为1km空间分辨率的残差影像；a，b，c，d，…，j，k为多元线性回归模型的回归系数。

2.2月降水量降尺度模型的有效性检验

2.2.1各站点精度检验

将2001-2013年16个气象观测站的月降水量，与各站点对应地理位置的降尺度模型模拟的月降水量进行对比，其散点分布和相关系数见图2。由图可见，（1）色达、甘孜、理塘、稻城和九龙站，其模拟值与实测值的相关系数R>0.97（P<0.001），且散点多集中在线性趋势线周边，说明这些气象站点的降尺度模拟结果与实测降水量的相关性显著且偏离程度较小，数据精度高；（2）若尔盖、马尔康和石渠等（图2 f-图2 l）7个站点，其模拟值与实测值的相关系数R在0.95～0.97（P<0.001），散点分布相对较集中，仅少部分点偏离线性趋势线较远，数据精度相对较高；（3）红原、小金、巴塘和康定站点模拟值与实测值的相关系数偏低（R<0.95，P<0.001），其中小金站的相关系数最低，仅0.8781，明显低于研究区其它站点，且其散点分布较分散，有较多的点偏离线性趋势线的程度较高，说明该站点降尺度结果的精度相对偏低。总体上（对比图1a），西部海拔相对较高的甘孜藏族自治州各站的精度相对较高，海拔相对较低的阿坝藏族羌族自治州的精度相对偏低。

以研究区气象站点所在1km范围内的平均高程为自变量，分别以各站点降尺度模型模拟的降水量与实测值之间的相关系数R和相对误差|Bias|为因变量作三次多项式回归分析，高程与R和|Bias|的相关系数分别为0.7409和0.6998，均通过0.05水平的显著性检验，呈现较强的三次函数关系特征。随着海拔的升高，相关系数也随之增加，且增加的速度不断减缓，|Bias|值则随着海拔的升高呈现急剧减小—缓慢增大的波动变化趋势。由图2和图3可见，R值最低的站点，其|Bias|最大，即降尺度模拟数据精度最差的站点是海拔高度最低的小金站，其原因是：（1）由于数据记录的不连续性以及融合地面雨量统计资料时算法本身的不足，导致TRMM 3B43原始降水数据的精度存在一定问题；（2）小金站点地处河谷区，海拔高度2273m，但周围高山脊的海拔高达4500m（图1a），高程落差2000m左右，地形起伏较大，气候垂直变化显著，且岭谷地貌对大气流通的阻隔作用较大，导致该地区降水误差明显[23]。

图2　2001-2013年利用降尺度模型模拟各站点月降水量与实测值的散点图Fig. 2　Scatter diagram of monthly precipitation between simulated by downscaling model and observed during 2001-2013

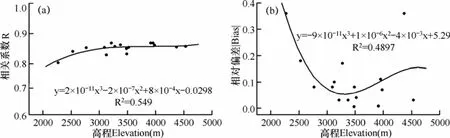
图3　川西高原地区高程与相关系数R（a）、相对偏差|Bias|（b）的散点图Fig.3　Scatter diagram of elevation, R(a) and |Bias|(b) in the Western Sichuan Plateau

2.2.2各月精度检验

分别统计历年降尺度模型模拟的各月降水量和TRMM 3B43数据中各月降水量资料，与16个气象观测站的月降水量进行对比，其相关系数、偏差和均方根误差统计结果见表2。由表可见，（1）各月降尺度模型模拟的降水量与实测站点降水量的相关系数均通过0.001水平的显著性检验，1月和12月的相关系数相对偏低（R<0.6），其余月份两组数据均具有较强的相关性（R>0.7）。其中降水量相对集中的5-10月，降尺度模型模拟的降水量与站点实测数据的偏差较低（Bias<0.1），同时偏差值相对较高的1-4月和11-12月降尺度模拟结果的均方根误差较低，可见，对川西高原地区2001-2013年的TRMM 3B43月降水数据进行降尺度操作取得很好的效果，降尺度模拟结果比站点实测数据略偏高；（2）降尺度模型模拟的各月降水量、TRMM 3B43原始数据各月降水量数据2-10月的R、Bias和RMSE的值基本相近，其中4、5、6和9月降尺度模型模拟的降水量的精度比TRMM 3B43原始数据的精度略偏高；相比而言，1、11和12月降尺度模型模拟的降水量的精度较之TRMM 3B43原始数据明显偏低，说明多数情况下降尺度结果能够保证原始数据的精度，但降水量偏低的情况下降尺度效果不佳，其原因一是降水量偏低的月份，降水量与植被指数的相关性偏低（表1），多元线性回归模型的精度相对偏低，导致降尺度效果不佳；二是降水量偏低的月份，TRMM 3B43原始数据相对于站点实测值的误差也较大，精度较低，导致降尺度模拟数据的精度较低。

2.2.3典型干湿年份精度检验

选取2001-2013年间降水量最多的年份2012年（776.64mm）作为湿润年份，降水量最少的年份2006年（598.27mm）作为干旱年份，将典型干、湿年份的降尺度模型模拟数据和TRMM 3B43数据的各月降水量资料，与16个气象观测站的月降水量进行对比。由表3可见，（1）干湿年份两组数据的相关系数数值接近，且均通过0.001水平的显著性检验，湿润年份降尺度模型模拟的数据的偏差和均方根误差均低于TRMM 3B43原始数据，干旱年份降尺度模型模拟的数据的偏差低于TRMM 3B43原始数据，均方根误差略高于TRMM 3B43原始数据，可见，降尺度模型模拟的数据精度较高。（2）2012年两组数据的均方根误差均略低于2006年，但其相关系数大于2006年，且偏差更接近0，说明湿润年份的降尺度模型模拟的数据精度略高于干旱年份。

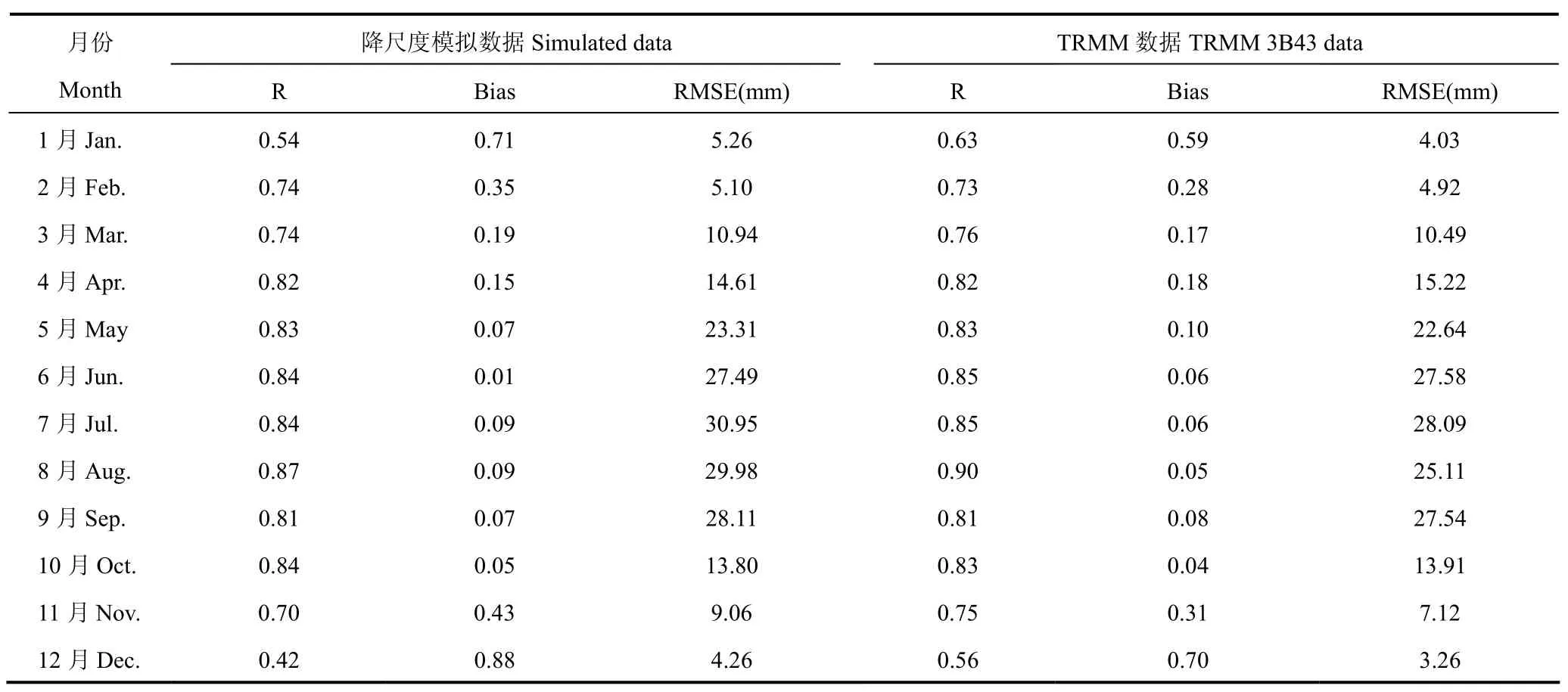
表2　2001-2013年两组数据各月降水量与实测值间的误差统计Table 2　Statistics of error between monthly precipitation of two sets data and observed during 2001-2013

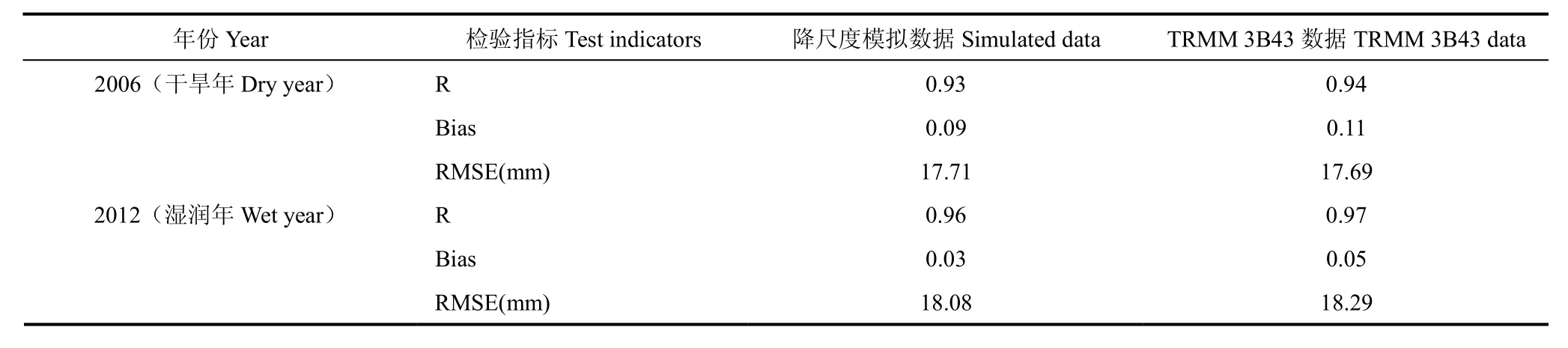
表3　典型年两组数据的检验结果Table 3　Validation results of two sets data in two typical years

2.2.4整体精度检验

将2001-2013年16个气象观测站对应位置、年份和月份的降尺度模型模拟数据和TRMM 3B43数据的各月降水量值分别与站点实测值作一元线性回归分析，其散点分布和误差统计见图4。由图4a可见，（1）降尺度模型模拟的月降水量和站点实测月降水量的相关系数达到0.9499（P<0.001），两者存在显著的线性相关关系；两组数据的偏差为0.0866，表明降尺度模型模拟的月降水量值整体略偏高。（2）对比图4b可见，降尺度模型模拟的月降水量与站点实测月降水量的R值、Bias值、RMSE值虽然比TRMM 3B43原始数据与之相对应的值略偏低，但基本接近，表明降尺度模拟的结果与站点实测数据误差形成的主要原因是TRMM 3B43数据本身存在一定的误差[10]；同时，川西高原地势复杂，地形因素对大气流动的影响很大，而本文在利用TRMM 3B43数据结合经纬度、高程、坡向和NDVI进行多元线性回归分析时，高程和坡向并不能完全代表整个地形因素对降水的影响，导致个别气象观测站点的模拟值误差偏大（图2）。

整体而言，降尺度模型模拟的月降水量的精度较高，虽略低于TRMM 3B43原始数据的精度，但相差不大，说明本文TRMM 3B43数据降尺度的模型是可行的，同时又提高了降水数据的空间分辨率，能够更加全面地反映川西高原地区降水量分布的空间格局。

图 4　2001-2013年降尺度模拟月降水量(a)和TRMM3B43月降水量(b)与实测值间的散点图Fig. 4　Scatter diagram of monthly precipitation between observed and simulated by downscaling model(a) and TRMM 3B43 data(b) during 2001-2013

3　结论与讨论

（1）在空间上，各气象观测站点降尺度模型模拟的降水量数据精度较高，其中，精度最高的稻城站模拟结果与站点实测值的相关系数高达0.9839，精度最低的小金站相关系数亦高达0.8781，且该数据精度的空间差异明显，西部的甘孜藏族自治州的数据精度比东部的阿坝藏族羌族自治州偏高，这主要与TRMM 3B43原始数据自身的精度、研究区复杂的地形地貌以及多元线性回归模型的精度有关。

（2）在月尺度上，降尺度模型模拟的月降水量数据与站点实测数据的吻合度较好，能较好地反映区域降水量的年内变化，但各月份的精度有所差异，降水相对集中的5-10月比其它月份数据精度较高。与TRMM 3B43原始降水数据相比，降尺度模型模拟的月降水量在不降低其数据精度的基础上，大幅提高了数据的空间分辨率，使其能更加全面、精细地反映研究区降水的空间分布特征。

（3）在年尺度上，典型干、湿年份降尺度模型模拟的降水量数据的精度较高，且略高于TRMM 3B43原始数据的精度。同时，湿润年份的精度高于干旱年份，这与在降尺度过程中同样考虑到植被NDVI因子的Immerzeel等[13，16]的研究成果不一致，其原因一是植被的影响，湿润年份与干旱年份相比，降水量更充足，植被对降水响应的滞后性更明显，降水集中的5-10月多元回归模型的效果更好，精度更高；二是TRMM 3B43原始数据的影响，湿润年份TRMM原始数据的精度比干旱年份偏高，与本文降尺度模型模拟结果干湿年份的精度对比结果一致，这也进一步说明了在降尺度过程中考虑植被对降水响应的滞后性，降尺度模型模拟的数据与TRMM原始数据能呈现更好的一致性。

（4）研究区2001-2013年156个月的降尺度模型模拟的月降水量与16个地面观测实测值整体上的R=0.9499，Bias=0.0866，RMSE=19.92，说明降尺度结果与站点实测降水数据之间存在显著的线性相关关系，数据误差较小，数据精度较高，降尺度模型可行。且与TRMM 3B43原始数据的整体精度相比，降尺度模型模拟的数据精度与之非常接近，只是略偏低，说明本文降尺度数据适于川西高原地区的降水研究。但马金辉等[10,24]在对TRMM 3B43年降水量降尺度研究中发现降尺度结果的精度较之原始数据偏高，可能是因为马金辉等是针对TRMM年降水数据进行降尺度研究，而本文是对TRMM月降水数据进行降尺度研究，研究的时间尺度不同，且年内不同月份降水量的降尺度精度有所差异，说明降水量的年内变化是影响年尺度和月尺度降水数据降尺度精度的主要原因。

参考文献References

[1] Goovaerts P.Geostatistical approaches for incorporating elevation into the spatial interpolation of rainfall[J].Journal of Hydrology, 2000,228(1):113-129.

[2] Bohnenstengel S,Schlünzen K,Beyrich F.Representativity of in situ precipitation measurements :a case study for the LITFASS area in North-Eastern Germany[J].Journal of Hydrology,2011,400(3-4):387-395.

[3]曾丽红,宋开山,张柏,等.1960-2008年吉林省降水量的时空演变特征[J].中国农业气象,2010,31(3):344-352.

Zeng L H,Song K S,Zhang B,et al.Spatial-temporal precipitation variation over Jilin Province during 1960-2008[J].Chinese Journal of Agrometeorology,2010,31(3):344-352.(in Chinese)

[4]朱会义,刘述林,贾绍凤.自然地理要素空间插值的几个问题[J].地理研究,2004,23(4):425-432.

Zhu H Y,Liu S L,Jia S F.Problems of the spatial interpolation of physical geographical elements[J].Geographica Research, 2004,23(4):425-432.(in Chinese)

[5]张涛,李宝林,何元庆,等.基于TRMM订正数据的横断山区降水时空分布特征[J].自然资源学报,2015,30(2):261-270.

Zhang T,Li B L,He Y Q,et al.Spatial and temporal distribution of precipitation based on corrected TRMM data in Hengduan Mountains[J].Journal of Natural Resources,2015,30(2):261-270. (in Chinese)

[6]吕洋,杨胜天,蔡明勇,等.TRMM卫星降水数据在雅鲁藏布江流域的适用性分析[J].自然资源学报,2013,28(8):1414-1425.

Lv Y,Yang S T,Cai M Y,et al.The applicability analysis of TRMM precipitation data in the Yarlung Zangbo River Basin[J]. Journal of Natural Resources,2013,28(8):1414-1425.(in Chinese)

[7]曾红伟,李丽娟.澜沧江及周边流域TRMM3B43数据精度检验[J].地理学报,2011,66(7):994-1004.

Zeng H W,Li L J.Accuracy validation of TRMM3B43data in Lancang River Basin[J].Acta Geographica Sinica,2011,66(7): 994-1004.(in Chinese)

[8]朱国锋,蒲焘,张涛,等.TRMM降水数据在横断山区的精度[J].地理科学,2013,33(9):1125-1131.

Zhu G F,Pu T,Zhang T,et al.The accuracy of TRMM precipitation data in Hengduan Mountainous region,China[J]. Scientia Geographica Sinica,2013,33(9):1125-1131.(in Chinese)

[9]周锁铨,薛根元,周丽峰,等.基于GIS降水空间分析的逐步插值方法[J].气象学报,2006,64(1):100-111.

Zhou S Q,Xue G Y,Zhou L F,et al.The stepwise interpolation approach of precipitation for spatial analysis based on GIS[J]. Acta Meteopologica Sinica,2006,64(1):100-111.(in Chinese)

[10]马金辉,屈创,张海筱,等.2001-2010年石羊河流域上游TRMM降水资料的降尺度研究[J].地理科学进展,2013, 32(9):1423-1432.

Ma J H,Qu C,Zhang H X,et al.Spatial downscaling of TRMM precipitation data based on DEM in the upstream of Shiyang River Basin during 2001-2010[J].Progress in Geography,2013,32(9):1423-1432.(in Chinese)

[11]徐成东,孔云峰,仝文伟.线性加权回归模型的高原山地区域降水空间插值研究[J].地球信息科学,2008,10(1):14-19.

Xu C D,Kong Y F,Tong W W.A weighted Linear Regression Model for precipitation spatial interpolation in Altiplano and Mountain in area[J].Geo-information Science,2008,10(1):14-19. (in Chinese)

[12]李晓光,刘华民,王立新,等.鄂尔多斯高原植被覆盖变化及其与气候和人类活动的关系[J].中国农业气象,2014,35(4): 470-476.

Li X G,Liu H M,Wang L X,et al.Vegetation cover change and its relationship between climate and human activities in Ordos Plateau[J].Chinese Journal of Agrometeorology,2014, 35(4):470-476.(in Chinese)

[13]Immerzeel W W,Rutten M M,Droogers P.Spatial downscaling of TRMM precipitation using vegetative response on the Iberian Peninsula[J].Remote Sensing of Environment,2009, 113(2):362-370.

[14]王智,吴友均,梁凤超,等.新疆地区年降水量的空间插值方法研究[J].中国农业气象,2011,32(3):331-337.

Wang Z,Wu Y J,Liang F C,et al.Study on spatial interpolation method of annual precipitation in Xinjiang[J].Chinese Journal of Agrometeorology,2011,32(3):331-337.(in Chinese)

[15]Jia S,Zhu W,Lv A,et al.A statistical spatial downscaling algorithm of TRMM precipitation based on NDVI and DEM in the Qaidam Basin of China[J].Remote Sensing of Environment,2011,115(12):3069-3079.

[16]嵇涛,刘睿,杨华,等.多源遥感数据的降水空间降尺度研究:以川渝地区为例[J].地球信息科学学报,2015,17(1):108-117.

Ji T,Liu R,Yang H,et al.Spatial downscaling of precipitation using multi-source remote sensing data:a case study of Sichuan-Chongqing Region[J].Journal of Geo-information Science,2015,17(1):108-117.(in Chinese)

[17]张虹娇.川西北高原气候变化特征研究[J].西南大学学报（自然科学版）,2014,36(12):148-156.

Zhang H J.A study on the characteristics of climate change on Northwestern Sichuan Plateau[J].Journal of Southwest University(Natural Science Edition),2014,36(12):148-156.(inChinese)

[18]姜琳,冯文兰,郭兵.雅鲁藏布江流域近13年植被覆盖动态监测及与降水因子的相关性分析[J].长江流域资源与环境,2014,23(11):1610-1619.

Jiang L,Feng W L,Guo B.Analysis of dynamic monitoring of vegetation change and the correlation with precipitation factor in Yalu Tsangpo River Basin during the past 13 years[J].Resources and Environment in the Yangtze Basin, 2014,23(11):1610-1619.(in Chinese)

[19] Chen J,Brissette F P,Leconte R.Coupling statistical and dynamical methods for spatial downscaling of precipitation[J]. Climatic Change,2012,114(3-4):509-526.

[20]白建军,白江涛,王磊.2000-2010年陕北地区植被NDVI时空变化及其与区域气候的关系[J].地理科学,2014,34(7): 882-888.

Bai J J,Bai J T,Wang L.Spatio-temporal change of vegetation NDVI and its relation with regional climate in Northern Shaanxi Province in 2000-2010[J].Scientia Geographica Sinica,2014,34(7):882-888.(in Chinese)

[21]白淑英,王莉,史建桥.长江流域NDVI对气候变化响应的时滞效应[J].中国农业气象,2012,33(4):579-586.

Bai S Y,Wang L,Shi J Q.Time lag effect of NDVI response to climatic change in Yangtze River Basin[J].Chinese Journal of Agrometeorology,2012,33(4):579-586.(in Chinese)

[22]王超,赵传燕.TRMM多卫星资料在黑河上游降水时空特征研究中的应用[J].自然资源学报,2013,28(5):862-872.

Wang C,Zhao C Y.A study of the spatio-temporal distribution of precipitation in upper reaches of Heihe River of China using TRMM data[J].Journal of Natural Resources, 2013,28(5):862-872.(in Chinese)

[23]嵇涛,杨华,刘睿,等.TRMM卫星降水数据在川渝地区的适用性分析[J].地理科学进展,2014,33(10):1375-1386.

Ji T,Yang H,Liu R,et al.Applicability analysis of the TRMM precipitation data in the Sichuan-Chongqing region[J].Progress in Geography,2014,33(10):1375-1386.(in Chinese)

[24]李净,张晓.TRMM降水数据的空间降尺度方法研究[J].地理科学,2015,35(9):1164-1169.

Li J,Zhang X.Downscaling method of TRMM satellite precipitation data[J].Scientia Geographica Sinica,2015,35(9): 1164-1169.(in Chinese)

Spatial Downscaling Simulation of Monthly Precipitation Based on TRMM 3B43 Data in the Western Sichuan Plateau

ZHENG Jie, LV Li, FENG Wen-lan, TU Kun
(College of Resources and Environment, Chengdu University of Information Technology, Chengdu 610225, China)

Abstract:Using TRMM 3B43 data, MODIS-NDVI, DEM, meteorological data of observation stations during 2001-2013, a multiple linear regression model was built among TRMM 3B43 monthly precipitation and longitude, latitude, altitude, aspect, NDVI factor as downscaling model of monthly precipitation data in the Western Sichuan Plateau based on the analysis of the lag of vegetation response to precipitation. Then, combined with regression equation and residuals, interpolation method was adopted to obtain monthly precipitation data with 1km spatial resolution. Finally, the accuracy of simulated data obtained by downscaling model was tested by the correlation analysis and error detection between the simulated results and the observation data of 16 meteorological stations in the study area. The results showed as follows: (1) Precipitation simulated by downscaling model based on TRMM 3B43 data had a high precision in all meteorological observation stations. Daocheng site displayed the highest accuracy, the correlation coefficient between simulation results and observed values attained 0.9839, while Xiaojin site displayed the lowest accuracy, the correlation coefficient was 0.8781. (2) The precipitation simulated by downscaling model displayed high accuracy in the whole study area at both monthly and yearly time scale. The accuracy of simulated results from May to October was significantly higher than other months, as well as typical wet year (2012) was higher than dry year (2006). (3) The precipitation simulated by downscaling model displayed high accuracy to the observation data on the whole(R=0.9499, Bias=0.0866), while thevalue of simulated precipitation was slightly higher. (4) Compared to the original data TRMM 3B43, the simulated data by downscaling model guaranteed the accuracy and improved the spatial resolution. So, this method could provide an effective way to produce a more sophisticated precipitation data with higher spatial resolution.

Key words:TRMM 3B43 data; Precipitation data; Spatial downscaling; Lag; Multiple linear regression

doi:10.3969/j.issn.1000-6362.2016.02.015

* 收稿日期：2015-08-11**通讯作者。E-mail：fwl@cuit.edu.cn

基金项目：国家自然科学基金项目（41301653）

作者简介：郑杰（1991-），硕士生，主要从事3S集成与气象应用研究。E-mail：zhengjie0601@sina.com