例谈构建数学模型解决基因频率相关问题

马兰萍++闫芳

所谓数学模型，就是为了某种目的，用字母、数字及其他数学符号建立起来的等式或不等式，以及图表、图象、框图等描述客观事物的特征及其内在联系的数学结构表达式。在生物学科教学中，数学模型对学生理科思维培养和训练能起到一定的作用。

高中生物学科的考查以描述性的语言为主，于是很多学生认为只要记住、理解基础知识就可以了，他们并不善于运用数学工具解决生物学上的一些问题。而在生物《必修2·遗传与进化》中，许多问题的解决需要灵活运用数学知识，如种群是生物进化的基本单位，生物进化的实质是种群基因频率的改变。在近几年的高考中均有对基因频率和基因型频率计算的考查，因此在高考复习中如何帮助学生构建数学模型，用数学方法讨论基因频率和基因型频率的变化，是急需解决的问题。笔者精选了2013年山东高考题中的一道典型试题，探讨数学模型的构建过程。

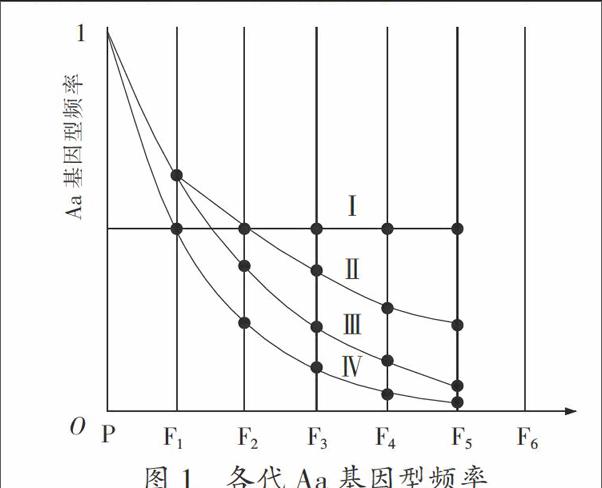
（2013·山东卷）用基因型为Aa的小麦分别进行连续自交、随机交配、连续自交并逐代淘汰隐性个体、随机交配并逐代淘汰隐性个体，根据各代Aa基因型频率绘制曲线如图1，下列分析错误的是（ ）

A. 曲线Ⅱ的F3中Aa基因型频率为0.4

B. 曲线Ⅲ的F2中Aa基因型频率为0.4

C. 曲线Ⅳ的Fn中纯合体的比例比上一代增加（1/2）n+1

D. 曲线Ⅰ和Ⅳ的各子代间A和a的基因频率始终相等

答案：C。

本题为2013年山东理综卷生物选择题的压轴题，考查的是分离定律的应用，涉及到基因频率和基因型频率的计算，难度比较大，对考生获取信息、图文转换、综合分析问题等方面的能力要求较高。因此，在高考复习中，笔者将此题作为典型例题，引导学生仔细分析，推导出相关公式，联系对应曲线，构建起相关的数学模型，从而解决题目中的问题。

首先，四条曲线起点都是1，分别与题干中四种情况存在对应关系，需要教师引导学生先从简单熟悉的情况着手。

曲线Ⅰ从F1代之后Aa的基因型频率稳定在0.5，说明种群处于遗传平衡状态（即种群非常大，雌雄个体自由交配并产生后代，无自然选择，无基因突变，没有迁入迁出），所以曲线Ⅰ对应的是Aa小麦随机交配的情况。

曲线Ⅳ对应的数值变化，符合y=（1/2）n函数曲线，是Aa连续自交后代中杂合子的基因型频率（图2）。

曲线Ⅲ距离曲线Ⅳ比较近，可能是连续自交并逐代淘汰隐性个体后Aa的基因型频率。这种猜测是否正确呢？这需要进行科学分析和计算。已知Aa进行连续自交n代：Aa基因型频率=1/2n，AA基因型频率=aa基因型频率=1/2（1-1/2n）；淘汰隐性个体后，代入数值化简，得到Aa=2/（2n+1）。

曲线Ⅱ可能对应Aa随机交配并逐代淘汰隐性个体的情况。对此，进行推导：

Aa随机交配一代，F1中AA∶Aa∶aa=1∶2∶1，淘汰aa后，AA∶Aa=1∶2，Aa占2/3，曲线Ⅱ与Ⅲ在此处相交于一点。

F1中a基因频率=1/3，A基因频率=2/3，随机交配，F2中AA∶Aa∶aa=4/9∶4/9∶1/9，淘汰aa后，AA=Aa=1/2=2/4。

F2中a基因频率=1/4，A基因频率=3/4，随机交配，F3中AA∶Aa∶aa=9/16∶6/16∶1/16，淘汰aa后，AA∶Aa=3∶2，Aa占2/5。

F3中a基因频率=1/5，A基因频率=4/5，随机交配，F3中AA∶Aa∶aa=16/25∶8/25∶1/25，淘汰aa后，AA∶Aa=2∶1，Aa占1/3=2/6。

……

由此，Aa随机交配n代并逐代淘汰隐性个体后Aa=2/（n+3）

在这道试题的解决过程中，教师引导学生运用逻辑推理、构建出不同题境下的数学表达式，并识别符合特定条件的曲线，提高了解题速度，丰富了学生阐述和呈现生物学现象、特征、生命规律的表达形式，有利于学生体会学科间的联系，有利于培养和训练学生理科思维，提高学生的综合素质。