多分拣区FRP的GA&SS算法设计

陈彦如,单 翠,蒋阳升，魏朝恒，曾东红

(1.西南交通大学 经济管理学院， 四川 成都 610031；2.西南交通大学 交通运输与物流学院，四川 成都 610031)

多分拣区FRP的GA&SS算法设计

陈彦如1,单 翠1,蒋阳升2，魏朝恒1，曾东红2

(1.西南交通大学 经济管理学院， 四川 成都 610031；2.西南交通大学 交通运输与物流学院，四川 成都 610031)

考虑到遗传算法(GA)和分散搜索算法(SS)在求解大规模组合优化问题的优势，针对多分拣区的分拣存储指派决策(FRP)设计了GA&SS算法，对该算法的参数进行了敏感性分析。获得满意的参数组合后，将该算法与单纯形法的运行效果进行对比。结果表明：随着产品规模的增加，GA&SS算法较单纯形法有明显的时间优势。

管理工程；多分拣区；分拣存储指派决策；遗传算法；分散搜索

0 引 言

提高分拣效率、缩短分拣时间、降低分拣成本是提升配送中心竞争力的核心所在。众所周知，货物的储位分配对分拣成本的降低、分拣时间的减少有直接影响。为了降低分拣成本，许多配送中心设置了分拣区(Forward Area)和存储区(Reserve Area)。分拣区用于快速分拣，提高分拣效率。存储区用于大量存储、补货及未分配至分拣区产品的分拣。如何解决在有限的分拣区存放多少数量的何种产品，便形成了分拣存储指派决策(Forward-Reserve Problem，FRP)。

目前关于配送中心相关的研究成果已非常丰富。GU Jinxiang[1]较系统地分析了仓库设计问题，以仓库整个寿命周期内仓库总成本为优化目标。S.S.HERAGU等[2]综合考虑了分拣区空间大小和产品分配问题，以年分拣和存储成本最小为目标，建立了数学模型并给出启发式算法。J.C.H.PAN等[3]研究高层人至物分拣系统产品存储策略和分拣路径选择对订单分拣行程时间的影响。R.ACCORSI等[4]为提高仓储系统的设计和管理效率，设计了决策支持系统。D.B.DURDEVIC等[5]研究了配送中心内分拣区和存储区之间相互作用的各种影响因素，考虑服务水平不变的情况下，如何设计存储区与分拣区的位置来降低配送中心成本。HARWIN de Vries等[6]研究了基于3种不同补货优先级对分拣区补货时间的影响(基于存储需求、基于订单量及基于订单需求)。C.H.MOWREY等[7]分析了宽窄巷道的布置和分拣路径对分拣效率及成本的影响。周弘等[8]考虑了3层配送网络中产品分配和运输模式决策问题，以总费用最小和分拣中心负载的平衡为目标，建立了基于公共交货期的多目标物流配送优化模型。王凤珍[9]从订单产品种类的数量和需求相关性两个角度出发，考虑不同产品间的需求相关性，将多个成品仓库的产品进行重新分配。

上述文献为笔者提供了重要的研究基础，但这些研究大多集中在单一分拣区，对多分拣区的研究较少。而多分拣区由于灵活的配置及高效率的分拣，已经成为很多配送中心的选择。因此，多分拣区FRP的解决开始引起企业的关注。由于配送中心产品种类与数量众多，FRP算法的设计直接影响FRP的决策效率。笔者针对多分拣区FRP模型设计了GA&SS算法，并用算例验证了算法的有效性。

1 模型描述

多分拣区FRP主要解决什么产品应该以多少数量被分配至哪个分拣区的问题。由于分拣区的面积小于存储区，因而分拣区的分拣成本小于存储区的分拣成本。

决策变量：

则多分拣区模型描述如下：

(1)

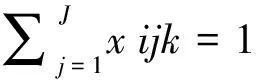
(2)

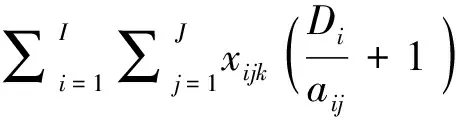
(3)

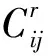
式(1)是模型的目标函数，以分拣区节省成本与建设成本及分拣区产品处理成本之差最大化为目标。约束条件式(2)保证了指派到分拣区的产品以一种存储方式存储到一个分拣区内。约束条件(3)表示指派到分拣区的产品存储空间不能超过分拣区容量。

2 算法设计

分散搜索( Scatter Search，简称SS)是Glover在20世纪70年代提出的一种启发式算法，它主要通过解的组合来进行寻优。由于SS算法的框架灵活，很容易和其他算法结合，更有效地完成解空间搜索。笔者尝试将SS与遗传算法(GA)相结合，用来解决多分拣区的产品存储组合优化问题。算法设计如下。

2.1 编 码

本阶段对可行解进行编码。考虑到将I种产品以J种存储方式放在K个分拣区，因此所设计的染色体总长度为I×J×K+I+K。染色体包括3个部分，第1部分长度为I×J×K，表示I种产品以J种方式在K个分拣区的存储方案。第2部分长度为I，表示I种产品的存储方式是否发生改变。第3部分长度为K，表示K个分拣区是否建立。

2.2 产生多样性初始解集

首先随机产生初始种群。由于某产品在某分拣区只能采取一种存储方式，需要保证在染色体的第1部分的每段基因体内代表某个分拣区的J个基因位中只能有1个基因位为“1”，该基因位随机产生。染色体的第2部分的基因由随机方式产生。染色体的第3部分的基因随机产生后，需进行判断，当第1部分染色体中某产品被分配到某分拣区后，第3部分染色体中该分拣区对应基因位才能为“1”。

在上述初始种群中采用Glover提出的多样性产生器选取50个多样性较好的解作为多样性初始解集。

2.3 构建初始参考集

参考集包含1组高质量的解和多样性的解。参考集在初始阶段被构建，包含从多样性初始解集中选出的5个高质量解和5个多样性解。高质量解通过以下适应度函数进行选取，即在初始解集中选择5个适应度最大的解作为参考集中的高质量解。

产生多样性解时，首先须评估解的多样性程度。可以考虑从当前种群中选取与其它解距离之和最小的解作为1个多样性的解，重复此过程直到产生5个多样性解为止，从而完成初始参考集的构建。

2.4 产生子集

子集产生方法是通过对参考集的操作产生一系列用于合并的解集。笔者采用了常用的子集产生方法，即生成参考集中所有的二元组，每个二元组作为一个子集，共(102-10)/2个子集。

2.5 交叉与变异合并子集产生新解

文中第1部分染色体采用两点交叉的方式，以保证产生的新个体为可行解。第2部分与第3部分采用单点交叉的方式。

变异操作是3部分分别进行变异，第1部分染色体在每个产品每个分拣区对应的基因段中搜寻值为“1”的基因，将其变为“0”，然后在其余的基因位中任选一位将其变成“1”，以保证变异后的个体为可行解。第2部分和第3部分染色体采取常规变异的模式，同时保证第1部分染色体与第3部分染色体的制约关系。

2.6 更新参考集

本算法采用静态更新方法，即在当前参考集和通过交叉变异产生的新解中选取5个目标函数值最优解和5个多样性最好解作为新参考集，具体操作同步骤3)。如果满足参考集未发生变化，则获得最佳方案，否则重复步骤4)～步骤5)。算法设计流程见图1。

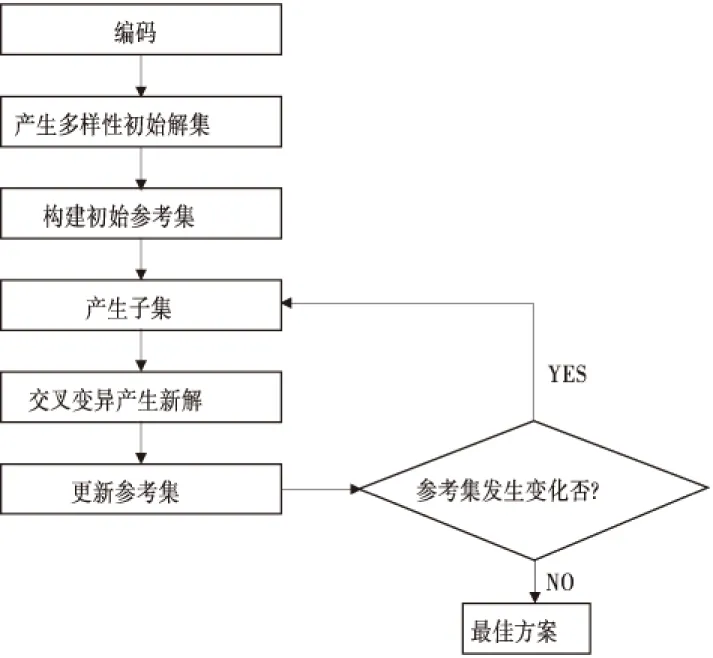
图1 算法设计流程Fig.1 Flow chart of proposed algorithm

3 算 例

某配送中心设有存储区与3个分拣区，分拣区容量分别为1 000，500，1 000。现有A，B，C，D4类产品，其需求分别为226，238，287，259。分拣区有两种存储方式。现假设3个分拣区单位空间的建设成本相同，均为10。产品成本如表1、表2。

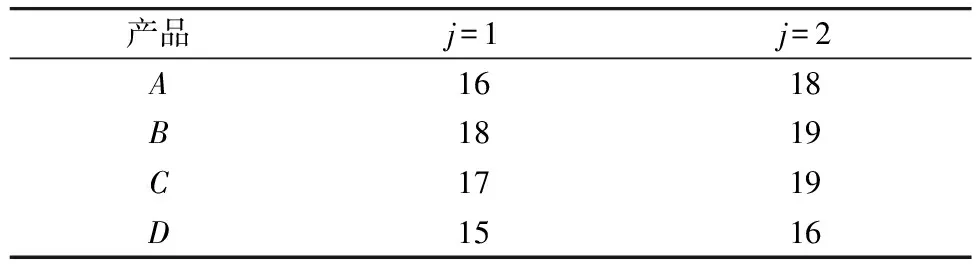
表1 产品在存储区的分拣成本

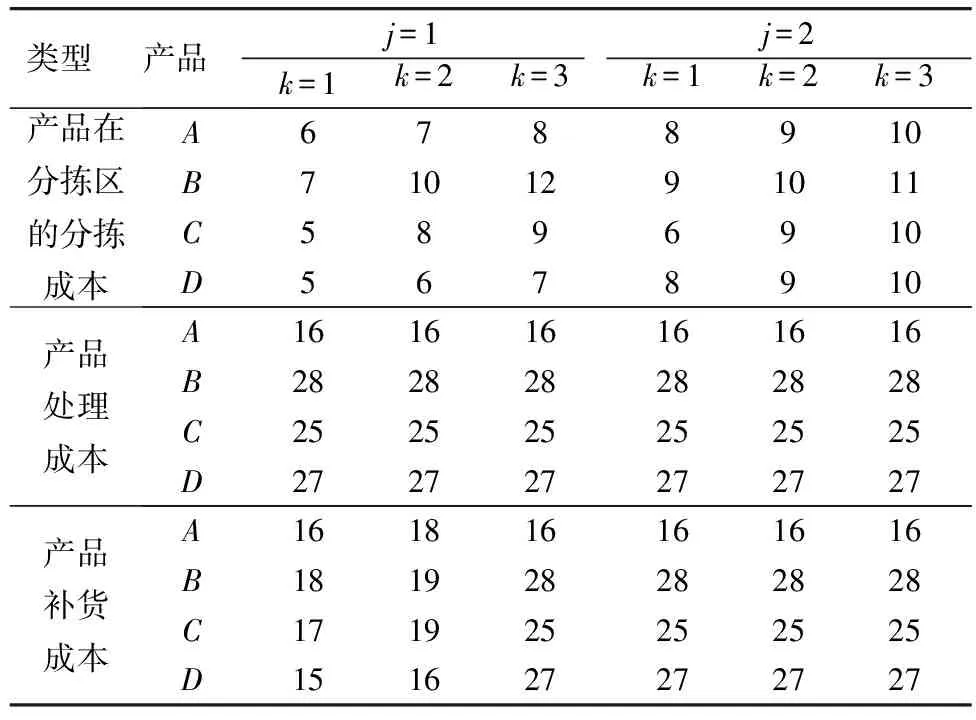
表2 产品在分拣区的分拣成本、处理成本及补货成本

由于算法参数选择对优化结果有一定的影响，笔者首先对不同参数进行测试，分别考虑种群规模为40，80；迭代次数为20，40；交叉率为0.5，0.6，0.8；变异率为0.1的参数组合进行测试，结果如图2。

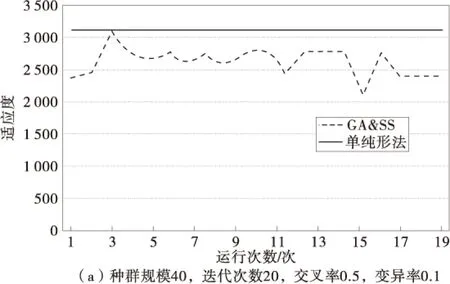
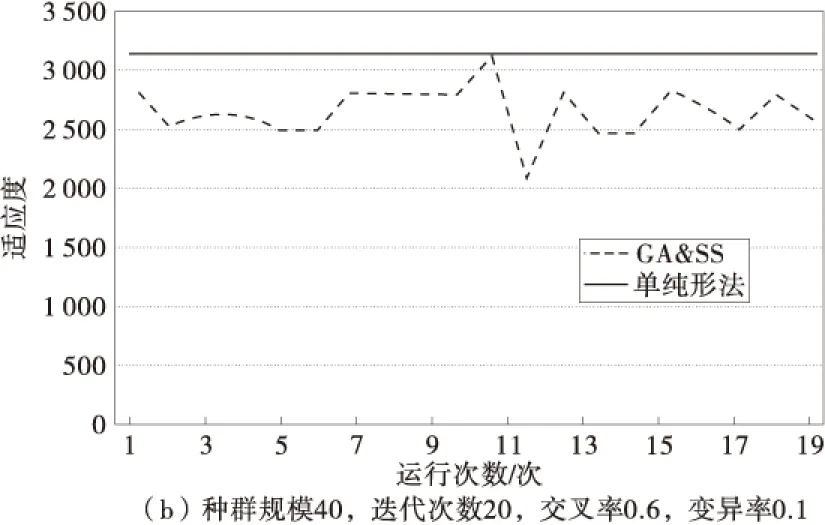
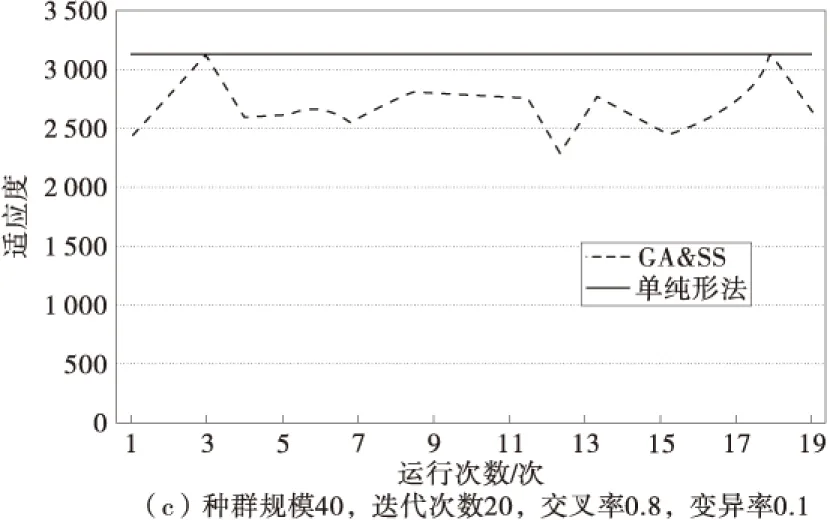
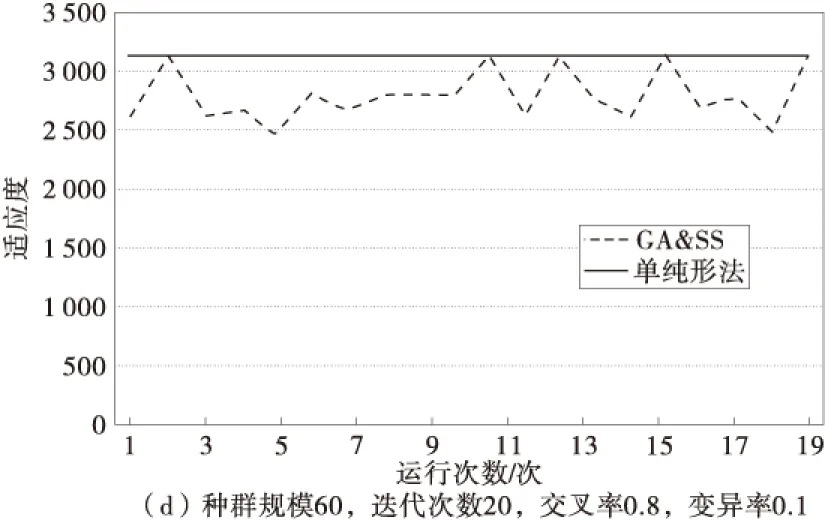
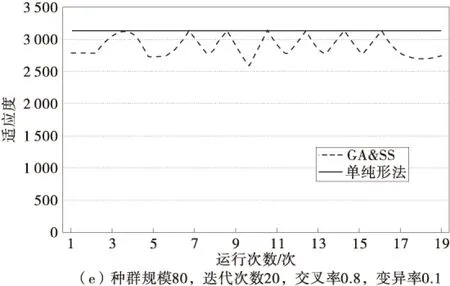
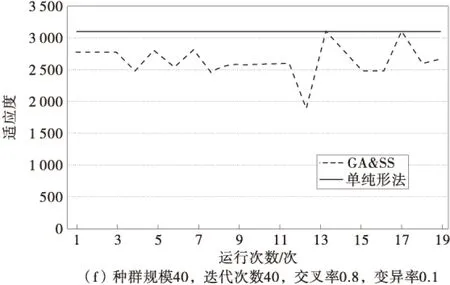
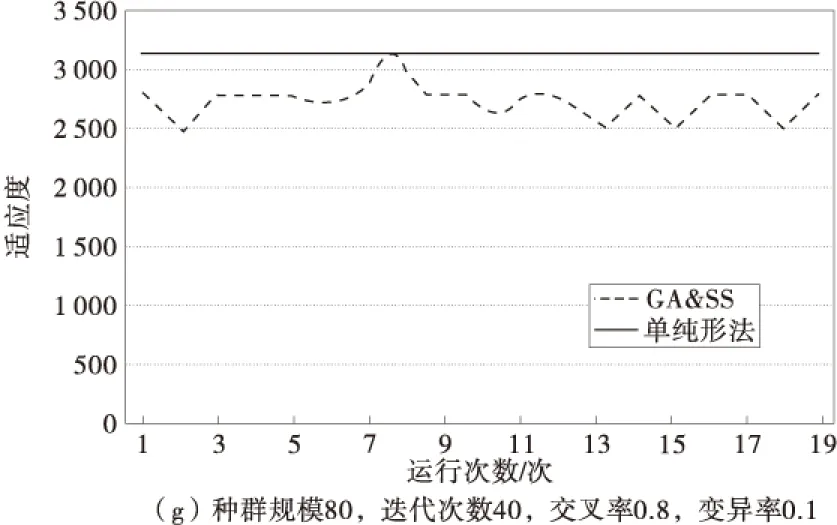
图2 不同参数组合下测试结果Fig.2 Test results with different parameter combinations

由图2可知：①在种群规模、迭代次数、变异率一定的情况下，交叉率为0.8时所得的结果比交叉率为0.5及0.6时更加平稳；②在迭代次数、交叉率、变异率一定的情况下，随着种群规模的不断扩大，满意解的质量及获得最优解的可能性逐渐增大，当种群规模为80时更容易达到最优解；③迭代次数由20增大到40时，对于运行结果(满意解的质量以及达到最优解的可能性)的影响不明显；④当迭代次数达到40时，随着种群规模的扩大，对于满意解的改进不理想，当迭代次数增大时，满意解的质量以及达到最优解的可能性反而更低。

因此，该问题最优的算法参数组合为种群规模80，迭代次数20，交叉率0.8，变异率0.1。在此参数组合下，将所设计的GA&SS与单纯形法从计算时间进行对比，如图3。

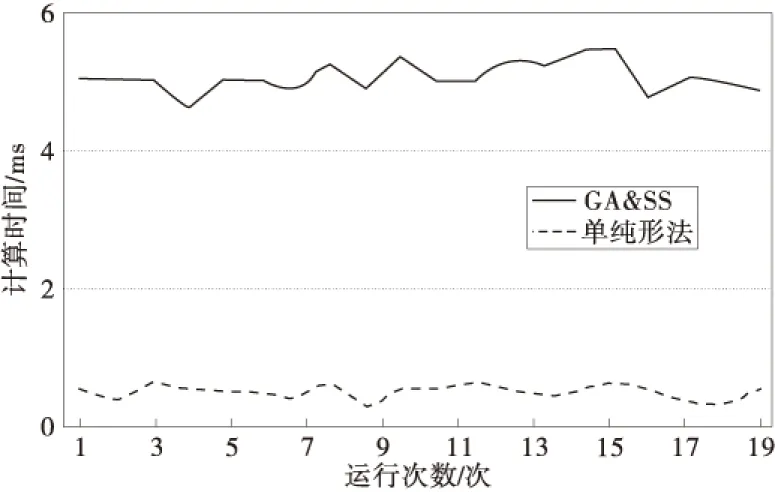
图3 4个产品两种算法的计算时间对比Fig.3 Comparison between the computation time of two algorithms for four products

当产品数增加到10时，两种算法的适应度与计算时间对比如图4(模型参数略)。

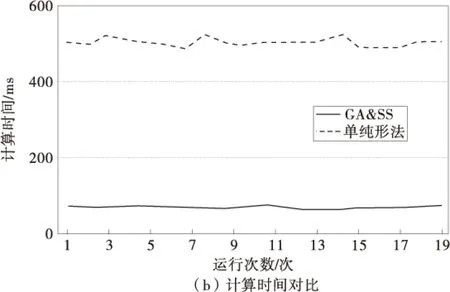
图4 10个产品的两种算法的对比Fig.4 Comparison between two algorithms for ten products

从结果可以看出，使用单纯形法可以找到最优解，但只适合数量规模小的产品，随着产品数目增加，该方法计算时间大幅上升，陷入“维度灾难”，而笔者所设计的算法，在产品规模增大后时间优势十分明显，可以在合理时间内得到较满意的方案。

4 结 语

多分拣区FRP是一类典型的组合优化问题，随着问题规模的增加，求解会变得越来越困难。考虑到遗传算法和分散搜索算法在求解大规模问题的优势，笔者针对多分拣区FRP设计了GA&SS算法。和单纯形法相比较，当产品规模较小时，该算法优势并不明显，但随着产品规模的增大，该算法时间优势越来越明显。

研究结果对大型配送中心多分拣区的运营方案的快速获取有一定参考价值，但研究依然存在一定的局限性，如选用更大规模的产品数对算法进行验证，以及考虑和多种算法进行比较，这将是笔者进一步研究的方向。

[1] GU Jinxiang.TheForwardReserveWarehouseSizingandDimensioningProblem[D].Georgia,USA:Georgia Institute of Technology,2005.

[2] HERAGU S S,DU L,MANTEL R J,et al.Mathematical model for warehouse design and product allocation [J].InternationalJournalofProductionResearch,2005,43(2):327-338.

[3] PAN J C H,WU M H,CHANG W L.A travel time estimation model for a high-level picker-to-part system with class-based storage policies [J].EuropeanJournalofOperationalResearch,2014,237(3):1054-1066.

[4] ACCORSI R,MANZINI R,MARANESI F.A decision-support system for the design and management of warehousing systems [J].ComputersinIndustry,2014,65(1):175-186.

[6] HARWIN de Vriesa,RUTH Carrasco-Gallegob,Taoying Farenhorst-Yuan,et al.Prioritizing replenishments of the piece picking area [J].EuropeanJournalofOperationalResearch,2014,236(1):126-134.

[7] MOWREY C H,PARIKH P J.Mixed-width aisle configurations for order picking in distribution centers [J].EuropeanJournalofOperationalResearch,2014,232(1):87-97.

[8] 周泓,孙江苏,谭小卫.多目标物流配送优化问题建模及其遗传算法设计[J].公路交通科技,2007,24(9):140-144. ZHOU Hong,SUN Jiangsu,TAN Xiaowei.Multi-objective optimization for logistic distribution and its genetic algorithm [J].JournalofHighwayandTransportationResearchandDevelopment,2007,24(9):140-144.

[9] 王凤珍.基于需求相关性的A企业产品库存分配策略[D].大连:大连海事大学,2013. WANG Fengzhen.AllocationStrategyofInventoryforEnterpriseABasedonDemandRelevance[D].Dalian:Dalian Maritime University,2013.

Developing GA&SS Based on FRP of Multiple Forward Areas

CHEN Yanru1, SHAN Cui1, JIANG Yangsheng2, WEI Chaoheng1, ZENG Donghong2

(1. School of Economics & Management, Southwest Jiaotong University, Chengdu 610031, Sichuan, P.R.China; 2. School of Transportation & Logistics, Southwest Jiaotong University, Chengdu 610031, Sichuan, P.R.China)

Based on the advantage of genetic algorithm (GA) and scatter search (SS) in solving large-scaled combinatorial optimization problems, an algorithm which combined GA and SS (GA&SS) was developed. Sensitivity analysis about parameters of GA&SS was also made to obtain optimal parameter combination. And the operation effect of the proposed algorithm was compared with that of the simplex method. The results show that the proposed GA&SS performs obviously better than simplex method does in computational time, with the increase of numbers of products.

management engineering; multiple forward areas; forward-reserve problem (FRP); genetic algorithm; scatter search

2014-05-07；

2014-09-26

四川省科技支撑计划项目(2012GZ0063)； 中央高校基本科研业务费专项资金资助项目(2682013CX074)

陈彦如(1974—),女,内蒙古包头人，副教授，主要从事物流与供应链优化方面的研究。E-mail: chenyanru@163.com。

10.3969/j.issn.1674-0696.2016.01.23

F253.4

A

1674-0696(2016)01-117-05