自适应事件驱动下马尔科夫跳变系统的状态估计

祁　琼

(南京财经大学 应用数学学院，江苏 南京 210046)



自适应事件驱动下马尔科夫跳变系统的状态估计

祁琼

(南京财经大学 应用数学学院，江苏 南京 210046)

摘要：研究了具有时变时滞的马氏跳跃系统的状态估计问题.为通过设置状态输出估计器使系统指数稳定，提出了一种自适应的事件触发通信方案.此方案的特点是，采样数据是否应该被发送由当前采样数据和最新传输数据与其之间的误差决定，它可以自适应地调整事件触发通信阈值，在确保所需控制性能的前提下减少信息通信负担.基于Lyapunov-Krasovskii泛函方法，通过求解线性矩阵不等式实现了对马尔科夫的状态估计.利用数据实例探讨了自适应事件触发的有效性.

关键词：马尔科夫系统；自适应事件触发；状态估计

近年来，马尔科夫跳跃系统因同时包含了连续的系统状态和跳变的结构而被广泛应用于许多工程领域,现阶段已有很多重要的成果[1-3].在许多应用中，如信号处理、控制工程等，只有部分信息可以从网络输出，因此，通过利用网络的有效输出量来估计系统状态，进而利用估计的状态来达到一定的设计目标，具有重要意义.近年来，基于事件触发机制的状态估计也得到了广泛关注[4-5].

文献[6]研究了一类新的离散时间神经网络及马尔科夫跳跃参数和模式相关的混合时间延迟的状态估计问题，其离散和分布式延迟是模式依赖的.值得注意的是，以往的研究大多是在预先指定的时间间隔采样，这被称为时间触发采样，该抽样方法可能会导致一个固有的周期性传输，并产生许多无用的消息，如果采样信号相比以前的采样没有显著改变时间触发采样则依然传输数据，这导致了通信资源的浪费.最近，事件触发的方案提供了一种有效的方法，其主要特征是对该信号进行周期采样，只有一些系统状态或输出测量超过阈值才被传输.与周期采样法相比，事件触发机制能减少通信的负担，也能保持理想的连续状态反馈系统的理想性能，如稳定性和收敛性.对事件触发机制的利用可以在许多文献中找到.本文在事件触发机制的基础上，通过调节事件触发阈值动态调节事件触发.本文的主要贡献有如下2点.

1)与时间触发周期通信方案相比较，提出了自适应事件触发方案.该通信方案只取决于采样时刻与当前采样时刻和前一传输状态之间的误差.因此，通过网络传输的状态信号的数目可能会明显降低.

2)通过利用Matlab中的LMI工具箱很容易求解线性矩阵不等式，其结果不仅依赖触发参数、采样周期，还依赖延迟的大小.

1问题描述

考虑一带有时滞的马尔科夫跳变系统：

(1)

其中x(t)∈Rn为状态向量，y(t)∈Rn为输出向量.{θt}是右连续且在有限集S={1,2,…,N}中的连续马尔科夫过程，马尔科夫跳转移概率为：

在式(1)中，时滞τ(t)是随时间变化的连续函数，满足以下条件：

其中τm,τM是通信时滞的下界和上界.

本节中，测量输出在进入估计器之前被采样，根据抽样技术，实际输出可被描述为：

(2)

样本数据y(tk+j)不满足以下的不等式则触发：

[y(tk+j)-y(tk)]TW[y(tk+j)-y(tk)]<σ(tk+j)yT(tk+j)Wy(tk+j)

(3)

其中σ(0)∈[0,1]是σ(t)的初始条件，σ(t)∈[σm,σM],ρ是一个非负常数.

(4)

将式(4)代入式(3)中得：

[x(tk+j)-x(tk)]TCT(θt)WC(θt)[x(tK+j)-x(tk)]<σ(tk+j)xT(tK+j)CT(θt)WC(θt)x(tk+j)

(5)

为方便起见，参考文献[7]，式(5)可写成：

(6)

(7)

(8)

(9)

其中:

2主要结论

本节中，将对马尔科夫跳跃系统设计自适应事件触发的状态估计器.式(9)可写为：

(10)

其中ξ(t)=

定理1假设式(5)成立，若对给定的估计增益矩阵K，式(10)均方意义上指数稳定的条件如下：存在一些适当维数的正定矩阵Pi>0,Q0>0,Q1>0,Q2i>0,Q3>0,Q4>0,R1>0,R2>0,R3>0,Zi>0,Mi2>0,Mi4>0,Ni2>0,Ni5>0,Hi3>0,Hi6>0,Gi3>0,Gi6>0(i=1,2)满足:

(11)

证明考虑下面式(12)的李雅普诺夫泛函:

(12)

其中:

根据式(10),对式(12)求导可得：

(13)

根据积分可加性得：

(14)

参考文献[10]可知： [8]和Schur补可知，‖‖2,参考文献[9]可知式(10)指数稳定.

(15)

结合式(14)和式(15)，式(13)可化简得:

(16)

考虑自由权矩阵Mi,Ni,Hi,Gi,其中:

(17)

在定理1的分析结果基础上，状态估计增益很容易根据定理2求得.

定理2假设式(5)成立，若对给定的估计增益矩阵K，使式(10)指数稳定的条件如下：存在一些适当维数的正定矩阵，Pi>0,Vi,Qj=diag{Qj,Qj}>0(j=0,1,3,4),Q2i=diag{Q2i,Q2i}>0,Ri=diag{Ri,Ri}>0(i=1,2,3),Zi>0,Mi2=diag{Mi2,Mi2}>0,Mi4=diag{Mi4,Mi4}>0,

Ni2=diag{Ni2,Ni2}>0,Ni5=diag{Ni5,Ni5}>0,Hi3=diag{Hi3,Hi3}>0,Hi6=diag{Hi6,Hi6}>0,Gi3=diag{Gi3,Gi3}>0,Gi6=diag{Gi6,Gi6}>0(i=1,2),对给定的ε>0满足：

(18)

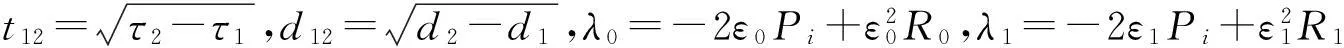
(19)

由于:

(20)

(21)

3数例仿真

考虑1个含有2个模态的马尔科夫跳跃系统(1)，系统参数如下.

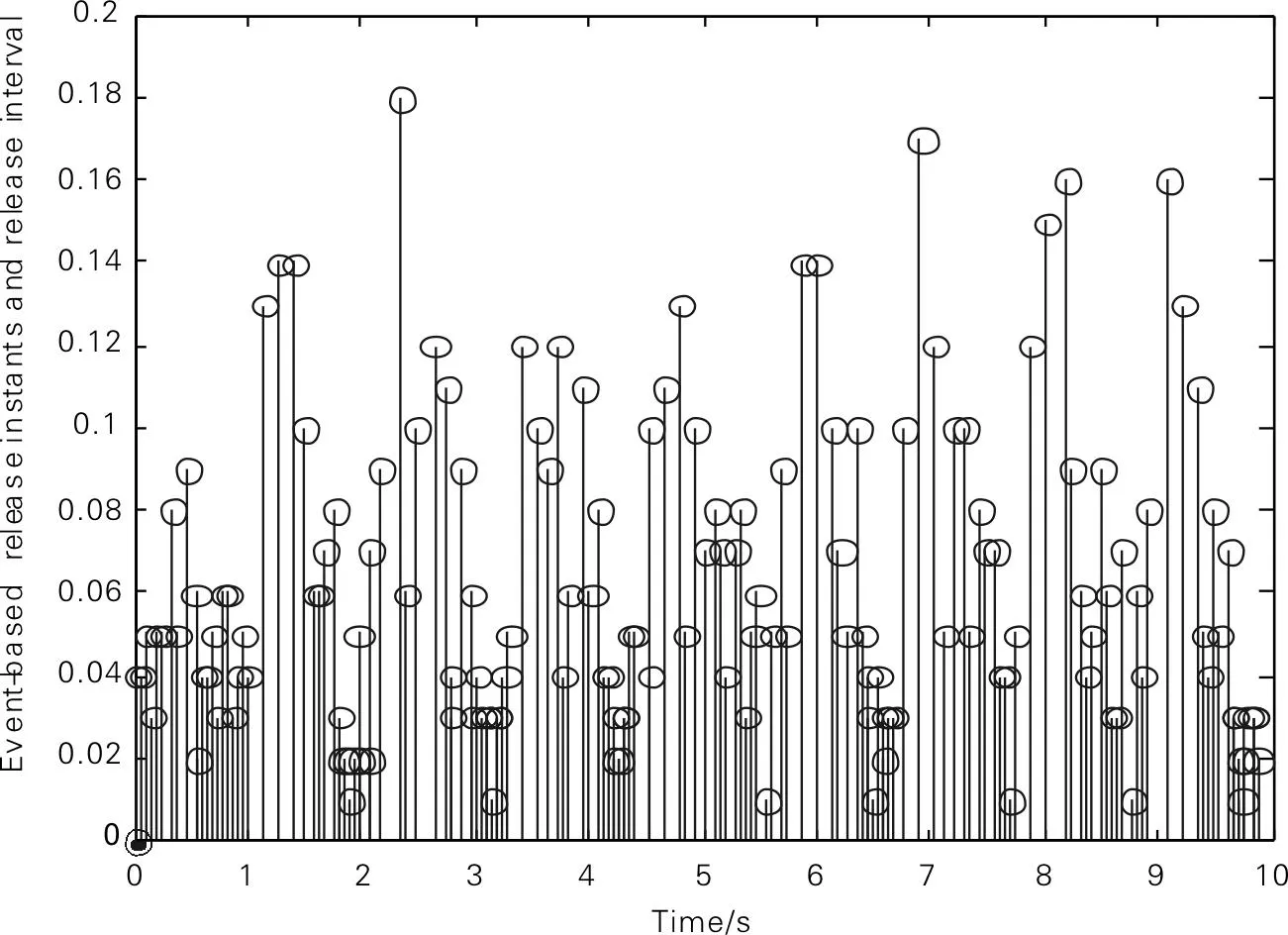
图1事件触发驱动下释放时刻和间隔图

图2自适应事件驱动下释放时刻和间隔图

由图1和图2可见自适应事件驱动触发点数量明显较少，触发参数的选取对触发点有明显影响，而自适应事件驱动触发参数不固定，只给定范围，能够在一定程度上削弱触发参数的影响力，避免触发点过少影响系统稳定，同时减少了一定的通信负载.参数d先在-1,0,1之间震荡，很快恒定为1之后σ就一直递增，最后达到所设定的σ最大值.系统状态很快达到稳定，而状态误差也很快趋向0.

4结论

本文研究了自适应事件触发驱动下马尔科夫跳跃系统状态估计问题，通过建立一个新的李雅普诺夫函数，利用矩阵不等式的凸性，得出使系统指数稳定的估计器增益，并利用数据实例仿真所得结果,由仿真结果可明显看出自适应时间触发能在保持系统性能的前提下降低触发参数的影响，同时在一定程度上减少了数据传输量.

[1]Y Kao,J Guo,C Wang,et al.Delay-dependent robust exponential stability of Markovian jumping reaction-diffusion Cohen-Grossberg neural networks with mixed delays[J].Journal of Franklin Institute,2012,349(6):1972-1988.

[2]S L Hu,D Yue,X P Xie,et al.Event-triggeredH∞stabilization for networked stochastic systems with multiplicative noise and network-induced delays[J].Information Sciences,2015,299:178-197.

[3]J L Liu,Z Gu ,S L Hu.H∞filtering for Markovian Jump Systems with time-varying delays[J].International Journal of Innovative Computing,Information and Control,2011,7(3):1299-1310.

[4]D R Ding,Z D Wang,B Shen,et al.Event-triggered distributed state estimation with packet dropouts through sensor networks[J].IET Control Theory and Applications,2015,9(13):1948-1955.

[5]Z W Jin,Y Y Hu,C Y Sun,et al.Event-triggered state fusion estimation for wireless sensor networks with feedback[C].Control Conference(CCC),2015 34th Chinese,2015:4610-4614.

[6]Y Liu,Z Wang,X Liu.State estimation for discrete-time Markovian jumping neural networks with mixed mode-dependent delays[J].Physics Letters A, 2008, 372(48):7147-7155.

[7]S Hu,D Yue.Event-triggered control design of linear networked systems with quantization[J].ISA Transactions,2015,51:4610-4614.

[8]X Wang,D Ma. Event-triggered control for continous-time switched systems[C].Control and Decision Conference,2015 27th Chinese,2015:1143-1148.

[9]C Peng,Y C Tian.Delay-dependent robust stability criteria for uncertain systems with interval time-varying delay[J].Journal of Computational and Applied Mathematics,2008,214(2):480-494.

(责任编辑高嵩)

State Estimation for Markovian Jump Systems Triggered by Adaptive State

QiQiong

(School of Applied Mathematics,Nanjing University of Finance and Economics,Nanjing Jiangsu 210046)

Abstract：This paper studies the state estimation problem for Markovian jump systems with time- varying delays.The main purpose is to obtain the system exponential stability by setting the state output estimator.Firstly, an adaptive event-triggering communication scheme is proposed.The feature of the scheme is that whether the sampling data should be transmitted or not is determined by error between the current sampling data the latest transmission data,At the same time,the threshold of the event-triggering mechanism is adaptively adjusted to reduce the burden of information communication under the premise of ensuring the needed control performance.Based on the Lyapunov-Krasovskii functional method,a state estimation of the Markovian systems can be achieved by solving the linear matrix inequalities (LMI).Finally,a numerical example is given to show the validity of the proposed adaptive event-triggering scheme.

Key words：Markovian systems;adaptive event-triggering scheme;state estimation

中图分类号：O231.1

文献标识码：A

文章编号：2095-4565(2016)02-0042-08

doi:10.3969/j.issn.2095-4565.2016.02.010

作者简介：祁琼，硕士。

收稿日期：2015-10-14