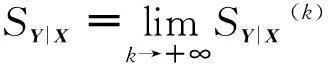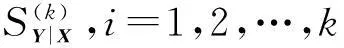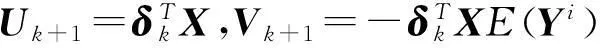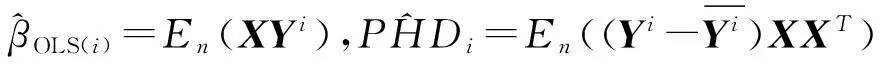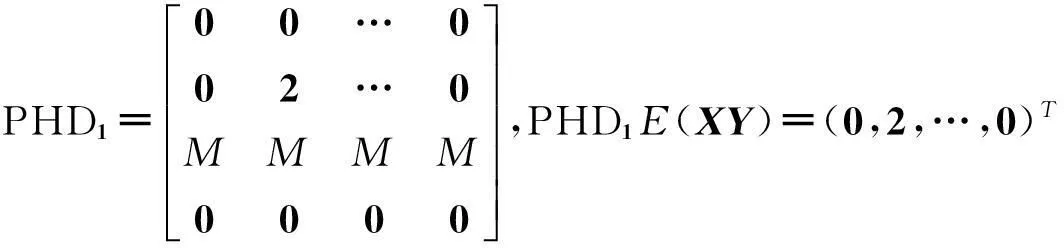中心K阶中心矩子空间的迭代海塞变换估计

甘胜进，游文杰

(福建师范大学福清分校电子与信息工程学院,中国 福清　350300)



中心K阶中心矩子空间的迭代海塞变换估计

甘胜进*，游文杰

(福建师范大学福清分校电子与信息工程学院,中国 福清350300)

摘要提出中心K阶条件矩降维子空间，指出与中心K阶中心矩子空间的关系，并给出迭代的海塞变换估计，该方法仅仅需要线性条件，综合了最小二乘和海塞主方向方法．

关键词降维;CKCMS;OLS;PHD;迭代海塞变换

在高维空间中进行统计建模，往往会碰到“维数灾难”(curse of dimensionality)问题，因此降维作为建模之前的数据预处理阶段，显得十分重要．常见的降维方法有主成分回归分析、偏最小二乘回归和投影寻踪等，主成分回归仅仅考虑了自变量之间的相关信息，忽略了与因变量之间的关系，而偏最小二乘虽然同时考虑自变量与因变量之间相关关系，但是仅仅局限于线性关系，没有考虑非线性关系，另外投影寻踪需要估计连接函数，超出数据预处理的范围．

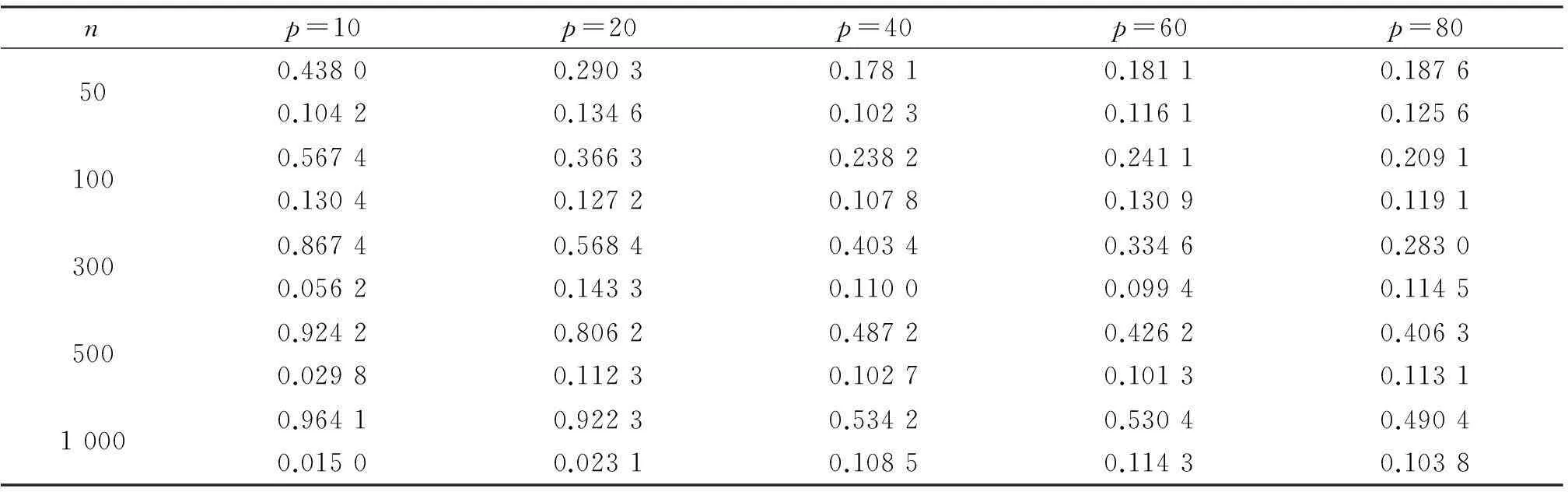
对于一维响应变量Y和p维解释变量X=(X1,X2,…,Xp),考虑它们之间的回归问题本质上是讨论在X给定条件下，Y的条件分布FY|X如何随X变化．Li(1991)[1]提出切片逆回归(sliced inverse regression,简称SIR)，即如果存在p×k(k

Y‖X|X⟺Y‖X|ηTX，

(1)

则FY|X(y|x)=FY|ηTX(y|ηTx)，Y对X条件分布是k维的，如果k远小于p，就达到了降维的目的，特别地，当k=1或2时，便可从可视化角度来分析Y与X之间的回归关系，由于Y‖X|ηTX⟺Y‖X|(ηB)TX,其中B为k阶可逆方阵，η与ηB所形成的子空间一样，所以关心的是span{η}，而不是η本身，并称span{η}为降维子空间．如果满足(1)的所有η的交集仍然满足(1)，则称之为中心降维子空间(central dimension reduction subspace,简称CS)，记为SY|X,rank(SY|X)称为结构维数.一般来说，在很弱条件下CS总是存在的.有时候感兴趣的是E(Y|X),Cook和Li(2002)[2]提出中心均值子空间，即：

Y‖E(Y|X)|ηTX.

(2)

类似CS，若所有满足(2)的集合的交集仍然满足(2)，称之为中心均值降维子空间(central mean dimension reduction subspace,简称CMS)，记为SE(Y|X)．估计降维子空间[3-4]的条件通常为：

(1)线性条件：E(X|ηTX)为ηTX线性函数，即E(X|ηTX)=PηX,∀η∈Rp，其中投影阵Pη=η(ηTη)-1ηT．

(2)常数方差 ：Var(X|ηTX)为非随机矩阵．

满足线性条件一般要求X是椭圆分布，满足常数方差条件的是多元正态分布.本文分三个部分，第二部分提出中心K阶条件矩降维子空间定义，并指出与中心K阶中心矩子空间的关系，第三部分为利用Cook和Li[5](2004)提出的迭代海塞变换方法来估计中心K阶条件矩子空间，最后部分给出实例模拟．

1中心K阶条件矩子空间

Yin和Cook(2002)[6]提出中心K阶中心矩子空间定义：

Y‖{M(1)(Y|X),…,M(k)(Y|X)}|ηTX,

(3)

定义1如果Y‖E(Yk|X)|ηTX成立，则称span{η}为K阶条件矩降维子空间,若span{η}仍然是K阶条件矩降维子空间，则称之为中心K阶条件矩降维子空间，记为SE(Yk|X)．显然SE(Yk|X)⊆SY|X，类似Cook和Li(2002),给出以下定理．

定理1以下3个命题相互等价

(i) Y‖E(Yk|X)|ηTX；

(ii)Cov[(Yk,E(Yk|X))|ηTX]=0；

(iii)E(Yk|X)是ηTX的函数.

证显然(i)⟹ (ii)，(iii) ⟹(i)，只需证明(ii) ⟹(iii)，由(ii)可知

E[YkE(Yk|X)|ηTX]=E(Yk|ηTX)E(E(Yk|X)|ηTX).

依据条件期望的平滑性，左边等于E[E(YkE(Yk|X)|X)|ηTX]=E[E2(Yk|X)|ηTX],右边第一项E(Yk|ηTX)=E(E(Yk|X)|ηTX).故右边等于E2(E(Yk|X)|ηTX)，所以Var(E(Yk|X)|ηTX)=0，表明在ηTX给定条件下，E(Yk|X)是常数，故(iii)成立．(iii)表明E(Yk|X)=E(Yk|ηTX).

证对于任意的k≥2

(4)

由(3)可知Y‖E(Y|X)|ηTX，故Y‖Ei(Y|X)|ηTX，

由于Y‖{M(1)(Y|X),…,M(k)(Y|X)}|ηTX，故Y‖{E(Y|X),…,E(Yk|X)}|ηTX

2CKCMS的迭代海塞变换估计

Yin和Cook(2002)在线性条件下给出最小二乘估：

βOLS=(E(YX),E(Y2X),…,E(YkX)).

(5)

Yin和Cook(2006)[7]在线性条件和常数方差条件下给出高阶海塞主方向估计：

Mphdk=(E[(Y-E(Y)XXT],E[(Y2-E(Y2)XXT],…,E[(Yk-E(Yk)XXT]).

(6)

式(5)虽然条件弱，但是没有估计出CKCMS中更多的方向，式(6)相对于(5)似乎得到更多估计方向，但是需要条件较为苛刻．本节提出一种新的估计方法，只需要在线性条件下，以最小二乘为种子向量，最小二乘与高阶海塞矩阵[8-11]不断结合产生新的方向，其理论依据如下．

定理3假设E(X|ηTX)为ηTX线性函数，U,V均为关于ηTX可测的函数，即U=U(ηTX),V=V(ηTX),则E((UYi+V)X)∈span(η),i=1,2,…k.

证

E[(UYi+V)X]=E[(E(UYi|X)+E(V|X))X]=E[(UE(Yi|X)+V)X]=

E[(UE(Yi|ηTX)+V)X]=E[(UE(Yi|ηTX)+V)E(X|ηTX)]=E[E(UYi+V)E(X|ηTX)]=

PηE[(UYi+V)X]∈span(η)

选取适当的U,V可以得到迭代的海塞变换估计:

推论1取U0=(E(YiX))TX,V0=-(E(YiX))TXE(Yi)，则

证在线性条件下，最小二乘估计E(YiX)∈SE(Yi|X)

U1=δ1TX,V1=-δ1TXE(Yi)代入定理3.1中得到

δk+1=E[(UkYi+Vk)X]=[E((Yi-E(Yi))XXT)]k+1E(YiX)，证毕．

实际当中span{E(YiX),[E((Yi-E(Yi))XXT)]jE(YiX),j=1,2,…,n,…}的维数不可能是无限的，最多是p，下面定理给出迭代停止条件．

定理4对于p维列向量序列:β,Aβ,A2β,…,Anβ,…,如果某个k,β,Aβ,…,Akβ线性相关，则β,Aβ,…,Anβ,n≥k线性相关．

证不失一般性，假设β,Aβ,…,Ak-1β线性无关，而β,Aβ,…,Akβ线性相关，则Akβ可由β,Aβ,…,Ak-1β线性表示，Ak+1β=A(Akβ),所以Ak+1β可由β,Aβ,…,Ak-1β线性表示，以此类推可得Anβ可由β,Aβ,…,Ak-1β线性表示，证毕．

推论1、定理4给出迭代海塞变换估计方法，具体步骤如下：

(a) 计算βOLS(i)=E(YiX),PHDi=E((Yi-E(Yi))XXT),i=1,2,…,k

(b) 计算(PHDi)jβOLS(i),j≤p-1

(c) 判定βOLS(i),PHDiβOLS(i),…,(PHDi)jβOLS(i)是否线性相关，若无关，则j=j+1重复(b),若相关，则停止迭代，span{βOLS(i),PHDiβOLS(i),…,(PHDi)j-1βOLS(i)}=ηi

(d) 最后得到CKCMS的迭代海塞变换估计span{η1,η2,…,ηk}

3模拟研究

表1为针对维数p和样本容量n在100次重复下迭代海塞变换估计模拟结果，其中每个格子里第一个数为均值，第二个数为标准差．

表1　迭代海塞变换估计方向与真实方向接近程度的均值与标准差

从表1可以看出：维数相同情况下，迭代海塞变换估计方向与真实方向接近程度的均值越来越大，标准差越来越小，表明样本容量越大，估计的效果越好，说明估计具有相合性；样本容量相同情况下，维数越高，均值越小，而标准差变化不大，表明维数越高，该方法估计的效果越差，但稳定性较好．因此迭代海塞变换收敛速度依赖样本容量和解释变量的维数．图1和图2为100次重复下，维数p=8,样本容量分别为300和500时，迭代海塞变换估计与现常见方法如切片逆回归(切片数量为10)、最小二乘相比较．

图1　　　　样本容量为300时，IHT、SIR、OLS与真实方向接近　　 　　图2　　　　样本容量为500时，IHT、SIR、OLS与真实方向接　　　程度的箱线图　　　近程度的箱线图Fig.1　　　　Boxplots of distances between directions estimated by IHT, SIR, 　　Fig.2　　　　Boxplots of distances between directions estimated by IHT, SIR, 　　　OLS respectively with real directions under sample size 300　　　OLS respectively with real directions under sample size 500

通过比较发现：最小二乘估计非常稳定，但是估计的效果远远不及前两者，当样本容量变大时，与其他两种方法估计效果的差距越来越大,一个很重要的原因是最小二乘只能估计降维子空间中的一个方向；切片逆回归性能对切片数量较为敏感，如何选择切片数量至今是个公开的难题，并且当回归函数是偶函数时，该方法失效；相比之下迭代海塞变换随着样本容量增大在估计效果与稳定性方面越来越好．

致谢感谢审稿人的细致和编辑提出的有益建议！

参考文献：

[1]LI K C. Sliced inverse regression for dimension reduction[J]. J Am Stat Assoc,1991,86(414):316-327.

[2]COOK R D, LI B. Dimension reduction for conditional mean in regression[J].Ann Stat, 2002,30(2):455-474.

[3]COOK R D, LI L X. Dimension reduction in regressions with exponential family predictors[J].J Comput Graph Stat, 2009,18(3).

[4]PENG Z, YU Z. An integral transform method for estimating the central mean and central subspaces[J]. J Multiv Anal, 2010,101:271-290.

[5]COOK R D, LI B. Determing the dimension of iterative Hessian transformation[J]. Ann Stat,2004,32(6):2501-2531.

[6]YIN X R, COOK R D. Dimension reduction for the conditional kth moment in regression[J].J Statist Soc B, 2002,64:159-175.

[7]YIN X Y, COOK R D. Dimension reduction via marginal high moments in regression[J].Stat Prob Lett, 2006,76:393-400.

[8]LI K C. On principal hessian directions for data visualization and dimension reduction :another application of stein’s lemma[J].J Am Stat Assoc,1992,87:420.

[9]COOK R D. Principal hessian directions revisited[J]. J Am Stat Assoc, 1998,93:441.

[10]LUE H H. On principal Hessian directions for multivariate response regressions[J]. Comput Stat, 2010,25:619-632.

[11]ZHOU Y, DONG Y X, FANG Y. Marginal coordinate tests for central mean subspace with principal Hessian directions[J]. Chin J Appl Proba Stat,2010,26(5).

[12]ZHU L P, ZHU L X, WEN S Q. On dimension reduction in regression with multivariate responses[J]. Stat Sin, 2010,20:1291-1307.

[13]RAPHAEL C, STEPHANE G, JEROME S. A new sliced inverse regression method for multivariate response[J]. Comput Stat Data Anal，2014,77:285-299.

(编辑HWJ)

Iterative Hessian Transformation Estimation of CentralKthConditional Moment Subspace

GANSheng-jin*,YOUWen-jie

(School of Electronical and Information Engineering, Fuqing Branch of Fujian Normal University, Fuqing 350300, China)

AbstractThis paper defines the central Kthmoment subspace, and has derived its relationship with CKCMS. In addition, iterative Hessian transformation estimation has been proposed, which is a combination of ordinary least square estimation and principal Hessian directions applied only to the linear condition.

Key wordsdimension reduction; CKCMS; OLS; PHD; IHT

中图分类号O213

文献标识码A

文章编号1000-2537(2016)02-0090-05

*通讯作者,E-mail：ganshengjin2001@163.com

基金项目：国家自然科学基金资助项目(61473329)；福建省自然科学基金资助项目(2015J01009)

收稿日期：2015-03-23

DOI:10.7612/j.issn.1000-2537.2016.02.015